基于模型参数化的地震波走时与射线路径计算

孙建国，李懿龙，孙章庆，苗 贺

吉林大学地球探测科学与技术学院，长春 130026

0 引言

模型参数化是对地震波传播介质的定量化描述[1]，影响着地震的正演和反演等各个方面。根据实际问题的需要，模型参数化的过程需要精心地设计安排。不恰当的参数化方式或是过于简化的方式都会降低探测地球非均匀性地质结构的能力，使得一些有意义的信息丢失掉；而对于复杂的模型参数化设计又反而会使反演的不确定性剧烈增加，引入一些不真实的地下信息[2]。

地震波走时计算及射线路径追踪被广泛应用于地震层析成像[3]、地震波场正演、Kirchhoff偏移[4]、走时反演、模型计算等方面中，在理论研究和实际生产方面都具有重要意义，因此它们计算的有效性和精确性直接影响到上述各方面研究的效率和精度。计算地震波走时的方法主要分为两大类：射线追踪类和波前追踪类。射线追踪类基本理论基础是费马原理，主要包括试射法[5]、弯曲法[6]、最短路径射线追踪法[7]、插值法[8]、辛几何算法[9-10]等；波前追踪类方法主要包括基于运动学射线追踪系统的波前构建法[11-12]和基于惠更斯原理、解程函方程的有限差分方法[13-14]。本文走时计算采用有限差分法中的波前快速推进(FMM)法。该方法由Sethian等[15]提出，具有灵活性强、计算速度快、对任何复杂速度场都具有无条件稳定性的优点。差分格式采用迎风有限差分格式。目前射线路径追踪最具代表性的3种方法为：有限差分法、最短路径法和走时线性插值(LTI)法[16]。本文采用的是最大旅行时梯度射线追踪(MGT)法，其核心思想与LTI一样，都是基于费马原理，但MGT更加精确高效。

本文的研究目的是在射线追踪研究中加入模型参数化方法，进而提高射线追踪中走时计算及路径追踪的精度。模型参数化采用最小二乘参数化法，分别参数化速度模型和走时模型。以速度模型为例，先将离散的地震速度模型参数化，转换成离散的参数模型，进而得到连续地震速度模型，将其应用于地震波走时计算。通过均匀梯度速度模型进行地震波走时计算误差分析，进而研究模型参数化对地震波走时计算的影响。

1 FMM走时计算和MTG路径追踪

1.1 FMM基本理论

射线追踪是基于对波动方程的高频近似，其近似方程为程函方程：

|t|=s。

(1)

式中：t为地震波走时；s为传播介质的慢度。它们都是空间位置的函数。

FMM是基于求解程函方程来获得地震波走时的，计算得到的是初至走时，因而可以看成是追踪一个沿给定模型速度的法线方向扩展演化的二维曲线或三维曲面，即追踪波前。

构建迎风差分格式来求解程函方程：

(2)

(3)

式中：Δx和Δz分别表示横向和纵向网格间距。

1.2 MGT基本理论

MGT法求取射线路径的核心思想是，射线的传播路径是沿着旅行时最小的方向，即走时场的梯度方向传播的。该方法在计算中是沿着走时场梯度的负方向逐步检索次级源点，最终走到地震源点，即能够确定出地震波在地下介质中的射线追踪路径。

2 参数化方法

模型参数化过程是将介质参数投影到某一函数空间，并基于该空间的基函数进行展开[17]。本文采用的是最小二乘参数化法。

最小二乘法是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。这种求误差平方和的方式可以避免正负误差相抵，而且便于数学处理。由于我们所接触的模型都是离散的点阵模型，因此使用最小二乘法进行拟合，可以将其转换成连续的函数形式。在函数的基础上进行网格加密和求导等操作更为简单、合理。

本文采用的函数为多项式函数：

pn(x)=anxn+…+a2x2+a1x+a0。

(4)

速度模型的一般形式为v(xi,yi)(i=1,2,…,m)，其中(xi,yi)为速度模型中任意一点，m为横纵方向模型点数。通过确定多项式的一系列系数aj(j=0,1,…,n)，使得各点函数值与实际值的偏差平方和M达到最小。数学形式为使

(5)

达到最小。由于M非负且为a0,a1,…,an的二次多项式，所以M(a0,a1,…,an)必有最小值。因此令

(6)

将地震模型v(xi,yi)带入到式(6)中得到方程组：

sja0+sj+1a1+…+sj+nan=uj(j=0,1,…,n)。

(7)

(8)

由式(8)即可很方便地求取多项式系数aj，从而得到模型参数化函数。

3 方法实现及精度分析

本文采用最小二乘参数化法进行模型参数化，对于走时计算及射线路径追踪分别对速度模型和走时模型进行模型参数化，使得FMM的走时计算精度和MGT的射线路径计算精度都得到明显提高。下面将分别阐述模型参数化在走时计算及射线路径追踪中的作用。

3.1 速度模型参数化

FMM是一种理论基础好、算法实现优越性明显的方法。采用差分算子来近似微分算子，在近似中会省略掉网格间距的n阶无限小量，因此导致网格间距成为走时计算精度的主要影响因素。采用模型参数化后的模型进行网格加密，缩小网格间距，从而提高计算精度。

在刚开始的研究中采用全列数据进行多项式拟合，发现误差极大；经过分析研究后采取按列再按点的方式进行细化，每五点采用最小二乘多项式拟合一次，得到速度模型所对应的参数数组数据，化速度模型为参数模型，使得模型不再是离散点数据模型而是参数化连续速度模型。将此模型应用到地震波走时计算上，可以极大地提高计算精度。

下面应用均匀的速度梯度模型进行精度分析，网格大小为40×40，网格间距为40 m，震源设置在(0, 20)。加密后模型网格为400×400，网格间距减小到4 m，震源保持不变。

图1a为初始模型FMM地震波走时计算值与解析值的逼近程度，图1b为模型参数化之后加密重新采样的计算值与解析值的逼近程度，从中可以明显看出，经过模型参数化后的地震波走时值与解析值逼近效果比原模型效果好。图2所示为模型参数化前后走时的相对误差，表1为相对误差与模型参数化程度的关系，从中可以很明显地看出：相对误差由原来的10-2数量级降到10-3数量级，模型参数化可以极大地提高地震波走时计算的精度；并且随着模型参数化加密程度的提高，地震波走时精度也随之提高。因此，我们的方法对于提高地震波走时计算精度是有用的。

图1 模型参数化前(a)后(b)计算值与解析值的逼近程度Fig.1 Degree of approximation between the calculated and analytic values before (a) and after (b) model parameterization

图2 模型参数化加密前(a)后(b)误差对比Fig.2 Model parametric encryption before (a) and after (b) error contrast

Table1Comparisonoftraveltimerelativeerrorsbeforeandaftermodelparametricencryption

网格大小走时相对误差40×40(原模型)0．026980×80(加密1倍)0．0188400×400(加密10倍)0．0083

3.2 走时模型参数化

对于MGT法，由于初始模型都是离散的，因此导致由离散走时场而获得的旅行时梯度存在很大的不稳定性，路径计算的误差较大。在此情况下，应用本文所提出的模型参数化方法，将对其起到根本性的作用，提高计算精度。将离散走时场转化成连续走时场，进而可以求取任意走时点的时间梯度，使得时间梯度的求取更为合理、稳定，提高射线路径追踪的精度。本文对走时场所采用Chebyshev多项式进行最小二乘参数化。在二维走时场上采取九点拟合，获得4个Chebyshev多项式系数，进而将离散的走时场转化成连续的时间场函数。依然应用均匀速度梯度模型进行精度分析，并将其与离散模型进行对比，离散模型的时间场梯度由中心差分法求得。模型网格大小为100×100，网格间距为4 m，震源设置在(0, 200)处。

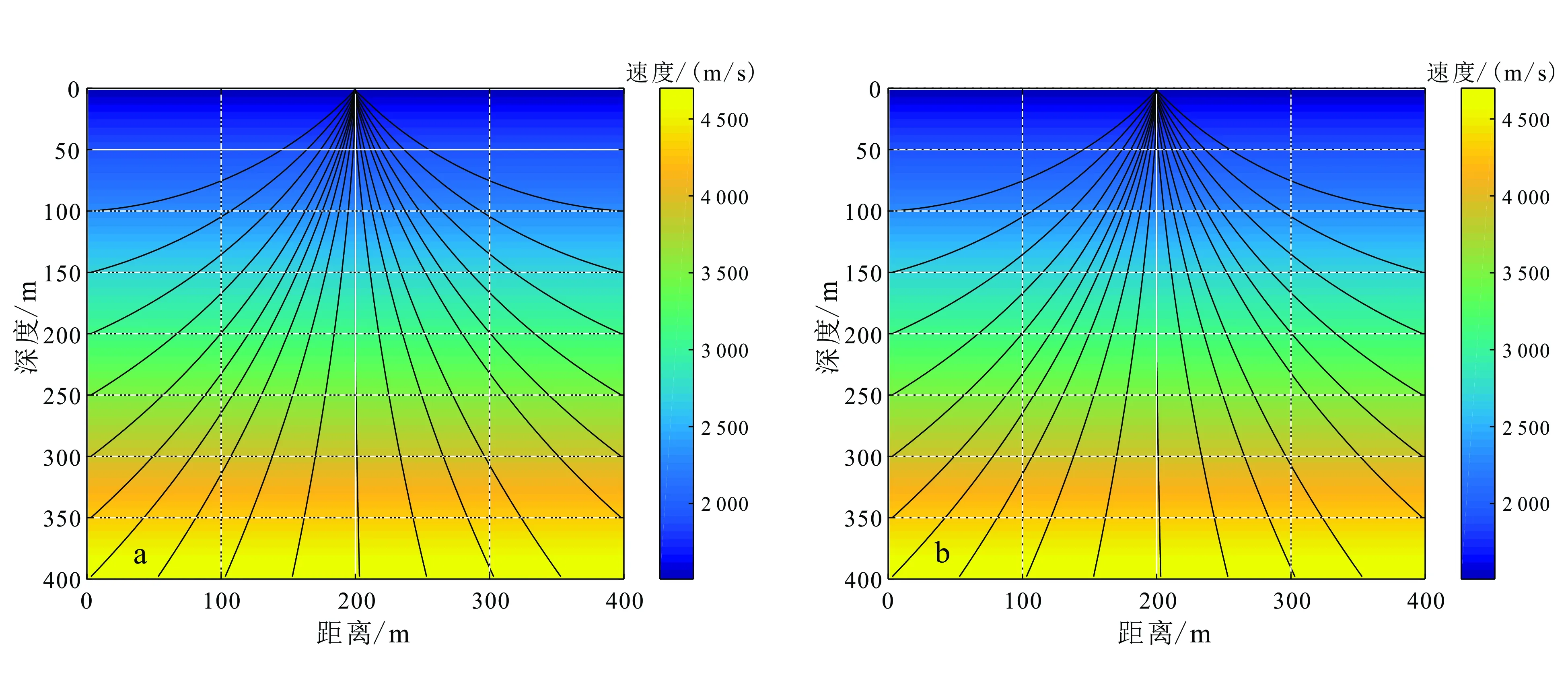
图3 离散模型(a)与参数化模型(b)射线路径对比Fig.3 Ray path contrast between discrete model (a) and parametric model (b)

图4 参数化前后射线路径相对误差对比图Fig.4 Comparison of relative errors of ray paths before and after parameterization

图3为模型参数化前后梯度速度模型的射线追踪路径图，图4为模型参数化与离散模型的射线路径精度对比图，从中可以看出模型参数化对于追踪射线路径的精度有明显改善，平均精度提高了14.33%。

4 计算实例

下面给出两组经典地震速度模型——Marmousi模型和Sigsbee 2A模型的走时计算及射线追踪实例，以验证模型参数化法在地震波走时计算及在射线路径追踪计算方面的确切可行性。

图5为Marmousi模型参数化前后的地震波走时对比图，该速度模型包含有极为复杂的地质构造，为50×50，网格间距为40 m，震源取在(1, 35)，参数化后重新加密采样网格大小为500×500。对比参数化前后的计算结果可以看出，在模型较深的复杂介质中，模型参数化处理之后的等时线在局部明显被细化，地震波传播显得更为合理。图6为Sigsbee 2A模型，网格大小为600×600，网格间距为4 m,参数处理之后为6 000×6 000，震源取在(1,1)。对比图6中模型参数化前后的计算结果依然可以看出，在地下异常高速体中地震波走时的等时线在模型参数化后显得更为细致。图5、图6的计算结果表明，本文提出的模型参数化法切实可行，适用于任意的复杂速度模型。

图7为走时模型参数化在射线路径追踪中的应用。图7a为Marmousi模型，网格大小为500×500，网格间距为4 m；图7b为Sigsbee 2A模型，网格大小为600×600，网格间距为4 m。图7中模型的有些区域没有射线穿过，那是由于本文所计算的是最小走时射线路径，所以射线会尽量选择高速层穿越，进而达到走时最小的目的。图7从射线追踪计算路径的角度证明了本文的模型参数化方法对于地下复杂介质的有效性。

图5 二维Marmousi模型参数化前(a)后(b)等时线对比Fig.5 Two dimensional Marmousi model parameterization before (a)and after (b) isochronous correlation

图6 二维Sigsbee 2A模型参数化前(a)后(b)等时线对比Fig.6 Two dimensional Sigsbee2A model parameterization before (a)after (b) isochronous correlation

a. Marmousi模型；b. Sigsbee 2A模型。图7 走时模型参数化在追踪射线路径中的应用Fig.7 Application of traveltime model parameterization in tracking ray paths

5 结论

1)模型参数化是对地震波传播介质的定量化描述，影响着地震处理的各个过程。对速度模型进行恰当的参数化处理，可以提高地震波走时计算的精度。通过对走时模型的参数化处理，使得求取走时场的梯度更为合理、稳定，相对于离散模型，最终获得的射线路径精度更高。

2)模型参数化具有普遍适用性，且无论是速度模型还是走时模型等都可以很好地参数化。并且，本文方法对于任何复杂走时计算均适用，且具有很好的稳定性。

[1] 李贞,郭飚,刘启元，等. 地震层析成像中模型参数化研究进展[J]. 地球物理学进展,2015, 30(4): 1616-1624.

Li Zhen, Guo Biao, Liu Qiyuan, et al. Parameterization in Seismic Tomography[J]. Progress in Geophysics, 2015， 30(4): 1616-1624.

[2] Thurber C H, Aki K. Three-Dimensional Seismic Ima-ging[J]. Annual Review of Earth and Planetary Sciences, 1987，15(1): 115-139.

[3] Dziewonski A M, Woodhouse J H. Global Images of the Earth’s Interior[J]. Science, 1987, 236: 37-48.

[4] Sena A G, Toksoz M N. Kirchhoff Migration and Ve-locity Analysis Forconverted and non Converted Waves in Anisotropic media[J]. Geophysics, 1993, 58: 265-276.

[5]Julian B R, Gubbins D. Three Dimensional Seismic Ray Tracing[J]. Geophysics, 1977, 43: 95-119.

[6] Cerveny V. Seismic Ray Theory[M]. Cambridge: Cam-bridge University Press, 2001.

[7] Moser T J. Shortest Path Calculation of Seismic Rays[J]. Geophysics, 1991, 56: 59-67.

[8] Asakawa E, Kawanaka T. Seismic Ray Tracing Using Linear Traveltime Interpolation[J]. Geophysical Prospecting, 1993, 41(1): 99-111.

[9] 陈景波,秦孟兆.辛几何算法在射线追踪中的应用[J].数值计算与计算机应用,2000, 43(4): 254-265.

Chen Jingbo, Qin Mengzhao. Ray Ttacing by Symplectic Algorithm[J]. Journal on Numerical Methods and Computer Applications, 2000, 43(4): 254-265.

[10] 罗明秋，刘洪，李幼铭.地震波传播的哈密顿表述及辛几何算法[J].地球物理学报，2001, 44(1)： 120-127.

Luo Mingqiu, Liu Hong, Li Youming. Hamiltionian Deacription and Symplectic Method of Seismic Wave Propagtion[J]. Chinese Journal of Geophysics, 2001, 44(1): 120-127.

[11] Vinje V, Iversen E G, Joystdal H. Traveltime and Amplitude Estimation Using Wavefront Construction[J]. Geophysics, 1993, 58(8): 1157-1166.

[12] 石秀林，孙建国，孙辉，等. 基于波前构建法的时间域深度偏移：Delta波包途径[J].吉林大学学报(地球科学版)，2016，46(6)：1847-1854.

Shi Xiulin, Sun Jianguo, Sun Hui, et al. Depth Migration in Time Domain Using Wavefront Construction: Delta Packet Approach[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(6): 1847-1854.

[13] 孙章庆. 复杂地表条件下地震波走时计算方法研究[D].长春：吉林大学，2008.

Sun Zhangqing. Study on the Computation Method of Seismic Traveltimes Including Surface Topography[D]. Changchun: Jilin University, 2008.

[14] Vidle J. Finite-Difference Calcaulation of Traveltimes[J]. Bull Seism Soc Am, 1988, 78(6): 2062-2076.

[15] Sethian J A, Popovici A M. 3-D Traveltime Com-putation Using the Fast Marching Method[J]. Geophysics, 1999, 64(2): 516-523.

[16] 张东,张婷婷,乔友锋，等. 三维旅行时场B样条插值射线追踪方法[J]. 石油地球物理勘探,2013, 48(4): 559-566.

Zhang Dong, Zhang Tingting, Qiao Youfeng, et al. A 3-D Ray Method Based on B-Spline Traveltime Interpolation[J]. Oil Geophysical Prospecting, 2013, 48(4): 559-566.

[17] Nolet G. A Breviary of Seismic Tomography: Ima-ging the Interior of the Earth and Sun[M]. Cambriage: Cambriage University Press, 2008.