工程地震折射波解释方法研究进展

刘四新，朱怡诺，王旭东，宋二乔，贺文博

吉林大学地球探测科学与技术学院，长春 130026

0 引言

地震波在向介质中传播的过程中，当遇到地层界面下伏地层速度高于上覆地层速度，且入射角大于或等于临界角时会发生地震波的折射，地震波沿折射界面滑行，并在上覆介质中产生折射波。区别于研究地壳结构的宽角折射勘探(勘探深度一般为几千米至几十千米不等，纵波主频一般为几赫兹至几十赫兹不等)，工程地震折射波勘探的深度一般在1 km以内，纵波主频可达150 Hz以上。工程地震折射波勘探记录在地表激发并在近地表地质结构中传播后返回地面的人工地震波，从记录中获得波到达地面的时间，即波的旅行时，通过选取不同的折射波解释方法来推算地下不同岩层分界面的埋藏深度、倾角、地层速度等要素，从而了解近地表地层的物理参数和地质形态。

近年来，针对近地表地质勘查的工程地球物理方法受到越来越广泛的关注，包括地震勘探、电磁勘探、电法勘探、磁法勘探以及地质雷达等。在浅层地震勘探中，常使用的方法有折射波勘探法、反射波勘探法以及面波勘探法等。折射波勘探法是一种使用较久且成熟的方法，它使用大震源，能快速覆盖长距离用以探测近地表目标，且能够刻画存在明显速度对比的隆起构造，具有操作简单、工作效率高、初至波易于识取、解释方便等优点，这些都是反射波法无法比拟的。

浅层地震折射波法早在20世纪30年代就已出现并广泛应用于民用工程勘探。折射波法由石油地震勘探引用而来，因而在最开始的勘测中，震源和检波器都沿用原有的设备。到1940年时，形成了针对地震折射波的标准纵测线观测系统。20世纪50年代，折射波勘探的各种技术方法和专用仪器取得了突破性的进展。20世纪70—80年代期间，折射波勘探解释方法由低精度、低效的人工解释发展为高精度、高效的计算机自动化解释[1-2]。

目前工程折射波法常用来探测覆盖层厚度[3]，研究基岩面起伏[4]，识别隐伏断层，测量潜水面深度，探测地下空洞和隧道[5]。Rucker[6]指出地震折射波方法可以为工程地质应用提供有效的近地表地质信息；王洪[7]在实际勘测中提出并应用了一套工程地震折射波勘探方法，在堤坝病害勘查中取得了很好的效果。

传统的地震折射解释方法将近地表介质解释为每层都有一个单独速度的简单离散层状结构，基于这个假设，通过测量地震折射波的走时数据便可以获得每层的层厚和地层倾角。近年来，地震折射波处理解释方法取得了进展，产生了一种新的解释方法，即折射层析成像技术(SRT)，该方法通过对地震剖面进行网格剖分实现了获得连续变化的地震波传播速度。SRT成为对地震波传播的物理特性进行三维成像的主要方法之一[8]。近年来的一些研究证明了SRT在近地表速度模型和地下探测的高适用性，他们指出在识别速度纵横向变化梯度方面，SRT比传统折射解释方法取得了更好的效果[9]。

本文介绍了常用折射波解释的方法原理，着重介绍了折射层析成像方法，并阐述了这些方法各自的优缺点及适用性，同时对国内外工程地震折射波解释方法的发展历程及现状进行阐述。

1 方法原理

工程地震折射波解释主要用于研究近地表介质的速度、层厚及结构，可分为根据已知的勘测结果估计地下结构的定性解释，及依据定性解释的结果通过具体方法进行计算得到准确地下结构的定量解释。

折射波解释方法也可分为解析法[10-18]和数值法[19]两大类(图1)。解析法发展较早，包括波前法[10]、延迟时间法(又称时间项法)[11]、截距时间法[12]、哈莱斯法[13]、共轭点法[14]、t0差数法(又称加减法、ABC法)[15]、互换法(即表层剥去法、去表层法)[16]、广义互换法[17]、褶积成像法[18]等；数值法则较晚，其中应用最多的是折射层析成像[19]，一般是先给定初始模型，对初至波进行射线追踪，采用线性非线性算法进行反演确定最接近实际地层介质的属性结构。折射波解释的数值方法取决于地层模型、射线追踪方法和最优化算法。该类方法精度更高、效果更好、更针对复杂结构。在各类地震折射波法中，折射波层析成像是目前的研究热点和未来趋势。

1.1 波前法

波前法又称时间场法，是Thornburg[10]根据惠更斯原理提出的一种基于斯奈尔定理的图解法。Baumgarte[20]对波前法进行过论述，认为这类方法是最精确的折射解释技术，但是过于麻烦费时。经Schenck[21]改进后，画波前面的时间大大减少，更适用于数字处理技术，但实际应用仍较少。

波前法利用波场外推公式分别计算出地下介质中各网格点的地震波到时重建地震波走时场，并可获得各个时刻的波前位置。设t1(x,z)和t2(x,z)分别表示正反向走时场，T表示相遇观测系统的互换时间，折射界面上任意点R到时满足

t1(xR,zR)+t2(xR,zR)=T。

(1)

式中：xR表示点R横坐标；zR表示点R纵坐标。则可据此找出折射界面的位置。折射层的速度可由重构的波前传播时间估算，即用界面上两点之间的距离除以两点间重构的波前时间差值。

图1 折射波解释方法发展历程Fig.1 Progress of refraction interpretation method

原则上这个方法适用于任意多层情况，通过递推的方法顺序求出各层参数。但如果目的层以上的地层较为简单，那么波前法和截距时间法、加减法同样能解决问题。当存在隐蔽层和速度剧烈变化的地层时，圆弧形波前不适用上述情况，因此波前法精度低于理论值。波前法是t0差数法和哈莱斯法的基础。

1.2 延迟时间法

延迟时间法又称时间项法[11]。延迟时间是指观测临界折射时间(校正到一个基准面上的时间)与假设该折射面移至地表或基准面时所应有的折射时间之差。主要步骤为：1)校正全部波至时间并给定折射波速度；2)计算收发点的延迟时间并进行时深转换。该方法操作和校正简便，但由于求取速度方法始终不佳及对倾角敏感等原因，近年来已经不常使用。

1.3 截距时间法

截距时间法由Ewing等[12]首先提出，后来Adachi[22]、Mota[23]、Jonhson[24]又用模型，即深度和射线路径参数给予了说明。

根据截距时间法折射波时距曲线图(图2)可知，直达波时距曲线斜率的倒数为覆盖层速度v1，折射波时距曲线斜率的倒数为折射层速度v2，S1、S2分别为炮点O1、O2产生的初至波时距曲线。将折射波时距曲线的截距t01与t02定义为截距时间，由此可算出t01、t02处折射界面的法线深度h1与h2。

(2)

再分别以Oi为圆心，以求出的hi为半径做弧，则这两个弧的公切线即为折射界面。

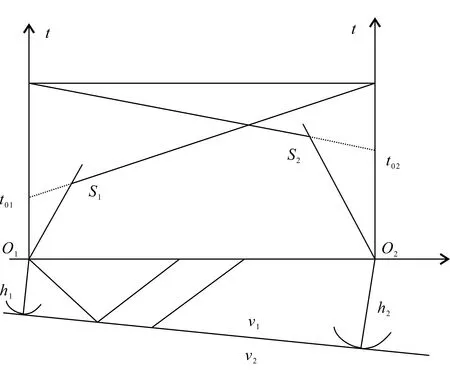
图2 截距时间法原理图Fig.2 Principle of intercept time method

该方法仅适用于地层界面为水平或倾斜的平界面、地表无起伏且速度无横向变化(即每层速度为定值)的浅层地震解释。对于浅层界面，该方法误差较小，但对于深层界面或有薄夹层时，误差较大。然而实际地形常有起伏，折射界面深度与炮点处深度不尽相同，截距时间法近年来在实际中应用很少；因而发展出了加减法、互换法等适用于起伏界面的方法。

1.4 哈莱斯法

哈莱斯法通过作图计算临界折射时间，再求取折射界面深度进行构造解释[13]。

如图3所示，O1、O2为炮点，M、N为接收点，P为折射界面上任意点，界面倾角为φ，O1APN和O2BPM为相遇折射波射线路径，过P点作界面的垂线，交地面于O点，过M、N分别做PO的垂线交PO于E、F，以MN为底边，以临界折射角ic为底角作等腰三角形MNQ，可以证明Q点在PO的延长线上。以一系列Q点为圆心，相应的PQ为半径作弧，这些弧的包络面即为所求界面。

哈莱斯法适合地表平整、折射界面起伏剧烈、下伏地层速度存在差异的情况，王奇[25]将其应用于实测中取得较好的效果(图4)，但必须已知上覆地层速度；当存在隐蔽层、变速层时效果不理想，且不易于作图。

1.5 共轭点法

针对哈莱斯法的问题，发展出了共轭点法[14]，即用共轭点的方法求取M、N，再与哈莱斯法结合进行计算。陈滋康[26]用其对实测数据进行解释，并实现了计算机自动处理。该方法无需已知覆盖层和折射层速度，只根据一组相遇时距曲线即可求解，然而要求在剖面上至少有一个点的界面深度是已知的。

图3 哈莱斯法原理图Fig.3 Principle of Hales method

1.6 t0差数法

t0差数法在最初称为加减法，又称ABC法，是由Hagedoorn[15]提出的基于几何地震学原理来求取倾角较小均匀层界面的一种方法，其实质是在每一个检波器处使用截距时间法。该方法定义了加、减两个时间值，加时间线描绘了折射层界面形状，减时间线可用于求取折射层速度。

如图5所示，i为入射角，3对炮检距射线路径分别为O1ABS、O2DCS和O1ADO2，定义t+和t-为：

t+=tO1ABS+tO2DCS-tO1ADO2，

(3)

t-=tO1ABS-tO2DCS+tO1ADO2。

(4)

式中，tO1ABS、tO2DCS和tO1ADO2分别是对O1ABS、O2DCS和O1ADO2射线路径测得的地震波初至时间。则折射层速度v2为

(5)

S点处界面埋深h为

(6)

依次类推可获得测线上全部点的界面埋深。

该方法在界面的曲率半径远大于其埋深的情况下效果很好，适用于简单不规则起伏界面和界面两侧地震波速度变化较大的界面，但不适用于倾角大于10°的情况，且横向速度不能有明显变化。t0差数法比波前法速度快、使用成本低，是目前使用最为广泛的浅层折射波勘探方法。熊章强等[27]将该方法应用于隧道勘查，得到了准确的基岩埋深和各地层速度信息；彭骁等[28]在候家梁隧道工区探测中取得了较好的效果；包勋等[29]成功利用t0差数法探测到隐伏断层的位置和分布情况(图6)。

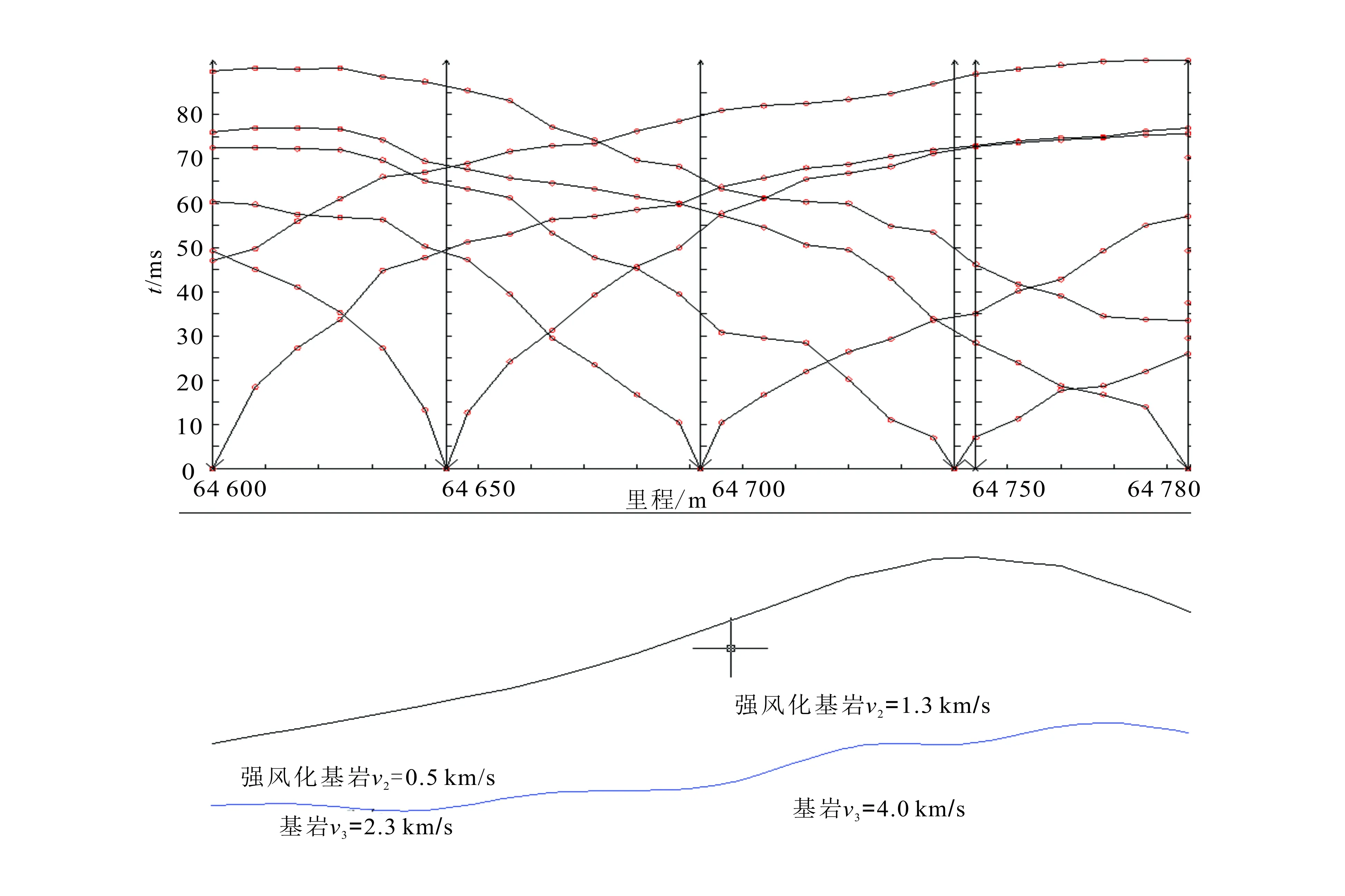
据文献[25]。图4 辽宁鞍山境内某隧道哈莱斯法解释图Fig.4 Interpretation of a tunnel in Anshan, Liaoning Province

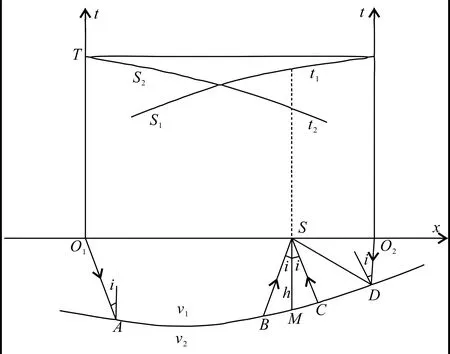
图5 t0差数法原理图Fig.5 Principle of t0difference method

1.7 互换法

互换法又称表层剥去法、去表层法，应用起来最为简洁并能估算折射层结构和速度情况[16]。

该方法引入了延迟时的概念。如图7所示，将A点延迟时定义为烈时，可得到更准确的深度；但当存在大构造时，解释界面因虚假速度变得圆滑。该方法与t0差数法结合使用，可求取界面深度小于25 m的地层。王奇[25]将其应用于隧道探测中，与t0差数法进行比较取得了相似的效果(图8、9)。

(7)

则A点下折射界面深度为

(8)

根据几何方法，可得D点延迟时间：

(9)

可见，延迟时tD等于t0差数法t0的一半，也是截距时间的一半。当深度无较大起伏且速度差异剧

据文献[29]。图6 某水库折射波综合时距曲线及t0差数法解释剖面结果图Fig.6 A reservoir refraction synthetical traveltime and profile result for t0 difference method

图7 互换法几何路径图Fig.7 Geometric path diagram of reciprocal method

1.8 广义互换法

广义互换法是互换法的拓展，也需要正反两个时距曲线，其计算速度和时间深度的公式与传统互换法相似，但增加了一个补偿项进行偏移校正处理[17]。

如图10所示，X、Y为接收点，如果地表上的D点与接收点不重合，则D点延迟时为

(10)

(11)

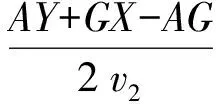
广义互换法大致可分为3个过程：1)求取速度分析函数；2)求取时深偏移函数；3)选取最佳XY值。该方法通过选取最佳XY值并带入步骤1)和2)中的函数可求出折射层速度和深度。当XY=0时，广义互换法即为通常意义上的互换法，可能会导致虚假折射速度大量出现，并使得有起伏折射面的细节被圆滑掉。该方法处理倾角小于20°的界面效果一般，而应用于大倾角、存在横向速度变化或隐蔽带时效果较好[31]。Sjögren[32]尝试将广义互换法用于浅层工程调查中并与哈莱斯法进行比较，验证了其适应性，并总结了勘查过程中可能会遇到的问题(图11)。

据文献[25]。图8 辽宁鞍山境内某隧道折射波互换法解释图Fig.8 Interpretation of reciprocal method of a tunnel in Anshan, Liaoning Province

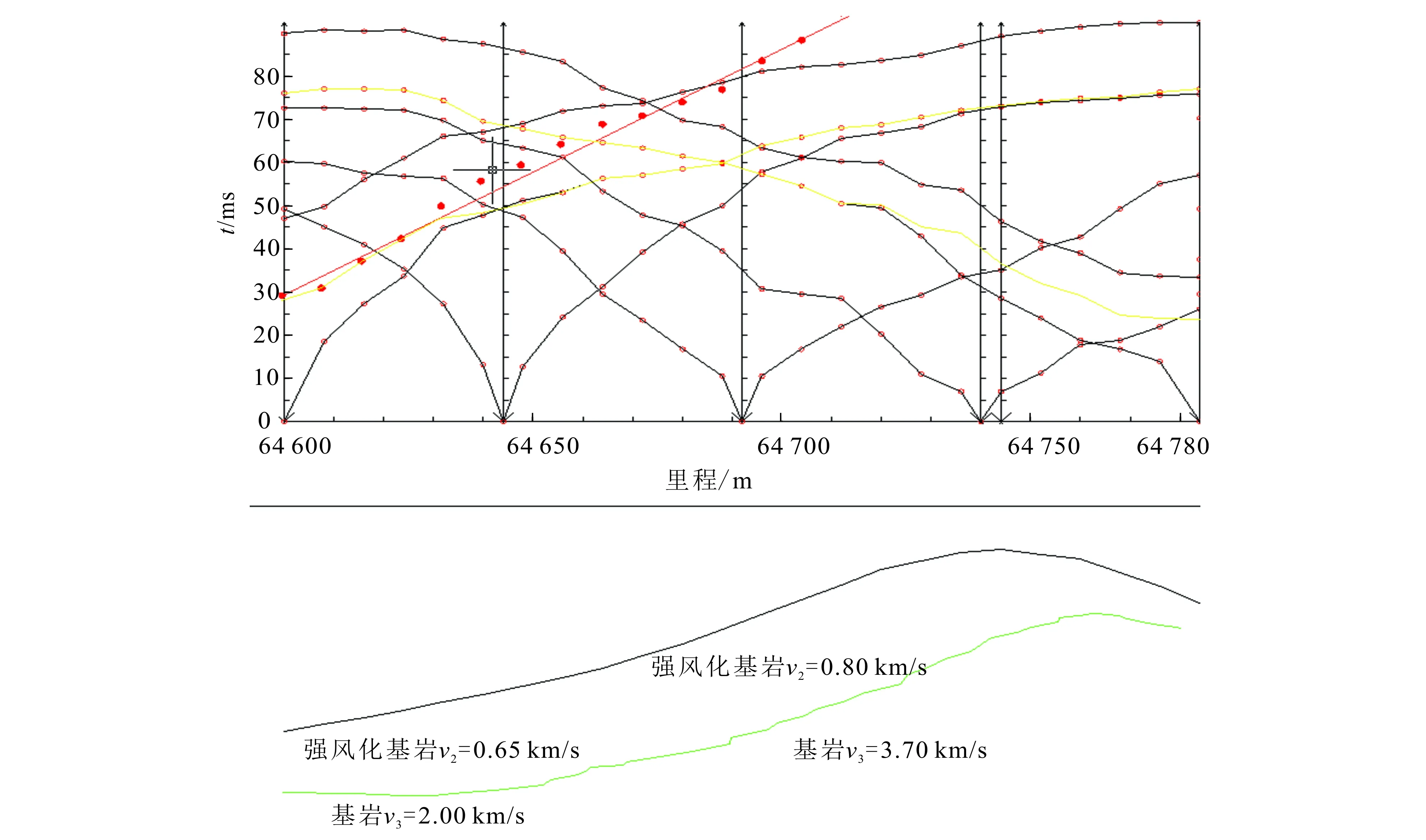
据文献[25]。图9 辽宁鞍山境内某隧道折射波t0差数法解释图Fig.9 Interpretation of t0difference method of a tunnel in Anshan, Liaoning Province

图10 广义互换法确定延迟时原理图Fig.10 Principle of generalized reciprocal method to calculate delay time

1.9 褶积成像法

Palmer[18]提出了运用褶积的浅层地震折射波处理方法，同年考虑了几何扩散的影响，对折射波褶积成像法做出了改进。该方法不需要拾取初至时间，可以直接将同一点处的正向和反向走时数据进行褶积得到走时数据的交叉时，再利用速度求出该点的垂向深度。Franco[33]提出了利用褶积和互相关运算对数据叠加来提高信噪比的方法，并对多个折射界面成像，是常规解释方法的一大突破(图12)。

1.10 折射波层析成像

层析成像技术最先用于医学，随后拓展到地球物理学界。Aki等[34]最早提出地震走时层析成像方法，并应用于美国某地区的地壳结构探测。Hearn等[19]利用6年的天然地震数据首次实现了折射波层析成像。

在工程地震层析成像方法中，目前应用较多的是基于射线理论的折射波走时层析成像。与传统折射波法相比，折射波层析成像的优势在于对速度纵横向有较大变化的地层、大倾角地层、隐伏层、界面起伏层等情况反演结果很好。

地震折射波层析成像计算流程主要包括初至走时提取、速度模型建立、正演、迭代反演4个步骤。

1.10.1 初至走时提取

地震勘探中把经过地下介质首先到达检波器的波称为初至波，这些波的旅行时包含了浅层速度信息，具有易于获取、能量强、可追踪性好的优点[35]。初至波走时的准确拾取构成了折射层析成像的基础和前提。

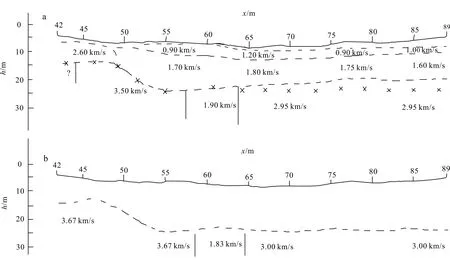
a. 哈莱斯法；b. 广义互换法。据文献[32]。图11 速度和深度解释结果图Fig.11 Results of speed and depth interpretation

据文献[33]。图12 意大利北部克卢索内盆地实测数据Fig.12 Application to real data of Clusone basin area in Northern Italy

1.10.2 速度模型建立

走时层析成像的效果和收敛速度依赖于初始速度模型，建立近地表初始速度模型的方法一般有3种：1)人工给定常速度初始速度模型；2)根据工区已有的速度资料确定初始速度模型；3)利用直达波和折射波初至时间自动求取初始速度模型(该模型每层速度都是常数，在此基础上可以进行层间速度的反距离加权差值计算，获得纵向渐变的初始速度模型)[36]。段心标等[37]在此基础上提出一种生成模型网格节点的初始速度方法。刘玉柱等[38]通过研究波形反演目标函数性态分析，验证了初至波走时层析成像对初始模型的依赖性，讨论了简单、高效的层析初始模型选取问题。

1.10.3 正演

地震层析成像对正演计算要求很高，其精度和速度对成像的分辨率和可靠程度具有很大影响。常用两种数值模拟：其一是以射线理论为基础的射线追踪法；其二是以波动理论为基础的波动方程数值模拟。由于计算上的优势，目前折射波层析成像主要为射线理论层析成像方法。

1)射线追踪法

基于射线理论的地震波走时层析成像方法是因其直观性、高效率、模型强适应性而被应用的一种波场近似算法，主要有两种经典的算法：试射法(打靶法)[39]和弯曲法[40]。在此基础上发展演化出了两大类现代算法：一是基于全局算法的最短路径法[41]和线性走时插值算法[42]，在计算过程中同时考虑所有离散点上的走时和射线路径；二是基于局部算法，在射线追踪过程中只考虑两点间的走时和射线路径。

试射法是根据斯奈尔定理，通过不断调整震源点处的射线角来完成对接收点的追踪，进而确定射线路径。这种方法能精细地处理弯曲界面，适用于一般各向异性介质的多值走时计算，但对于复杂的地质模型存在阴影问题。

弯曲法是根据费马原理，通过调整假定参数以达到震源与检波点间走时最小的一种方法。这种方法虽然不存在阴影区，但用于局部复杂的介质模型会收敛到局部最小值，且计算效率和精度较低。

最短路径法又称最小走时树法，由Nakanishi等[41]提出，由Moser[43]、Cheng[44]改进。该方法基于惠更斯原理和网格理论，计算从震源到模型中所有网格点的走时和射线路径，给出震源到接收点所有可能的最小走时节点和射线路径，保证了全局收敛性，简单且稳定，不会错过任何一个接收点。

线性走时插值法由Asakawa等[42]提出，由Cardarelli等[45]、张东等[46]改进，包括两个步骤：正向计算所有网格节点的走时；反向追踪所有收发排列的射线路径。这种算法的精度和计算效率都很高。

基于局部算法的射线追踪技术中最具代表性的是基于程函方程有限差分解的射线追踪方法[47]，其思想是把射线追踪问题分为正向计算波前走时和反向追踪射线路径两个步骤。该方法计算速度快，不存在传统方法具有的阴影问题；但当局部速度变化过大时计算可能出现负数开方问题，导致算法不稳定，且其扩展方式不符合波前传播的物理规律。基于此，一些学者研究发展出了快速扫描算法(fast sweeping method)[48]、快速推进算法(fast marching method)[49]、高精度快速推进算法[50]、基于多模块快速推进算法(multistencils fast marching method)[51]。

2)波动方程数值模拟

射线路径无法被准确地追踪到，其原因可能是构造较复杂，或存在间断面；而波动方程法正演具有波场齐全、信息丰富的特点，缺点在于费时。地震波场的正演模拟是利用不同算法求解变系数偏微分方程的过程。目前求解方法包括有限差分法[52]、有限元法[53]、伪谱法等。在实际应用中通常根据实际情况综合各种方法达到计算目的。

1.10.4 迭代反演

迭代反演通过求解震源和介质参数的方程来获得模型参数，将每次反演出的数据与实测数据相比较，不断迭代直到两者误差达到精度要求。反演方法可以分为两类：第一类是基于算子的线性反演方法，包括代数重建技术(ART)[54]、联合迭代重建法(SIRT)[55]、奇异值分解法(SVD)[56]、最速下降法、共轭梯度法[57]、最小二乘法(如最小二乘正交分解法(LSQR)[58]、极小残量法(GMRES)[59]和双稳定共轭梯度法(BICGSTAB)[60]等)、阻尼最小二乘法[33]等；第二类是基于模型的完全非线性反演方法，包括遗传算法[61]、模拟退火法[62]和神经网络法等。非线性反演方法虽然对于复杂问题效果更为明显，但是计算效率低，因而目前在地震体波层析成像中，线性反演方法应用更为广泛。Liu等[63]通过结合线性和非线性方法，提出了Two-step MCMC方法，效果很好。

赵昭等[64]同时使用反射和折射2种走时资料，在改善层析成像水平和垂向分辨率上取得了较好的效果。崔岩等[65]提出了用于反演的初至波走时层析成像的Tikhonov正则化模型和一种层析成像的梯度优化算法，数值实验表明，该方法适用于速度差别的任意模型，且求解稳定易于实现。Pegah[66]将折射波层析成像与面波多通道分析相结合，进行近地表岩土工程研究，取得了较好的效果。

2 发展前景

目前，工程地震折射波法更多是用来对未知地区做作初步调查，在极浅层(即勘探深度为几米至几十米)和硬岩勘探中有着较大优势，如要成为被公认的勘探技术，仍需要结合各个反演解释方法的利弊发展成一套综合的解释方法，使之适应大多数实际情况，而不是分类列举各种巧妙技术。这些方法的发展表明折射波法的发展趋势是勘探深度不断增加、应用范围不断推广和复杂程度不断提高。勘探特点趋向于近地表非均质极强、各向异性明显、地形起伏大、勘探深度小和精度要求高，要求工程地震折射波法有更高的分辨率、信噪比、保真度。

由于浅层横波勘探分辨率高，对地层结构成像效果好但不易激发，而纵波勘探深度大且易于激发，但其成像效果差。因此，利用二者特点，研究多波联合处理解释对增加工程地震折射波勘探的精度和分辨率，以及减少反演结果的不确定性具有意义重大。

以折射层析成像研究为代表的解释方法研究和观测系统研究，是增加多层折射介质成像精度的重点方向。

3 结论

本文概述了现有的几种折射波反演解释方法，当探测深度较浅(5 m左右)且分界面足够平整、界面倾角较小时，最方便的解释方法是截距时间法；当勘探目标的深度达到25 m时，t0差数法最为适用；对于勘探目标埋深超过25 m时，为了不抹平界面的不规则性、避免产生虚假的折射速度，应当使用广义互换法；波前法、哈莱斯法、延迟时间法等或者原理与之类似，或者效率和方便程度等综合效果不如以上3种方法。以上的常规折射波解释方法都需要求取正向和反向的旅行时之和，且实际数据存在大量噪音，人工提取走时存在困难，准确率不够高；而折射波褶积成像避免了拾取走时的过程，节约时间且效果较好。随着勘探精度要求越来越高，使用折射波走时层析成像技术可以满足近地表介质速度纵横向变化的地层、大倾角地层、隐伏层、界面起伏层等情况。

[1] 北京铀矿地质研究所浅层地震组. 浅层地震探测方法与技术[M]. 北京：原子能出版社，1982:41-84.

Shallow Seismic Group of Beijing Institute of Uranium Geology. Methods and Techniques for Shallow Seismic Detection[M]. Beijing：Atomic Energy Publishing House, 1982: 41-84.

[2] 熊章强，方根显. 浅层地震勘探[M]. 北京：地震出版社，2002:79-90.

Xiong Zhangqiang, Fang Genxian. Shallow Seismic Exploration[M]. Beijing: Seismological Press, 2002: 79-90.

[3] 葛双成，李小平，邵长云，等. 地震折射和电阻率法在水库坝址勘察中的应用[J]. 地球物理学进展，2008，23(4): 1299-1303.

Ge Shuangcheng, Li Xiaoping, Shao Changyun, et al. Application of Seismic Refraction and Resistivity for Exploration of Reservoir Dam Site[J]. Progress in Geophysics, 2008, 23(4): 1299-1303.

[4] 喻岳钰，曹代勇，邢春颖，等. 黄土塬区模型约束折射静校正技术应用研究[J]. 地球物理学进展，2016，31(3): 1373-1380.

Yu Yueyu, Cao Daiyong, Xing Chunying, et al. Application of the Technology of Model Constraint Refraction Statics on Loess Area[J]. Progress in Geophysics, 2016, 31(3): 1373-1380.

[5] Steven D S, Jeffery J N, Seth W, et al. Using Near-Surface Seismic Refraction Tomography and Multichannel Analysis of Surface Waves to Detect Shallow Tunnels: A Feasibility Study[J]. Journal of Applied Geophysics, 2013, 99: 60-65.

[6] Rucker M L. Integrating Seismic Refraction and Sur-face Wave Data Collection and Interpretation for Geotechnical Site Characterization[C]// Conference on Applied Geophysics. Missouri: Geophysics, 2006.

[7] 王洪. 折射波法在堤坝病害探查中的应用研究[D]. 长沙：中南大学，2007.

Wang Hong. Study on the Application of Refraction Wave Method in Disease Detection of Embankments and Dams[D]. Changsha: Central South University, 2007.

[8]Thurber C, Ritsema J. Theory and Observations: Seismic Tomography and Inverse Methods[J]. Treatise on Geophysics, 2007, 1: 323-360.

[9] Sheehan, Jacob R, William E, et al. An Evaluation of Methods and Available Software for Seismic Refraction Tomography Analysis[J]. Journal of Environmental and Engineering Geophysics, 2005, 10(1): 21-34.

[10] Thornburgh H R. Wave-Front Diagrams in Seismic Interpretation[J]. American Association of Petroleum Geologists Bulletin, 1930, 14: 185-200.

[11] Gardner L W. AnAreal Plan of Mapping Subsurface Structure by Refraction Shooting[J]. Geophysics, 1939, 4(4): 247.

[12] Ewing M,Woollard, Vine A C, et al. Geophysical Investigations in the Emerged and Submerged Atlantic Coastal Plain: Part IV: Cape May, New Jersey, Section[J]. Geological Society of America Bulletin, 1940, 51: 1821-1840.

[13] Hales F W. An Accurate Graphical Method for Inter-preting Seismic Refraction Lines[J]. Geophysical Prospecting, 1958, 6(3): 285-294.

[14]Гамбурцев Г A. Основы Сейсморазведки Гостоптех- Издаг Москва[M]. Матемсб: Гостоптехиздат, 1959.

[15]Hagedoorn J G. The Plus-Minus Method of Inter-preting Seismic Refraction Sections[J]. Geophysical Prospecting, 1959, 7(2): 158-182.

[16]Hawkins L V. The Reciprocal Method of Routine Shallow Seismic Refraction Investigations[J]. Geophysics, 1961, 26(6): 806.

[17]Palmer D. An Introductionto the Generalized Reci-procal Method of Seismic Refraction Interpretation[J]. Geophysics, 1981, 46(11): 1508.

[18] Palmer D. Imaging Refractors with the Convolution Section[J]. Geophysics, 2001, 66: 1582-1589.

[19] Hearn T M, Clayton R W. Lateral Velocity Vari-ations in Southern California: II: Results for the Lower Crust fromPnWaves[J]. Bull Seism Soc Am, 1986, 76: 511-520.

[20]Baumgarte J. Konstruktive Darstellungvon Seismi-chen Horizon Tenunter Berock Sichtigung Der Strahlen Brechung ImRaum[J]. Geophysical Prospecting, 1955, 3(2): 126-162.

[21]Schenck F L. Refraction Solutions by Wavefront Targeting: Abstract[J]. Aapg Bulletin, 1963, 47(9): 1775-1776.

[22]Adachi R. On aProof of Fundamental Formura Concerning Refraction Method of Geophysical Prospecting and Some Remarks[J]. Kumamoto Journal of Science L Ser A: Mathematics Physics & Chemistry, 1954, 2: 18-23.

[23]Mota L. Determination of Dips and Depths of Geological Layers by the Seismic Refraction Method[J]. Geophysics, 1954, 19(2): 242.

[24] Johnson S H. Interpretation of Split-Spread Refrac-tion Data in Terms of Plane Dipping Layers[J]. Geophysics, 1976, 41(3): 418.

[25] 王奇. 浅层地震气折射波法在工程应用中的研究[D]. 成都：成都理工大学，2010.

Wang Qi. Study of Shallow Seismic Gas Refraction Wave Method in Engineering Application[D]. Chengdu: Chengdu University of Technology, 2010.

[26] 陈滋康. 用共轭点法解释折射时距曲线及其计算程序[J]. 物探与化探，1986，10(5): 350-355.

Chen Zikang. Explain Refraction Time Distance Curve and Its Calculation Procedure Using Conjugate Point Method[J]. Geophysical and Geochemical Exploration, 1986, 10(5): 350-355.

[27] 熊章强，方根显. 浅层折射波法在隧道工程地质调查中的应用[J]. 水文地质工程地质，2001，28(1): 63-66.

Xiong Zhangqiang, Fang Genxian. Application of Refractive Method in Tunnel-Engineering Exploration[J]. Hydrogeology and Engineering Geology, 2001, 28(1): 63-66.

[28] 彭骁，王鹏. 浅层地震折射波法在候家梁隧道地质勘查中的应用[J]. 工程地球物理学报，2013，10(5):631-636.

Peng Xiao, Wang Peng. The Application of Shallow Seismic Refraction to Houjialiang Tunnel Exploration[J]. Chinese Journal of Engineering Geophysics, 2013,10(5): 631-636.

[29] 包勋，汤浩，朱照拔. 综合物探技术在探测隐伏断层中的应用[J]. 人民珠江，2016，37(12): 29-32.

Bao Xun, Tang Hao, Zhu Zhaoba. Application of Comprehensive Geophysical Prospecting Method to Buried Fault Detection[J]. Pearl River, 2016, 37(12): 29-32.

[30] 张恒超，李学聪. 模型法、扩展广义互换法(EGRM)、沙丘曲线法静校正对比研究及在ZGE沙漠资料处理中的应用[J]. 地球物理学进展，2010，25(6)：2193-2198.

Zhang Hengchao, Li Xuecong. Study of Static Corrections by the Model Method, Extended Generalized Reciprocal Method (EGRM) and Sand Dune Curve Method and Their Application to Seismic Data Processing in the ZGE Area[J]. Progress in Geophysics, 2010, 25(6): 2193-2198.

[31] Tak M L. Controls of Traveltime Data and Problems of the Generalized Reciprocal Method[J]. Geophysics, 2003, 68(5): 1626-1632.

[32]Sjögren B. A Brief Study of Applications of the Generalized Reciprocal Method and of Some Limitations of the Method[J]. Geophysical Prospecting, 2000, 48(5): 815-834.

[33] Franco R D. Multi-Refractor Imaging with Stacked Refraction Convolution Section[J]. Geophysical Prospecting, 2005, 53(3): 335-348.

[34]Aki K, Lee W H K. Determination of Three‐Dimensional Velocity Anomalies Under a Seismic Array Using First P Arrival Times from Local Earthquakes: 1: A Homogeneous Initial Model[J]. Journal of Geophysical Research Atmospheres, 1976, 81(23): 4381-4399.

[35] 景月红. 地震初至波走时层析成像与近地表速度建模[D]. 西安：长安大学，2009.

Jing Yuehong. Seismic First Break Travel-Time Tomography and Its Application in Near-surface Velocity Model Building[D]. Xi’an: Chang’an University, 2009.

[36] 陈国金，高志凌，吴永栓，等. 井间地震层析成像中自动生成初始速度模型的方法研究[J]. 石油物探，2005，44(4):339-342.

Chen Guojin, Gao Zhiling, Wu Yongshuan, et al. Automatically Building the Initial Velocity Model in the Seismic Crosshole Tomography[J]. Geophysical Prospecting for Petroleum, 2005, 44(4): 339-342.

[37] 段心标，金维浚. 井间地震层析成像初始速度模型[J].地球物理学进展，2007，22(6):1831-1835.

Duan Xinbiao, Jin Weijun. Initial Velocity Model of Crosswell Seismic Tomography[J]. Progress in Geophysics, 2007, 22(6): 1831-1835.

[38] 刘玉柱，丁孔芸，董良国. 初至波走时层析成像对初始模型的依赖性[J]. 石油地球物理勘探，2010，45(4):502-511.

Liu Yuzhu, Ding Kongyun, Dong Liangguo. The Dependence of First Arrival Travel Time Tomography on Initial Model[J]. Oil Geophysical Prospecting, 2010, 45(4): 502-511.

[39] Engdahl E R. Relocation of Intermediate Depth Earth-quakes in the Central Aleutians by Seismic Ray Tracing[J]. Nature, 1973, 245(141): 23-25.

[40] Julian B R,Gubbins D. Three Dimensional Seismic Ray Tracing[J]. J Geophysics,1977, 43: 95-113.

[41] Nakanishi I, Yamaguchi K. A Numerical Experiment on Nonlinear Image Reconstruction from First-Arrival Times for Two-Dimensional Island Arc Structure[J]. Earth Planets and Space, 1986, 34(2):195-201.

[42] Asakawa E,Kawanaka T. Seismic Ray Tracing Using Linear Traveltime Interpolation[J]. Geophysical Prospecting, 2010, 41(1): 99-111.

[43] Moser T J. Shortest Path Calculation of Seismic Rays[J]. Geophysics, 1991, 56(1): 59-67.

[44]Cheng N. Minimum Traveltime Calculation in 3-D Graph Theory[J]. Geophysics, 1996, 61(6): 1895-1898.

[45]Cardarelli E,Cerreto A. Ray Tracing in Elliptical Anisotropic Media Using the Linear Traveltime Interpolation (LTI) Method Applied to Traveltime Seismic Tomography[J]. Geophysical Prospecting, 2002, 50(1): 55-72.

[46] 张东，谢宝莲，杨艳，等. 一种改进的线性走时插值射线追踪算法[J]. 地球物理学报，2009，52(1):200-205.

Zhang Dong, Xie Baolian, Yang Yan, et al. A Ray Tracing Method Based on Improved Linear Traveltime Interpolation[J]. Chinese Journal of Geophysics, 2009, 52(1): 200-205.

[47] Vidale J. Finite-Difference Calculation of Travel Time in Three Dimensions[J]. Geophysics, 1990, 55: 521-526.

[48]Tsai Y H R, Cheng L T,Osher S, et al. Fast Sweeping Algorithms for a Class of Hamilton-Jacobi Equations[J]. SIAM Journal on Numerical Analysis, 2004, 41(2): 659-672.

[49] Sethian J A. A Fast Marching Level Set Method for Monotonically Advancing Fronts[J]. Proceedings of the National Academy of Science of the United States of America, 1996, 93(4): 1591-1595.

[50] Sethian J A. Level Set Methods and Fast Marching Method[M]. Cambridge: Cambridge University Press, 1999: 400.

[51] 王飞. 跨孔雷达走时层析成像反演方法的研究[D]. 长春：吉林大学，2014.

Wang Fei. Research onCrosshole Radar Traveltime Tomography[D]. Changchun: Jilin University, 2014.

[52]Yee K S. Numerical Solution of Initial Boundary Value Problems Involving Maxwell Equations in Isotropic Media[J]. IEEE Trans Antennas Propagat, 1966, 14(3): 302-307.

[53] Yoon Y S, Yeh W G. Parameter Identification in an Inhomogeneous Medium with the Finite-Element Method[J]. Society of Petroleum Engineers Journal, 1976, 16(4): 217-226.

[54] Herman G T, Brouw W N. Book-Review: Image Re-construction from Projections: The Fundamentals of Computerized Tomography[J]. Space Science Reviews, 1980, 32(4): 56-61.

[55]Humphreys E, Clayton R W. Adaptation of Back Projection Tomography to Seismic Travel Time Problems[J]. Journal of Geophysical Research Solid Earth, 1988, 93(B2): 1073-1085.

[56] Golub G H, Reinsch C. Singular Value Decomposi-tion and Least Squares Solutions[J]. Numerische Mathematik, 1970, 14(5): 403-420.

[57] Scales J A. Tomographic Inversion via the Conjugate Gradient Method [J]. Geophysics,1987, 52(2): 179.

[58] Paige C C, Saunders M A. LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares[J]. ACM Transactions on Mathematical Software, 1982, 8(1): 43-71.

[59] Saad Y, Schultz M H. GMRES: A Generalized Mi-nimal Residual Algorithm for Solving Nonsymmetric Linear Systems[J]. SIAM Journal on Scientific and Statistical Computing, 1986, 7(3): 856-869.

[60]Sleijpen G L G, Fokkema D R. BiCGstab(ell) for Linear Equations Involving Unsymmetric Matrices with Complex Spectrum[J]. Electronic Transactions on Numerical Analysis Etna, 1993, 1(11): 1160.

[61] Amoon C J, Vidale J E. Tomography Without Rays[J]. Bulletin of the Seismological Society of America, 1993, 83(2): 509-528.

[62] Kirkpatrck S, Jr G C, Vecchi M P, et al. Optimi-zationby Simulated Annealing[J]. Science, 1983, 220: 671-680.

[63] Liu J, Braile L. Two-Step MCMC Seismic Tomog-raphy[C]// AGU Fall Meeting. San Francisco: AGU, 2004.

[64] 赵昭，赵志新，徐纪人，等. 高精度人工地震波层析成像技术勘探地下构造[J]. 吉林大学学报(地球科学版)，2011，41(增刊1):362-367.

Zhao Zhao, Zhao Zhixin, Xu Jiren, et al. Surveying Structures with High-Resolution Seismic Tomography[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(Sup. 1): 362-367.

[65] 崔岩，王彦飞. 基于初至波走时层析成像的Tikhonov正则化与梯度优化算法[J]. 地球物理学报，2015，58(4):1367-1377.

Cui Yan, Wang Yanfei. Tikhonov Regularization and Gradient Descent Algorithms for Tomography Using First-Arrival Seismic Traveltimes[J]. Chinese Journal of Geophysics, 2015, 58(4): 1367-1377.

[66] Pegah E, Liu H. Application of Near-Surface Seismic Refraction Tomography and Multichannel Analysis of Surface Waves for Geotechnical Site Characterizations: A Case Study[J]. Engineering Geology, 2016, 208: 100-113.