保障性住房项目PPP模式可行性与投资决策研究——基于博弈论

陈立文,杜泽泽

(河北工业大学 经济管理学院,天津 300401)

1 引言

保障性住房是政府为收入较低、住房困难的居民提供的低租金住房。为解决城市中低收入家庭安居这一关键的民生问题,全面实现“住有所居”目标,政府提出要不断加大力度进行保障房建设。我国高度重视,并将建设保障房作为政府未来工作的重要范畴:在“十二五”规划纲要中,政府提出要加快构建以政府为主提供基本保障、以市场为主满足多层次需求的住房供应体系[1]。党的十八大报告明确提出,“要结合政府保障以及市场配置来建立住房制度,完善保障房的建设以及管理,使住房困难群体需求得到基本满足”,这是将“保障房建设”首次写入党代会报告,可见它作为民生问题的重要性。2017年住建部等部门再推“购租并举”,加大租房市场供应,以缓解房价上涨压力。但是我国保障性住房建设存在融资困难、效率底下等问题,这些问题制约着保障性住房的顺利建设。采用PPP模式建设保障性住房能有效改善保障性住房资金缺口大的状况,稳定社会经济发展。近年来,政府颁布了一系列文件鼓励PPP模式应用于公共设施建设等领域,2015年5月六部委印发相关文件首次明文鼓励地方运用PPP模式实现公共租赁房建设[2],因此宽松的政策环境加上充足的社会资本为PPP模式应用于保障性住房项目创造了条件。

PPP模式在保障性住房建设中的应用是当今学术界研究的热点。当前的研究成果主要集中在PPP模式在我国保障性住房方面的可行性与适用性研究,并且大多以定性研究为主,缺少相应的定量研究,也缺少对多种不同PPP模式细分下的投资决策研究[3-6]。周雪峰[7]以河南省为例分析了PPP模式在保障性住房项目中的可行性,设计了PPP模式的运作流程并从政策、税金优惠、金融支持三方面给出了建议;刘广平等[8]分别针对产权型保障性住房和租赁型保障性住房构建了在PPP模式下的社会资本投资决策模型,并给出吸引社会资本参与保障性住房建设的政策建议;郝生跃[9]等探索了我国“十三五”时期的保障性住房建设模式,提出了针对保障性住房建设更完善的PPP模式;张明宇[10]借鉴英国的PPP模式在保障性住房建设中的应用经验,探讨了PPP模式在我国保障房建设中的适用性，并给出了相关建议。

根据田礻韦萌[11]等人的研究成果,PPP模式不适用于产权型保障性住房项目,仅适用于租赁型保障性住房项目。适用于租赁型保障性住房的PPP模式主要有四种:BOT、TOT、完全私有化和部分私有化。本文选取完全私有化中的BOO模式和部分私有化中合资建设模式进行研究。研究构造了保障性住房项目四种PPP模式的投资回报率模型,以判断PPP模式的可行性；同时，构造了四种PPP模式的投资决策模型,在判断可行性的基础上得出企业的最优决策。此外,本文采用等额年金法对四种PPP模式进行了比较优选,改进了投资回报率未考虑时间因素的不足,最后用案例进行应用研究并给出了相关对策建议。

2 研究假设

投资回报率是企业通过投资所获得的经济回报,投资回报率越高,表示每单位投资获得的企业价值越高,投资效果越好[12]。企业根据项目投资回报率与该行业投资回报率做对比,判断项目是否可行,从而进行项目的选择决策。在构建保障性住房项目PPP模式下的投资回报率模型和博弈模型前的假设为:假设1——企业参与投资的保障性住房项目全部租赁,即入住率为100%,保障性住房项目在运营期结束后残值为零。假设2——项目初始建设成本在不同PPP模式下相同,在选定需要建设的保障性住房项目时即可确定,建设成本在项目建设初期一次性投入。不同PPP模式下的项目建设期相同,不同PPP模式下的保障性住房项目运营效率相同,即运营成本相同且每年的运营成本不变;不同PPP模式下政府给予的税金优惠相同,同时给予优惠后的税金每年保持不变。假设3——企业参与投资保障性住房项目的收入主要是租金收入,忽略其他收益来源。租金收入以名义租金计算,实际租金为租户实际缴纳的租金,名义租金与实际租金的差额由政府补贴,即企业参与投资保障性住房项目过程中的租金收入一定等于名义租金，不同PPP模式下的名义租金相同且每年保持不变。同时,企业参与投资保障性住房项目的收益率必须满足企业要求的收益率,要求收益率由企业根据行业水平确定。假设4——构建的保障性住房项目PPP模式下的投资回报率模型是评价企业盈利能力的静态指标,未考虑资金的时间价值,但不影响政府与企业间的投资博弈,同时不考虑企业的社会资本融资问题。

3 模型建立与求解

投资回报率为利润总投入比,以ROI表示,则:

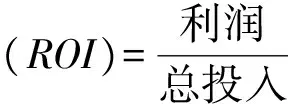
(1)

若项目可行,则需要项目投资回报率大于该行业最低投资回报率,即:

ROI≥ROI行MIN

(2)

本文假设政府自行建设保障性住房项目的建设成本为I,土地成本为L1,建筑面积为S(m2)需缴纳的税金为TAX1(元/a),运营成本为Q(元/a),项目建设期为t1,运营期为t2,向租户实际收取租金为P1(元/a·m2)。若企业采用BOT模式投资参与保障性住房项目,假设优惠后的土地成本为L2,优惠后需缴纳的税金为TAX2(元/a),名义租金为P2(元/a/m2),特许经营期为t3,特许经营期转交给政府后的政府剩余经营期为t4,由假设可知t2=t3+t4。

3.1 采用BOT模式参与保障房项目

由假设可得BOT模式下的企业投资回报率为:

(3)

若ROI1>ROI行,则该模式可行。企业采用BOT模式参与保障房项目时,企业会与政府谈判特许经营期的期限长度以期获得企业收益最大化。根据假设可知企业参与投资保障性住房项目必须满足其要求的收益率,即企业此时的净现值不小于要求的收益,设要求收益率为R,则:

NPV1≥(I+L2)R

(4)

即:NPV1≥(P2S-Q-TAX2)(P/A,i,t3)(P/F,i,t1)-(I+L2)≥(I+L2)R

(5)

式中,左边为企业在BOT模式下的收益净现值,其中第一项为企业收益现值,第二项为项目建设初期总投资,右边是企业要求收益;(P/A,i,t)为年金现值系数;(P/F,i,t)为复利现值系数，此时企业与政府为了各自利益存在博弈关系。

政府的净收益为:

E1=(P2S-Q-TAX2)(P/A,i,t4)(P/F,i,t3)(P/F,i,t1)-S(P2-P1)(P/A,i,t2)(P/F,i,t1)+TAX2(P/A,i,t3)(P/F,i,t1)+L2

(6)

式中,右边第一项为企业以BOT模式参与保障性住房项目的政府剩余经营期间的收益现值；第二项为政府租金补偿现值；第三项为企业支付政府税金现值；第四项为企业支付的土地成本。

政府的期望收益函数为:

(7)

将式(5)和式(6)带入式(7),并引入拉格朗日因子λ1构造拉格朗日函数为:

L(t2,λ1)=(P2S-Q-TAX2)(P/A,i,t4)(P/F,i,t3)(P/F,i,t1)-S(P2-P1)(P/A,i,t2)(P/F,i,t1)+TAX2(P/A,i,t3)(P/F,i,t1)+L2+λ1[(P2S-Q-TAX2)(P/A,i,t3)(P/F,i,t1)-(I+L2)-(I+L2)R]

(8)

(9)

3.2 采用BOO模式参与保障房项目

若企业采用BOO模式投资参与保障性住房项目,假设在满足企业要求收益的基础上,多余的收益以一定比例返还给政府,返还比例为k,则BOO模式下企业的投资回报率为:

(10)

若ROI2>ROI行,则该模式可行。企业采用BOO模式参与保障性住房投资时,为保障企业收益,需与同政府谈判现金流返还比例,同时企业收益也需满足要求的收益,则:

NPV2≥(I+L2)R

(11)

NPV2=(P2S-Q-TAX2)(1-k)(P/A,i,t2)(P/F,i,t1)-(I+L2)≥(I+L2)R

(12)

式中，左边为企业在BOO模式下的净现值,其中第一项为企业收益现值,第二项为项目建设初期总投资；右边是企业要求的收益。此时,企业与政府存在博弈关系,政府的净收益为:

E2=(P2S-Q-TAX2)k(P/A,i,t2)(P/F,i,t1)-S(P2-P1)(P/A,i,t2)(P/F,i,t1)+TAX2(P/A,i,t2)(P/F,i,t1)+L2

(13)

式中,右边第一项为企业以BOO模式参与保障性住房项目时政府获得的返还比例现金流现值；第二项为政府租金补偿现值；第三项为企业支付政府税金现值；第四项为企业支付土地成本。

政府的期望收益函数为:

(14)

把式(12)和式(13)带入式(14),引入拉格朗日因子λ2构造拉格朗日函数为:

L(k,λ2)=(P2S-Q-TAX2)k(P/A,i,t2)(P/F,i,t1)-S(P2-P1)(P/A,i,t2)(P/F,i,t1)+TAX2(P/A,i,t2)(P/F,i,t1)+L2+λ2[(P2S-Q-TAX2)(1-k)(P/A,i,t2)(P/F,i,t1)-(I+L2)-(I+L2)R]

(15)

(16)

3.3 采用部分私有化模式参与保障房项目

若企业采用部分私有化模式投资参与保障性住房项目,企业出资比例为r,土地成本、税金和建设成本按照双方出资比例分担,同时收益按出资比例分配,则该模式下企业的投资回报率为:

(17)

由式(17)可见,企业采用部分私有化模式投资参与保障性住房项目的投资收益率与企业出资比例无关。若ROI3>ROI行,则该模式可行。企业采用部分私有化模式参与保障性住房项目时,企业和政府之间为了各自利益仍然存在博弈关系,通过博弈可确定企业的最优出资比例,同时企业收益也需满足要求的收益,即:

NPV3≥(I+L1)×r×R

(18)

NPV3=(P2S-Q-TAX1)r(P/A,i,t2)(P/F,i,t1)-(I+L2)r≥(I+L1)×r×R

(19)

上式化简为:

(P2S-Q-TAX1)(P/A,i,t2)(P/F,i,t1)-(I+L1)≥(I+L1)R

(20)

即必须满足式(20)企业才会参与投资，可见企业是否参与投资与出资比例无关。式(20)左边为企业在部分私有化模式下的净现值,其中第一项为企业收益现值,第二项为企业初始投资额；右边为要求收益。

政府净收益为:

E3=(P2S-Q-TAX1)(1-r)(P/A,i,t2)(P/F,i,t1)-(I+L1)(1-r)-S(P2-P1)(P/A,i,t2)(P/F,i,t1)+rL1+rTAX1(P/A,i,t2)(P/F,i,t1)

(21)

式中,右边第一项为政府收益现值；第二项为政府初始投资额；第三项为政府租金补偿现值；第四项为企业支付土地成本；第五项为企业支付税金现值。

政府期望收益函数为:

(22)

把式(20)和式(21)带入式(22),并引入拉格朗日因子λ3,构造拉格朗日函数为:

L(r,λ3)=(P2S-Q-TAX1)(1-r)(P/A,i,t2)(P/F,i,t1)-(I+L1)(1-r)-S(P2-P1)(P/A,i,t2)(P/F,i,t1)+rL1+rTAX1(P/A,i,t2)(P/F,i,t1)+λ3[(P2S-Q-TAX1)(P/A,i,t2)(P/F,i,t1)-(I+L1)-(I+L1)R]

(23)

从式(23)发现,L(r,λ3)是关于r的减函数。即随着社会资本出资比例增加,政府收益减少,所以政府为获得最大收益,社会资本出资比例最小。由于政府为缓解建造保障性住房项目的资金压力,会给出一个企业最小的出资比例rT,因此可得最优决策出资比例r*为:

r*=rT

(24)

3.4 采用TOT模式参与保障房项目

若企业采用TOT模式参与投资保障性住房项目,设企业购买价格为H,H>I+L1。因为企业未参与建设保障性住房,所以无税金优惠。采用此模式下的特许经营期为t5,期满后政府的剩余经营期为t6。由假设可知,t2=t5+t6,则TOT模式下企业的投资回报率为:

(25)

若ROI4>ROI行,则该此模式可行。企业采用TOT模式参与保障性住房项目也需满足其要求的收益,即:

NPV4≥HR

(26)

NPV4=(P2S-Q-TAX1)(P/A,i,t5)-H≥HR

(27)

式中,左边为企业在TOT模式下的净现值,其中第一项为企业收益现值,第二项为企业购买特许经营权的支付价格。因为在TOT模式下,企业不参与建设保障性住房项目,所以他们的初始投资额为企业购买特许经营权的支付价格;右边为企业要求的收益。

此时政府净收益为:

E4=(P2S-Q-TAX1)(P/A,i,t6)(P/F,i,t5)(P/F,i,t1)+H(P/F,i,t1)-I-L1-S(P2-P1)(P/A,i,t2)(P/F,i,t1)+TAX1(P/A,i,t5)(P/F,i,t1)

(28)

式中,右边第一项为TOT模式下政府经营期的收益现值,第二项为企业购买特许经营权支付价格现值,第三项为项目建设初始投资额,第四项为土地成本,第五项为租金补偿现值,第六项为企业支付税金现值。

政府期望收益函数为:

(29)

把式(27)、式(28)带入式(29),引入拉格朗日因子λ4构造的拉格朗日函数为:

L(t5,λ4)=(P2S-Q-TAX1)(P/A,i,t6)(P/F,i,t5)(P/F,i,t1)+H(P/F,i,t1)-I-L1-S(P2-P1)(P/A,i,t2)(P/F,i,t1)+TAX1(P/A,i,t5)(P/F,i,t1)+λ4[(P2S-Q-TAX1)(P/A,i,t5)-H-HR]

(30)

(31)

3.5 四种PPP模式的投资决策选择

投资回报率的缺点是没有考虑资金的时间价值因素,不能正确反映建设期长短、投资方式不同、回收额有无等条件对项目的影响,用以直接比较四种模式的优劣时缺乏必要的可比性。本文选取等额年金法,考虑了时间因素并改善了投资回报率法的不足。指标值越大,方案越优。等额年金法计算式为:

(32)

四种PPP模式下的等额年金分别为:

(33)

(34)

(35)

(36)

保障性住房项目四种PPP模式的选择为初始投资额不同,项目期不同的互斥方案选择,选用等额年金法考虑了时间因素且能得出可靠的结论。比较四种模式下的等额年金,等额年金越大,方案越优。

4 案例分析

M市拟建立保障性住房项目H,政府自行建设项目时的建设成本为1.8亿元,土地成本为5000万元,项目建设期为2年,项目运营期70年,年末无残值。企业采用PPP模式参与保障性住房项目优惠后的土地成本为3000万元,优惠后需缴纳的税金保持400万元不变；企业采用TOT模式参与保障性住房项目时的特许权支付价格为2.5亿元,企业所得税为25%，折现率为7%,企业要求的利润率为10%,该地区房地产普通住宅长期租赁投资回报率最低为6.1%。若采用部分私有化模式,企业出资比例最低为50%,项目的基本情况构成见表1。

表1 保障性住房项目H基本情况

首先,判断四种PPP模式的可行性与相关最优的投资决策,把相关数据分别代入式(3)和式(9),得到ROI1为11.43%,大于行业最低投资回报率的6.1%,所以BOT模式可行,得出最优投资决策特许经营期为22年;把相关数据带入式(10)和式(16),得到ROI2为8.91%,大于行业最低投资回报率的6.1%,所以BOO模式可行,得出最优投资决策返还的比例为0.22;把相关数据分别代入式(17)和式(24),得出ROI3为9.13%,大于行业最低投资回报率的6.1%,所以部分私有化模式可行,得出最优投资决策投资比例为50%;把相关数据分别代入式(25)和式(31),得出ROI4为8.4%,大于行业最低投资回报率的6.1%,所以TOT模式可行,得出最优投资决策特许经营期为37年;其次,对四种模式进行比较选择,得出最优投资模式。把式(5)和以上计算得出的最优投资决策特许经营期带入式(33)，可得BOT模式下的等额年金NAV1为1970865.47元;式(12)和以上计算得出的最优返还比例带入式(34)可得BOO模式下的等额年金NAV2为1622002.82元;把式(19)和以上计算得出的最优投资比例带入式(35)可得部分私有化模式下的等额年金NAV3为740479.55元;把式(27)和以上计算得出的最优特许经营期带入式(35)可得TOT模式下的等额年金NAV4为1884658.88元。NAV1>NAV4>NAV2>NAV3,可得BOT模式最优，TOT模式次之，BOO模式较差，部分私有化模式最差。因此,保障性住房项目、企业的最优决策为采用BOT模式参与投资,且特许经营期为22年。

5 结论与政策建议

5.1 结论

在博弈论模型下的保障性住房项目PPP模式的投资决策应从政府和企业两方面均衡考虑,选择出政府限制下的最优PPP模式。本文建立了四种PPP模式的投资回报率模型判断PPP模式的可行性,并建立了博弈投资决策模型,判断出企业在政府限制下四种PPP模式的最优决策,考虑了时间价值并全面考虑了项目在整个寿命期的经济状况。此外，采用动态指标等额年金法对四种PPP模式进行了比较优选,为企业参与保障性住房项目建设中PPP模式的选择提供了参考,同时为国家促进企业以PPP模式参与投资保障房项目、制定相应政策提供了有关依据。

通过以上研究，本文得出了以下几条主要结论:一是基于本假设情况下,BOT模式为最优PPP模式。但在实际情况中,企业可能会根据不同的模式选择不同的建设成本和运营成本,进而影响最优模式的选择,不影响选择模型的适用性。二是投资收益率作为效益性指标不能直接应用于多种方案的优选,投资收益率小的方案有可能优于投资收益率大的方案。

5.2 政策建议

综上所述,保障性住房PPP模式是一种可行且有效的融资模式。PPP模式既保证了企业的经济利益,也保证了政府的社会利益。据此,我们提出促进企业以PPP模式投资参与保障性住房项目的政策建议:首先,加大优惠力度。保障性住房项目因其租金低的特点,很难吸引企业进行投资,因此就需政府在其他方面刺激企业进行投资,适当加大优惠力度，如税金优惠、加大政府补贴、延长BOT模式下企业特许经营期期限、减小BOO模式下的资金返还比例、减少土地成本等。其次,合理分担风险。风险是影响企业参与投资保障性住房项目的最重要影响因素之一。政府在与企业合作时应明确风险的承担者和承担情况,并设置合理条款适当规避企业风险,如为企业贷款提供保证等。同时,为了促进企业的积极性,不能将最大风险设置为企业承担,对企业承担损失较大的风险设置上限。第三,完善法律法规。PPP模式引入我国已久,但是相关政策法规仍然不健全,缺少针对PPP有关项目的专项立法,在出现争议时无法可循、无法可依。对企业来说,这无疑增加了风险负担,也加大了企业在项目实施中具体细节上的时间成本。为了改善这种情况,政府应提高立法步伐,对相关条文进行细节完善,为企业以PPP模式参与保障性住房建设奠定法律基础。

[1]邢海峰.“十二五”保障性住房供应体系建设思考[J].现代城市研究,2012,(5)∶8-12.

[2]倪铭娅.六部门鼓励地方运用PPP推进公租房建设[N].中国证券报,2015-05-23(A02).

[3]李秀辉,张世英.PPP：一种新型的项目融资方式[J].中国软科学,2002,(4)∶42-44.

[4]赖丹馨,费方域.公私合作制(PPP)的效率[J].经济学报,2010,(7)∶97-104.

[5]刘志强,郭彩云.基础设施建设项目引入PPP融资方式探讨[J].建筑经济,2005,(6)∶40-42.

[6]邹星昙.浅析我国基础设施建设中PPP模式应用问题[J].商业时代,2009,(24)∶79，60.

[7]周雪峰.保障性住房PPP融资模式研究——以河南为例[J].建筑经济,2015,(1)∶91-94.

[8]刘广平,田礻韦萌,陈立文.保障性住房PPP模式下社会资本投资决策研究[J].管理现代化,2016,(4)∶20-23.

[9]郝生跃,卢玉洁,任旭.“十三五”时期保障性住房建设可持续模式研究[J].经济纵横,2017,(1)∶46-51.

[10]张明宇.PPP模式在英国保障性住房中的应用[J].价值工程,2012,(5)∶328-329.

[11]田礻韦萌,刘广平,陈立文.保障性住房项目PPP模式识别与选择研究[J].管理现代化,2016,(6)∶71-73.

[12]刘广平,张静超,陈立文.公共租赁住房项目PPP模式比选研究[J].项目管理技术,2017,15(2)∶7-13.