A New D－GCL for Unidirectional Motion with Large Displacement

，，

College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China

0 Introduction

Flows around moving boundaries can be encountered in many practical situations，such as aeroelastic problems of aircrafts，stage separation of rockets，separation of projectile and the takeoff and landing of aircrafts，and so on.Generally，there are mainly four kinds of computational fluid dynamic（CFD）methods for moving boundary problems：（1）Grid velocity method［1］，which is to simulate unsteady flows via grid movement；（2）overset grid method［2］，where valid Chimera holes need to be cut in each grid in regions that overlap with solid bodies or any other non－flow regions which belong to the other grids of the overset grid system；（3）moving grid method［3］，which uses arbitrary Lagrangian－Eulerian（ALE）scheme to solve unsteady Euler/Navier－Stokes（N－S）equations；（4）the immersed boundary method［4］，which is becoming apopular approach due to its simplicity and easy implementation.

To avoid the error induced by grid motion，the geometric conservation law （GCL）proposed by Thomas and Lombard［5］，should be taken into consideration.It poses some restrictions on the update procedure for the positions of grid points and grid velocities.Lesoinne and Farhat［6］stated that the change in area（volume）of each control volume betweentnandtn＋1must be equal to the area（volume）swept by the cell boundaries duringΔt＝tn＋1－tn，and they found that spurious and potentially unstable oscillations may occur if GCL was violated.Later，Koobus and Farhat［7］formulated the consequence of GCL on the second－order implicit temporal discretization of the semi－discrete equations，and used it as a guideline to construct a new family of second－order time－ac－curate and geometrically conservative implicit numerical schemes for flow computations on moving grids.They also stated that it had been shown that violating GCL in aeroelastic computations could introduce a parasitic weak instability in the lift response.Therefore，GCL should be satisfied without much increase of computational complexity.From another point of view，Guillard and Farhat［8］proved that satisfying an appropriate DGCL is a sufficient condition for a numerical scheme to guarantee at least first－order time accuracy on moving grids.Further，Farhat et al.［9］pointed out that for sample ALE schemes，satisfying the corresponding D－GCL is a necessary and sufficient condition for a numerical scheme to preserve the nonlinear stability of its fixed grid counterpart，and the impact of this theoretical result was numerically studied through some practical applications.

In general，GCL can be solved explicitly at each control volume face for the boundary velocities［10］，where geometric calculation would be complex and thus more computational efforts are needed.In practice，a more simple and efficient way is to directly evaluate the volume fluxes through all control volume faces，by which complex geometric calculation can be avoided.However，the accumulated error may be produced when using this method and sometimes they could not be ignored，e.g.，in the cases of unidirectional large mesh deformation.Moreover，due to the error，the non－physical negative cell volume may be encountered，causing the program blowing up，yet there is little research about this issue.Hence，a new D－GCL is proposed in this paper which uses the control volume analytically evaluated from the grid motion at the time leveln，instead of using the calculated value from the DGCL itself.By analyzing the truncation error，it is theoretically proven that the accumulated error could be effectively reduced，while without loss of the accuracy of numerical schemes.The capability of the proposed method is numerically demonstrated by adopting a rotating circular cylinder case and a descending GAW－（1）two－element airfoil case.

1 GCL and Original Discrete Procedure

GCL originates from the basic requirement that any ALE schemes should be able to exactly predict the trivial solution of a uniform flow.The ALE equation of mass conservation is usually taken as the starting point to derive the geometric conservation law.For an arbitrary control volume Ωbounded by a closed surface S，the integral form of the law of mass conservation can be written as follows［11］

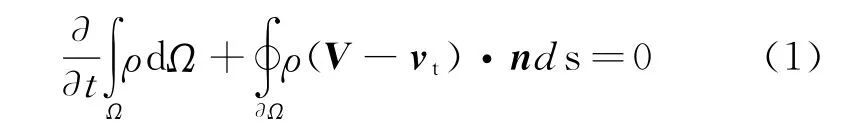
whereρis the fluid density，Vthe fluid velocity，vtthe velocity of the boundary of the control volumeΩ ，and n ＝ （nx，ny，nz）is the unit normal vector pointing outwards of the surface element ds，as shown in Fig.1.

Fig.1 Discretization of the original GCL

With the assumption of a uniform flow having a constant densityρand a constant velocity V ，Eq.（1）turns to in the integral form of the geometric conservation law

Eq.（2）can be temporally discretized by using the same numerical method as used to solve the physical conservation laws.In the case of a first－order time discretization，the corresponding discrete GCL is written as［11］

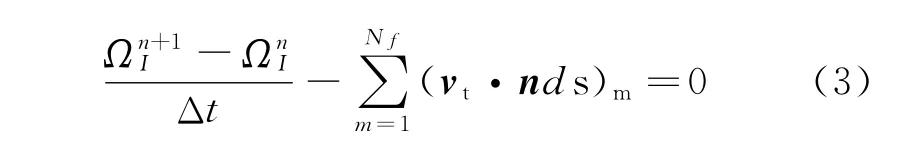
whereNfrepresents the number of control volume faces and the superscripts n and（n＋1）denote the current and the next time levels，respectively.From Eq.（3），we have

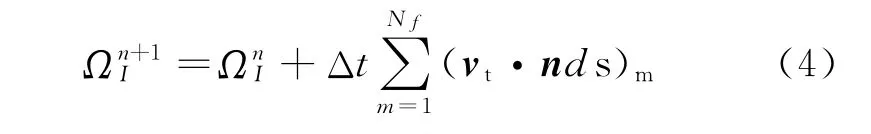
Note that Eq.（4）is an explicit scheme for obtainingΩn＋1I，considering that vtand ncan be analytically evaluated in advance according to the grid motion.

2 New D－GCL and Truncation Error Analysis

2.1 Cumulative error

Theoretically，the volume flux in Eq.（3）equals to zero for such moving control volumes，where the shapes of the grid cells do not change in time.However，the numerical error is inevitably introduced by a spatial discretization method，i.e.

For a reciprocating motion，e.g.the pitching motion of an airfoil，the error can be counteracted by itself.But for a unidirectional motion with large displacements，such as the rotation of a wind turbine and the landing and take－off of an aircraft，the error will be gradually accumulated when Eq.（3）is marched over time.In this case，the continuous accumulation of a negativeεwill probably lead to a negative volume.In other words，the phenomenon of D－GCL′s cumulative error is found out just according to a negative volume.

Fig.2 Schematic of a rotating circular cylinder

Fig.3 Grid zones for the rotating circular cylinder case

One typical example is a rotating circular cylinder as sketched in Fig.2.Fig.3shows the corresponding computational domain，which is divided into two zones：Zone 1rotates rigidly with the circular cylinder，and Zone 2remains stationary.O－type grids are applied to both zones and the grid nodes are equally distributed on the interface of the two zones.For achieving apoint matched sliding mesh，as indicated in Fig.4，the physical time step is carefully chosen so that the inner zone rotates across one grid cell per time step.In Fig.5，the cell volume shows an unphysical increase over time when the original D－GCL is used，which is exactly caused by the cumulative error in a unidirectional rotation case.

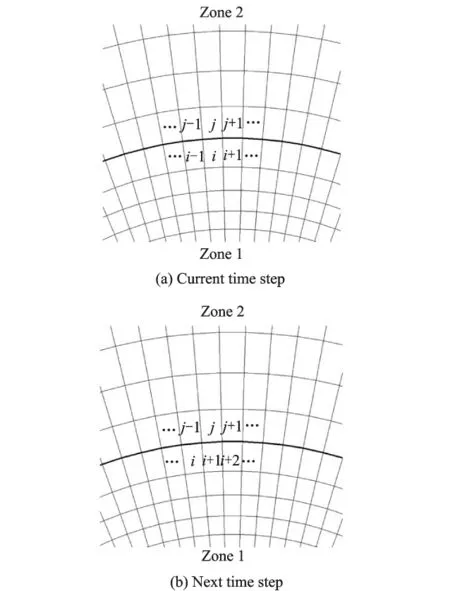
Fig.4 Schematic of point matched sliding mesh

Fig.5 Calculated volumes of cell（1，1）by using the original D－GCL and the proposed D－GCL

2.2 New D－GCL and error analysis

To avoid the cumulative error here，the control volume at the time levelnis analytically evaluated according to the grid motion，instead of using the calculated value from the D－GCL itself.In addition，the normal vector is computed at the midpoint configuration between two neighboring time levels，by which the numerical error of the volume flux computation can be effectively reduced.As a result，a new D－GCL is presented

does not contain any accumulated error of time leveln，and the calculated cell volume is almost constant as shown in Fig.5，according with the real situation.

Here we turn to the analysis of truncation error of numerical schemes with the new D－GCL.Extending Eq.（1）additionally to the laws of momentum and energy conservation by using a firstorder time－accurate scheme，we can have

whereτis the time step，Fthe flux function evaluated by a traditional central difference scheme，gmthe gravity center of the facem，Sm＝nmΔSmthe face vector，andθ＝tfor explicit schemes and θ＝t＋τfor implicit ones.The corresponding local truncation error of control volumeΩIcan be written as

Further，F（ρ（gm，t））is similarly expanded

Eq.（22）indicates that with the developed D－GCL，the truncation error of the given scheme can be guaranteed to be at least first－order timeaccurate.Therefore，it is theoretically proven from the above that the accuracy of numerical scheme can be maintained while the accumulated error is reduced.

3 Results and Discussions

To validate the proposed D－GCL，the unsteady flows around a rotating circular cylinder and the descending GAW－（1）two－element airfoil are investigated.

The unsteady 2－D N－S equations on structured moving grids are solved by a finite volume method and a dual time－stepping scheme.Non－reflecting boundary condition is used in the far field，and the no slip boundary condition is enforced at solid walls.Calculation of the rotating circular cylinder uses the laminar flow model.The Spalart－Allmaras one－equation turbulence model is employed for the simulation of turbulent flows around the GAW－（1）two－element airfoil，since it is suitable for the simulation of flow around a multi－element airfoil［12］.

3.1 Rotating circular cylinder

There are two parameters governing the development of the flow around a rotating circular cylinder.One is the Reynolds number，defined byRe＝ρDU/μ，where D is the diameter of the cylinder，Uthe fluid velocity，andμthe kinematic viscosity.The other is the ratio of rotation speed to rectilinear speeds，defined byα＝ωR/U，where ωis the angular speed andRthe radius of the cylinder.In this case，Reis taken as 200andαas 0.5.The multi－block structured grid is used to discretize the computational domain as described in Section 2.1and a simple dynamic mesh method is adopted.For comparison，the original D－GCL and the proposed method are employed，respectively.

Fig.6shows the time histories of the lift coefficient.The result calculated by the proposed DGCL is in excellent agreement with that in Ref.［13］，where an explicit finite－difference/pseudospectral technique and a new implementation of the Biot－Savart law were used to integrate a velocity/vorticity formulation of the Navier－Stokes equations.On the contrary，the result calculated by the original D－GCL significantly deviates from the other two，which is directly caused by the cumulative error.Therefore，the cumulative error is eliminated and a reasonable result is obtained by using the proposed D－GCL.

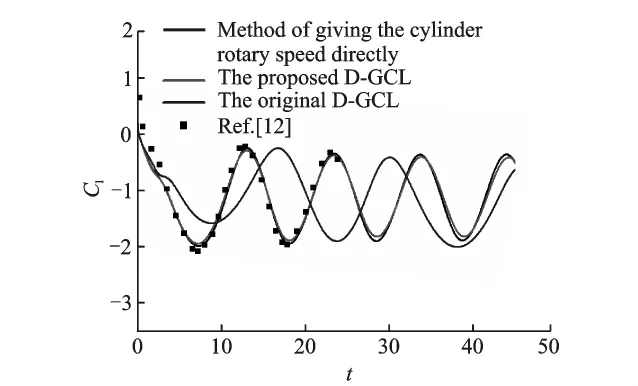
Fig.6 Comparison of calculated time histories of lift coefficient with reference data

3.2 Descending GAW－（1）two－element airfoil

The computation is performed at a freestream Mach number of 0.2，a Reynolds number of 2.2×106and an attack angle of 3.0°.The physical time－step is 1.0×10－3s and the number of the sub－iterations in pseudo time is set as 400.The initial height above ground is 50c.The GAW－（1）two－element airfoil descends at the speed of w0＝3.563 7m/s，and the airfoil′s attack angle is 4.8°.

For this descending airfoil，the strategy of moving grids with local mesh reconstruction as presented in Ref.［14］is adopted.Figs.7，8illustrate the C－H－O－type multi－block grid topology and the local mesh around the airfoil，respectively.The number of grid cells is about 9.3millions.To improve the dynamic mesh quality，during the descending process，Zones from 5to 9move with the airfoil in a purely translational motion，while Zones from 1to 4are deformed by a hybrid RBFs－TFI dynamic mesh method［15］.When the grids become too skewed somewhere，the local mesh reconstruction is then used.

Fig.7 Grid topology of GAW－（1）two－element airfoil

Fig.8 Computational structured grids of GAW－（1）twoelement airfoil

As listed in Table 1，a negative volume is firstly observed at cell（36，18）in Zone 2when any of the original D－GCL，the sophisticated third－order compound Simpson formula in Ref.［16］and the Runge－Kutta method in Ref.［17］is used.However，as demonstrated in Fig.9，the instantaneous dynamic mesh around cell（36，18）is physically very normal，so the calculated negative volume is actually caused by the cumulative error of D－GCL in this large deformation case.Instead，the proposed D－GCL has avoided the numerical problem and predicts a positive and reasonable cell volume.

Table 1 Comparison of calculated cell volumes of Cell（36，18）at t＝13.8s

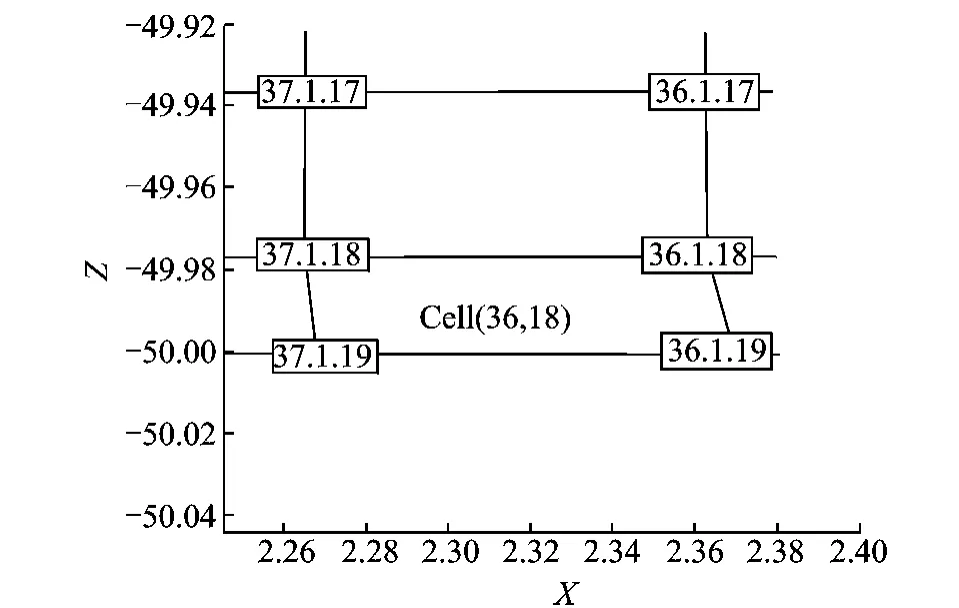
Fig.9 Schematic of the physical grid cell of cell（36，18）in Zone 2

Further，the computed time history of lift coefficient and pressure contour is shown in Figs.10，11，respectively.It is seen that with the proposed D－GCL，the non－physical phenomenon of negative volume does not appear.As the airfoil approaches the ground，the unsteady ground effect has also been investigated.The computation indicates that the lift of the airfoil decreases as it gets close to the ground.Besides，the result is compared with that from the quasi－steady computation，which adds the equivalent attack angle to airfoil′s attack angle.It is found that with the height decreasing，the unsteady ground effect makes the lift first greater than the quasi－steady value and later becomes less after about 13s.

Fig.10 Comparison of calculated time histories of lift coefficient

Fig.11 Pressure contour at t＝13s

4 Conclusions

To eliminate the cumulative error caused by the discrete procedure in the original D－GCL，a new D－GCL is proposed.Error analysis indicates that it can guarantee the truncation error of the numerical scheme at least first－order time－accurate while the accumulated error is reduced.The capability of the method is demonstrated by investigating a rotating circular cylinder case and a descending GAW－（1）two－element airfoil case.The good agreements between the numerical results and the literature data show that the proposed D－GCL can be well applied to unidirectional motions with large displacements.More importantly，the cumulative error is minimized or eliminated and the numerical difficulty of negative cell volume is overcome.

Acknowledgement

This work supported by the National Basic Research Program of China（″973″Project）（No.2014CB046200）.

［1］ PARAMESWARAN V，BAEDER J D.Indicial aerodynamics in compressible flow－direct computational fluid dynamics calculations［J］.Journal of Aircraft，1997，34（1）：131－133.

［2］ NAKAHASHI K，TOGASHI F，SHAROV D.Intergrid－boundary definition method for overset unstructured grid approach［J］.AIAA Journal，2000，38（11）：2077－2084.

［3］ JAHANGIRIAN A，HADIDOOLABI M.Unstructured moving grids for implicit calculation of unsteady compressible viscous flows［J］.Int J Numer Meth Fluids，2005，47：1107－1113.

［4］ PESKIN C S.Flow patterns around heart valves：A numerical method［J］.Journal Computer Physics，1972，2：2252－2271.

［5］ THOMAS P D，LOMBARD C K.Geometric conservation law and its applications to flow computations on moving grids［J］.AIAA Journal，1979，17：1030－1037.

［6］ LESOINNE M，FARHAT C.Geometric conservation laws for flow problems with moving boundaries and deformable meshes，and their impact on aeroelastic computations［J］.Comput Methods Appl Mech Engrg，1996，134：71－90.

［7］ KOOBUS B，FARHAT C.Second－order time－accurate and geometrically conservative implicit schemes for flow computations on unstructured dynamic meshes［J］.Comput Methods Appl Mech Engrg，1999，170：103－129.

［8］ GUILLARD H，FARHAT C.On the significance of the geometric conservation law for flow computations on moving meshes［J］.Comput Methods Appl Mech Engrg，2000，190：1467－1482.

［9］ FARHAT C，GEUZAINE P，Grandmon C.The discrete geometric conservation law and the nonlinear stability of ALE schemes for the solution of flow problems on moving grids［J］.Journal of Computational Physics，2001，174：669－694.

［10］DEMIRDZIC I.Finite volume method for prediction of fluid flow in arbitrarily shaped domains with moving boundaries［J］.International Journal for Numerical Methods in Fluids，1990，10：771－790.

［11］DONEA J，HUERTA A，PONTHOT J P，et al.Arbitrary Lagrangian－Eulerian methods［M］∥ Encyclopedia of Computational Mechanics.［S.l.］：John Wiley＆Sons，Ltd，2004.

［12］RUMSEY C L，YING S X.Prediction of high lift：Review of present CFD capability［J］.Progress in Aerospace Sciences，2002（38）：145－180.

［13］CHEN Y M，OU Y R，PEARLSTEIN A J.Development of the wake behind a circular cylinder impulsively started into rotatory and rectilinear motion［J］.Fluid Mech，1993，253：449－484.

［14］ZHU Yixi，LU Zhiliang，GUO Tongqing.Numerical simulation of multi－element airfoil in unsteady ground effect［J］.Acta Aerodynamic Sinica，2015，33（6）：806－811.（in Chinese）

［15］DING Li，LU Zhiliang，GUO Tongqing.An efficient dynamic mesh generation method for complex multiblock structured grid［J］.Advances in Applied Mathematics and Mechanics，2014，6（1）：120－134.

［16］GERALD C F，WHEAT LEY P O.Applied numerical analysis［M］.Reading Mass：Addison Wesley，1984.

［17］GUO Zheng.Numerical simulation technique research for unsteady multi－body flowfield involving moving boundaries［D］.Changsha：National University of Defense Technology，2002.（in Chinese）