Application of Propagation Characteristics of Translating-Pulsating Source Green Function in the Side-Wall Effects Discrimination
2018-03-28XIAOWenbin
XIAO Wen-bin
(Academy of Ocean Science and Technology,National University of Defense Technology,Changsha 410073,China)
0 Introduction
In the tank with finite breadth,side-wall effects may exert great influence on the ship model advancing in waves,which is mainly due to the reflection waves acting on the model.The waves produced by the model propagate toward the side wall of the tank,and then may go back to it.If there are side-wall effects,many experimental results,such as the motion response,wave excited force,unsteady wave pattern,fluctuating pressure,may be affected.Studies about these effects will contribute to the investigation of hydrodynamic performance difference in the open water and tank condition,and qualitative and quantitative analyses are expected for the side-wall effects in seakeeping model test[1].
For the side-wall effects problem in waves,earlier researches focused on the model test of single ship[2-3].In 1978,15th ITTC proposed standards of seakeeping tests for a single floating body[4].Recently,Ghent University in Belgium and other institutes carried out the model tests of two ships in waves[5-8],but the side-wall effects were still not investigated in depth.In the model tests for two ships advancing parallel in waves,the transversal space in between needs to be adjustable in line with the different experimental conditions.However,the enlargement of transversal space may intensify the side-wall effects,which makes the test more difficult in test design and data analysis.The side-wall effects seem to be more complicated for two advancing models than a single one;the critical wavelength corresponding to each model needs to be considered,besides that,the radiation and diffraction waves generated by a model may act upon the other one.Therefore,the relative position of two models in the tank should be taken into consideration to explore the side-wall effects in regular waves.
In the present paper,the phase function is extracted from the integral representation about 3-D translating-pulsating source Green function in frequency domain,and the stationary phase method is applied to decompose the near-field flow and wave components of the source.Constant phase curves and propagation wave patterns in the far field are then obtained.Based on the propagation characteristics of Bessho form Green function,a simple and practical method is proposed to discriminate the side-wall effects for two ship models advancing in close proximity.Under the experimental conditions,the side-wall effects are examined in a two-model test.
1 Propagation characteristics of Bessho form Green function
1.1 Integral representation
A right-handed equilibrium axis system oxyz is defined in the condition of deep water with the origin o on the plane of undisturbed free surface,and the z-axis is positive upwards.Assuming that the 3-D translating-pulsating source is advancing at a uniform speed U and oscillating at a frequencyis the source point and(x,y, )z is the field point,and then the Bessho form Green function[9]can be written as follows:

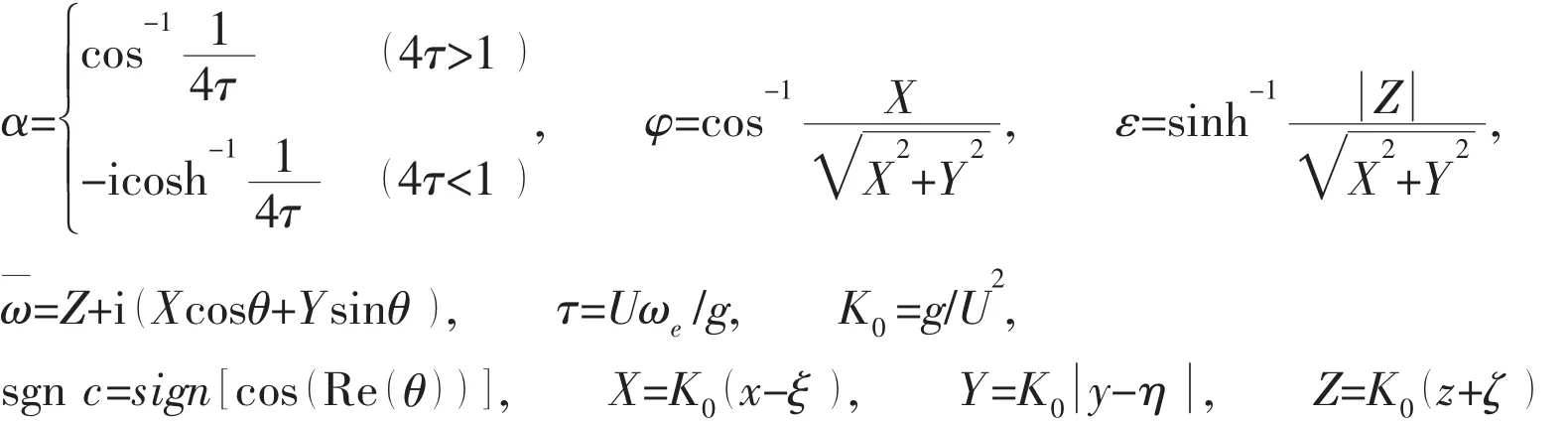
The generalized wave numbers here are represented by k1and k2,and sign is the symbolic function.In terms of the value of τ,the integral path of formula(1)can be divided into two kinds according to the Cauchy integral theorem,which is illustrated in Fig.1.

Fig.1 Integral path of equation(1)in θ space
By performing M=sgn c·m=sgn c·k1cosθ,the terms about k1in formula(1)can be transformed into formula(2)with a single integral form[10].

1.2 Decomposition of near-field flow and wave components
It is known from formula(2),can reflect some nature of exponent part of the exponential function,whose real component represents the oscillation amplitude and imaginary one the phase information.Therefore,the phase function about Bessho form Green function can be defined as

According to the traits of phase function,the wave patterns in far field can be determined by the stationary phase analysis method[11-12].If dψ/dM=0,it is easy to obtain that

By substituting formula(4b)into formula(3),the parametric equation of constant phase curve can then be presented as follows:

The variation range of θ in formula(6)is linked with the integral path in Fig.1.In m plane,the integral path of the new integrand is transformed,which is illustrated in Fig.2 and Fig.3.

Fig.2 The new integral path for terms about k1 in m space
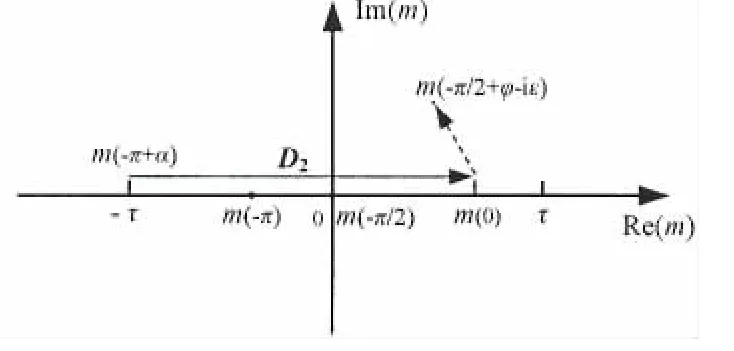
Fig.3 The new integral path for terms about k2 in m space
The imaginary part of variable m is not equal to zero in the intervals identified by dashed lines in Fig.2 and Fig.3.X and Y are,by definition,real numbers,so there is no stationary phase in the corresponding intervals,which means the near-field flow component of the Bessho form Green function is described here.The solid-line intervals in Fig.2 and Fig.3 are divided into three parts including AA,D1and D2,whose contribution is dominant in far field.Therefore,the propagating waves can be determined by equation(5)in the three intervals above.
1.3 Wave patterns in far field
In the water with an infinite free-surface extent,the unsteady waves generated by a translating-pulsating source are closely related to the Strouhal number τ=Uωe/g and its patterns can be indicated by the constant phase curves which represent the wave crests or hollow at a specific time instant[13].Fig.4 shows the propagating wave patterns when the source is located below the origin o.Here X and Y are dimensionless parameters,which can signify the horizontal position between the field point and the source point.
If 4τ<1,there are three distinct wave patterns including outer V wave from AA,inner V wave from D1and ring wave from D2.For the value of 4τ>1,D1and D2are corresponding to inner V wave and ring-fan wave respectively and AA to fan wave.The ring and ring-fan waves above can be considered as the modified ring waves due to the forward speed,and other wave patterns as the modified Kelvin wake due to the harmonic oscillation of the source.All the wave patterns are restricted in the wedge-shaped region which is symmetrical about the advancing course.For the pulsating source,its constant phase curves are circles with the same center and wavelength in all directions[12].By analyzing the wave patterns,the translating-pulsating source seems to be more truly to reflect the propagating waves generated by an advancing ship than the pulsating source dose,which is largely due to the fact that the former source posses special features of forward movement and harmonic oscillation simultaneously.

Fig.4 Constant phase curves of wave patterns when the source is located below o(a)4τ<1;(b)4τ>1

Fig.5 Cusp angle of ring-fan wave pattern

Fig.6 Cusp angle of ring-fan wave pattern versus τ
For the propagating region of the ring wave is the whole free surface area,it is impossible to neglect the side-wall effect when 4τ<1.It is worth noting that the propagating scope of the inner V and fan waves is always within the region of ring-fan wave pattern if 4τ>1.Consequently,the influence area of ring-fan wave can be regarded as the propagating region of the radiation and diffraction waves generated by the translating-pulsating source in the condition of 4τ>1.As shown in Fig.5,a cusp angle θris introduced,which is an angle between the boundary of ring-fan wave and the source course.Fig.6 depicts how this cusp angle changes in dependence of Strouhal number[13].As shown in this figure,the backward spreading feature of ring-fan wave is more and more significant as the advancing speed increases or oscillating frequency decreases,which is consistent with the observed result in physics.In addition,ringfan wave is still possible to emerge ahead of the source when 4τ>1.However,θris always less than 90 degrees if τ>0.272,side-wall effects in which condition is the focus of the present work.
2 Discrimination of side-wall effect for single ship model
In the seakeeping test for single ship,the model is generally set to the central axis of the tank.Fig.7 shows the ship waves reflect from the side walls at different cusp angle θr.Given the tank breadth BTand model length L,it can be easily concluded that there must be a geometric critical cusp angle θtto discriminate the side-wall effect.

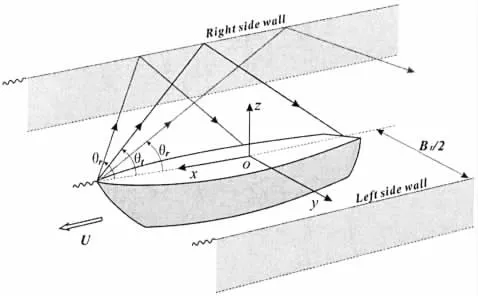
Fig.7 Waves generated by single model and reflected from the side walls of the tank
If θris is larger than θt,the waves generated from the ship stem will act on the flow field at the ship stern nearby after side-wall reflection,and the tank wall interference will occur.If θr<θt,the side-wall effect is absent then.Based on the analysis above,a discrimination method of side-wall effect can be proposed for single ship model.The concrete steps are presented as follows.Firstly,the critical angle θtis solved by tank breadth BTand model length L as formula(7).In terms of the monotone function of cusp angle θrin dependence of τ,the Strouhal number is determined when θtequals to θrin the second step.Thirdly,the corresponding frequency ωeat a certain speed U can be obtained by the definition of τ=Uωe/g.And finally,the critical wavelength λtis achieved with parameters of wave frequency and wavelength.Through comparing the value of experimental wavelength with λt,the side-wall effect can then be identified.The flow diagram of the discrimination method above is illustrated in Fig.8,in which β is the wave-to-course angle with the value of zero in head waves.Input of this method is BT,L,U and propagating property of ring-fan waves.

Fig.8 Flow diagram of discrimination about the side wall effect for single ship model
Based on the tank breadth,model length,speed Froude number and wave circular frequency,15th ITTC recommended a standard for seakeeping experiment of single model in the form of check list[4],whose data essentially indicates the variation laws of the circular Strouhal number τ0=Uω0/g with the ratio BT/L.The relationship between τ0and τ is given in formula(8).

Fig.9(a)and(b)illustrates the discrimination margin of side-wall effect for single model,in which the present results are shown with solid lines.Whichever to adopt to discriminate the effect,τ0or τ,the side-wall effect is not ignorable in the lower left region of the lines and vice versa.In addition,the discrimination data of 15th ITTC is listed in Fig.9(a).By comparison,present results calculated by τ0agree well with the standard data.Therefore,the discrimination method above proves to be correct and effective for single model.It is expected to apply this method to the seakeeping test of two ship models.

Fig.9 Discrimination margin of side wall effect for single ship model
3 Discrimination of side-wall effects for two ship models
In the test of two models advancing in close proximity,the best layout plan is that the two models are arranged symmetrically around the central axis of tank.However,it may strengthen the reforming of towing system for there is only one towing device in universal tank.A simple solution is that one model labeled as ship a is arranged into the carriage navigation system,which is usually located in the central axis of tank.Without loss of generality,another model,labeled as ship b,is set on the starboard side of ship a.The transversal and longitudinal spaces between two models are set as Dyand Dx,respectively,as shown as in Fig.10.If Dy>0,ship b is on the starboard side of ship a.For Dx>0,ship b is ahead of ship a.

Fig.10 Waves generated by two models and reflected from the side walls of tank
The radiation and diffraction waves here are so complex that they need to be analyzed one by one.Taking Fig.10 as an example,the waves generated by the model may reflect back to interfere its own response in waves.In this case,the critical angle can be referenced by the single model.For ship a,this angle θtaais satisfied with formula(9a).For ship b,transversal space Dyis taken into account in the angle θtbbdue to its proximity to the right side wall,which is shown in formula(9b).

where Laand Lbare the lengths of ship a and ship b,respectively.
In addition,the waves from a model may act on the other one after the side-wall reflection.Because of the shadowing effect of ship hull,the interference waves between models’broad sides are restricted in a narrow area,which is an important feature of hydrodynamic interference when two ships are advancing parallel in close proximity.If the two models are not captured,this shadowing effect is not complete in waves[15].And there are radiation and diffraction waves produced by ship a on the starboard of ship b.Here the wave propagation must follow the shortest distance principle from one model to the other.For instance,the wave from ship a is quicker to reach ship b by the right side wall than the left side.So the critical angle θtbais determined by the right side wall as formula(9c).In a similar way,the angle θtabis given in formula(9d).

Above all,the side-wall effects for two models advancing parallel in waves can be discriminated in terms of the four angles as formula(9a)~(9d).And the minimum value of them is defined as θtto determine if the side-wall effects occur.

4 Instance analyses
For the models test of Cheng Kung University in Ref.[16],the discrimination method above is applied to check the side-wall effects.Tab.1 shows the main particulars of the tested models.

Tab.1 Main particulars of tested models
In the test,two models are advancing in head regular waves with the wavelength range 1.93-6.24 m.The principal dimension of the towing tank is 180 m×8 m×3.5 m and speed Froude numbers Fnare 0,0.076 and 0.141.In the experimental condition with Dx=0,two kinds of model layout are discussed here.The first layout is that ship a is set in the central axis of tank and ship b is on the starboard side of ship a with Dy=0.72 m,0.82 m and 0.92 m.No matter how the transversal space changes,two models are arranged symmetrically around the central axis of tank in the other layout.
When Fnequals to 0 or 0.076,side-wall effects occur in both layouts.For Fn=0.141,the critical wavelength appears near 5 m.Fig.11 depicts the wavelength range free of side-wall effect in the experimental conditions.From this figure,the critical wavelength tends to be shorter along with the increase of transversal space.For the transversal space is relative small(Dx/BT=9.0%~11.5%),the change of critical wavelength in accordance with the transversal space is not significant on the whole.

Fig.11 Wavelength range free of side-wall effect(Fn=0.141)
In addition,the wavelength range free of side-wall effect is boarder in the second layout than that in the first one.The symmetrical layout plan,though is more advantageous to avoid the side-wall effect,may enlarge the experimental difficulty and increase the equipment-testing workload.In order to minimize the interference of side-wall effect,the time-history data to be analyzed should be properly intercepted and deep research should focus on its quantitative analysis,which may be the future course of this problem.
5 Conclusions
Based on the propagation characteristics of translating-pulsating source Green function,a practical approach is proposed to discriminate the side-wall effects for single ship model and two models in waves.The main contents and conclusions in present paper are included below:
(1)For the single integral representation about 3-D translating-pulsating source Green function of Bessho form in frequency domain,the parametric equation of constant phase curve is obtained by stationary phase method.The integral intervals of near-field flow and wave components are made clear by the real number property of constant phase curve.If 4τ>1,the propagating area of inner V and fan waves is always within the region of ring-fan wave pattern.And the influence scope of radiation-diffraction waves of the source can be considered as the propagating area of ring-fan wave.
(2)Ring wave and ring-fan wave pattern may emerge ahead of the translating-pulsating source for τ<0.272,and then side-wall effects seem to be not ignored.If τ>0.272,the cusp angle of the source is larger than 90 degrees,therefore it is needed to discriminate the sidewall effects by corresponding method or regulation.
(3)By comparing the ring-fan wave’s cusp angle and geometric critical cusp angle of experimental tank,a discrimination method and its implementing process are presented in the side-wall effect problem for single ship model,and the discrimination margin is obtained by the Strouhal number.Further,a discrimination method of side-wall effects is proposed for two models advancing parallel in regular waves based on the model particulars,tank breadth and relative position of two models,in which the interference of reflection waves acting on both models are taken into account by the shortest distance principle of propagating waves.
(4)The present discrimination method of side-wall effects is not only suitable for the single model and two models test,but also can be applied to the seakeeping test of multihull vehicle and multiple ships.The future work is to further investigate the propagation velocity of the wave patterns,because there is time interval for the propagation waves from the ship to the side wall.
[1]Tasai F,Takaki M,Ohkusu M.Ship motions in restricted waters[J].Journal of the Japan Society of Naval Architects and Ocean Engineers,1978,56:33-45.
[2]Hosoda R.Effects of side-wall interference of towing tank on the results of experiments in waves(1)[J].Journal of the Society of Naval Architects of Japan,1976,139:23-30.
[3]Hosoda R.Effects of side-wall interference of towing tank on the results of experiments in waves(2)[J].Journal of the Society of Naval Architects of Japan,1978,143:52-60.
[4]The Seakeeping Committee of ITTC.Report of the seakeeping committee[C]//Proceedings of the 15th International Towing Tank Conference.Netherlands,1978:55-114.
[5]Vantorre M,Verzhbitskaya E,Laforce E.Model test based formulations of ship-ship interaction forces[J].Ship Technology Research,2002,49(3):1-9.
[6]Evert L,Marc V,Guilaume D.Captive model testing for ship to ship operations[C]//Proceedings of International Conference on Marine Simulation and Ship Maneuverability.Panama,2009:1-10.
[7]Greet V K,Marc V,Guilaume D.Advanced model testing techniques for ship behavior in shallow and confined water[C]//Proceedings of the 1st International Conference on Advanced Model Measurement Technology for the EU Maritime Industry.Nantes,France,2009:158-172.
[8]Zhao W H,Yang J M,Hu Z Q,et al.Recent developments on the hydrodynamics of floating liquid natural gas(FLNG)[J].Ocean Engineering,2011,38:1555-1567.
[9]Bessho M.On the fundamental singularity in the theory of ship motion in a seaway[J].Memoirs of the Defense Academy of Japan,1977,17(8):95-105.
[10]Iwashita H,Ohkusu M.Hydrodynamic forces on a ship moving with forward speed in waves[J].Journal of the Society of Naval Architects of Japan,1989,166:87-109.
[11]Noblesse F,Hendrix D.On the theory of potential flow about a ship advancing in waves[J].Journal of Ship Research,1992,36(1):17-29.
[12]Xu Y,Dong W C,Xiao W B.Study on far field wave patterns and their characteristics of Havelock form Green function[J].China Ocean Engineering,2013,27(3):283-298.
[13]Chen X B,Diebold L.Analytical expressions of unsteady wave patterns[C]//Proceedings of the 14th International Workshop on Water Waves and Floating Bodies.Port Huron,USA,25-28.
[14]Faltinsen O M.Hydrodynamics of high-speed marine vehicles[M].Cambridge University Press,UK,2005:99-140.
[15]Xu Y.Study on the mechanism of hydrodynamic interaction between multiple ships advancing in waves at close proximity[D].Wuhan:Naval University of Engineering,2012.
[16]Yang W H.Experimental verification of the seakeeping performance for two ships advancing parallel in waves[D].Taiwan:National Cheng Kung University,2001.
[17]Mctaggart K,Cumming D,Hsiung C C,et al.Seakeeping of two ships in close proximity[J].Ocean Engineering,2003,30:1051-1063.
杂志排行
船舶力学的其它文章
- Numerical Study of the Shapes of the Super-Rogue Waves
- Hydroelasitic Analysis of the Gravity Cage Subjected to Irregular Waves and Current
- Study on Vulnerability Criteria and Model Experiment for Surf-Riding/Broaching
- LES Simulations of the Flow Around a Propeller in Crash Back and Crash Ahead
- Investigations on the Mechanical Behavior of an Innovative Subsurface Tension Leg Platform in Ultra-Deep Water(Part I)
- Low-Cycle Fatigue Crack-Propagation Behavior of Ship Cracked Plate Considering the Accumulative Plasticity under Variable Amplitude Loading
