变速车道影响下的城市道路多路合流区域换道交通流特性研究
2018-03-28马新露胡月豪何园园
马新露,王 迪,胡月豪,何园园
(重庆交通大学 交通运输学院,重庆 400074)
0 引 言
多条匝道并入主线形成多路合流路段,它已成为城市道路典型的交通瓶颈,极易引发城市路网的“多米洛”和死锁现象。多路合流路段的拥堵源于两点:车道缩减易引发交通阻滞;变速车道设计形式不合理也会扩大瓶颈效应。变速车道原是加速车道、减速车道的总称[1],现指非快速路的城市互通立交中为保证匝道的车辆安全驶入主线而设置的车道。变速车道分为直接式和平行式两种,不同的变速车道引起不同的驾驶行为,诱发交通流呈现不同特征,因此,有必要对变速车道影响下的多路合流路段的交通流特性进行深入探讨。
目前,城市道路的变速车道设计实际采用高速公路加速车道设计方法,并未考虑城市道路交通流特征[2]。国内外学者在此基础上进行改进,主要的方法有宏观的连续流模型[2]、介观的气体动力学模型[3]以及微观的跟驰模型[4],这些方法对微观驾驶行为特性考虑不足,对车道占有率高、驾驶员对合流环境反应敏感的城市道路合流路段并不适用。元胞自动机模型(Cellular Automaton,简称CA)刻画微观驾驶行为特征方面有其独特的优越性,且CA模型能够反映微观驾驶行为与中观交通流特性的相互作用关系。因此,采用CA模型描述城市道路多路合流路段驾驶行为特征,进而探讨变速车道形式与参数对找出交通流特性作用机理具有较高的可行性。
CA模型应用在刻画驾驶行为方面,最原始的元胞自动机交通流模型是S. WOLFRAM等[5]所命名的184号元胞自动机,1992年K. NAGEL等[6]提出了单车道的NaSch模型。李晓白等[7](2001)提出了一个考虑前车速度效应的模型(VE模型)。在单车道的CA模型上引入换道规则,D. CHOWDHURY等[8]提出了经典双车道换道STCA模型。王永明[9]根据道路的阻塞交通流特性,提出了CACF强制换道模型。盛鹏等[10]在此之上建立瓶颈处驾驶员特性的CA模型,刻画了不对称换道和瓶颈抢道行为产生的复杂交通现象。华雪东等[11]引入了反映驾驶心理的换道概率P与安全参数λ,提出了考虑驾驶员换道心理的城市道路双车道换道模型。赵韩涛等[12]在此基础上改进换道规则,建立了城市道路多车道的CA模型。
CA模型在研究变速车道方面,贾斌等[13]研究了合流区通行能力与加速车道长度的关系,发现随着加速车道长度的增加,合流区通行能力增加到一定程度后保持不变。江金胜等[14]基于CA模型得出可通过增加交织区的长度使匝道的交通状况得到显著的改善。刘念琴[15]利用CA模型交织区得出合理的长度值。王琳[16]得到了加速车道长度越长,主线与匝道的通行能力呈先增加后不变的趋势。
CA模型在快速路的主路与一条匝道的合流路段的研究成果较丰富,针对城市道路多路合流交通流的研究不足,涉及主线与匝道、匝道与匝道的交通流作用关系的研究鲜见。同时,对变速车道影响下的多路合流的运行机制的研究不透彻。笔者在已有的成果上,基于实测的换道行为特性,建立城市多路合流路段的CA模型,通过模拟仿真得到变速车道影响下的城市道路多路合流的交通流换道特性,为城市道路多路合流路段的规划、设计与管控提供了理论借鉴。
1 城市道路多路合流换道行为特性
城市道路中的多路合流主要表现为较短纵向距离内的三路合流,选取非快速路的城市三路合流路段为研究对象,如图1,合流路段设有变速车道供匝道车辆汇流,图1(a)的变速车道为直接式,匝道车辆在较短的道路内合流;图1(b)的变速车道为平行式,这种变速车道较直接式的长,设有辅助车道,辅助车道端部设渐变段与主线连接,右侧匝道的车辆经辅助车道或渐变段汇流。
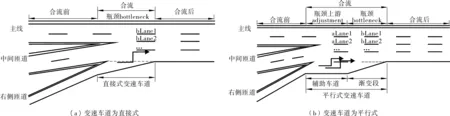
图1 多路合流路段示意Fig. 1 Sketch of multi-road merging region
变速车道的形式与几何参数是影响车辆换道行为的重要因素。其中,换道行为分为自由换道和强制换道[17]。
选取某市3条不同变速车道的三路合流路段为调查对象,来定量分析其对换道行为的影响,其中变速车道路段A、B、C分别为直接式路段、长度较短的平行式变速车道路段和长度较长的平行式变速车道路段。合流路段被分为合流前、合流和合流后3个区域,笔者重点研究受变速车道影响较大的合流区域的交通流特性。直接式变速车道与平行式变速车道的渐变段因车道缩减形成交通瓶颈,故变速车道为直接式的合流区即为瓶颈区,变速车道为平行式的合流区分为瓶颈上游区和瓶颈区,分别用adjustment和bottleneck字符表示,所以路段A、路段B、路段C的瓶颈区分别为A_bottlenck、B_bottleneck和C_bottleneck,路段B、路段C的瓶颈上游区分别为B_adjustment和C_adjustment。若合流区有n条车道,沿交通流方向从左至右,瓶颈区bottleneck的车道分别为bLane1、bLane2、…、bLanen,瓶颈上游区adjustment的车道分别为aLane1、aLane2、…、aLanen。
统计每个区域每条车道的向左自由换道次数NfreeLeft、向右自由换道次数NfreeRight、向左强制换道次数NstrongLeft和向右强制换道次数NstrongRight,计算得到自由换道次数Nfree,Nfree=NfreeLeft+NfreeRight,强制换道次数Nstrong,Nstrong=NstrongLeft+NstrongRight,车道总换道次数Nc,Nc=Nfree+Nstrong;则得到换道概率Pc:Pc=Nc/N;强制换道概率Pstrong:Pstrong=Nstrong/N;自由换道概率Pfree:Pfree=Pc-Pstrong=Nfree/N。
对实测样本分析得到图2的统计结果,其中换道概率由自由换道概率和强制换道概率组成。由图2(a)中的均值与方差分析可得,换道概率均值能反映出3类变速车道形式下驾驶员在瓶颈上游区和瓶颈区的换道意愿强度,而换道概率方差则揭示了换道意愿强度的波动性。
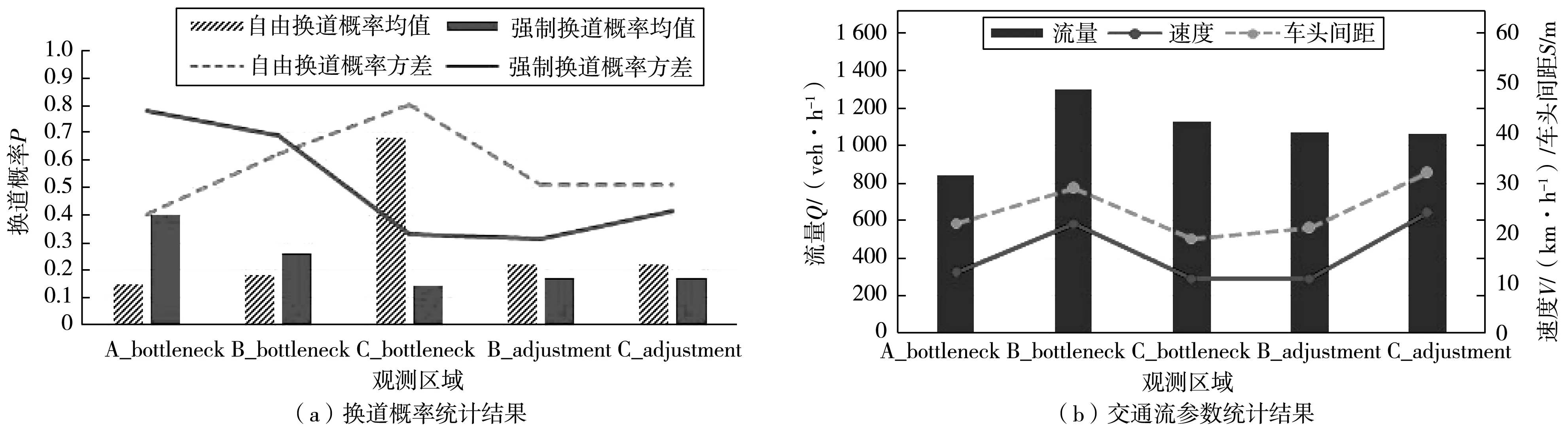
图2 统计参数结果Fig. 2 Statistical parameter results
1.1 瓶颈上游区
统计分析路段B、C的瓶颈上游区adjustment每条车道向左、右的自由换道概率和强制换道概率,得到了各车道向左、右的自由换道概率均值和强制换道概率均值,对应的自由换道与强制换道的占比如图3,B_adjustment中aLane6即为路段B的平行式变速车道,C_adjustment中aLane5即为路段C的平行式变速车道。由图3可知,瓶颈上游区adjustment的换道概率较小;车道从左至右,换道概率递增,高峰期的车道aLane1、aLane2、aLane3有出现车辆排队,车辆为通行向右换道。由图3(b)可知,车辆在C_adjustment的流量、车速大于在B_adjustment的,则车辆在C_adjustment的通行情况优于B_adjustment的,原因如下:
1)C_adjustment的换道概率,尤其是强制换道概率,较B_adjustment的小;C_adjustment的换道与直行的冲突、左强制换道与右强制换道的冲突也较B_adjustment的小,车辆间相互干扰小。
2)进入B_adjustment前,主线、匝道的车辆通行情况较好;由于路段B的变速车道较短,车辆为尽快驶离B_adjustment而多换道,向左和向右的强制换道概率较大,车辆间干扰较大,车辆通行情况较差。
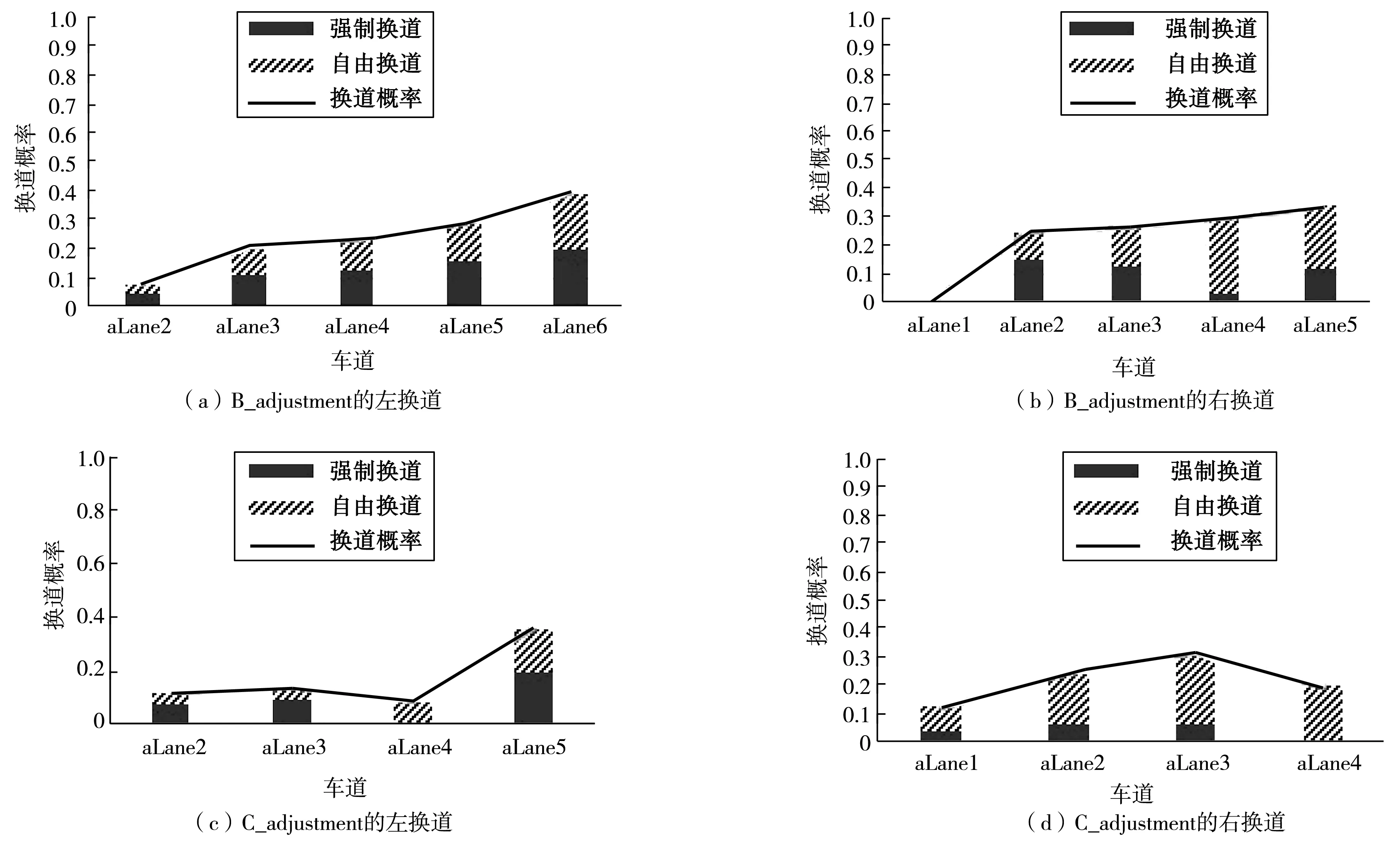
图3 瓶颈上游区adjustment自由换道与强制换道的占比Fig. 3 The histograms of discretionary lane-changing and mandatory lane-changing at traffic bottleneck upstream area(adjustment)
3)因变速车道较长,C_adjustment也较长,进入C_adjustment的车辆多直行,换道以自由换道为主且换道概率较小,车辆间干扰较小,车辆通行情况较好。
1.2 瓶颈区
统计分析路段A、B、C的瓶颈区bottleneck每条车道向左、右的自由换道概率和强制换道概率,得到了各车道向左、向右的自由换道概率均值和强制换道概率均值,对应的自由换道与强制换道的占比如图4,其中A_bottleneck的bLane4对应路段A的直接式变速车道,B_bottleneck中bLane6即为路段B的平行式变速车道,C_bottleneck中bLane5即为路段C的平行式变速车道。

图4 瓶颈区bottleneck自由换道与强制换道的占比Fig. 4 The histograms of discretionary lane-changing and mandatory lane-changing at traffic bottleneck(bottleneck)
2 模型建立
2.1 建模因素
城市道路多路合流路段的驾驶行为复杂,为了使建立的模型更好的反映实际驾驶行为,剖析城市道路多路合流的交通流特性,建模前还需考虑所需其他因素:
1)驾驶员性格:驾驶员由于性格的差异,驾驶行为体现出保守或是冒险的不同特性,建模时需引入描述驾驶员性格的参数[18]。
2)选择换道概率:在换道条件满足时,驾驶员还需抉择换道还是跟驰,为描述这种换道抉择心理,引入了选择换道概率。
3)多车道:实际交通中,城市道路常为多路或多路以上的车道,建立多车道的换道模型[11]。
实测发现,城市道路多路合流的驾驶行为主要为换道与跟驰,换道行为则分为自由换道和强制换道两类[16],而多路合流区的强制换道主要为-挤车换道和末端换道。

2.2 强制换道模型
2.2.1 挤车换道
图5中的“换道车辆”行为属于挤车换道。道路车辆密度较高,车辆行驶速度比较低,当前车遇到前方车辆的停滞阻碍,同时目标车道并不具备良好的换道条件时,会采取强行换道。车辆的这种换道行为会对后方车辆产生影响,为能够安全行驶,这时后方车辆不得不采取减速或停车让行措施。
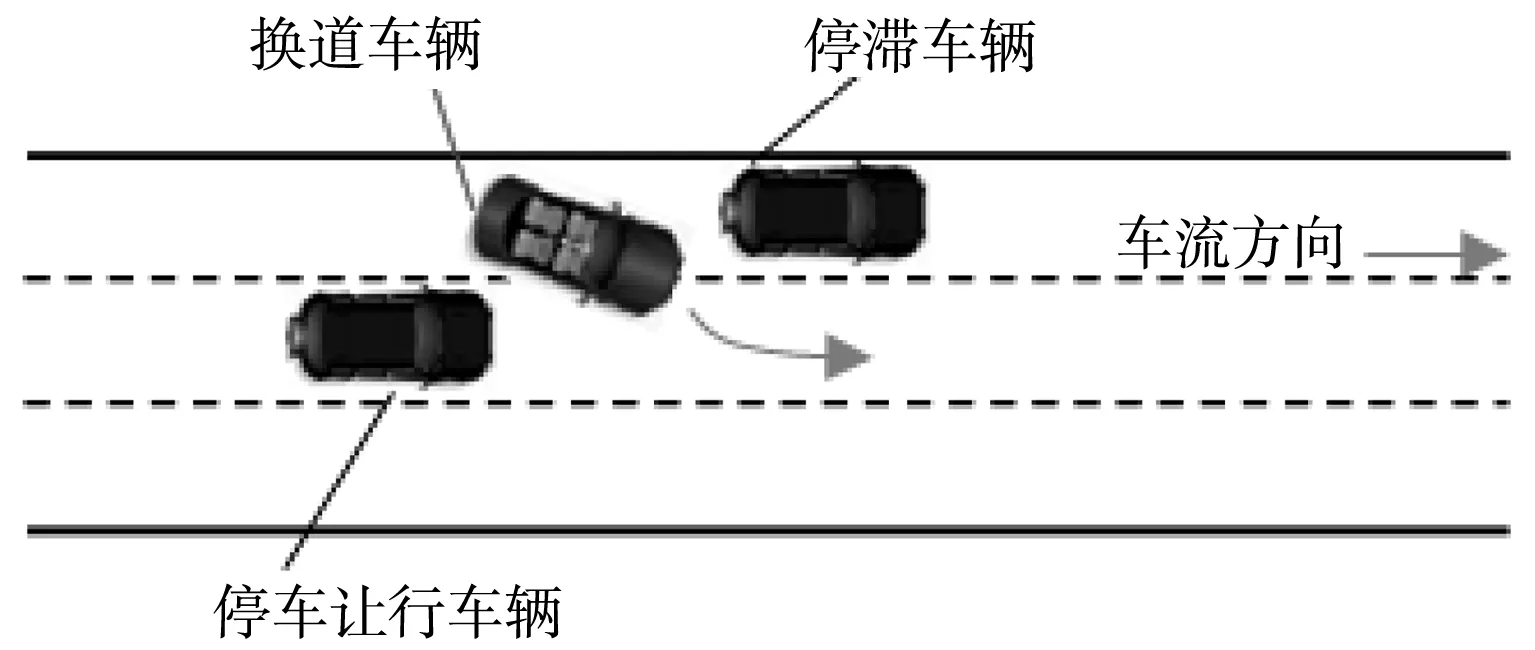
图5 挤车换道示意Fig. 5 Diagram of squeezing the vehicles into the target lane
为描述这类换道行为,改进了原挤车换道模型CACF的挤车换道条件,以驾驶员可忍耐的最大停车时间为参照来设置换道条件[9]。同时,设置选择换道概率P来描述驾驶心理特征表现,得到多路合流的挤车换道模型。
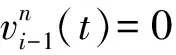
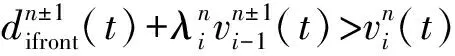

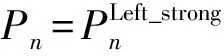
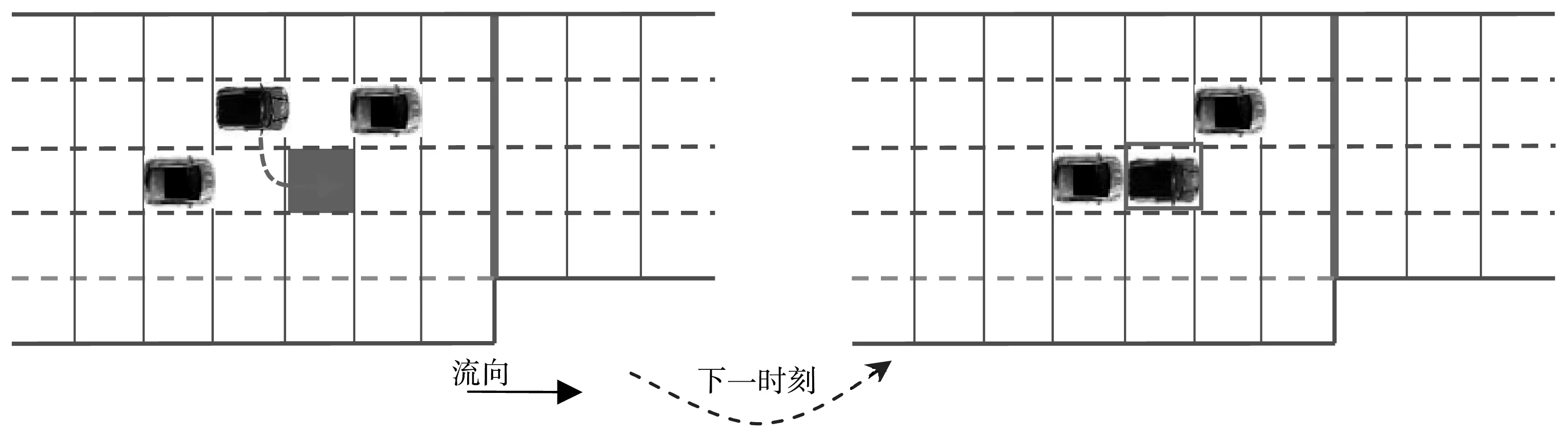
图6 挤车换道建模示意Fig. 6 Modeling diagram of the squeezing the vehicles into the target lane
2.2.2 末端换道
图7中的“换道车辆”,由于道路缩减,变速车道末端的车辆需要换道才能正常行进。车辆末端为了达到通行的目的,无论对其后方车辆是否有影响都会采取换道行为。

图7 末端换道示意Fig. 7 Diagram of terminal lane-changing
为描述多路合流的末端换道行为,建立了考虑车辆间博弈的末端换道模型:
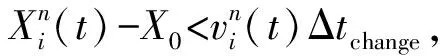


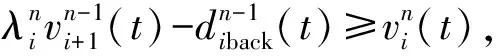
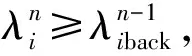
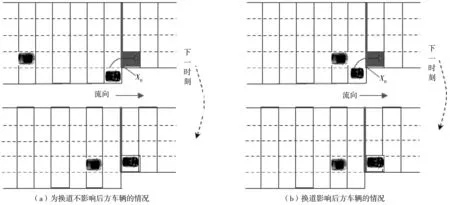
图8 末端换道建模示意Fig. 8 Modeling diagram of terminal lane-changing
2.3 自由换道模型
车辆在原车道不能按照期望速度行驶,而旁道可以提供更好的驾驶空间时,车辆采取的驾驶行为,可以称之为自由换道。在考虑驾驶员性格的基础上,多车道自由换道模型如下:

当车辆同时满足式(1)~式(3)条件就换道:
(1)
(2)
rand() (3) 满足了式(1) ~式(3)的换道条件,车辆换道Gchange(t+1)=1,否则Gchange(t+1)=2,Gchange(t+1)表示欲换道车辆状态,0为停车,1为换道,2为跟驰。 基于驾驶员性格改进了速度效应模型,得到考虑驾驶员性格的跟驰模型。 加速: (4) 减速: (5) 随机慢化: 实际上,直到8月13日,当各路小道消息显示西王集团即将接手山东男篮时,高速男篮俱乐部相关负责人还通过媒体进行了辟谣:假消息,从没听说过此事,也从未跟西王集团有任何接触。 (6) 位置更新: (7) 图9 多路合流模型示意Fig. 9 Modeling diagram of multi-channel confluence 合流后区域有4车道。将优化的CA模型,应用到城市道路多路合流路段的交通流中: 1)合流前和合流后的交通流模型主要有城市道路多路合流路段的跟驰模型和自由换道模型; 2)瓶颈上游区的交通流模型主要为城市道路多路合流路段的跟驰模型、自由换道模型和强制换道模型中的强制换道模型; 3)瓶颈区的交通流模型主要为城市道路多路合流路段的跟驰模型、自由换道模型、强制换道模型和末端换道模型。 由JAVA编写了多路合流的仿真程序,得到了直接式多路合流程序和平行式多路合流程序[20]。 通过数值模拟,研究发现不同变速车道的多路合流路段体现出不同的交通流特征。实验的多路合流路段变速车道选取了长20 m的直接式变速车道,长分别为40、60、90 m的平行式车道。每辆小汽车长度为1个元胞,最大速度vmax为5个元胞。合流区每条车道的元胞数为:平行式的变速车道长度为40、60、90和120 m分别对应的瓶颈区上游每条车道元胞个数为5、9、16和23,瓶颈区车道长为5个元胞;直接式的变速车道长为20 m,其瓶颈区车道长为5个元胞;所有多路合流路段的合流前、合流后的车道长为100个元胞。 数值模拟的边界条件为开放式,运用并行更新规则。模拟将每个时间步分为两个时间子步:第1个时间子步,车辆进行换道;第2个时间子步,车辆根据跟驰规则进行车辆状态的更新[21]。 (8) Kn=m0/m (9) (10) 3.1.1 实测数据验证 图10 仿真换道概率与实测换道概率对比Fig. 10 The comparison between the simulated lane-changing probability and the actually-measured lane-changing probability 根据实测,发现仿真的左强制换道概率数据略小于实测的数据;仿真得到的左自由换道、右自由换道和右强制换道概率与实测换道概率相接近。由此得出仿真结果的有效性,同时也证实了模型的有效性。 3.1.2 模型对比验证 将基于CA模型的城市道路多路合流模型(简称New模型)与经典的合流模型(简述为Old模型)进行对比,验证新模型的优越性。Old模型主要由NS模型与STCA换道模型组成,不考虑驾驶员心理影响因素,且车辆换道条件较为苛刻,只要满足换道条件,车辆即采取换道行为[8]。 仍以路段C的实测数据为参考,New模型与Old模型参数一致,Old模型中没有强制换道概率、选择换道行为和驾驶员性格参数。而New模型的程序参数与3.1.1节的一致。 图11是程序仿真得到的道路时空斑[4],横纵坐标S、T分别表示位移与时间;图中斑点描述车辆的行驶轨迹,图中所示的两个区分别为瓶颈区C_bottleneck和瓶颈上游区C_adjustment。 图11 道路时空斑Fig. 11 Road of spatiotemporal diagram 由图11(a)可见,车辆出入合流区整个过程中的拥挤现象。图11(b)则可呈现合流前道路中出现的不间断停车现象,这是由于NS模型确定性减速条件使得车辆运行较慢,这里采用NS模型描述的城市道路与现实交通显然不符。合流区采用STCA的换道模型,苛刻的换道条件与贪婪的换道机制,频繁的换道致使各车道流量相差较大,产生局部车道排队缓行现象,这与实测交通流现象明显不符。对比图11的道路时空斑图可得,New模型更能反映城市道路多路合流路段的实际驾驶行为。 3.2.1 通行能力分析 通计算右侧匝道、主线和中间匝道的最大流量的平均值,得到了通行能力,对比了40、60、90、120 m的平行式多路合流路段和20 m的直接式多路合流路段的通行能力,如图12。 图12 变速车道影响下的主线与两匝道通行能力对比Fig. 12 The comparison of the traffic capacity between main laneand two-ramp road under the influence of speed-change lane 3.2.2 多路合流交通流影响分析 多路合流交通流影响指主线与中间匝道、中间匝道与右侧匝道之间交通流的影响,可由如图13区域所示的匝道连接区域的车辆换道概率表示,即换道概率越大,换至目标车道的车辆越多,原车道车辆对目标车交通流的影响就越大。 图13 匝道连接区域车辆换道示意Fig. 13 Diagram of vehicle lane-changing at ramp connection area 仿真主线与两匝道流量相等,且分别为600、1 000和1 400 veh/h,得到了匝道连接处20 m内换道概率:主线车辆换至连接中间匝道的车道的概率PMainToMiddle、中间匝道车辆换至主线的概率PMiddleToMain、中间匝道车辆换至变速车道的概率PMiddleToRight、右侧匝道车辆换至连接中间匝道的车道的概率PRightToMiddle,如图14。 图14 匝道连接区域车辆换道概率Fig. 14 Vehicle lane-changing probability at ramp connection area 由图14(a)可见,流量较小时,随着变速车道长度增加,主线车辆换至连接中间匝道的车道的概率PMainToMiddle和中间匝道车辆换至主线的概率PMiddleToMain呈先增后减的趋势,最大值分别为0.375和0.175,L=40 m平行式变速车道对主线和中间匝道的交通流影响较大。中间匝道车辆换至变速车道的概率PMiddleToRight呈递增趋势,变速车道长度越长,中间匝道车辆对右侧匝道交通流影响越大。右侧匝道车辆换至连接中间匝道的车道的概率PRightToMiddle呈递减趋势,其中直接式变速车道L=20 m的PRightToMiddle=1,右侧匝道车辆全都末端换道,对中间匝道交流影响最大。 由图14(b)可见,非自由流时,随着变速车道长度增加,主线车辆换至连接中间匝道的车道的概率PMainToMiddle、PMiddleToMain和PMiddleToRight呈递增趋势,最大值分别为0.335、0.150和0.230,表明主线与中间匝道交通流越易相互影响、中间匝道对右侧匝道交通干扰越大。右侧匝道车辆换至连接中间匝道的车道的概率PRightToMiddle呈递减趋势。 由图14(c)可见,流量较大时,随着变速车道长度增加,主线车辆换至连接中间匝道的车道的概率PMainToMiddle、PMiddleToMain呈递增趋势,最大值分别为0.250和0.200,表明主线与中间匝道交通流越易相互影响。右侧匝道车辆换至连接中间匝道的车道的概率PMiddleToRight=0,除直接式变速车道L=20 m的PRightToMiddle=1,其余PRightToMiddle=0。 综上所述,直接式变速车道的多路合流,右侧匝道车辆对中间匝道交通的影响最大,变速车道越长,其影响越小;变速车道长度越长,中间匝道车辆对右侧匝道车辆干扰越大;随变速车道长度增加,流量较小时,主线与中间匝道的车辆相互影响呈先增后降趋势,在L=40 m时相互影响最大,流量较大时,主线与中间匝道之间车辆干扰越严重。 3.3.1 通行能力分析 在多路合流的数值模拟中,多路合流区的通行能力等于瓶颈区bottleneck[4]。从40、60、90、120 m的平行式多路合流路段和20 m的直接式多路合流路段的通行能力对比中得出,通行能力最大的路段是L=40 m,如图15。瓶颈bottleneck的通行能力受到变速车道的影响,其与变速车道长度成反比关系,统计得到车道长度为120 m时的通行能力为40 m时的70%;直接式与平行式变速车道对瓶颈bottleneck的通行能力影响大小不同,相比之下,瓶颈bottleneck的通行能力降低了20%,直接式变速车道的影响更较大。 图15 变速车道影响下的合流区通行能力对比Fig. 15 Comparison of the traffic capacity of the merging areasunder the influence of speed-change lane 3.3.2 速度分析 收集整理合流区瓶颈流量最大时的速度,再计算获得瓶颈区bottleneck及瓶颈上游区adjustment的平均速度,如图16。 图16 变速车道影响下的合流区速度对比Fig. 16 Comparison of the merge area velocity under the influence ofspeed-change lane 由图16可知,平行式且的多路合流L=40 m时瓶颈区bottleneck达到最大速度,而直接式多路合流的速度最小,后者仅为最大速度的33%。 比较平行式多路合流路段的速度,瓶颈bottleneck的速度与变速车道长度成反比,瓶颈上游区adjustment的速度越大,L=120 m时, bottleneck的速度降低到了47%,adjustment的速度提高了7%。 3.3.3 密度分析 记录瓶颈流量最大时合流区的密度,计算得到瓶颈区bottleneck的平均密度和瓶颈上游区adjustment的平均密度,如图17。 图17 变速车道影响下的合流区密度对比Fig. 17 Comparison of the density of the merging areas under theinfluence of speed-change lane 由图17可知,瓶颈区bottleneck的最小密度是在多路合流为直接式时,其大小仅为最大密度的63%,与瓶颈上游区adjustment两者均在变速车道长度为L=40 m的平行式多路合流产生最大密度。 对比平行式多路合流路段的密度值发现,车道长度越长瓶颈区bottleneck和瓶颈上游区adjustment的密度反而越小,L=120 m时,两者密度较最大值分别减少了21%和47%。 仿真得到的交通流特征参数,证实了实测分析结论:直接式的变速车道会加重交通拥堵;平行式变速车道越长,越不利于车辆通行;长度在40 m左右的范围内,平行式变速车道的多路合流区的通行环境更好。还得到了直接式的变速车道会造成主线与匝道的通行能力降低,而改变平行式变速车道的长度,对主线与匝道的交通影响较小。 针对CA模型在城市道路多路合流路段的交通流建模应用的不足,根据实测的驾驶行为特性和交通流特性,引入了驾驶员性格参数和描述驾驶心理的选择换道概率,建立了基于CA模型的城市道路多路合流的交通流模型,对变速车道影响下的交通流特性研究提供理论支持。 通过改变各项参数运用JAVA模拟了不同情形下多路合流路段变速车道的交通流状况,分析总结了如下的驾驶行为特征及交通流特性: 1)主线与多路匝道的交通流特性。①直接式变速车道不利于主线和多条匝道的车辆通行;主线的通行能力仅为L=40 m的89%,中间匝道的通行能力仅为L=40 m的84%,右侧匝道的通行能力仅为L=40 m的73%;平行式变速车道的长度对主线、多条匝道的通行能力影响较小,变速车道L在40~60 m范围内,车辆通行较好。②变速车道为直接式,右侧匝道车辆对中间匝道交通的影响最大,换道概率为1;相比之下,过长的平行式变速车道,右侧匝道车辆影响骤减,主线与中间匝道之间冲突适得其反,加重中间匝道车辆对右侧匝道的影响。 2)合流区交通流特性。① 直接式变速车道与平行式相比会加剧交通拥挤程度,直接式瓶颈区的车速、密度及通行能力分别是平行式的33%、63%和89%。② 平行式变速车道长度在40~60 m范围内,合流区的交通运行状况良好。③ 过长的平行式变速车道会产生反作用效果,当平行式变速车道长度为L=120 m时,其速度、密度和通行都有不同程度的下降,分别为47%、21%和27%。④产生上述交通现象的因素主要是由于在非自由流时,对于匝道车辆汇流平行式变速车道更具优势,并且在相对较短的合流区域内车辆更趋向于直行,这能减少车辆换道导致的冲突。 笔者通过实测数据分析与模型仿真的方式证明:对交通流量较大的城市多路合流路段,无平行车道的直接式和平行车道过长的平行式变速车道均导致合流区通行效率的下降,变速车道平行段长度在至范围内时合流区通行效率更优,以期为多路合流路段的交通设计与交通组织提供参考。 [1]王莉.高速公路入口匝道结合部通行能力研究[D].长沙:东南大学,2005. WANG Li.ResearchonCapacityofFreewayOn-RampJunction[D]. Changsha: Southeast University, 2005. [2] Transportation Research Board.HighwayCapacityManual[M]. Washington D.C.: Transportation Research Board Publications, 2000: 40-351 [3]李文权,王炜,周荣贵.高速公路合流区1车道车头时距分布特征[J].公路交通科技, 2003, 20(1):114-117. LI Wenquan, WANG Wei, ZHOU Ronggui. Headway characteristics of lane 1 on expressway merge area[J].JournalofHighwayandTransportationResearchandDevelopment, 2003, 20(1): 114-117. [4]张腾.基于VISSIM的长安立交合流区通行能力仿真研究[D].西安:长安大学,2013. ZHANG Teng.ResearchonMergingArea’sCapacityofChang’anInterchangeBasedonVISSIMSimulation[D].Xi’an: Chang’an University, 2013. [5] WOLFRAM S, KADANOFF L P.ANewKindofScience[M].Champaign Illinois: Wolfram Media Inc., 2002: 449-451. [6] NAGEL K, SCHRECKENBERG M. A cellular automaton model for freeway traffic[J].JournalDePhysiqueI, 1992, 2(12):2221-2229. [7] LI X, WU Q, JIANG R. Cellular automaton model considering the velocity effect of a car on the successive car[J].PhysicalReviewEStatisticalNonlinear&SoftMatterPhysics, 2001, 64(6):066128. [8] CHOWDHURY D, WOLF D E, SCHRECKENBERG M. Particle hopping models for two-lane traffic with two kinds of vehicles: Effects of lane-changing rules[J].PhysicalAStatisticalMechanics&ItsApplications, 1997, 235(3/4): 417-439. [9]王永明.基于元胞自动机的道路交通堵塞仿真研究[J].系统仿真学报,2010(9):2149-2154. WANG Yongming. Study of traffic congestion’s simulation based on cellular automaton model[J].JournalofSystemSimulation, 2010(9): 2149-2154. [10]盛鹏,赵树龙,王俊峰,等.基于元胞自动机模型的道路突发瓶颈现象研究[J].物理学报, 2010, 59(6):3831-3840. SHENG Peng, ZHAO Shulong, WANG Junfeng, et al. Study of temporary traffic bottleneck based on cellular automaton model[J].ActaPhysicaSinica, 2010, 59(6):3831-3840. [11]华雪东,王炜,王昊.考虑驾驶心理的城市双车道交通流元胞自动机模型[J].物理学报,2010,60(8):8-9. HUA Xuedong, WANG Wei, WANG Hao. A two-lane cellular automaton traffic flow model with the influence of driving psychology[J].ActaPhysicaSinica, 2010,60(8):8-9. [12]赵韩涛,毛宏燕.有应急车辆影响的多车道交通流元胞自动机模型[J].物理学报, 2013, 62(6):45-52. ZHAO Hantao, MAO Hongyan. Cellular automaton simulation of multi-lane traffic flow including emergency vehicle[J].ActaPhysicaSinica, 2013, 62(6): 45-52. [13]贾斌,高自友,李克平.基于元胞自动机的交通系统建模与模拟[M].北京:科学出版社,2007. JIA Bing, GAO Ziyou, LI Keping.ModelsandSimulationsofTrafficSystemBasedontheTheoryofCellularAutomaton[M]. Beijing: Science Press, 2007. [14]江金胜,董力耘.基于元胞自动机模型的C型交织区交通流特性[J].力学学报, 2012, 44(6):996-1004. JIANG Jinsheng, DONG Liyun. Investigation on traffic flow characteristics around a type c weaving section based on cellular automaton model[J].ChineseJournalofTheoreticalandAppliedMechanics, 2012, 44(6): 996-1004. [15]刘念琴.机场集散枢纽立交交织区的设计优化方法[J].城市道桥与防洪, 2014(5):1-4. LIU Nianqing. Design optimization method of interchange weaving area in airport hub[J].UrbanRoads,Bridges&FloodControl, 2014(5):1-4. [16]王琳.城市道路车辆换道行为特性研究[D].北京:北京交通大学,2015. WANG Lin.TheCharactersResearchofLane-changingBehaviorinUrbanSection[D]. Beijing: Beijing Jiaotong University, 2015 [17]刘立英,李新刚,贾斌.基于元胞自动机模型的交织区通行能力特性分析[J].交通信息与安全, 2013, 31(3):90-91. LIU Liying, LI Xin’gang, JIA Bin. Analysis of capacity of weaving section based on cellular automata model[J].ComputerandCommunications, 2013, 31(3): 90-91. [18]杨紫洁.基于演化博弈的插队驾驶行为研究[D].太原:太原科技大学,2014. YANG Zijie.StudyofQueue-jumpingDrivingBehaviorBasedonEvolutionaryGame[D]. Taiyuan: Taiyuan University of Science and Technology, 2014. [19]张健.考虑细致驾驶行为的双车道交通流建模与控制[D].太原:太原科技大学,2009. ZHANG Jian.ModelingandControlofTwoLaneTrafficFlowwithCarefulDrivingBehavior[D].Taiyuan: Taiyuan University of Science and Technology, 2009. [20]张小琴.基于JAVA技术的网络仿真实验室的设计与实现[J].电脑知识与技术,2011,16(7):4001-4003 ZHANG Xiaoqin. The design and implement of network simulation laboratory based on JAVA[J].ComputerKnowledgeandTechnology, 2011, 16(7): 4001-4003 [21]王永明,周磊山,吕永波.基于元胞自动机交通流模型的车辆换道规则[J].中国公路学报,2008,21(1):89-93. WANG Yongming, ZHOU Leishan, LV Yongbo. Lane changing rules based on cellular automaton traffic flow model[J].ChinaJournalofHighwayandTransport, 2008, 21(1): 89-93. [22]张银.城市道路车道变换微观模型及仿真研究[D].哈尔滨:哈尔滨工业大学,2008. ZHANG Yin.LaneChangeMicroscopicModelandSimulationResearchonUrbanRoad[D]. Harbin: Harbin Institute of Technology, 2008.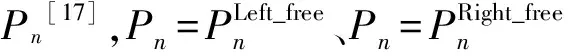
2.4 跟驰模型

2.5 城市道路多路合流路段交通流模型

3 数值模拟



3.1 模型的模拟验证
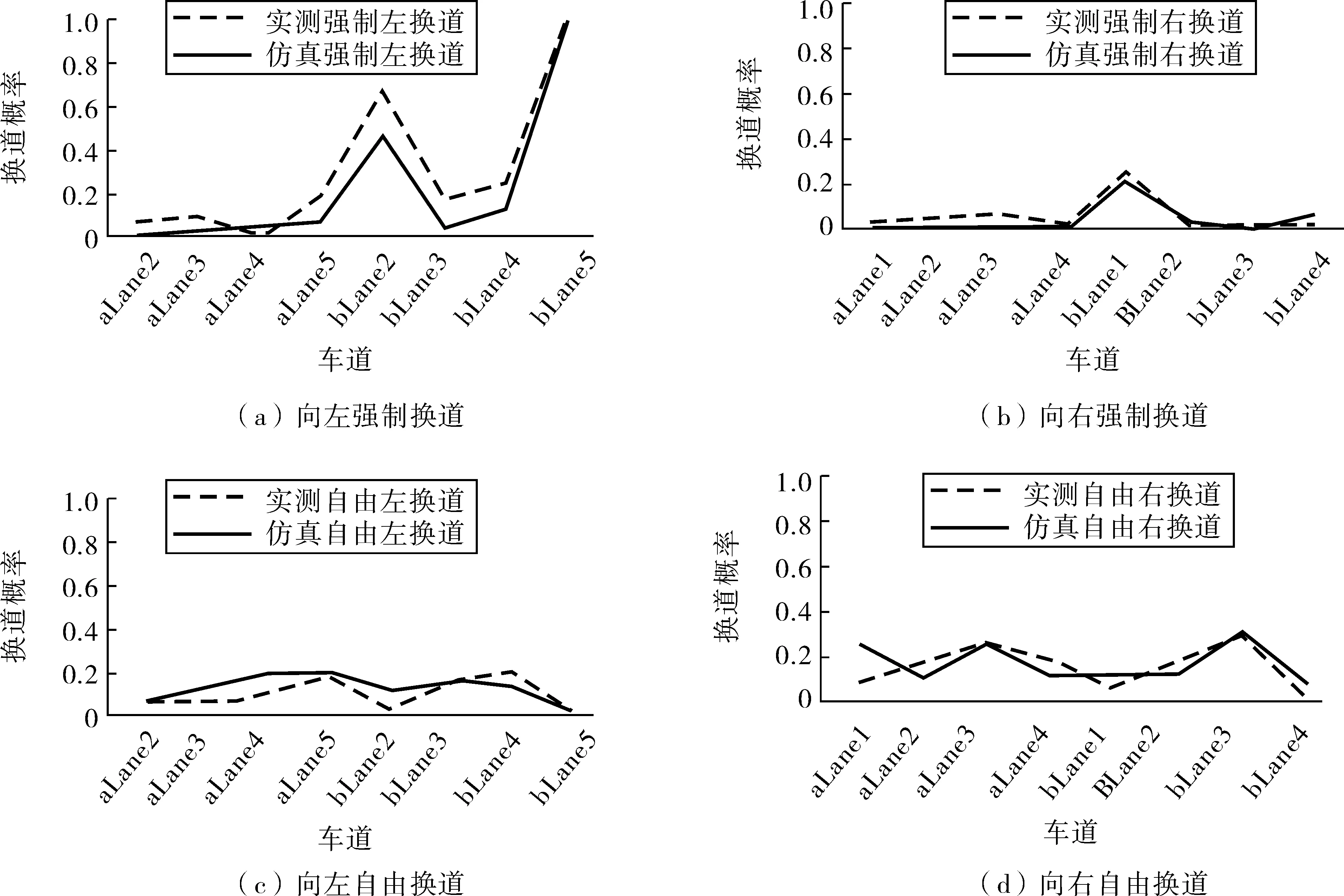
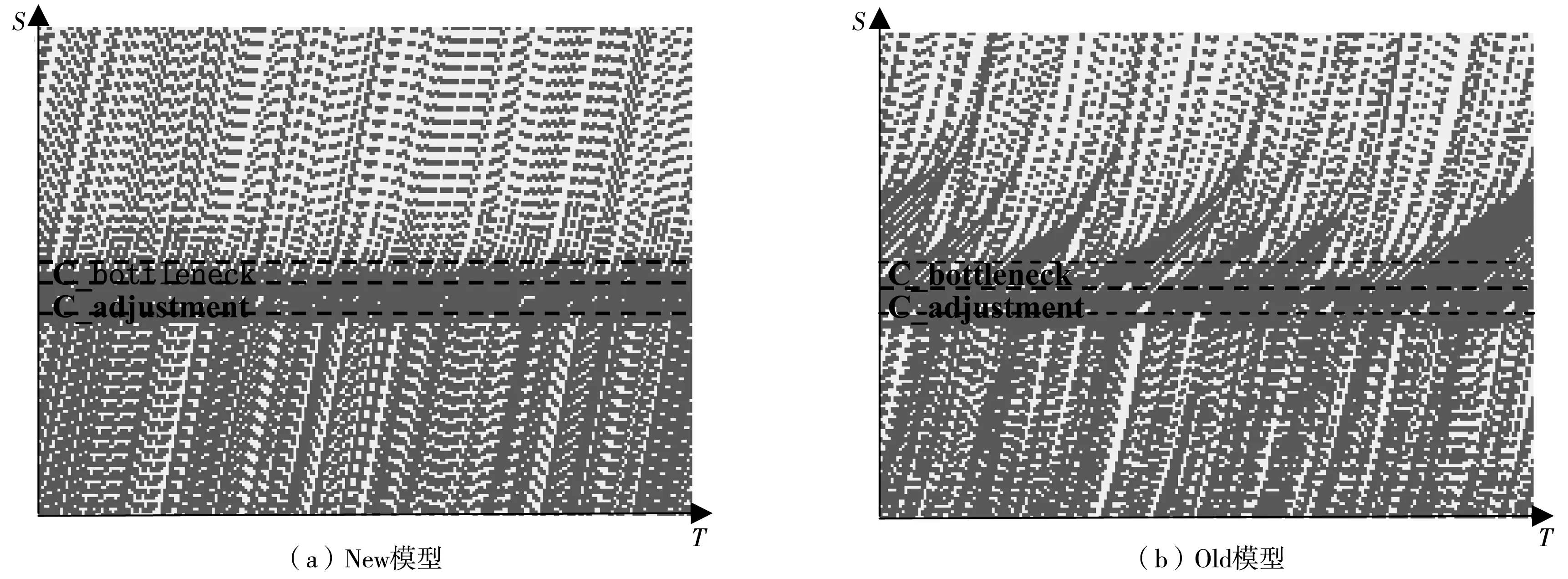
3.2 变速车道主线和多路匝道交通流特性影响
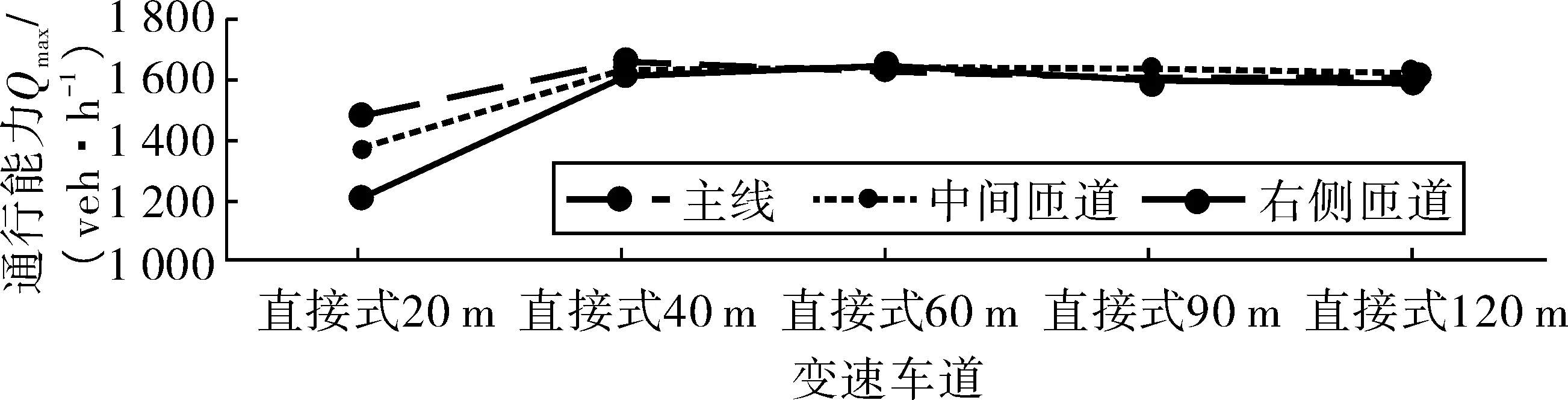



3.3 变速车道对合流区交通流影响


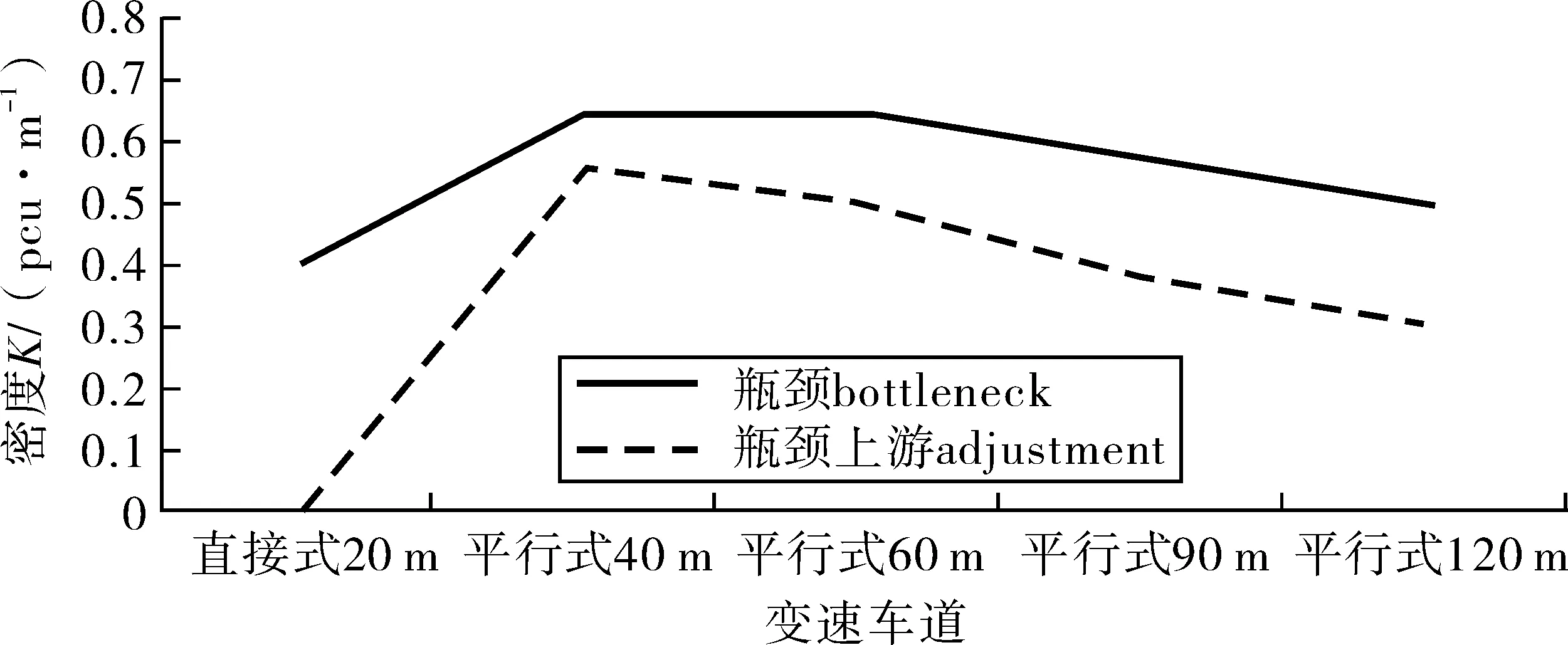
4 结 论
