基于ANSYS的正交异性桥面板焊接动态温度场研究

张 丽

(包头市交通规划设计院，内蒙古 包头 014040)

0 引 言

正交异性桥面板因高承载力、易工厂化、自重轻等优势广泛应用于斜拉桥及悬索桥等大型钢桥设计与制造中[1]。正交异性桥面板各板件的预制连接方式主要采用焊接，焊接过程中不均匀的传热过程导致复杂的塑性形变、相变，形成不均匀的焊接残余应力，降低了结构刚度、承载力及疲劳寿命等，焊接质量直接依赖于动态温度场分布，温度场的计算是获得可靠焊接残余应力场的保证[2]。因而认识焊接热过程的温度动态演变对焊接过程及最终结果的控制具有重要意义。

目前已有较多针对薄板、T形接头等简单结构焊接热过程的温度场数值模拟研究[3-5]，针对正交异性桥面板的多焊缝温度场的准确模拟鲜有报道，笔者拟对某大跨钢斜拉桥的正交异性桥面板动态焊接温度场开展研究并通过试验加以验证，为同类结构焊接热过程的精准控制提供理论参考。

1 焊接温度场的基本理论

基于能量守恒原理可得热传导温度场基本微分方程：

式中：c为材料比热容；ρ为材料密度；λ为材料导热系数，3者均随温度变化；T为温度场分布函数；t为传热时间；Q为内热源。

2 数值模型的建立

2.1 有限元模型

采用通用有限元软件ANSYS对正交异性桥面板的焊接热过程进行数值建模，该计算属于典型三维瞬态非线性过程，矩阵奇异性大，收敛困难，有必要对数值模拟过程进行合理简化[2,6]。考虑到研究对象的对称性，取1.5个U肋的焊接进行分析，几何模型如图1。温度场分析时采用SOLID70热分析单元，由于焊缝处及附近区域为主要受热区域，为降低计算规模提高计算效率，焊缝处采用较密网格，远离焊缝处则增大单元尺寸，两者之间采用过渡网格。有限元模型如图2，节点175 336个，单元134 100个。

图1 几何模型Fig. 1 Geometric model

图2 有限元模型Fig. 2 Finite element model

2.2 焊接工艺

焊接工艺对焊接结果起支配作用，包括实际焊接时的电弧参数及焊接顺序。笔者调查得到实际施焊参数为：焊接电流I为220 A，焊接电压U为26 V，热效率η为75%，焊接速度v为4 mm/s。正交异性桥面板在预制时一般采用交错焊接顺序进行，以降低焊接热变形，焊接顺序见图1。

2.3 物理模型

焊接热过程时的温度场响应依赖于不同温度下的导热系数、密度及比热容等，然而目前材料的高温段热物理特性参数仍旧处于空白状态。笔者参考文献[7]针对Q345钢材的材料参数，如图3，密度按恒定值7 800 kg/m3取值。

U肋与面板的焊缝属于部分熔透焊的范畴，鉴于高斯热源模型仅适合于表面堆焊等工况，笔者采用“双重”生死单元模拟焊缝的填充及热源的移动加载。首先“杀死”焊缝单元，接着参照焊接顺序依次“激活”焊缝单元，并基于生死单元技术及时施加生热率来模拟焊接热源的移动过程，单位时间内生热率为

式中：η为焊接热效率；U、I分别为输入电压、电流；Aw为焊缝截面面积；v为焊接速度。

温度场的边界条件主要表现在结构表面的散热状况，包括对流和辐射两种方式。为简化计算，基于Newton法则，采用统一的换热系数描述其边界约束，边界热损失为

qs=β(T-Tα)

式中：Tα为周围介质温度；β=βc+βE(βc为对流换热系数，βE为辐射换热系数)。

3 温度场结果分析

3.1 温度场瞬时分布

焊接过程中，随着热源的推移，熔池的空间位置不断发生变化，由最初的不稳定态转化为准稳态分布，图4给出了焊接过程中随时间变化的温度分布。

由图4可见，准稳态时的温度场峰值维持在1 976 ℃，热源附近区域的相对温度始终保持固定形态向前推移。温度场呈以焊接方向为对称轴的流星形状，焊接热源前端温度温度梯度较为明显，等温线密集，熔池后方则相对稀疏，梯度并随之变缓。由图4(e)可以看出，焊接顺序对温度场的动态演变有关键影响，由于时间差的存在，后续焊缝区域的温度明显高于先前焊缝区域的温度，但焊接顺序对温度场的最终分布状态并没有显著影响。由于焊接后的冷却时间较长，笔者认为温差控制在1 ℃内即冷却完全。

为进一步探讨正交异性桥面板的温度场分布模式，取桥面板中截面表层路径为研究对象，绘制其25、75、125 s时刻中截面的温度分布曲线，如图5。整体上看，3个时刻的温度场分布趋势基本一致，每个时刻都对应存在一个温度场峰值点，约550 ℃左右，且高温区分布范围较窄，大约局限在焊缝中心两侧各10 mm区间内。值得注意的是，由于施焊顺序的不同，不同时刻温度分布曲线的峰值数量并不一致。在焊接H_2时，由于H_1并未完全冷却，因而对应该焊缝截面处存在一个120 ℃的峰值点。在焊接H_3时，相应的在前两条焊缝对应截面处各存在一个温度峰值，且由于冷却的缘故，相同时间内，H_1焊缝截面处虽有一定的降温幅度，但远小于高温时的降幅速率。

图5 不同时刻下中截面的温度分布规律Fig. 5 Temperature distribution of mid-section at different time

3.2 温度场时间历程变化规律

为了清楚地显示焊接过程中节点热循环动态变化，选择距H_1焊缝中心0、17、30 mm的温度观察点，绘制图6的温度场时间历程曲线。图7则对比分析了三条焊缝中心点温度场时间历程变化规律。

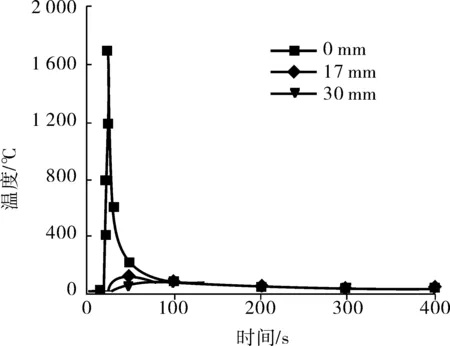
图6 垂直焊缝测点温度时间历程曲线Fig. 6 Time history curve of the temperature of the measuring point of vertical weld

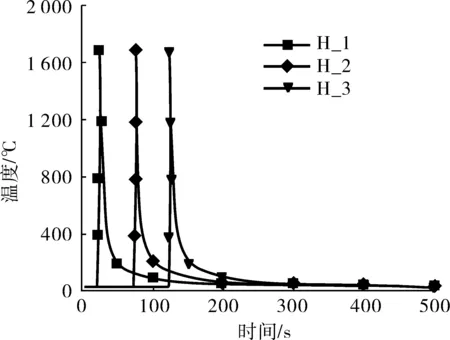
图7 焊缝中心点温度场时间历程曲线Fig. 7 Time history curve of the temperature field at the center point of the weld

由图6可见，随着焊接热源的移动，节点温度经历了室温—峰值—室温的变化历程。在热源作用到某点时，温度急剧上升并瞬速达到峰值，然后节点开始冷却，后方熔池的再热作用使峰值冷却速度略低于加热速度，随着焊件与外界温差越来越小，冷却速率也逐渐开始减慢直至趋于0。温度时间历程的变化趋势与距焊缝的远近无关，但温度峰值、升温及降温速率都有明显下跌，30 mm处的温度变化已经可以忽略，这表明焊接热作用属于局部作用的范畴。

由图7可见，虽然焊缝位置不同，但各中心节点的热循环曲线变化规律基本一致，相对时间内皆按“快升、快降、缓冷却”的模式变化，但各点所受的热作用时刻不同，形成的热影响区性能存在一定差异。

4 数值模拟结果的试验验证

为了验证数值模拟结果的可信度，参考数值模拟中焊接工艺进行实际施焊，并通过热电偶法对焊缝热影响区关键测点的动态温度进行追踪监测，与数值模拟结果进行对比验证，如图8。

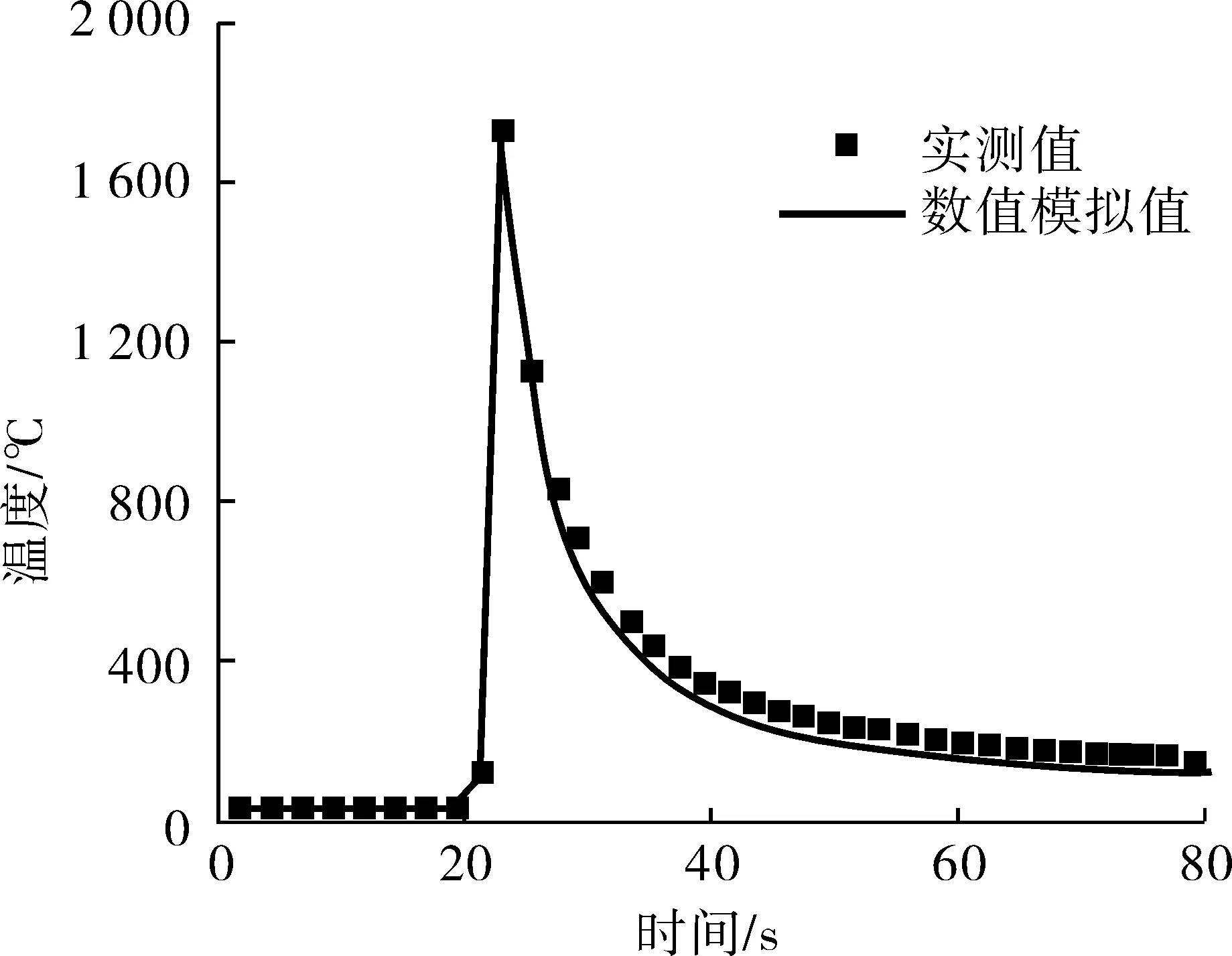
图8 温度实测值与数值模拟值结果验证Fig. 8 Verification of the measured temperature values and numerical simulation results

温度实测值与计算结果整体变化规律基本维持一致，仅在数值上略有偏差，考虑到材料热物理特性的残缺性、模型简化的必要性、测量误差的不可避免性等因素，数值模拟结果与实测数据吻合良好，验证了有限元模拟方法的有效性。

5 结 论

笔者在合理简化焊接热过程的基础上通过ANSYS建立了正交异性桥面板的精细化有限元模型，分析并讨论焊件整体及关键路径的温度场动态分布，得出以下结论：

1)焊接过程的热循环曲线按“快升、快降、缓冷却”的模式变化，温度场呈以焊接方向为对称轴的流星形状，无论是电弧温度还是等温线密集度，熔池前方数值都明显大于后方。

2)焊接顺序显著影响温度场的动态演变，后续焊缝区域的温度明显高于先前焊缝区域的温度，但焊接顺序对温度场的最终分布状态并没有显著影响。

3)U肋各焊缝的温度场规律基本相似，焊接高温区分布范围较窄，大约局限在焊缝中心两侧各10 mm区间内，不同时刻焊件中截面温度分布曲线的峰值数量不一致。

[1]孔祥福,周绪红,狄谨,等.钢箱梁斜拉桥正交异性桥面板的受力性能[J].长安大学学报(自然科学版),2007,27(3):52-56.

KONG Xiangfu, ZHOU Xuhong, DI Jin, et al. Orthotropic deck performance of steel box girder cable stayed bridge[J].JournalofChang’anUniversity(NaturalScienceEdition), 2007, 27(3): 52-56.

[2] D拉达伊.焊件热效应—温度场、残余应力、变形[M].熊京第，郑朝云，史耀武，译.北京:机械工业出版社，1997.

RADAJ D.ThermalEffect-TemperatureFields,ResidualStressandDeformationofWeldComponents[M].XIONG Jingdi, ZHENG Chaoyun, SHI Yaowu, Translated. Beijing: China Machine Press, 1997.

[3]孙盼,李文,姬庆玲.Q235钢焊接温度场的数值模拟[J].中国水运,2010，10(7):235-236.

SUN Pan, LI Wen, JI Qingling. Numerical simulation of welding temperature field of Q235 steel[J].ChinaWaterTransport,2010，10(7): 235-236.

[4]黎超文,王勇,李立英,等.T形接头的焊接温度场三维动态有限元模拟[J].焊接学报,2011,32(8):33-36.

LI Chaowen, WANG Yong, LI Liying, et al. Three-dimensional dynamic FEM simulation of temperature distribution of T-joint[J].TransactionsoftheChinaWeldingInstitution, 2011, 32(8): 33-36.

[5] TSAI C I, FENG Z L. A computational analysis of thermal and mechanical conditions for weld metal solidification cracking[J].WeldingResearchAbroad, 1996, 42(1): 34-41.

[6]朱援详,王勤,赵学荣,等.基于ANSYS平台的焊接残余应力模拟[J].武汉理工大学学报,2004,26(2):69-72.

ZHU Yuanxiang, WANG Qin, ZHAO Xuerong, et al. Simulation of welding residual stress based on ANSYS[J].JournalofWuhanUniversityofTechnology, 2004, 26(2): 69-72.

[7] ANDERSEN L F.ResidualStressesandDeformationsinSteelStructures[D]. Copenhagen: Technical University of Denmark, 2000.