基于深度学习的航空发动机部件故障诊断

, , , ,

(1.海军航空大学 岸防学院,山东 烟台 264001; 2.96917部队,河北 邢台 054100; 3.海军航空大学 航空基础学院,山东 烟台 264001)

航空发动机是由风扇、压气机、燃烧室和涡轮等气路部件组成的复杂机械系统,气路部件的性能对于航空发动机的稳定性具有重要意义。由于气路部件长时间工作在高温、高转速及大应力的恶劣条件下,加上侵蚀、腐蚀以及外来物打伤等问题,因此气路部件容易出现性能衰退故障,从而使发动机的性能受到影响。实现对发动机气路部件故障的识别,可以帮助地勤维护人员发现早期异常,从而达到有针对性地按状态或视情形维修,使维修成本大大降低。

目前,对于航空发动机气路部件的故障诊断方法主要分为基于仿真模型、基于数据和基于知识规则等3类[1]。在很多情况下,由于种种条件的限制,难以获得准确的发动机部件特性,并且不容易建立准确的单机数学模型,因此无法采用基于仿真模型的故障诊断技术。

然而,测量数据容易得到,因此可采用数据驱动方法进行航空发动机的故障诊断。目前数据驱动的故障诊断方法主要有反向传播(BP)神经网络算法、径向基函数(RBF)神经网络算法和支持向量机等。这些方法本质上都属于浅层神经网络算法,存在容易收敛到局部最优或者泛化能力差等问题[2]。因此,基于浅层神经网络算法的发动机故障诊断对于一些复杂故障存在诊断精度不高或容易误诊等问题。

Hinton等[3]提出了深度置信网络(DBN)算法,该算法在图像处理、语音识别和大数据处理[4-6]等方面取得较大进展。

由于深度置信网络算法具有优秀的特征提取能力和学习能力,对数据有更本质的刻画,因此有利于解决分类问题。本文引入深度学习理论进行发动机气路部件故障诊断,以克服传统浅层神经网络算法的不足。

1 深度置信网络

1.1 深度置信网络的特征

深度置信网络是由多个受限玻尔兹曼机(RBM)叠加而成的神经网络结构,如图1所示。RBM2接收底层RBM1的输出作为自己的输入,同时向顶层RBM3输入数据。通过逐层叠加,受限波尔兹曼机对特征进行逐层提取，最顶层的反向传播神经网络则依据抽象得到的特征进行分类。深度置信网络和传统的反向传播神经网络不同,深度置信网络是由随机神经元组成的一种二值型随机网络。随机神经元是指神经元按照一定的概率取值为0或者1,分别对应“关”和“开”2种状态。

深度置信网络算法的训练包括预训练和微调2个阶段。首先,通过无监督训练阶段对每个受限波尔兹曼机进行逐层训练,得到的网络权值和偏置作为初始值;然后,在有监督的训练过程中,利用反向传播神经网络的反向传播算法对整个网络的权值进行微调,以获得更好的网络性能。两阶段训练是深度置信网络算法所特有的,虽然增加了训练的时间,但是可以有效地避免网络陷入局部最优,提高网络收敛的有效性。

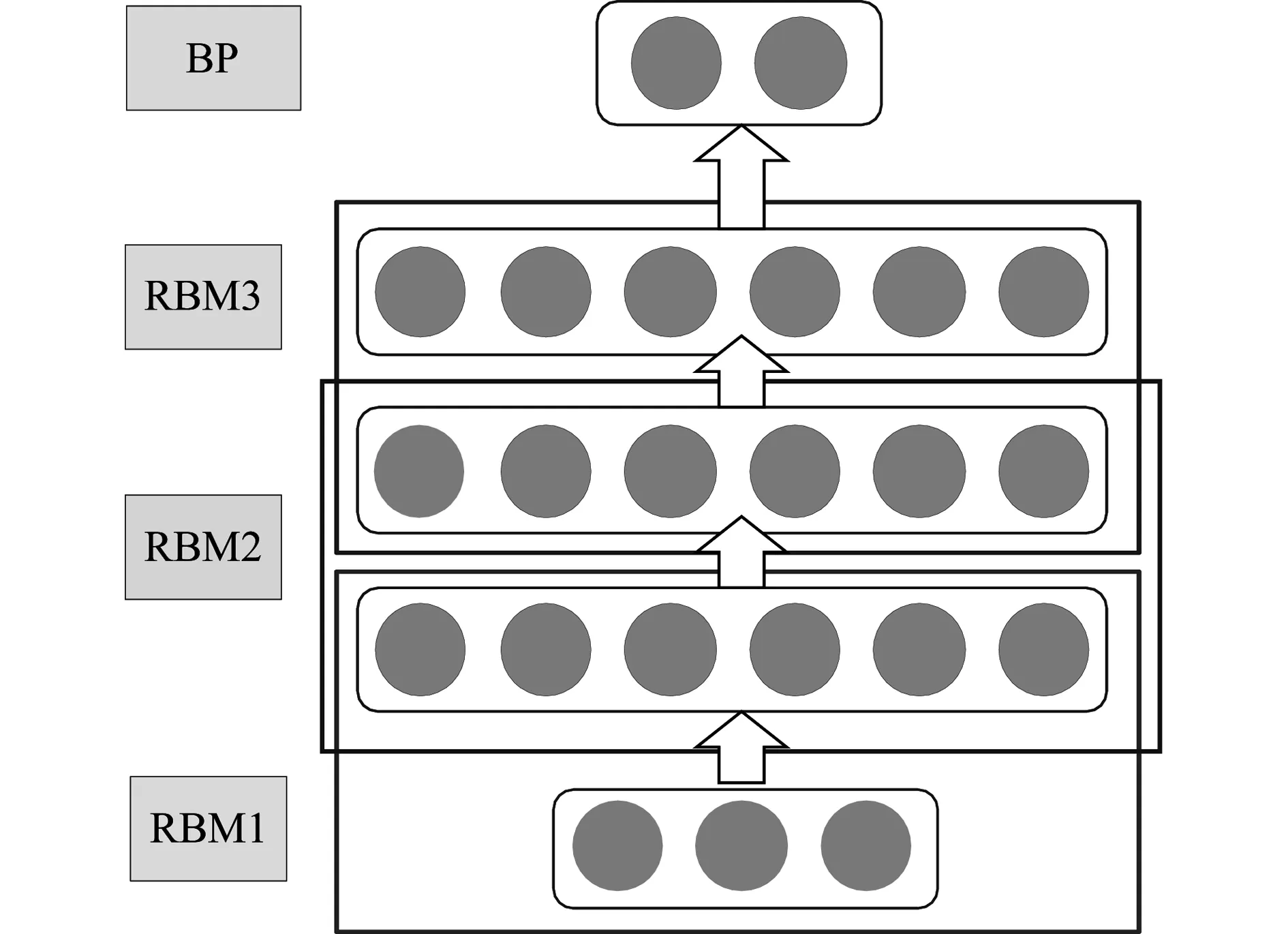
图1 深度置信网络结构Fig.1 Structure of deep belief network

1.2 深度置信网络的训练

受限波尔兹曼模型是由二值随机神经元组成的一个2层结构(见图2),由低层的可见层和顶层的隐含层组成[6]。可见层和隐含层之间的节点相互连接,但是每层网络节点之间不存在网络连接。每个节点只有2个状态,即开和关,取值为{0,1}。

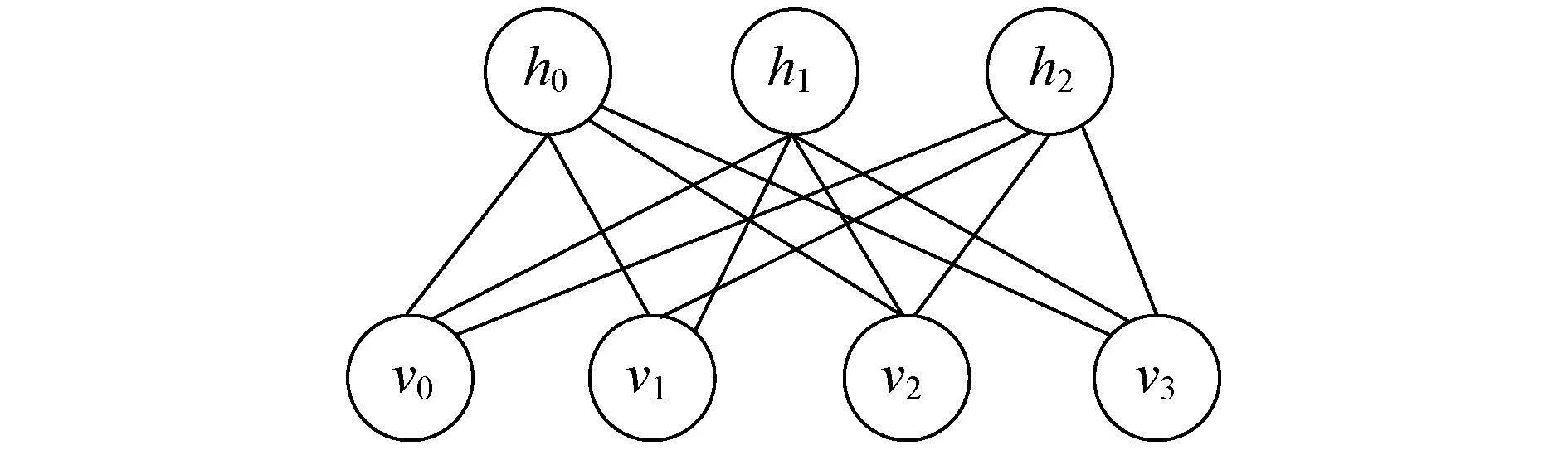
图2 受限玻尔兹曼机的结构Fig.2 Structure of restricted Boltzmann machine

设可见层v=(v1,v2,…,vn),隐含层h=(h1,h2,…,hm),则能量函数定义为

E(v,h)=-avT-bhT-vTWh=

(1)

式中:a为可见层的偏置向量;b为隐含层的偏置向量;W为层间的连接权值矩阵。对于某个受限波尔兹曼机,其2层神经元取当前某一状态所对应的联合概率分布值,由以下公式计算:

(2)

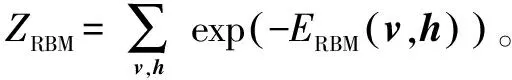
(3)

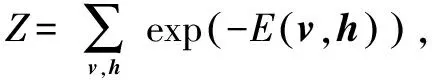
(4)

在给定的可见层节点状态的基础上,隐含层第j个节点hj被激活的概率

(5)

式中:f(x)为激活函数。同理,可求得第i个可见层单元的激活概率

(6)

深度置信网络算法通过极大似然估计方法进行学习,目的在于学习出参数θ(θ={Wij,ai,bi})的值,以拟合给定的训练数据。参数θ可以通过在训练集上(训练样本个数为N)的极大似然函数得到,如下所示:

(7)

式中:L(θ)为参数θ对应的极大似然;k为对应样本编号。

该参数的求解可以用对比散度准则完成。对整个深度置信网络的训练,即第2阶段的“微调”训练,是在每个受限波尔兹曼机完成预训练之后进行的。采用反向传播神经网络的误差反馈传播调整网络各层的权值和偏置,是一种有监督的训练方式。将网络的实际输出结果与标签结果进行对比,利用计算得到的误差对输出层及顶层隐含层之间的权值进行调整;按照同样的方法将误差逐层向下传播,依次调整各隐含层的权值,从而完成整个网络的微调过程。

2 气路部件故障模式设计及样本生成

发动机的长期工作使得发动机部件偏离出厂时的良好状态,导致部件性能出现衰退。气路部件的性能衰退体现在实际流量值和效率值比设计值小,导致发动机整体性能参数发生变化,如发动机排气温度升高或者转子超转[7-8]。

然而,大量真实的发动机故障数据是很难获取的[9]。为了给利用深度置信网络算法进行的故障诊断提供数据,本文采用航空发动机性能模拟软件GSP(gas turbine simulation program)来生成故障数据(见图3),以满足对算法训练和测试的需求。

图3 GSP软件界面Fig.3 Interface of GSP software

本文主要研究10种故障模式,包括风扇的流量衰退、效率衰退、增压比衰退,高压压气机的流量衰退、效率衰退、增压比衰退[8],高压涡轮的流量衰退、效率衰退,低压涡轮的流量衰退、效率衰退。

选择8个发动机工作参数作为网络的输入,如表1所示。

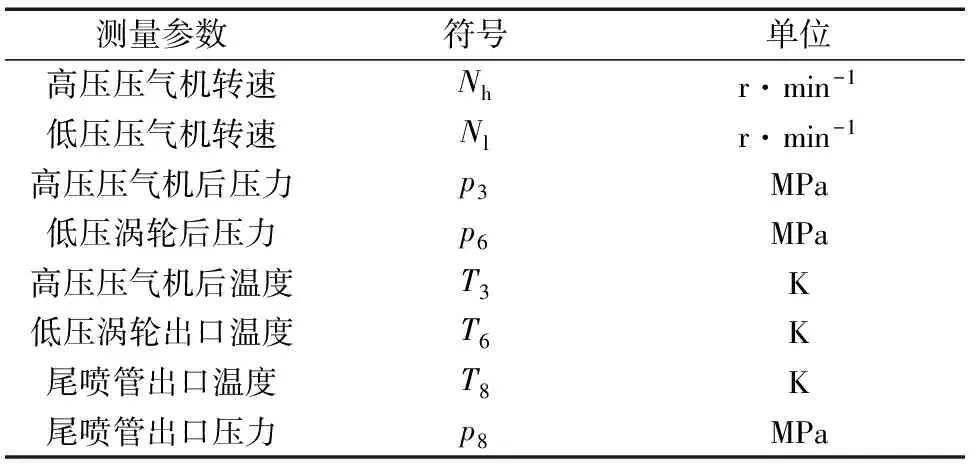
表1 选定测量的参数

选择衰减步长为0.001,在[0.001,0.050]的范围内按步长逐渐减少单个部件性能值,最终计算得到部件性能衰减情况下的发动机工作参数。分别生成如下数据:风扇(低压压气机)流量衰减数据50组,效率衰减数据50组,增压比衰减数据50组;高压压气机的流量衰减数据50组,效率衰减数据50组,增压比衰减数据50组;高压涡轮的流量衰减数据50组,效率衰减数据50组;低压涡轮的流量衰减数据50组,效率衰减数据50组。总共生成500组衰减数据。所有参数在输入网络前均需要进行归一化处理。

3 基于深度置信网络算法的航空发动机部件故障诊断

为了验证深度置信网络算法在发动机气路部件故障诊断方面的有效性,本文选择反向传播和径向基函数2种浅层神经网络算法进行发动机故障诊断的比较研究。

3.1 计算精度的比较

深度置信网络的结构为:输入层的节点有8个;隐含层有2个,每个隐含层由30个神经节点组成;输出层的节点有10个,代表10种故障模式。

深度置信网络所有隐含层的神经元激活函数选择sigmoid函数。在预训练阶段,每一层受限波尔兹曼机训练次数设置为50,微调的反向传播训练次数设置为2 000。

Matlab神经网络工具箱带有反向传播和径向基神经网络函数,为标准化起见,2种浅层神经网络均用工具箱自带函数完成。反向传播神经网络算法分别采用newff( )、train( )和sim( )函数进行反向传播神经网络的构建、训练和拟合。训练函数选择应用较为广泛的trainlm函数,即Levenberg_Marquardt训练算法。最大迭代次数设置为1 000,学习率设置为0.1,训练目标设置为0.000 01。径向基函数神经网络算法采用newrb( )、train( )和sim( )函数进行径向基函数神经网络的构建、训练和拟合。和反向传播神经网络算法不同,采用newrb函数来创建网络是一个不断尝试的过程,需要不断增加隐含层神经元,直到网络误差满足预先设定精度要求或者达到最大神经元个数。本文预设的最大神经元个数为500,误差标为缺省值(0),径向基扩展常数为1.5。

总计有500个故障数据样本,从中选择一部分作为训练样本,剩余的即为测试样本。由于样本选择比例对测试结果有一定影响,因此本文设置了不同的训练样本比例,分别为40%、 60% 、80%。每个训练样本比例情况都重复进行10次计算,以消除训练的随机性。表2为不同训练样本比例下3种算法故障诊断的平均精度。

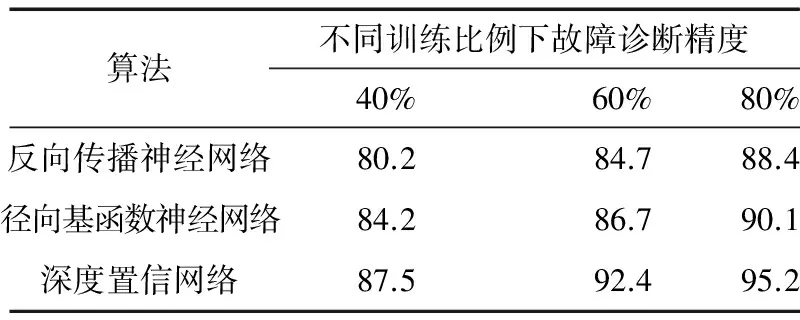
表2 不同训练样本比例下3种算法故障诊断精度比较

由表2可以看出,深度置信网络算法对于发动机故障诊断精度的提高具有很大优势。在3种训练样本比例情况下,深度置信网络算法诊断精度均明显高于反向传播神经网络算法和径向基函数神经网络算法。

图4为训练样本比例80%时深度置信网络算法一次运行结果的混淆矩阵。从图4可以发现,10个类别中有5个类别是100%被正确识别的,其他5个类别各有一个样本被误认为是其他类别,这充分说明了深度学习的诊断有效性。

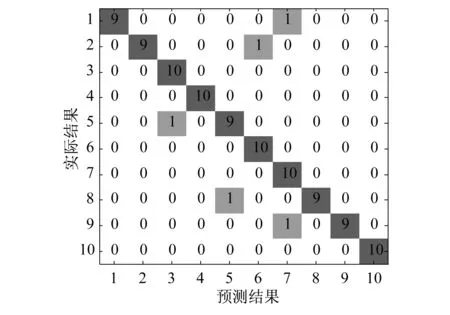
图4 深度置信网络算法故障诊断结果的混淆矩阵Fig.4 Confusion matrix of fault diagnosis results from deep belief network algorithm

3.2 训练时间的比较

表3为3种算法在训练样本比例80%情况下的平均运行时间。

表3 3种算法平均运行时间比较

从表3可以发现,径向基函数神经网络算法的平均运行时间要比其他2种算法都短,主要原因是径向基函数神经网络属于一种局部逼近网络,所以其训练过程运行量要比全局逼近网络少。深度置信网络算法由于包含2个阶段的训练过程,所以其运算消耗的时间要比浅层神经网络算法更长。对于非实时的发动机故障诊断来说,更关注的是诊断精度,较长的训练时间对于非在线应用还是可以接受的。

3.3 抗噪性能的比较

实际的发动机参数在测量过程中往往会被噪声干扰,所以为了更加接近真实情况,在原始数据中加入噪声,如下所示:

Xn=X+Kσrand( )

(8)

式中:Xn为加入噪声后的参数;X为未加入噪声的参数;K为噪声的水平;σ为整个样本的标准差;rand()为[0,1]范围的随机数。分别给样本添加不同水平的噪声(K=0.02,0.04,0.06,0.08,0.10),然后在训练样本比例80%情况下,利用3种算法进行比较。表4为5个不同噪声水平下算法故障诊断精度比较。

表4 不同噪声水平下3种算法故障诊断精度比较

从表4可以发现,随着样本噪声水平的提高,诊断精度都有不同程度下降,但基于深度置信网络算法的诊断精度下降不明显。即使在最大噪声水平下,深度置信网络算法的诊断精度也能在90%以上,抗噪效果较反向传播神经网络算法和径向基函数神经网络算法有显著改善。

4 结语

本文以涡扇发动机为研究对象,利用GSP软件模拟各种气路部件性能衰退故障,进而产生故障样板。深度置信网络算法以及反向传播和径向基函数神经网络算法的故障诊断比较结果表明,深度置信网络算法的精度要明显优于另2种算法,并且在有噪声的情况下仍具有较好的分类性能,这充分说明深度学习在故障诊断领域具有良好的应用前景。需要指出的是,由于深度置信网络结构复杂且参数较多,为获得最优结果,还需要对其结构进行更深入研究。

[1] YANG Xinyi,SHEN Wei,PANG Shan. A novel gas turbine engine health status estimation method using quantum-behaved particle swarm optimization[J].Mathematical Problems in Engineering,2014,11:1-12.

[2] SADOUGH VANINI Z N,KHORASANI K,MESKIN N.Defect detection and isolation of a dual spool gas turbine engine using dynamic neural networks and multiple model approach[J]. Information Sciences,2014,259:234-251.

[3] HINTON G,SALAKHUTDINOV R. Reducing the dimensionality of data with neural networks[J]. Science,2006,313:504-507.

[4] MARKOFF J.Scientists see promise in deep-learning programs[N].The New York Times,2012-11-23.

[5] HINTON G,OSINDERO S,TEH Y.A fast learning algorithm for deep belief nets[J]. Neural Computation,2006,18(7): 1527-1554.

[6] HINTON G E.A practical guide to training restricted Boltzmann machines [J]. Report of Momentum,2010,9(1):1-20.

[7] OGAJI S O T,LI Y G,SAMPATH S,et al. Gas path defect diagnosis of a turb of an engine from transient data using artificial neural networks[C]// 2003 ASME Turbine and Aeroengine Congress.Atlanta:ASME,2003:GT2003-38423.

[8] JAW LINK C.Recent advancements in aircraft engine health management (EHM) technologies and recommendations for the next step[C]// 50th ASME International Gas Turbine & Aeroengine Technical Congress.Atlanta:ASME,2005:683-695.

[9] LEE S-M,ROH T-S,CHOI W-J.Defect diagnostics of SUAV gas turbine engine using hybrid SVM-artificial neural network method[J]. Journal of Mechanical Science and Technology,2009,23:559-568.