塔式起重机结构有限元模型修正的响应面方法
2018-03-28秦仙蓉孙远韬
秦仙蓉, 潘 杰, 徐 俭, 张 氢, 孙远韬
(同济大学 机械与能源工程学院 机械设计及理论研究所,上海 201804)
塔式起重机(塔机)常处于恶劣的工作环境中,因此建立一个经过试验验证的、并能准确反映结构实际状态的有限元模型是进行损伤识别、健康诊断以及工作状态评估与预测的前提条件[1]。然而,由于塔机结构建模过程中的简化以及服役过程中的材料老化和自然灾害等因素的影响,有限元模型计算的响应与现场实测的响应值相比存在一定的偏差,当偏差超过了工程允许的精度时,就必须对有限元模型进行修正[2]。
然而,传统的直接基于结构有限元模型进行修正的方法需要进行逐步迭代计算,每次迭代都需要对参数修改后的有限元模型进行重新计算,称为重分析。在结构复杂、有限元模型自由度数多时,计算量巨大,同时修正效率较低,很难满足实际工程的要求。采用基于响应面方法(Response Surface Method)的有限元模型修正可以克服以上传统结构有限元模型修正的不足,通过统计理论和模型修正技术的结合,得到能反映结构响应与修正参数之间复杂隐式函数关系的显式响应面模型[3],再利用响应面模型进行修正,这样就将计算工作量巨大的有限元分析转移到了计算速度更快的响应面分析,大大提高了修正计算效率。
利用响应面方法实现结构有限元模型修正是近年来的研究热点。任伟新等[4]利用环境振动试验结果,得到结构模态数据以及响应面模型,实现了六跨连续梁桥的有限元模型修正;邓苗毅等[5]提出了基于静力响应面的结构有限元模型修正方法,并利用了两跨连续梁结构验证了所提出方法的有效性;宗周红等[6]提出了基于健康监测的响应面模型修正方法,实现了桥梁结构的高阶响应面模型修正,并应用于模型确认及结构损伤识别领域。Shan等[7]以某斜拉悬索桥为例,将桥梁位移和模态频率同时作为修正目标,实现了基于响应面法的桥梁结构静动力联合修正。Zhou等[8]利用高斯径向基函数响应面实现了理论模型、实验室桥梁模型以及东营大桥的模型修正,结果验证了该方法的高效性与可行性。
本文根据现场实测的塔机模态频率,采用响应面方法实现塔机结构的有限元模型修正。以悬臂梁和QTZ125型塔机为例,分别构建二次多项式与高斯径向基函数两种响应面模型,并利用构建的响应面函数替代有限元模型,实现悬臂梁和塔机结构的有限元模型修正。
1 基于响应面法的有限元模型修正
基于响应面法的有限元模型修正步骤如图1所示,其修正效率和精度主要取决于试验设计、参数筛选及响应面函数形式的选择和拟合三个方面。
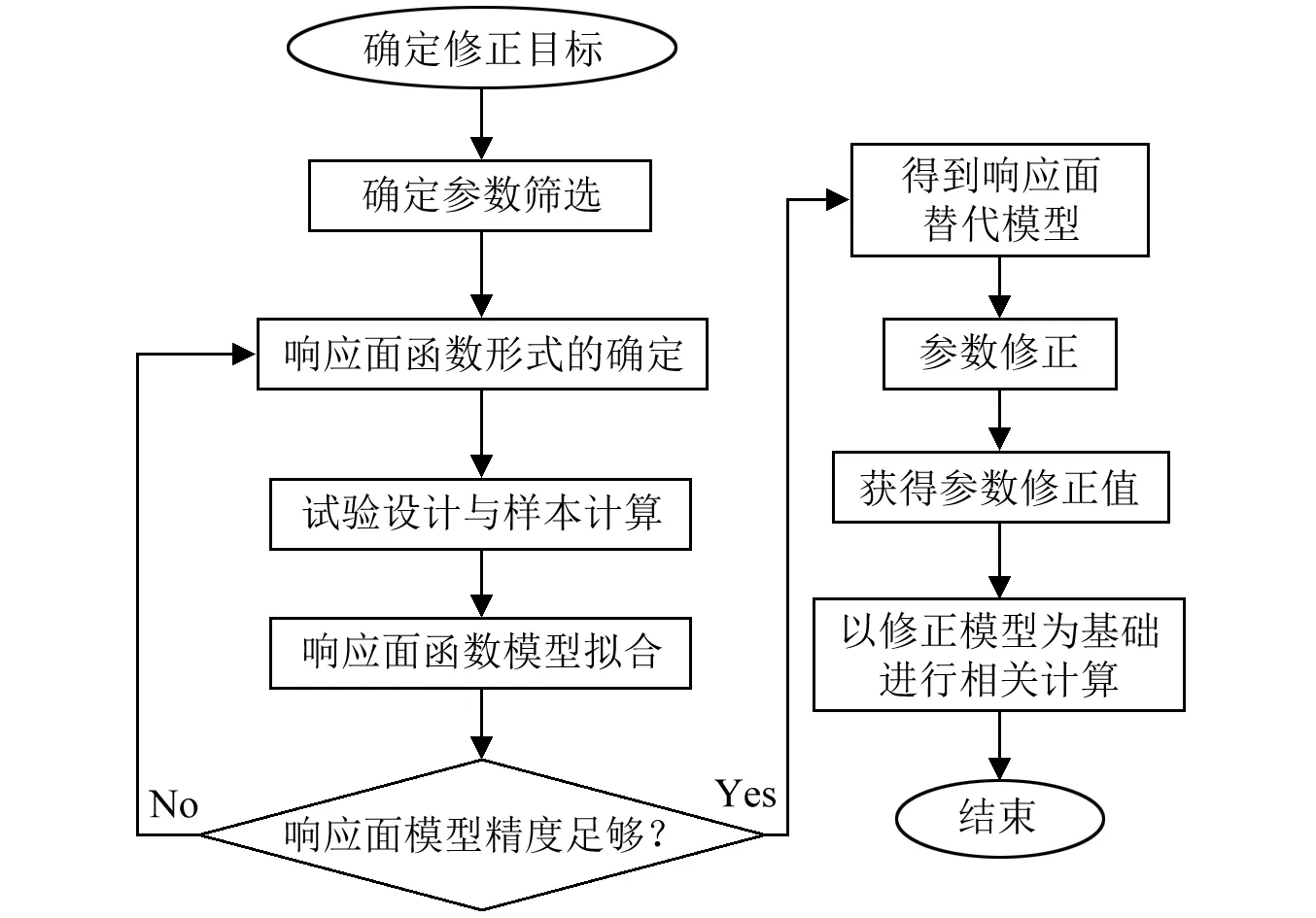
图1 基于响应面法的有限元模型修正流程Fig.1 Finite element model updating process based on response surface method
1.1 试验设计方法
响应面方法常用的试验设计方法有全因子设计法、中心复合设计[9]、D-最优设计、正交设计[10]和均匀设计[11]等。本文选取均匀设计方法,该方法只考虑试验点在试验范围内均匀散布,挑选试验代表点的出发点是“均匀分散”,而不考虑“整齐可比”,它可保证试验点具有均匀分布的统计特征,可使每个因素的每个水平做一次且仅做一次试验。
1.2 待修正参数的选取
本文在待修正参数的选取上,首先利用经验选择方法,选取在工程实际中容易发生变化且对结构响应有较大影响的参数,然后通过灵敏度分析来确定待修正参数。以选取的待修正参数构建初步的响应面模型,采用以F检验法为标准的逐步回归法对响应面的各参数进行显著性分析,从响应面模型中剔除那些对响应不显著的参数。
1.3 响应面函数的选取
目前,二次多项式[12]、BP神经网络、高斯径向基函数[13]、Kriging模型和支持向量机是比较常用的响应面模型。本文将通过具体的数值算例以及工程实例说明二次多项式响应面以及高斯径向基函数响应面在修正过程中的应用与比较。
利用F检验法分析待修正参数对特征频率的显著性时,计算各参数对统计特征量的显著性水平P值,发现交叉项对于模型的显著性较参数的主效应小很多,在不影响精度的情况下,为提高计算效率,本文采用不考虑交叉项的不完全二次多项式响应面
(1)
式中:待定系数β0、β1i和β2i分别为响应面模型的常数项、一次项和二次项系数,响应面系数可由最小二乘法拟合得到;ε为响应面模型的误差。对于不考虑交叉项的二次多项式,待定系数的个数为s=2n+1,其中的n代表设计变量个数。
高斯函数指某种沿径向对称的标量函数,通常定义为空间中任意一点x到某一中心ci的欧氏距离的单调函数,具有形式简单、不依赖于空间维数的优点。高斯函数的表达式为
(2)
式中:r=‖x-ci‖;ci为核函数中心(高斯核);σi为核函数的宽度参数,控制基函数径向作用范围。
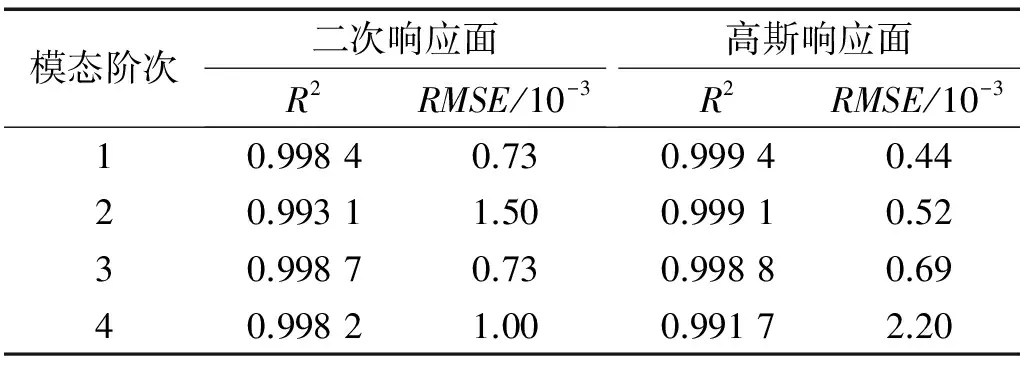
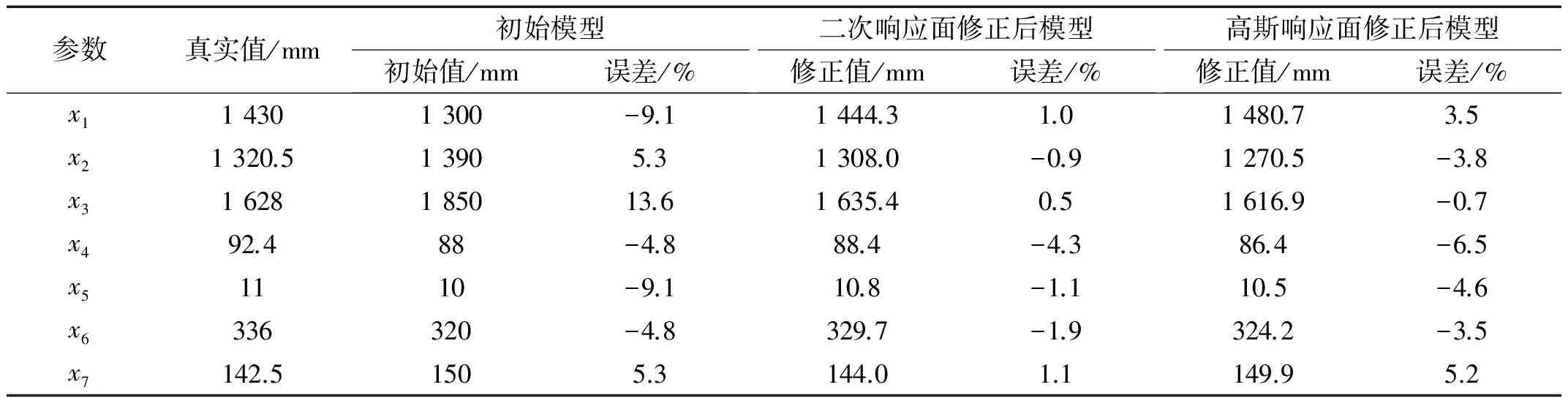
假设被拟合的问题有m个样本(每个样本中有n个设计变量)和b个插值基点(b (3) 式中:j=1,2,3,…,m;wi为第i个插值基点对应的回归系数;xi为第i个插值基点;x∈Rn,xi∈X,X是Rn空间内的有限离散点集。 本文采用相对均方根误差RMSE和决定系数R2检验来评价响应面模型的有效性 (4) (5) (6) 本文联合ANSYS和MATLAB两种商用平台,利用“内点法”实现对优化目标函数式(6)的求解,获得优化后的参数值。 图2为一Euler-Bernoulli悬臂梁,梁总长3 m,横截面尺寸为0.25 m×0.15 m,弹性模量为32 GPa,质量密度为2 500 kg/m3,有限元建模时,将悬臂梁划分为10个单元,得到的有限元模型如图2所示。 图2 悬臂梁有限元模型示意图 (单位:m)Fig.2 Finite element model of a cantilever beam (unit: m) 为了使参与模型修正的参数具有物理意义且有代表性,构建如下“真值模型”。“真值模型”中单元1的高度h1是理论高度的85%,单元2的高度h2是理论高度的115%,其他设计参数与理论参数相同。 图3 悬臂梁各阶模态频率对结构参数的灵敏度Fig.3 Sensitivity of the cantilever beam’s modal frequencies to structural parameters 分组设计变量/m频率/Hzx1x2f1f2f3f410.801.068.4855.55159.54292.8520.860.868.3856.96162.10290.1930.931.209.7558.95164.39300.7241.001.009.6360.16167.72298.4551.060.808.8760.36170.58293.7061.131.1310.6863.52172.88305.2271.200.9310.0863.44175.89301.45 基于表1所示的均匀设计中的样本,分别用二次多项式响应面和高斯响应面拟合悬臂梁模态频率与两个设计变量之间显式的函数关系。采用以F检验法为标准的逐步回归法对各自变量进行显著性分析,得到回归后的二次响应面函数如式(7)~式(10)所示,高斯响应面函数如式(11)~式(14)所示。 二次响应面 7.90(x1)2-7.09(x2)2 (7) 15.66(x1)2-11.18(x2)2 (8) 0.43(x1)2-5.95(x2)2 (9) 29.37(x1)2-27.7(x2)2 (10) 高斯响应面 15.35a(‖x-x6‖) (11) 54.5a(‖x-x6‖) (12) 113.1a(‖x-x6‖) (13) 182.9a(‖x-x6‖) (14) 拟合的响应面的有效性通过相对均方根误差RMSE和决定系数R2评价,其评价结果如表2所示。由表中结果可以发现,两种响应面的RMSE都接近0,同时R2都接近1,表明拟合的响应面在参数的设计空间内,可以作为原有限元模型的替代模型。 表2 悬臂梁二次多项式和高斯响应面模型有效性评价 将悬臂梁前四阶模态频率的响应面模型替代原有限元模型进行优化迭代。表3给出了“真值模型”、初始有限元模型、基于不同响应面修正后的有限元模型计算得出的悬臂梁前四阶模态频率。可以发现:悬臂梁初始有限元模型的模态频率与“真值模型”之间有较大误差,而应用响应面法修正后的有限元模型计算的模态频率和“真值模型”十分接近,证实了应用响应面法进行模型修正的可行性。表4给出了“真值模型”的结构参数与修正前后有限元模型的结构参数的对比。很显然:修正前初始模型与“真值模型”结构参数之间的误差较大,而修正后的模型的结构参数与“真值模型”充分接近。 图4是应用两种响应面法对悬臂梁进行修正得到的收敛曲线。从图中可以看出,基于两种响应面法的修正迭代过程都是在第8次迭代时收敛,表明了应用响应面法进行模型修正的高效性,同时两种响应面方法在悬臂梁模型修正过程中优劣不明显。 表3 悬臂梁模型修正前后模态频率结果列表 表4 悬臂梁模型修正前后设计变量结果列表 图4 基于不同响应面法的悬臂梁修正过程中的收敛曲线Fig.4 Convergence curve in the process of cantilever beam updating based on different response surface methods 采用无线磁电式速度传感器对QTZ125型塔机进行了风振响应的现场实测,塔机起重臂、平衡臂以及塔身上各对称布置有两个传感器,分别测量了结构的竖直方向和水平方向速度响应,测点布置如图5所示。通过模态识别技术获得了QTZ125型塔机的动态特性,得到了塔机的低阶固有频率和振型如表5所示。 图5 传感器测点布置Fig.5 The layout of the sensor measurement points 阶次频率/Hz振型10.12起重臂回转平面一阶弯曲20.27起重臂起升平面一阶弯曲30.33塔身回转平面一阶弯曲40.62塔身起升平面一阶弯曲 塔式起重机的有限元模型在ANSYS平台中采用自下而上的建模方式得到,结构中有5 824个Beam189单元、4个Link8单元、26个Mass21单元,共有11 052个节点、66 320个有限元自由度。依据工程实践经验,选取对响应影响较大的塔机结构的主要几何参数和材料参数进行灵敏度分析,得到各阶频率对参数的灵敏度如图6所示,选取7个灵敏度较高的参数作为待修正参数,列于表6中。图中L1~L5分别表示相邻斜腹杆铰接距离、塔身标准节主肢长度、水平腹杆长度、主肢截面宽度及上塔身水平腹杆长度;T1为塔身主肢截面厚度;S11、S12分别为平衡臂尾部凸缘长度和主梁尾部高度;S21、S22、S23分别为起重臂下弦杆壁厚、斜腹杆壁厚以及上弦杆外径;E、μ为杨氏模量与泊松比。 图6 塔机各阶模态频率对结构参数的灵敏度Fig.6 Sensitivity of the tower crane modal frequencies to structural parameters 序号参数参数说明初始值/mm1x1塔身标准节主肢长度13002x2上塔身水平腹杆长度13903x3塔身水平腹杆长度18504x4平衡臂尾部凸缘长度885x5起重臂下弦杆壁厚106x6平衡臂主梁尾部高度3207x7塔身主肢截面宽度150 拟合得到的塔机两种响应面模型的有效性评价如表7所示。可以发现:塔机前四阶频率的两种响应面的决定系数R2的值都接近于1,相对均方根误差RMSE的值都接近于0。因此,用该响应面模型来替代塔机有限元模型进行模型修正是可靠的,也验证了塔机待修正参数选取的合理性。可以发现,结合工程实践经验与参数灵敏度分析获得待修正参数是有效的,同时对结构进行修正时选择结构的几何参数或材料参数作为修正参数都是可行的,本文塔机实例中比较灵敏的结构参数恰好全部为长度或厚度等几何参数。 图7 塔机各阶频率的响应面与有限元模型计算结果对比Fig.7 Comparison of modal frequencies of the tower crane response surface and finite element model calculation 模态阶次二次响应面R2RMSE/10-3高斯响应面R2RMSE/10-310.99840.730.99940.4420.99311.500.99910.5230.99870.730.99880.6940.99821.000.99172.20 将拟合得到的响应面方程应用最优化理论进行优化迭代,得到整个迭代过程的收敛曲线如图8所示。在同一计算系统上计算时,采用传统的模型修正方法对塔机进行修正每迭代一次需耗时1.5 h;而采用高斯响应面和二次响应面进行修正时,整个优化过程的计算时间分别只需要8 s和3 s,可见采用响应面方法可以极大地提高优化效率,同时二次响应面模型的迭代收敛速度更快,且收敛精度更高。图9、图10分别为塔机修正过程中各阶频率和参数的收敛曲线,其中图10中各参数依据初值进行了无量纲化处理。从图中可以看出,基于两种响应面法的修正迭代过程中各阶频率和参数约在第15次迭代时收敛。 利用两种响应面方法获得的塔机修正前后的模态频率和结构参数的结果分别如表8和表9所示。从表8和表9中可以发现:修正后塔机模型的模态频率和结构参数数值较之初始模型更接近真实模型,各阶振型吻合较好,模态置信因子(MAC)均大于90%,验证了利用响应面方法进行塔机有限元模型修正的有效性;同时,与高斯响应面模型修正结果相比,二次响应面模型的修正精度更高。 图8 基于不同响应面法的塔机 图9 塔机各阶频率修正过程中 图10 塔机各修正参数修正过程中 修正过程中的收敛曲线 的收敛曲线 的收敛曲线Fig.8 Convergence curve in the process of tower crane Fig.9 Convergence curve of frequencies Fig.10 Convergence curve of parameters updating based on different response surface methods in tower crane updating in tower crane updating 模态阶次真实模型/Hz初始模型频率/Hz误差/%二次响应面修正后模型频率/Hz误差/%高斯响应面修正后模型频率/Hz误差/%MAC/%10.120.1416.70.1200.00.1221.795.620.270.3218.50.2731.10.260-3.793.630.330.3918.20.326-1.20.320-3.091.040.620.7216.10.6210.20.610-1.694.8 表9 塔机模型修正前后结构参数结果列表 本文提出了塔式起重机有限元模型修正的响应面方法。首先联合运用经验选择方法和灵敏度分析方法来选取待修正参数,接着选用均匀设计方法设计试验,拟合模态频率与结构参数之间二次响应面模型和高斯响应面模型。然后采用F检验法对响应面的各参数进行显著性分析,建立更简单有效的响应面模型,用得到的响应面模型代替原有的有限元模型完成模型修正。本文的研究表明: (1)利用响应面模型替代复杂的塔机有限元模型进行结构有限元模型修正可以极大地提高计算效率和修正精度。 (2)对于塔机结构,相较于基于高斯径向基函数的响应面法,基于二次多项式响应面的模型修正能取得更好的修正结果和修正效率。 [ 1 ] 秦仙蓉,徐俭,赵坤,等. 基于分层进化寻优的塔机结构有限元模型修正[J]. 同济大学学报(自然科学版), 2015, 43(6): 900-903. QIN Xianrong, XU Jian, ZHAO Kun, et al. Dynamic model hierarchy updating of tower crane using evolutionary computation[J]. Journal of Tongji University (Natrral Science), 2015, 43(6): 900-903. [ 2 ] 杜青,蔡美峰,张献民,等. 钢筋混凝土桥梁结构动力有限元模型修正[J]. 公路交通科技, 2006, 23(1): 60-62. DU Qing, CAI Meifeng, ZHANG Xianmin, et al. RC bridges dynamic finite element model updating[J]. Journal of Highway and Transportation Research and Development, 2006, 23(1):60-62. [ 3 ] 徐向宏,何明珠. 试验设计与Design-Expert、SPSS应用[M]. 北京: 科学出版社, 2010. [ 4 ] 任伟新, 陈华斌. 基于响应面的桥梁有限元模型修正[J]. 土木工程学报, 2008, 41(12):73-78. REN Weixin, HE Huabin. Response-surface based on finite element model updating of bridge structures[J]. China Civil Engineering Journal, 2008, 41(12):73-78. [ 5 ] 邓苗毅, 任伟新, 王复明. 基于静力响应面的结构有限元模型修正方法[J]. 实验力学, 2008, 23(2):103-109. DENG Miaoyi, REN Weixin, WANG Fuming. Structure finite element model (FEM) updating based on static-load response surface methodology[J]. Experimental Mechanics, 2008, 23(2):103-109. [ 6 ] 宗周红, 高铭霖, 夏樟华. 基于健康监测的连续刚构桥有限元模型确认(Ⅰ)——基于响应面法的有限元模型修正[J]. 土木工程学报, 2011(2):90-98. ZONG Zhouhong, GAO Minglin, XIA Zhanghua. Finite element model validation of the continuous rigid frame bridge based on structural health monitoring PartⅠ:FE model updating based on the response surface method[J]. China Civil Engineering Journal, 2011(2):90-98. [ 7 ] SHAN D, LI Q, KHAN I, et al. A novel finite element model updating method based on substructure and response surface model[J]. Engineering Structures, 2015, 103:147-156. [ 8 ] ZHOU L, WANG L, CHEN L, et al. Structural finite element model updating by using response surfaces and radial basis functions[J]. Advances in Structural Engineering, 2016, 19(9):1446-1462. [ 9 ] 郭勤涛,张令弥,费庆国. 用于确定性计算仿真的响应面法及其试验设计研究[J]. 航空学报, 2005, 127(11): 55-61. GUO Qintao, ZHANG Lingmi, FEI Qingguo. Response surface method and its experimental design for deterministic computer simulation[J]. Acta Aeronautica et Astronautica Sinica, 2005, 127(11): 55-61. [10] 马成良,张海军,李素萍. 现代试验设计优化方法及应用[M]. 郑州: 郑州大学出版社, 2007. [11] 方开泰. 均匀设计与均匀设计表[M]. 北京: 科学出版社, 1994. [12] 宗周红,任伟新. 桥梁有限元模型修正和模型确认[M]. 北京: 人民交通出版社, 2012. [13] 万华平,任伟新,魏锦辉. 基于高斯过程响应面的结构有限元模型修正方法[J]. 振动与冲击, 2012 , 31(24): 82-87. WAN Huaping, REN Weixin, WEI Jinhui. Structural finite element model updating based on Gaussian process response surface methodology[J]. Journal of Vibration and Shock, 2012 , 31(24): 82-87. [14] DENG L, ASCE A M, CAI C S, et al. Bridge model updating using response surface method and genetic algorithm[J]. Journal of Bridge Engineering, 2010, 15(5):553-564. [15] SHAHIDI S G, PAKZAD S N. Generalized response surface model updating using time domain data[J]. Journal of Structural Engineering, 2014, 140(140):A4014001.1.4 响应面有效性评价
1.5 优化问题的数学建模
2 悬臂梁算例分析

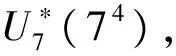
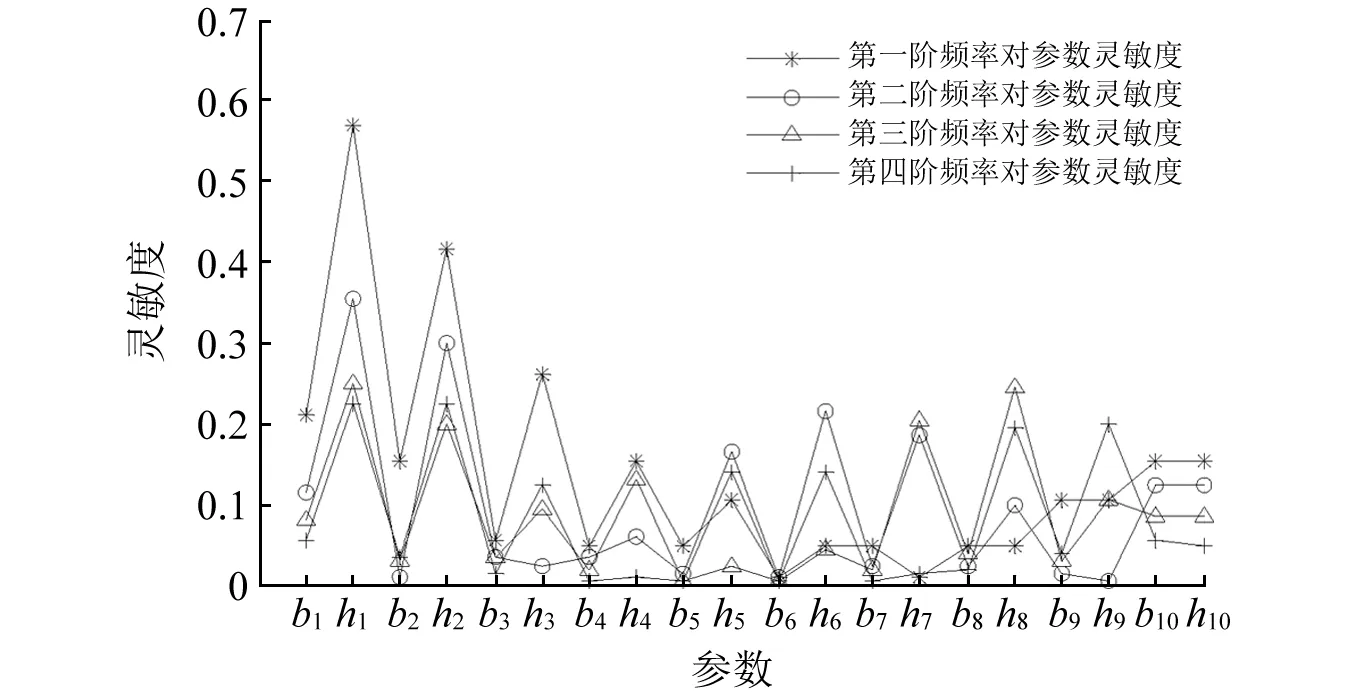
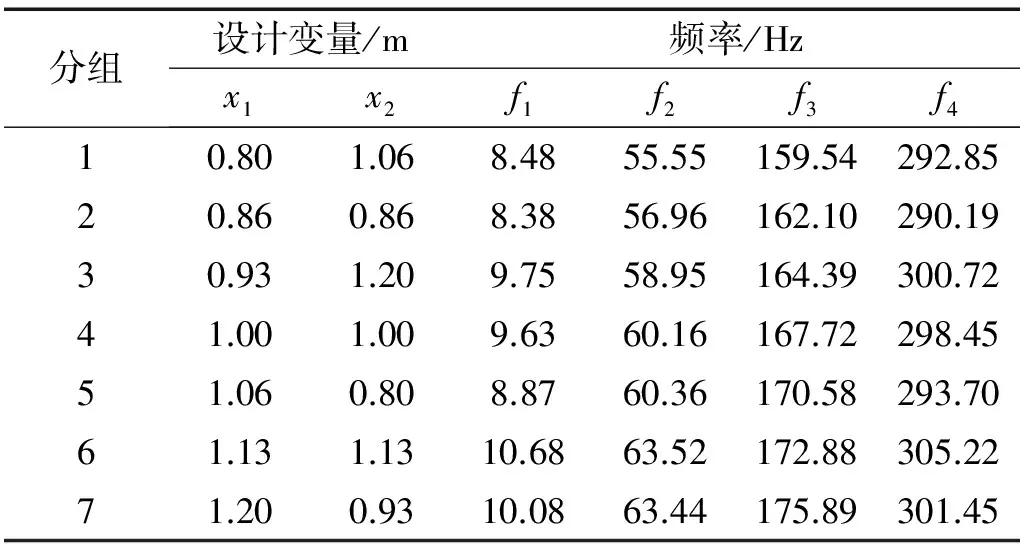
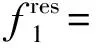
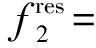
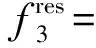
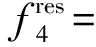
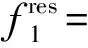
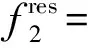
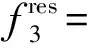
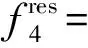
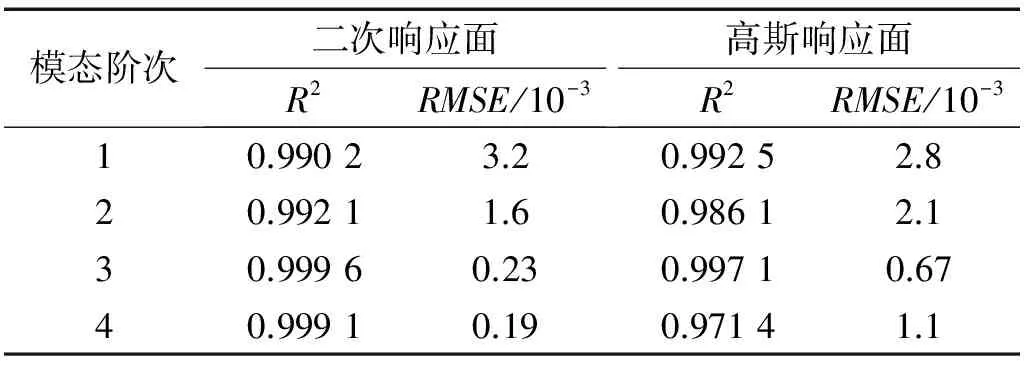
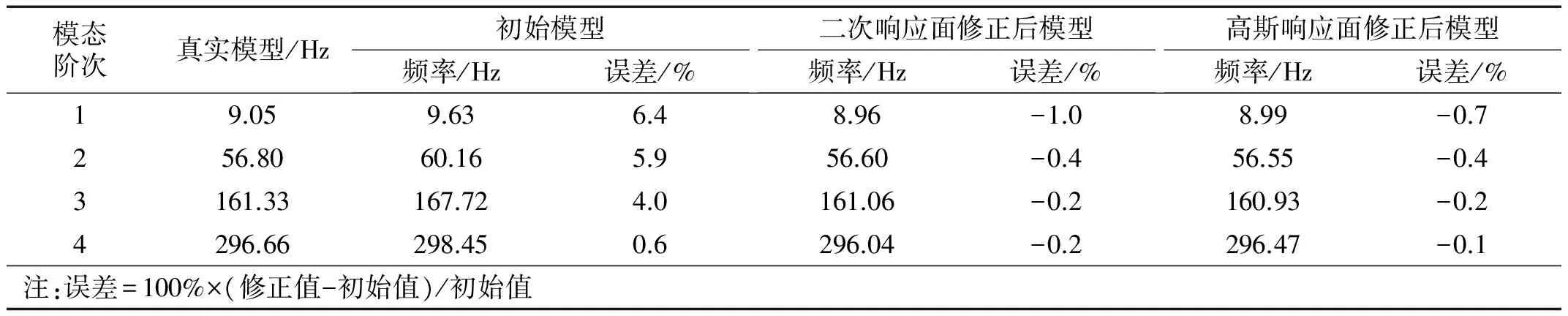

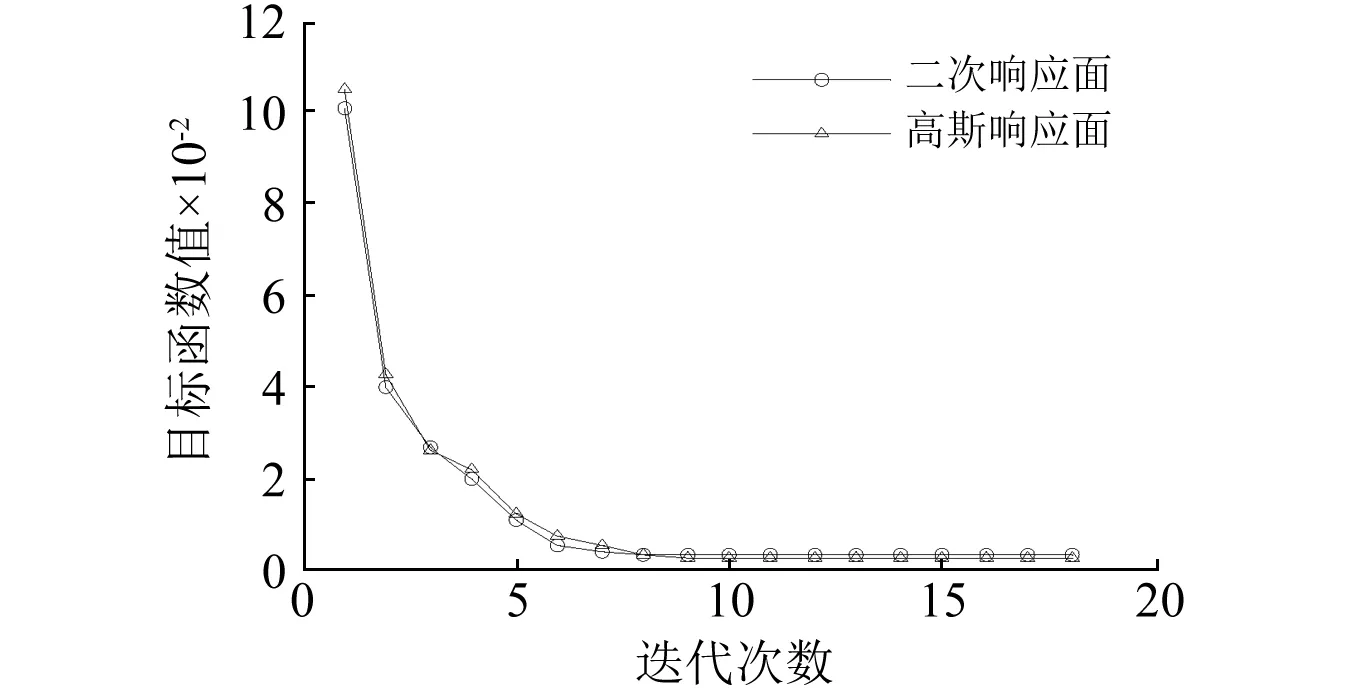
3 工程实例


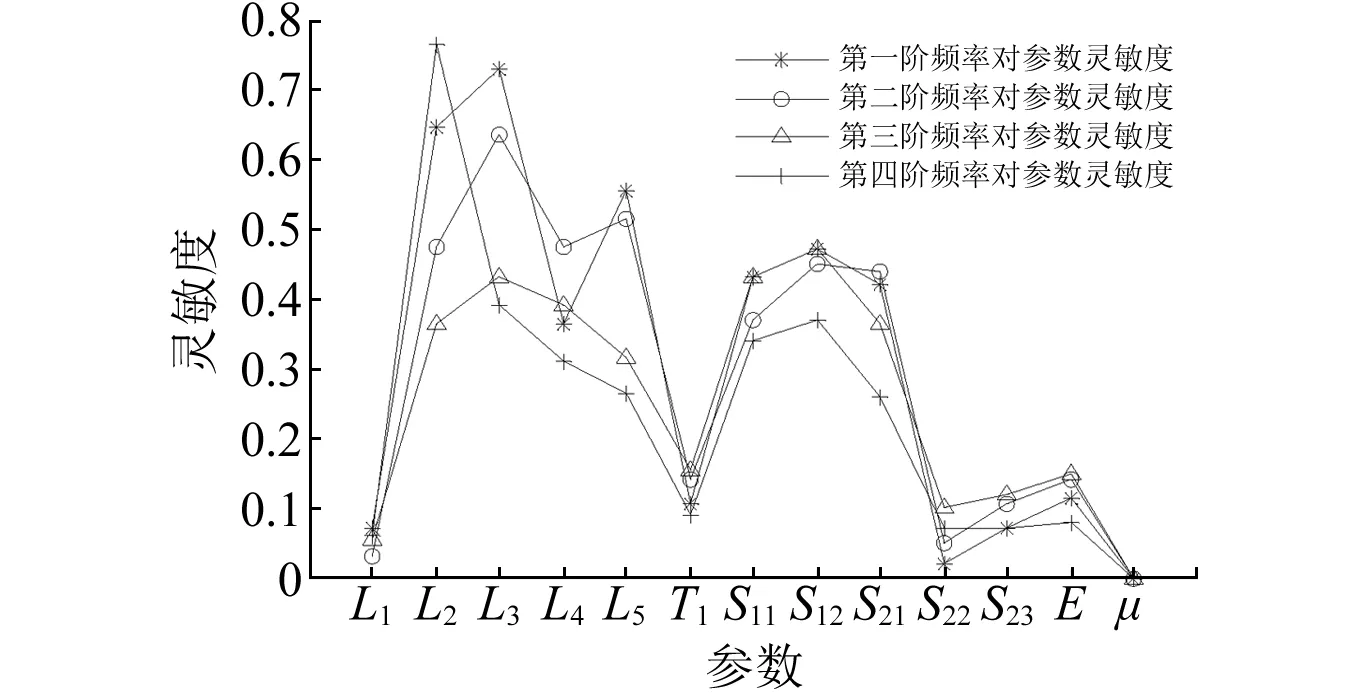

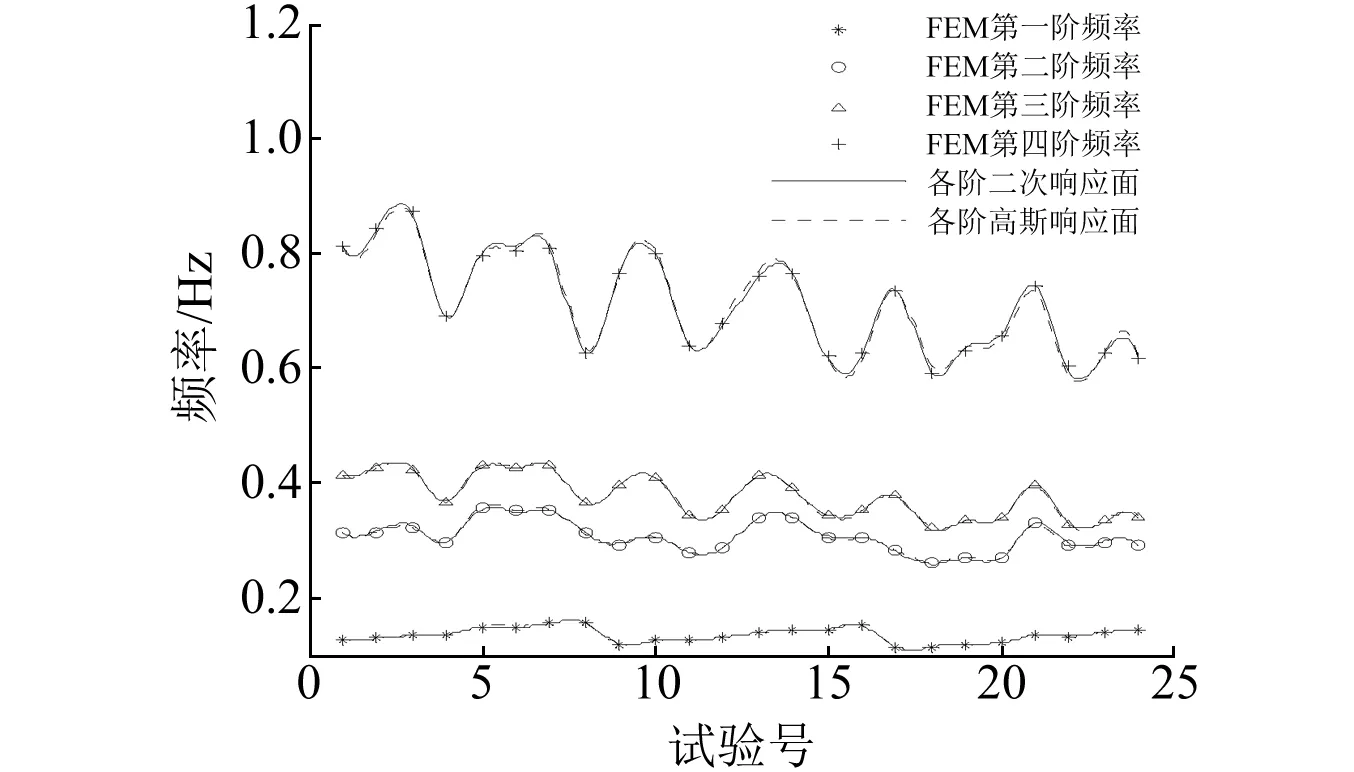


4 结 论
