基于MOMEDA与Teager能量算子的滚动轴承故障诊断

祝小彦， 王永杰

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

旋转机械设备中滚动轴承是重要的组成零部件之一，由于轴承故障造成机毁人亡的事故时有发生，因此对滚动轴承的状态检测和故障诊断有着重要意义。但因工况的复杂性所测振动信号具有非平稳性，且早期故障轴承振动信号中反应故障特征的冲击成分较微弱，极易被噪声覆盖，较难直接由时域或频域判断故障类型[1]。因此，滚动轴承的早期故障诊断一直以来都是研究的难点和热点。

滚动轴承故障源信号的传递过程可以看作是源信号与信道的一个线性卷积混合过程，提取故障原始冲击信号则可以看作是一个解卷积的过程。从这个角度出发，Wiggins[2]提出了最小熵解卷积(Minimum Entropy Deconvolution, MED)并成功应用到了地震波的处理中。近年来，不少研究人员将MED解卷积算法引入到滚动轴承故障诊断中。柳玉昕等[3]通过将最小熵与Teager能量算子相结合并在包络谱中找到了多个倍频，但干扰频率幅值较大，解卷积效果欠佳。冷军发等[4]将MED应用于滚动轴承早期故障诊断只得到了基频与2倍频，且包络谱中噪声影响严重。王宏超等[5]提出了基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取方法成功提取到了3倍频，但从包络谱中可以看出噪声的影响仍然较大。研究发现最小熵解卷积算法在处理滚动轴承故障信号时并不完全适用，主要包括以下三点：①MED定义故障信号第一个采样点之前的幅值为零，造成了MED解卷积信号中伪冲击成分的出现；②MED算法采用迭代的方式只能找到局部最优滤波器，并不一定是全局最优滤波器；③对于多点连续性冲击的滚动轴承故障信号，MED解卷积信号中往往只有一个或者几个冲击成分，显然这样的解卷积结果并不能反映轴承故障时的真实情况。

针对以上问题，Mcdonald等[6]提出了一种新的解卷积方法——多点最优调整的最小熵解卷积(Multipoint Optimal Minimum Entropy Deconvolution Adjusted，MOMEDA)。MOMEDA针对旋转机械故障信号的特点对解卷积的定义作了改进，并引入了目标向量和多点D-范数，不仅解决了最优滤波器的设计问题，而且实现了对轴承故障信号中的连续多点冲击成分准确提取。

本文首次将多点最优调整的最小熵解卷积算法应用到滚动轴承早期故障诊断中，提出了基于MOMEDA和Teager能量算子的滚动轴承早期故障诊断方法。仿真和实测信号的分析表明该方法在滚动轴承早期故障的诊断中具有一定的有效性和实用性。

1 MOMEDA算法

假设y为故障轴承的一个冲击信号，h为系统频响函数，x为传感器采集到的振动信号，e为随机噪声。则冲击信号由信源到传感器的传输过程可以近似地表达为

x=h*y+e

(1)

MOMEDA算法的核心部分是要通过非迭代的方式找到一个最优滤波器f，实现对原冲击信号y的重构，并尽量削减噪声对提取冲击信号的影响。解卷积过程为

(2)

式中：k=1,2,…,N-L。MOMEDA算法针对旋转机械故障信号中存在周期性冲击的特点，在D-范数的基础上提出了多点D-范数。即

多点D-范数

(3)

(4)

式中：t为目标向量，定义了解卷积目标冲击成分的位置和权重。当目标向量t与原冲击信号y完全契合时，解卷积效果达到最佳。此时多点D-范数取到最大值，与之对应的滤波器就是一组最优滤波器f。

式(4)的求解问题等价于求解方程

(5)

式中：f=f1,f2,f3,…,fL，t=t1,t2,t3,…,tN-L。

由式(2)、式(4)、式(5)可以求得

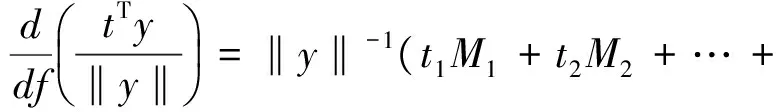
(6)

式中：k=1,2,…,N-L。

令X0=[M1，M2， …，Mk]，则式(6)简记为

‖y‖-1X0t-‖y‖-3tTyX0y=0

(7)

整理得

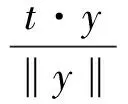
(8)

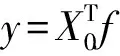
(9)

取其特解作为一组最优滤波器，记为

(10)

2 Teager 能量算子

Teager能量算子是一种非线性差分算子，相对于传统的信号能量定义，它增加了和频率平方根的乘积，更能够突出冲击的瞬时特征[7]。

对于调幅调频信号x(t)=a(t)cos[Φ(t)]，Teager能量算子Ψ的定义为

(11)

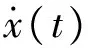
式(11)展开整理得

Ψ[x(t)]=[a(t)φ′(t)]2+a2(t)φ″(t)×
sin[2φ(t)]/2+cos2[φ(t)]Ψ[a(t)]

(12)

由于通常调制信号比载波信号变化慢得多，所以其幅频值可近似视为常数处理[8]。令Ψ[a(t)]=0,φ″(t)=0，可得

Ψ[x′(t)]≈[a(t)φ′(t)]2=a2(t)ω2(t)

(13)

同理可得

Ψ[x′(t)]≈a2(t)ω4(t)

(14)

由式(13)和式(14)分别计算x(t)的瞬时幅值和瞬时相位

(15)

(16)

Teager能量算子对信号能量的定义中包含了信号的动能和势能。与传统能量的定义方式相比，Teager能量算子能够较大程度上增强信号的幅值。然而研究发现，在实际应用中Teager能量算子对冲击信号与噪声信号并没有太大的分辨能力，算法在增强冲击信号幅值的同时，信号中噪声的幅值也会相应的增加，使得在包络谱中难以出现故障特征频率。因此有必要对原始故障信号进行滤波处理，提高信噪比。

3 故障诊断流程

滚动轴承早期故障信号中，冲击成分往往比较微弱，在强背景噪声的影响下故障检测更加困难。MOMEDA算法不仅能够找到最优滤波器而且能够准确提取出故障信号中周期性的冲击信号，尤其适合于处理滚动轴承早期故障信号。然而笔者研究发现，直接对MOMEDA解卷积信号包络分析其故障特征频率并不十分突出，为此本文进一步提出利用Teager能量算子增强故障信号，从而使故障特征频率在包络谱中更加明显。本文中尝试将MOMEDA算法应用到滚动轴承故障诊断领域，并针对轴承早期故障信号的特点，提出了MOMEDA算法与Teager能量算子相结合的诊断方法。具体实现步骤：①利用MOMEDA算法提取滚动轴承早期故障信号中连续性周期冲击成分；②借助于Teager能量算子对解卷积输出信号中的冲击成分进一步突出；③通过比较包络谱中主导频率成分与滚动轴承各元件故障特征频率判断故障轴承的故障类型。主要流程如图1所示。

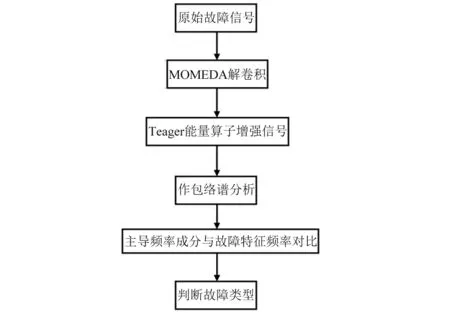
图1 故障诊断流程图Fig.1 The flowchart of fault diagnosis

4 仿真实验

利用滚动轴承故障模型[9-11]对内圈故障时产生的冲击信号进行模拟，并添加强烈白噪声模拟轴承内圈早期故障信号。仿真信号为

(17)

式中：s(t)为周期性冲击成分；n(t)为高斯白噪声； 幅值为A0为0.5；τi为第i次冲击相对于周期T的微小波动； 衰减系数C为800； 共振频率fn为4 000 Hz； 转频fr为20 Hz，内圈故障特征频率fi=1/T=110 Hz，随机波动服从零均值正态分布，标准差为转频的0.5%，仿真信号信噪比为-13 dB，采样频率fs为12 000 Hz，采样点数N为8 192。仿真信号时域图、幅值谱、Teager能量算子包络谱如图2所示。

从图2(a)中可以看出，由于在冲击信号中添加了较重的噪声信号，冲击成分已经完全淹没在噪声信号中，时域波形中难以找到明显的周期性冲击特征。图2(b)仿真信号频谱中由于冲击信号特征频率及其倍频与转频及其倍频之间调制现象的发生，以及信号中强烈的噪声信号的干扰，虽然能够在频谱中找到较突出的频率成分但发现都是干扰频率，并不能反映滚动轴承内圈的故障信息。图2(c)是仿真信号直接经过Teager能量算子解调之后得到的Teager能量算子包络谱，可以看出由于信号中强烈噪声的影响包络谱中仍然难以找到明显的故障特征频率成分。通过以上分析可知：轴承早期故障信号中微弱的冲击信号常常会被背景噪声所淹没，单纯地利用Teager能量算子包络谱难以实现对滚动轴承内圈的准确识别，因此有必要在Teager能量算子包络分析之前对故障信号进行滤波处理，提高信噪比。

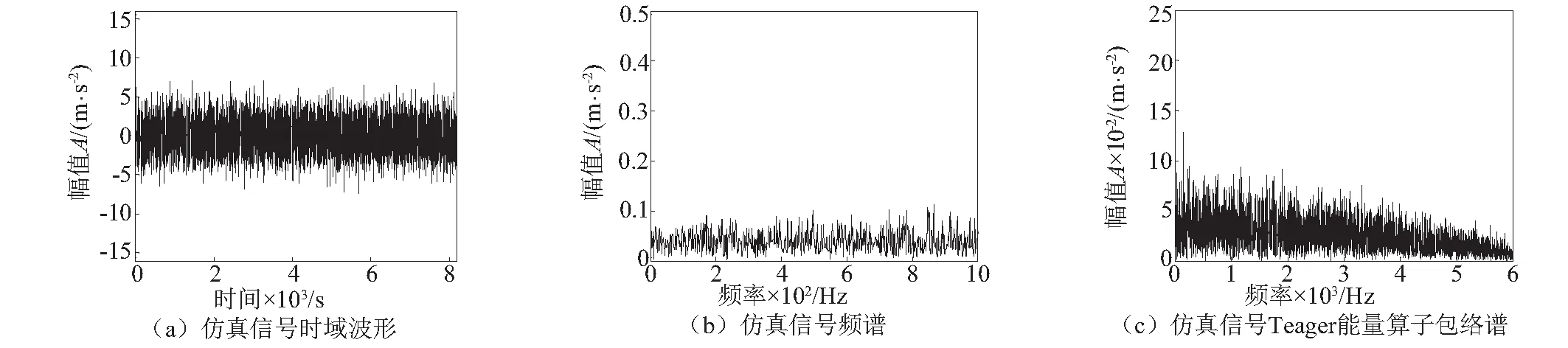
图2 仿真信号时域波形、频谱及其Teager能量算子包络谱Fig.2 Time domain waveform, spectrum and Teager energy operator envelope spectrum of simulation signal

图3(a)是MOMEDA对仿真信号解卷积(滤波器阶数为1 000，窗函数[1 000,1]，周期为109)后的时域波形，可以明显看到有周期性的冲击成分存在。图3(b)中利用Teager能量算子对MOMEDA解卷积信号中的冲击成分进一步增强并作包络分析，可以清晰的看到轴承内圈故障特征频率及其倍频fi～9fi。

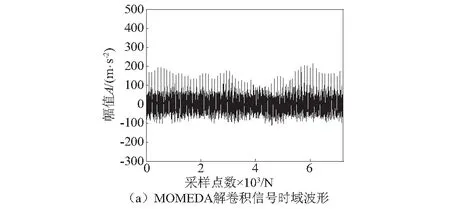
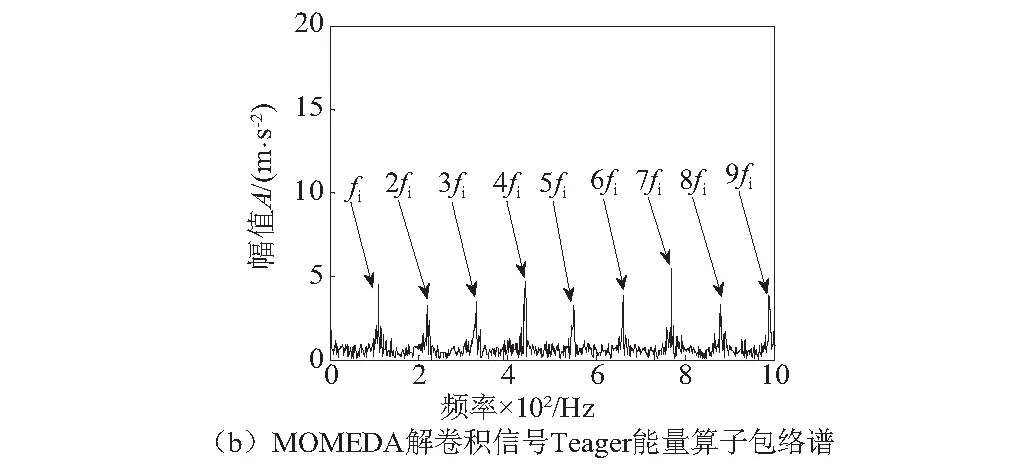
图3 MOMEDA解卷积信号时域波形及其Teager能量算子包络谱Fig.3 Time domain waveform and Teager energy operator envelope spectrum of MOMEDA demodulation

滚动轴承内圈早期故障信号模拟实验表明：轴承故障发生早期故障信号中的冲击成分被强烈的噪声信号所淹没，仅仅利用时域波形、幅值谱难以发现故障相关的频率特征。而Teage能量算子在增强故障信号中的冲击信号的同时噪声信号也随之增强，因此在Teage能量算子包络谱中仍然难以发现明显的故障特征频率。通过故障仿真发现，MOMEDA算法能够对故障信号中冲击成分进行有效提取，通过Teager能量算子对故障信号中冲击成分的进一步增强作包络分析后可以清楚地看到轴承内圈故障特征频率及其多个倍频成分，证明了本文所提方法在提取故障信号中冲击特征的有效性。

5 实测故障信号分析

5.1 人工植入轴承故障

实验数据采用美国凯斯西储大学电气工程实验室滚动轴承滚动体故障信号。实验中所用驱动端滚动轴承型号为SKF 6205，具体参数如下表所示。采用电火花技术在轴承上加工单点凹痕模拟故障早期故障，人为加工的轴承损伤直径分为0.177 8 mm、0.355 6 mm和0.533 4 mm，为体现本文所提方法的有效性，选用故障程度最轻的0.177 8 mm。传感器采样频率为12 kHz，电动机转速为1 797 r/min。滚动体扰动频率为4.713 5 Hz，计算可知滚动体故障特征频率fb为141.2 Hz。电动机转频fr为29.95 Hz。

表1 SKF 6205轴承结构参数

驱动端滚动轴承故障时域波形如图4所示，由于原始故障信号中的冲击成分被强噪声淹没，因此在时域波形中难以观察到明显而有规律性的冲击特征。图5原始信号频谱图中虽然能够找到多条明显谱线，但都不能反映滚动轴承的故障特征。对原始故障信号作Teage能量算子包络分析，结果如图6所示，包络图中只能观察到电动机转频fr及2fr，并没有滚动轴承故障特征频率及其倍频出现，所以难以判断轴承故障类型。

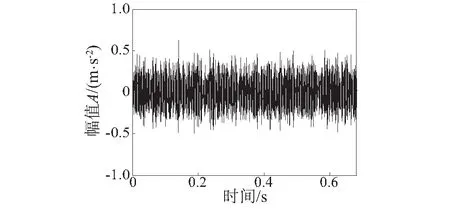
图4 原始故障信号时域波形Fig.4 Time domain waveform of fault signal

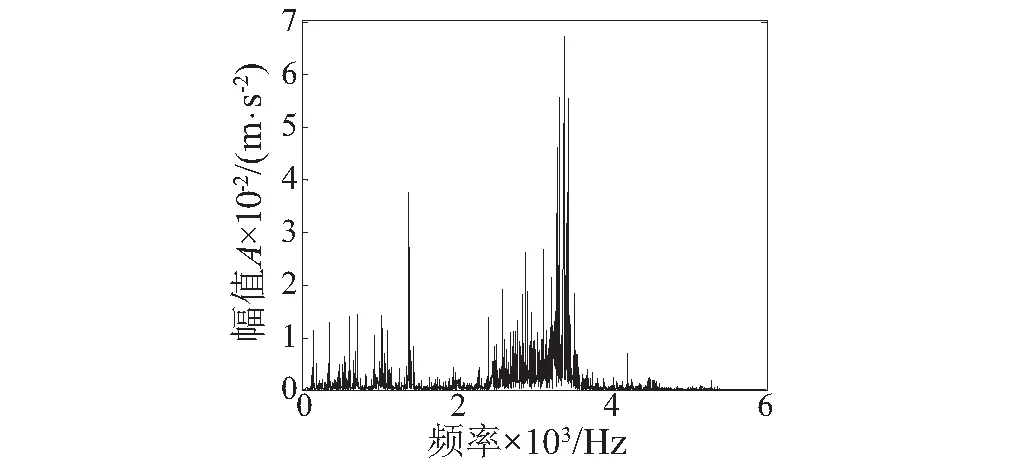
图5 原始信号频谱图Fig.5 Spectrum of original fault signal

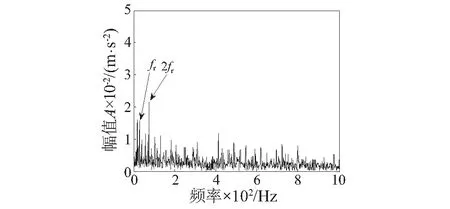
图6 原始故障信号Teager能量算子包络谱Fig.6 Teager energy operator Envelope spectrum of original fault signal

如图7所示，MOMEDA解卷积信号(滤波器阶数为1 500，窗函数[1 500,1]，周期为85.1)时域波形及其包络谱。在图7(a)MOMEDA解卷积信号中可以明显看到信号中的周期性冲击成分。图7(b)中对MOMEDA解卷积信号直接作包络，结果显示，包络谱中可以找到多个相关的滚动体故障特征频率谱线，但并不十分突出。

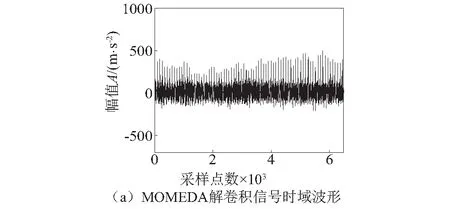
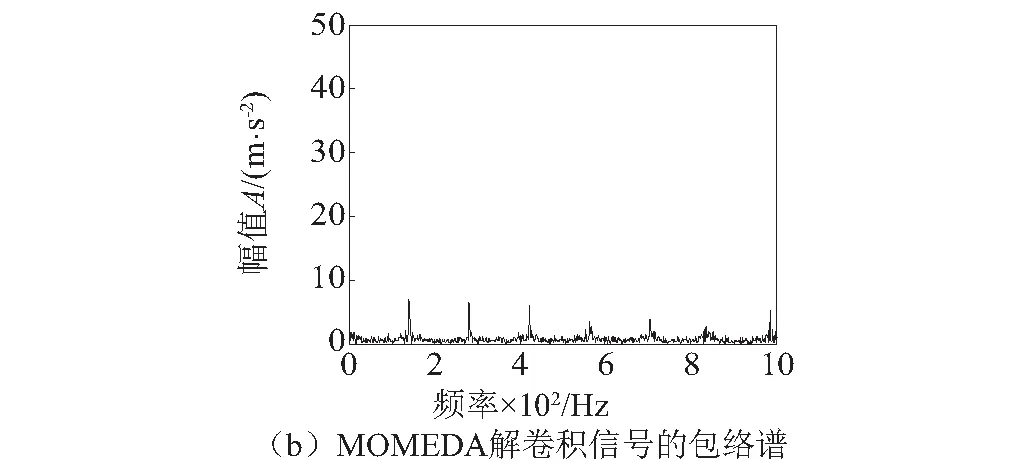
图7 MOMEDA解卷积信号时域波形及其包络谱Fig.7 Time domain waveform and envelope spectrum of MOMEDA demodulation

图8中利用Teager能量算子对MOMEDA解卷积信号中的冲击成分作进一步增强，然后对增强解卷积信号作包络分析，可以看到包络谱中故障特征频率更加明显、突出，与图7(b)相比故障特征频率更明显。由包络谱中故障特征频率可以断定滚动轴承的滚动体发生了故障，分析结果与实际情况一致，证明了本文所提方法的有效性。

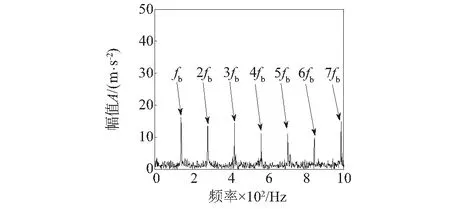
图8 MOMEDA解卷积信号Teager能量算子包络谱Fig.8 Teager energy operator envelope spectrum of MOMEDA demodulation

为了证明本文所提方法的优越性，利用MED算法(滤波器阶数为1 500，迭代次数为100，迭代终止条件为0.001)提取原始故障信号中的冲击成分，并利用Teager能量算子包络谱对MED解卷积信号中的滚动体故障特征频率进行包络分析，结果如图9所示。

如图9(a)所示，MED解卷积信号中只有少量冲击成分出现，解卷积效果并不理想，难以准确提取出旋转机械故障信号中包含的连续性周期冲击成分。图9(b)中，Teager能量算子包络谱中无法看到与滚动体故障相关的频率成分。对比发现，本文所提方法在提取故障信号连续性周期冲击特征方面有着明显的优势。

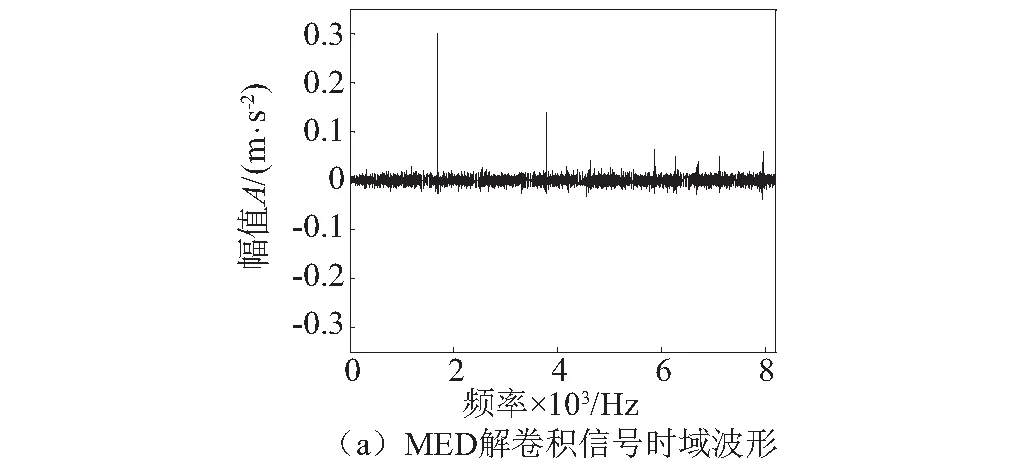
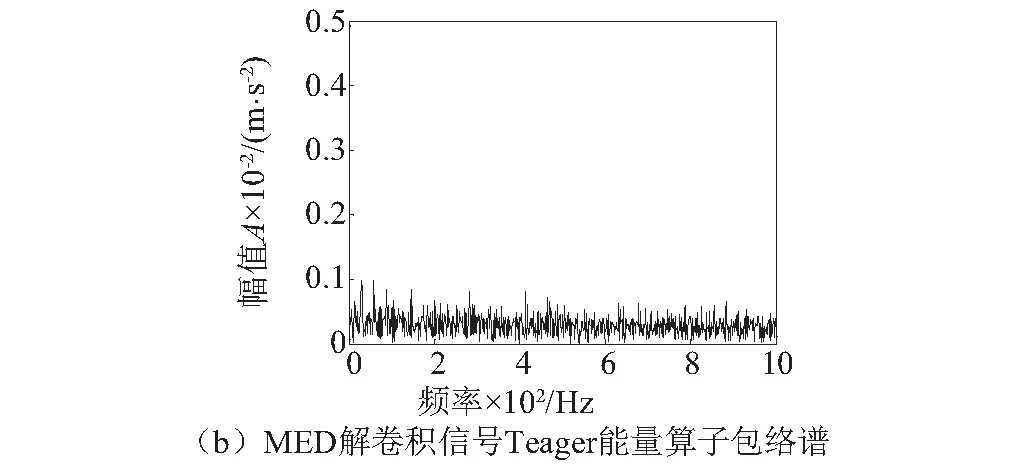
图9 MED解卷积信号时域波形及其Teager能量算子包络谱Fig.9 Time domain waveform and Teager energy operator envelope spectrum of MED demodulation

5.2 全寿命周期加速试验信号

试验分析数据来自NSFI/UCR智能维护系统中心的滚动轴承全寿命周期加速度试验[12-14]，试验台布局如图10所示。试验台转轴上安装有4个型号为ZA2115滚动轴承，其结构参数如表2所示。并利用弹性系统在轴承和转轴上加载约2 671 N的径向载荷，转轴转速为2 000 r/min。滚动轴承轴向和径向分别安装有353B33型高灵敏度ICP加速度传感器。试验过程中共进行3组试验，利用NI DAQCard-6062采集卡采集试验振动信号，采样频率为20 kHz。其中第二组试验持续时间为164 h，共采集数据文件984个，采样间隔为10 min，采样点数为20 480。本文中数据选用第二组试验数据对一号滚动轴承外圈故障进行分析。经计算，轴承外圈故障特征频率fo为236.4 Hz。

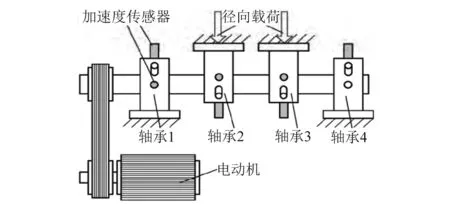
图10 试验台示意图Fig.10 Schematic diagram of experiment platform

轴承型号轴承节径滚动体直径滚动体数接触角ZA211571．5mm8．4mm1615．17°

如图11所示，试验轴承在0～9 790 min全寿命周期内，表征轴承故障程度的均方根值发生了显著的变化。约5 100 min之后轴承故障开始有所增加，但波动幅度并不大，这一阶段一般称之为轴承故障的早期阶段；而在7 020 min轴承振动信号的均方根值发生了突变，轴承故障进一步加剧，直到试验最后均方根值达到最大轴承失效。试验结束后在轴承外圈上发现了明显的剥蚀现象。

为了验证本方法对滚动轴承早期故障的有效性，本文选择5 310 min时故障刚开始发生时的试验数据

进行分析。图12为早期故障信号的时域波形、频谱图及其Teager能量算子包络谱。原始信号频谱图中虽然出现了许多较突出的频率成分，但观察发现这些频率成分都是干扰频率，并不能正确反映轴承故障。而在Teager能量算子包络谱中也没有出现较突出的外圈故障特征频率。

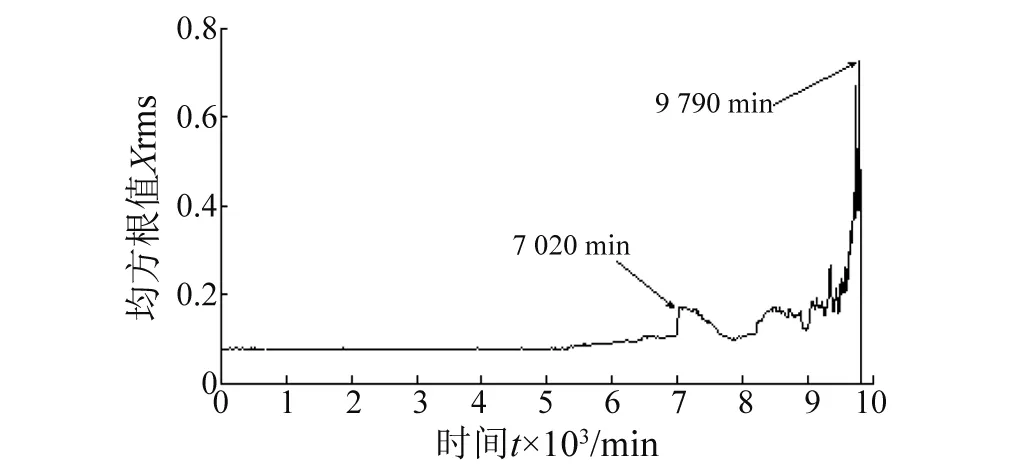
图11 轴承故障发展趋势图Fig.11 Bearing fault tendency chart

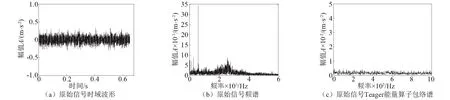
图12 原始信号的时域波形、频谱图及其Teager能量算子包络谱Fig.12 Time domain waveform, spectrum and Teager energy operator envelope spectrum of original signal

图13为MED算法的解卷积信号(滤波器阶数为1 500，迭代次数为100，迭代终止条件为0.001)及其Teager能量算子包络谱，可以看出MED解卷积信号中并没有出现连续性冲击信号，在其Teager能量算子包络谱中也没有发现与轴承外圈故障特征频率相关的谱线出现。

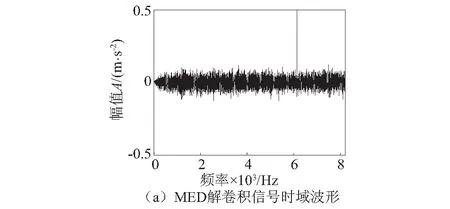
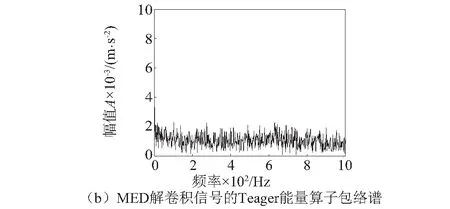
图13 MED解卷积信号时域波形及其Teager能量算子包络谱Fig.13 Time domain waveform and Teager energy operator envelope spectrum of MED demodulation

采用本文所提方法对轴承早期故障信号进行分析，图14为MOMEDA解卷积信号及其包络谱。与MED解卷积信号相比，图14(a)MOMEDA解卷积信号(滤波器阶数为1 500，窗函数[1 500,1]，周期为50.8)中出现了连续性周期冲击成分。直接对MOMEDA解卷积信号进行包络分析，结果如图14(b)所示。

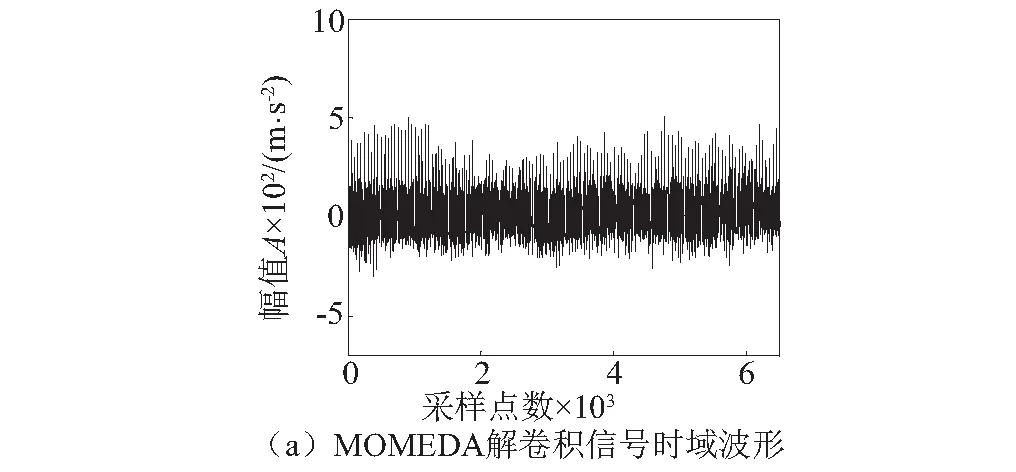
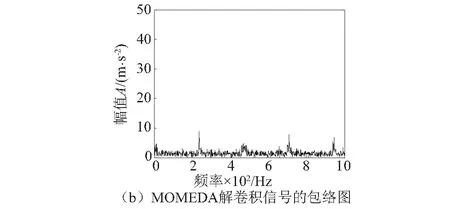
图14 MOMEDA解卷积信号时域波形及其包络谱Fig.14 Time domain waveform and envelope spectrum of MOMEDA demodulation

包络谱中可以看到轴承外圈故障特征频率及其倍频fo～4fo，但故障频率谱线并不十分突出。图15中对MOMEDA解卷积信号作Teager能量算子包络谱，可以看到包络谱中出现了更加突出的外圈故障特征频率及其倍频，增强效果明显。对比图中主导频率成分与轴承外圈故障特征频率表明轴承外圈已经发生了故障，与试验结果故障类型吻合。

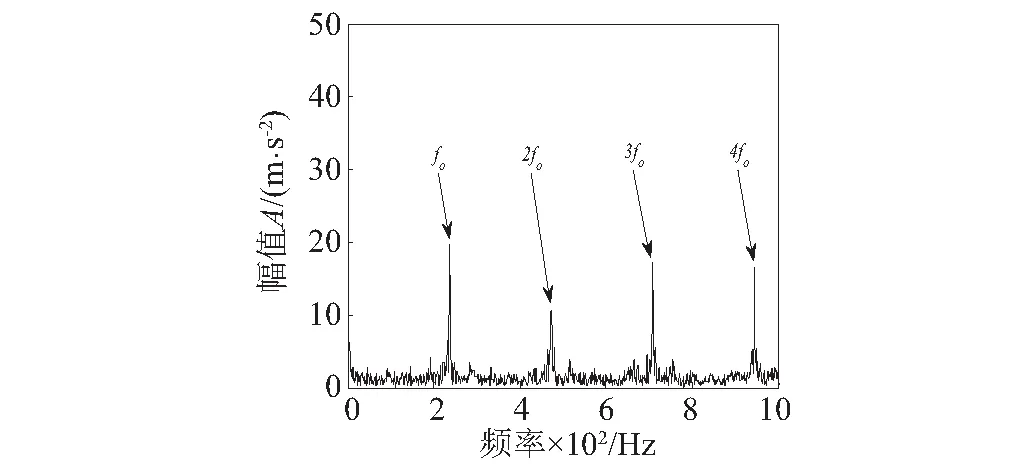
图15 MOMEDA解卷积信号的Teager能量信号包络谱Fig.15 Teager energy operator envelope spectrum of MOMEDA demodulation

6 结 论

(1) 滚动轴承早期故障信号中信噪比较低，原始故障信号中难以找到规律的周期性冲击成分，试验证明MOMEDA算法确实能够有效地提取出故障信号中的冲击信号。与MED算法的解卷积效果相比，MOMEDA算法能够更准确的提取出故障信号中连续性周期冲击成分。

(2)试验结果表明直接对MOMEDA解卷积信号作包络时，包络谱中也能够出现故障特征频率及其倍频，但主导频率成分并不突出。相比之下Teager能量算子包络谱中故障特征频率及其倍频谱线则更加清晰明显，试验证明Teager能量算子能够在一定程度上增强故障信号中的冲击特征。

(3) 通过将MOMEDA算法与Teager能量算子相结合，能够实现对故障信号中的故障特征的有效提取和分析，与单一方法的分析结果相比效果明显，证明了本文所提方法的有效性。

[ 1 ] 余发军,周凤星,严保康.基于字典学习的轴承早期故障稀疏特征提取[J].振动与冲击,2016, 35(6): 181-186.

YU Fajun, ZHOU Fengxing, YAN Baokang. Bearing initial fault feature extraction via sparse representation based on dictionary learning [J].Journal of Vibration and Shock, 2016, 35(6): 181-186.

[ 2 ] WIGGINS R A. Minimum entropy deconvolution[J]. Geoexploration, 1978, 9(16): 21- 35.

[ 3 ] 柳玉昕,石岩,王美俊,等. 基于最小熵解卷积和能量算子的滚动轴承故障诊断方法[J].组合机床与自动化加工技术, 2016(6): 114-117.

LIU Yuxin, SHI Yan, WANG Meijun, et al. A method of fault diagnosis for rolling bearing based on minimum entropy deconvolution and energy operator[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016(6): 114-117.

[ 4 ] 冷军发,杨鑫,荆双喜. 最小熵解卷积在滚动轴承早期故障诊断中的应用[J].机械传动, 2015, 39(8): 189-192.

LENG Junfa, YANG Xin, JING Shuangxi. Application of minimum entropy deconvolution in the rolling element bearing fault diagnosis[J]. Journal of Mechanical Transmission, 2015, 39(8): 189-192.

[ 5 ] 王宏超, 陈进,董广明. 基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J].机械工程学报, 2013, 49(1): 88-94.

WANG Hongchao, CHEN Jin, DONG Guangming. Fault diagnosis method for rolling bearing’s weak fault based on minimum entropy deconvolution and sparse decomposition[J]. Journal of Mechanical Engineering, 2013, 49(1): 88-94.

[ 6 ] MCDONALD G L. ZHAO Q. Multipoint optimal minimum entropy deconvolution and convolution fix: application to vibration fault detection [J]. Mechanical Systems and Signal Processing, 2017, 82: 461-477.

[ 7 ] 王天金,冯志鹏,郝如江,等.基于Teager能量算子的滚动轴承故障诊断研究[J].振动与冲击,2012, 31(2): 1-5.

WANG Tainjin, FENG Zhipeng, HAO Rujiang, et al. Fault diagnosis of rolling element bearings based on Teager energy operator[J]. Journal of Vibration and Shock, 2012, 31(2): 1-5.

[ 8 ] 鞠萍华,秦树人,赵玲,等. 基于LMD的能量算子解调方法及其在故障特征信号提取中的应用[J]. 振动与冲击, 2011, 30(2): 1-4.

JU Pinghua, QIN Shuren, ZHAO Ling, et al. Energy operator demodulating approach based on LMD and its application in extracting characteristics of a fault signal [J]. Journal of Vibration and Shock, 2011, 30(2): 1-4.

[ 9 ] ANTONI J, BNNARDOT F, RAAD A, et al. Cyclostationary modeling of rotating machine vibration signals [J]. Mechanical Systems and Signal Processing, 2004, 18(6): 1285-1314.

[10] 唐贵基,王晓龙.自适应最大相关峭度解卷积方法及其在轴承早期故障诊断中的应用[J].中国电机工程学报, 2015, 35(6): 1436-1444.

TANG Guiji, WANG Xiaolong. Adaptive maximum correlated kurtosis deconvolution method and its application on incipient fault diagnosis of bearing[J]. Proceedings of The Chinese Society for Electrical Engineering, 2015, 35(6): 1436-1444.

[11] RANDALL R B, ANTONI J, CHOBSAARD S. The relationship between spectral correlation and envelope analysis in the diagnosis of bearing faults and other cyclostationary machine signals [J]. Mechanical Systems and Signal Processing, 2001, 15(5): 945-962.

[12] 马伦,康建设,孟妍,等. 基于Morlet小波变换的滚动轴承早期故障特征提取研究[J]. 仪器仪表学报, 2013, 34(4): 920-926.

MA Lun, KANG Jianshe, MENG Yan, et al. Research on feature extraction of rolling bearing incipient fault based on morlet wavelet transform[J]. Chinese Journal of Scientific Instrument, 2013, 34(4): 920-926.

[13] QIU H, LEE J, LIN J, et al. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics[J]. Journal of Sound and Vibration, 2006, 289(4/5): 1066-1090.

[14] 唐贵基, 王晓龙. 自适应最大相关峭度解卷积方法及其在轴承早期故障诊断中的应用[J].中国电机工程学报,2015,35(6): 1436-1444.

TANG Guiji, WANG Xiaolong. Adaptive maximum correlated kurtosis deconvolution method and its application on incipient fault diagnosis of bearing [J]. Proceedings of the Chinese Society for Electrical Engineering, 2015, 35(6): 1436-1444.