考虑重力影响的压电悬臂梁发电系统动力学特性研究

杨倩倩， 刘丽兰

(西安理工大学 机械与精密仪器工程学院，西安 710048)

近年来随着微电子技术的发展，传感器的低功耗运行成为可能，从而也促进了传感器自供电技术的快速发展[1-2]，收集环境振动能量并转化为电能已成为一种趋势[3]。压电发电因其结构简单、清洁环保、易于实现微小化等优点越来越广泛地受到大家的关注[4-6]。

由于大多数实际振动环境是随机、多频、时变的，而线性系统的共振频带非常窄[7-8]。在非线性系统中，双稳态系统具有较宽的响应频带，并可以在周期或随机激励下产生大幅运动或混沌运动，显著增加发电能力，所以非线性双稳态压电发电系统越来越受到研究者的注意[9-11]。Erturk等[12]使用数值积分法比较了双稳态压电收集系统中模拟数据和测量数据的线性相似性，并发现了在宽频范围内，双稳态压电发电系统较线性系统可以产生较高的输出功率。Stanton等[13]应用谐波平衡法分析预测了参数变化对双稳态系统稳定性的影响，并采用数值模拟和实验验证的方式对双稳态压电发电系统进行了分析，为此后实验的操作提供了理论上的依据。Guo等[14]使用哈密顿原理建立了双稳态压电悬臂梁发电系统的压电—磁—弹性耦合的分布参数模型，研究了磁体间距对于系统静态分岔特性的影响，以及不同外部激励对电输出特性的影响。Singh等[15]提出了双稳态传感器的精确模型，即在非线性提取电路中使用同步电荷提取(Synchronous Charge Extraction， SCE)和电感器上的并行同步开关采集(Synchronized Switch Harvesting on Inductor， SSHI)，可以显著提高俘能效率。

在压电发电系统方面虽然出现了大量研究成果，但上述研究多假设在理想实验条件下，未考虑重力对系统的影响。鉴于此，本文建立了考虑重力影响的压电悬臂梁发电系统的力学模型，研究了简谐和白噪声激励下，重力对系统输出功率的影响规律，并结合半功率带宽法，首次提出了白噪声激励下重力最小影响区间的确定方法。

1 压电悬臂梁发电系统模型

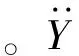
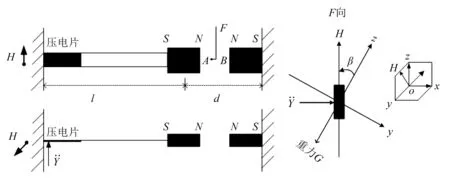
图1 压电悬臂梁发电系统结构简图Fig.1 Structure diagram of piezoelectric cantilever beam power generation system

根据图1，得到压电悬臂梁发电系统的力学模型，如图2所示。

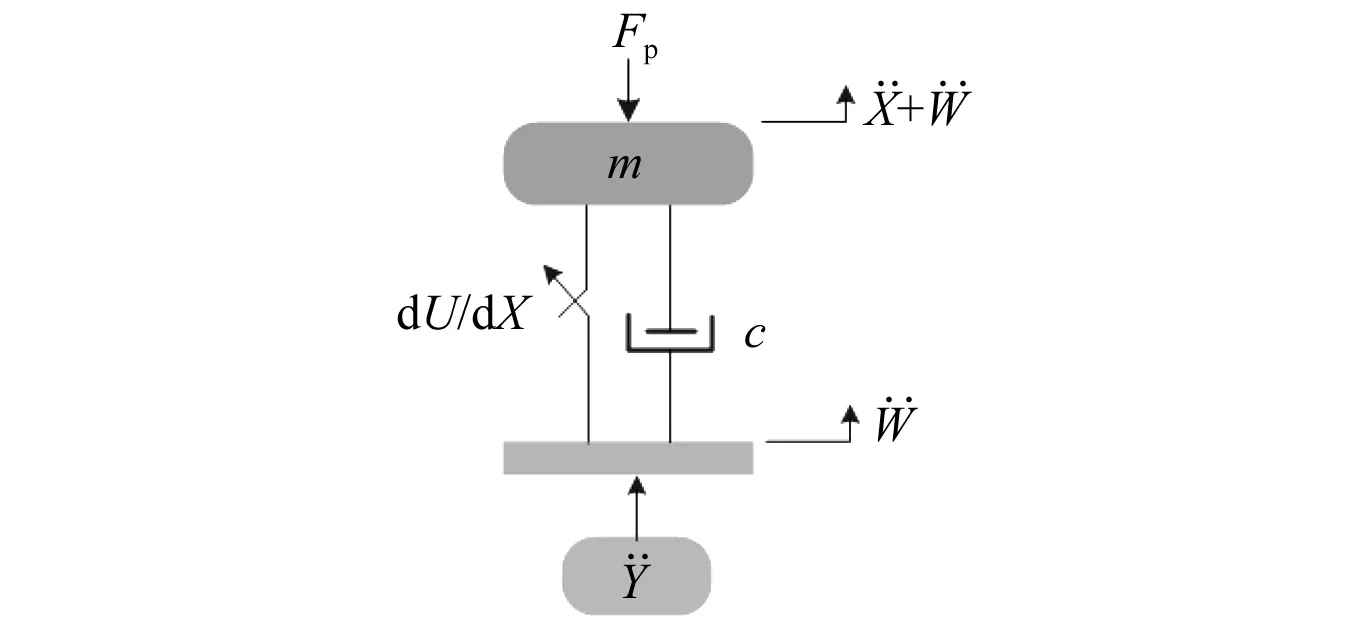
图2 压电悬臂梁发电系统的力学模型Fig.2 Mechanical model of piezoelectric cantileverbeam power generation system

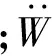
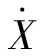
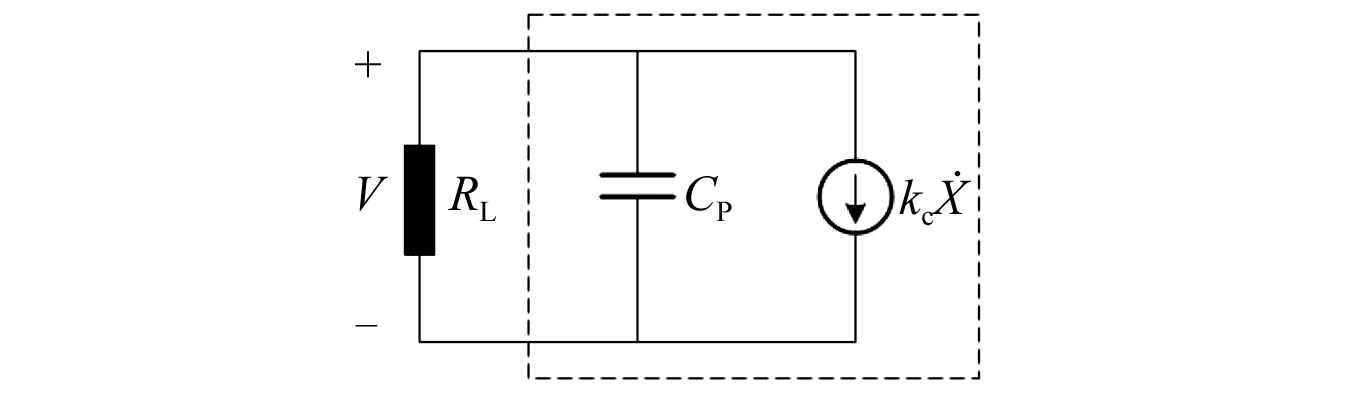
图3 压电悬臂梁电路分析等效模型Fig.3 Equivalent model of circuit analysis for piezoelectric cantilever beam

根据图2和图3，得到系统的控制方程和电学方程为

(1)

式中：X为质量块的相对位移；Fr为磁力函数在平行于yz平面且垂直于H方向的分量；k为悬臂梁的弹性系数。

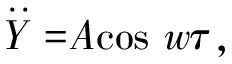
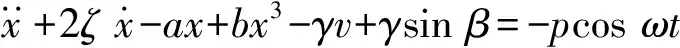
(2)

其中，

ζ=c/(2mv)
a=(3μ0MBVBMAVA)/(2πkd4l)-1
b=3μ0MBVBMAVAl(1/l2+5/d2)/(2πkd4)
γ=mg/(kl),p=mA/(kl)
μ=1/(RLCpv), ϑ=kcl/(Cpe)
ω=w/v

(3)

且MA,MB分别为磁铁A和B的磁化强度；VA,VB分别为磁铁A和B的体积；μ0=4π×10-7H/m 为真空磁导率；d为两磁铁中心之间的水平距离；l为磁铁A中心到梁根部的距离；kc，kV分别为与电压相关的耦合系数和电压耦合系数。

2 势能函数

根据无量纲方程式(2)可知

dU/dx=-ax+bx3+γsinβ

(4)

得出系统势能函数为

(5)

参数取a=9.6,b=2,γ=5, 势能函数随着偏转角度β变化的三维曲面图如图4所示。

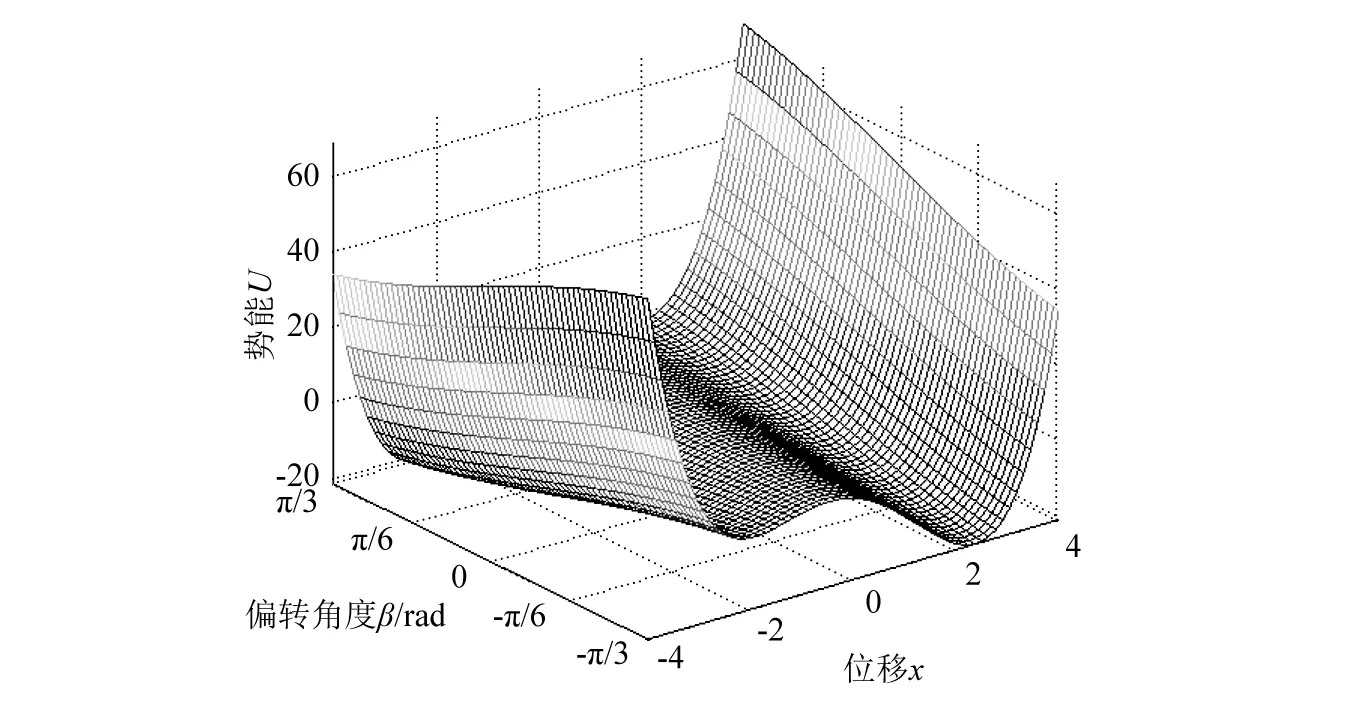
图4 势能函数随偏转角度变化三维图Fig.4 The potential function changes with the deflection angle

从图4中可以看出，势能函数在x<0和x>0部分变化趋势正好相反。当x<0时，曲面随着β的增大呈现下降趋势，而当x>0时，曲面随着β的增大呈现上升的趋势。

为方便研究势能函数不对称性规律，分别取β为-π/3，-π/6，0，π/6，π/3。不同β下势能函数随着相对位移x的变化情况如图5所示。

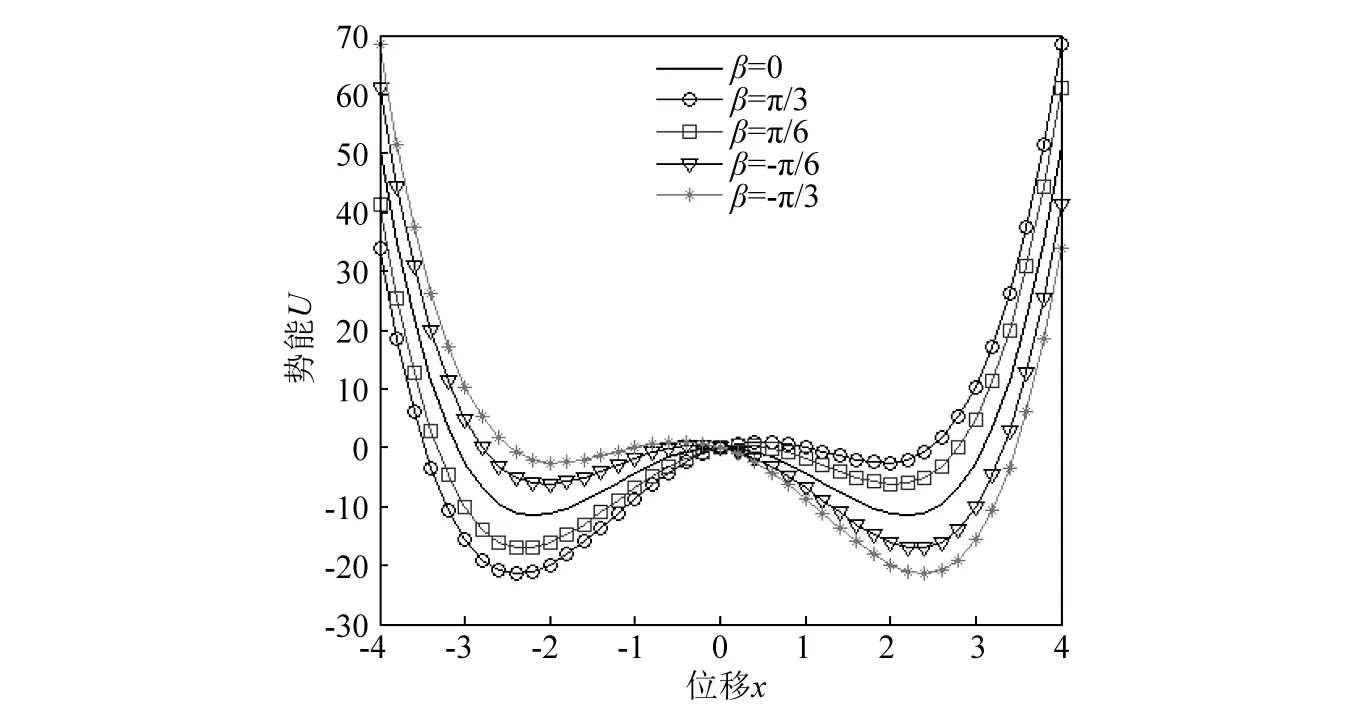
图5 偏转角度β对势能函数的影响Fig.5 Influence of deflection angle β on potential energy function

从图5可以看出，当β=0时，即不考虑重力的情况下，势能函数为对称状态。随着β的变化，势能函数曲线呈现出不同的非对称状态，但势垒仍在x=0点。当β从0增大到π/3时，左侧势阱变深，右侧变浅，从0减小到-π/3时情况正好相反，即随着的逐渐增大，左侧势阱变浅，右侧势阱变深。

3 数值仿真

3.1 简谐激励

3.1.1 相图和频谱图

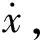
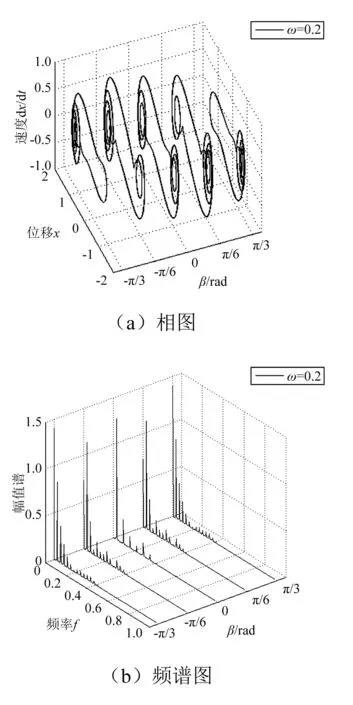
图6 ω=0.2时的相图和频谱图Fig.6 The phase diagrams and spectrums of ω=0.2

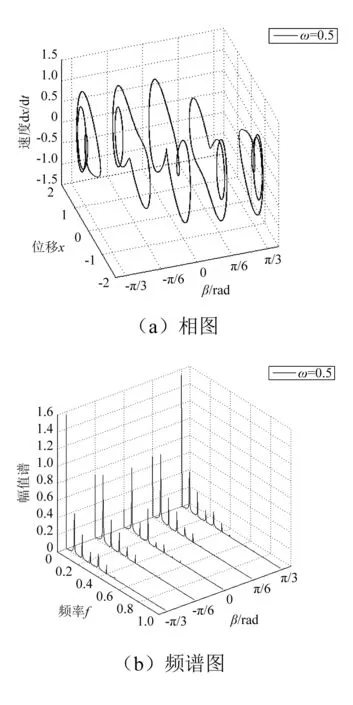
图7 ω=0.5时的相图和频谱图Fig.7 The phase diagrams and spectrums of ω=0.5

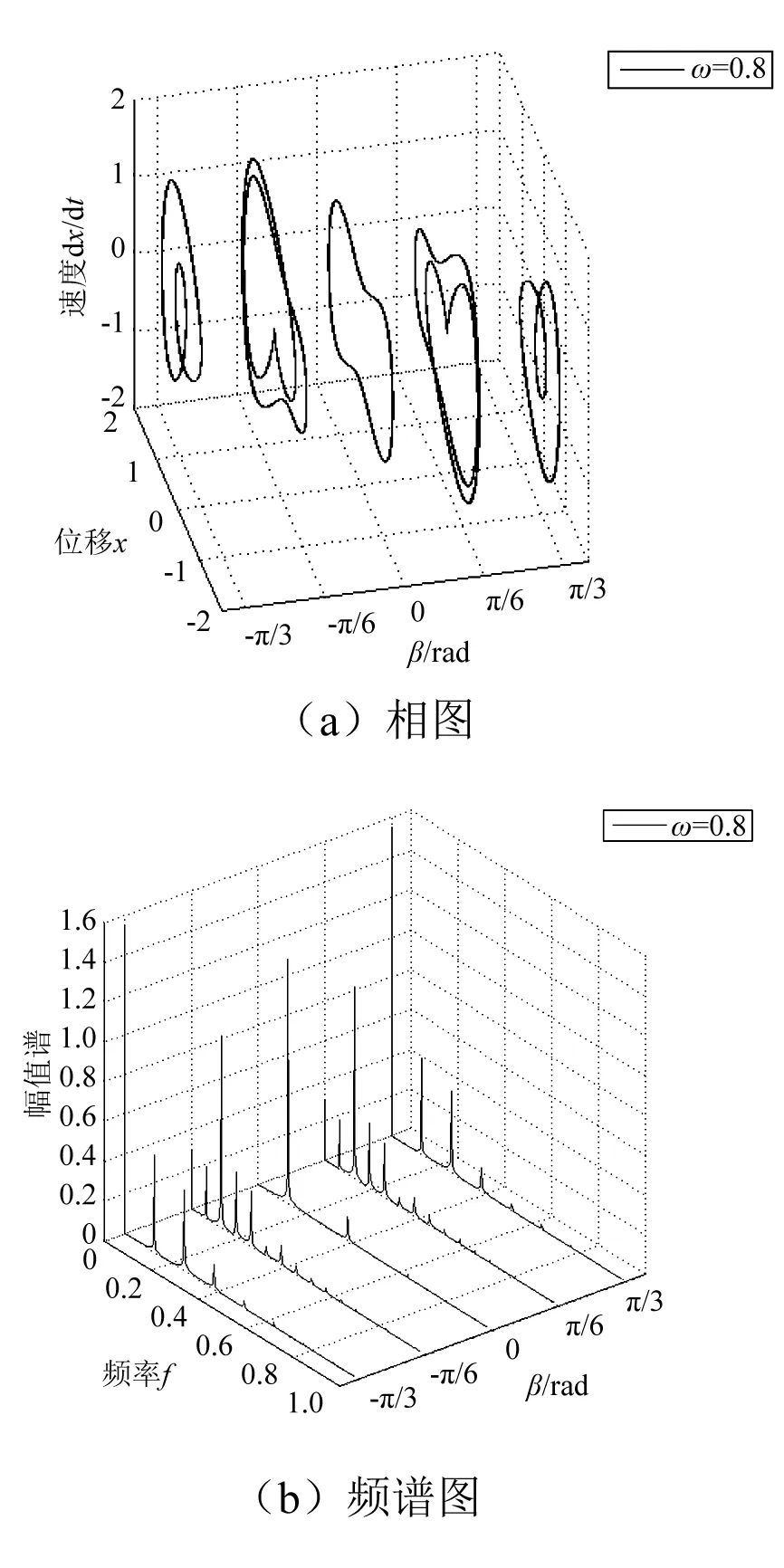
图8 ω=0.8时的相图和频谱图Fig.8 The phase diagrams and spectrums of ω=0.8

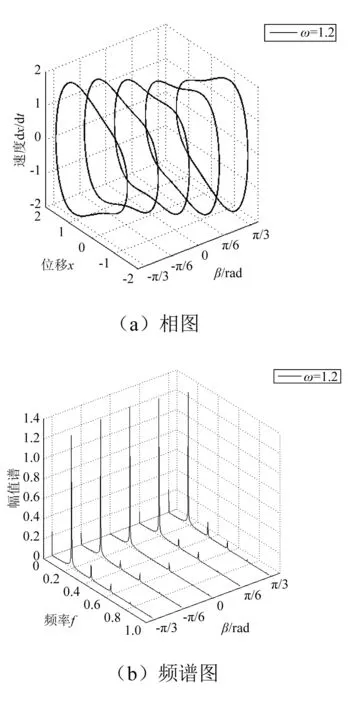
图9 ω=1.2时的相图和频谱图Fig.9 The phase diagrams and spectrums of ω=1.2

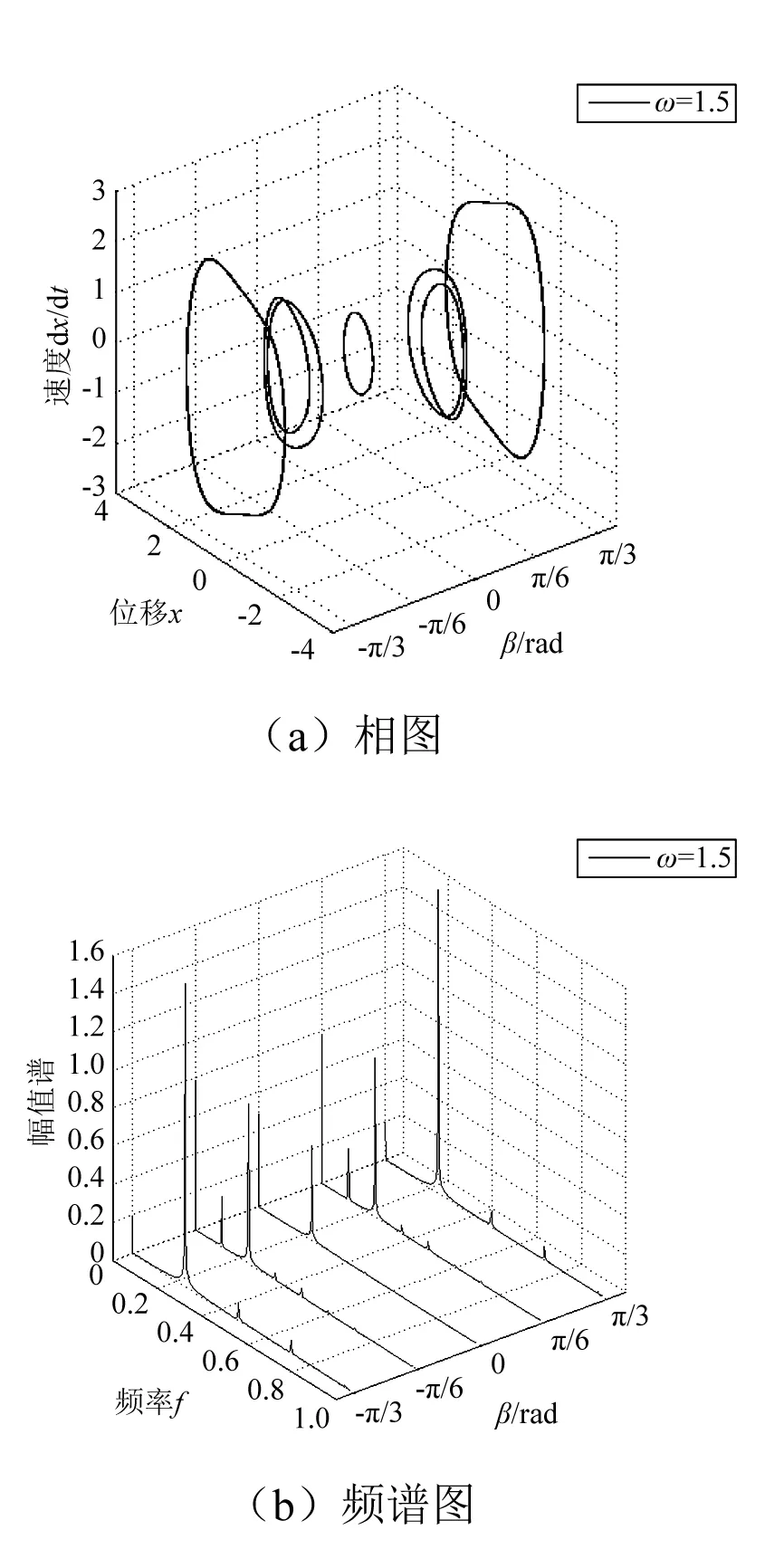
图10 ω=1.5时的相图和频谱图Fig.10 The phase diagrams and spectrums of ω=1.5

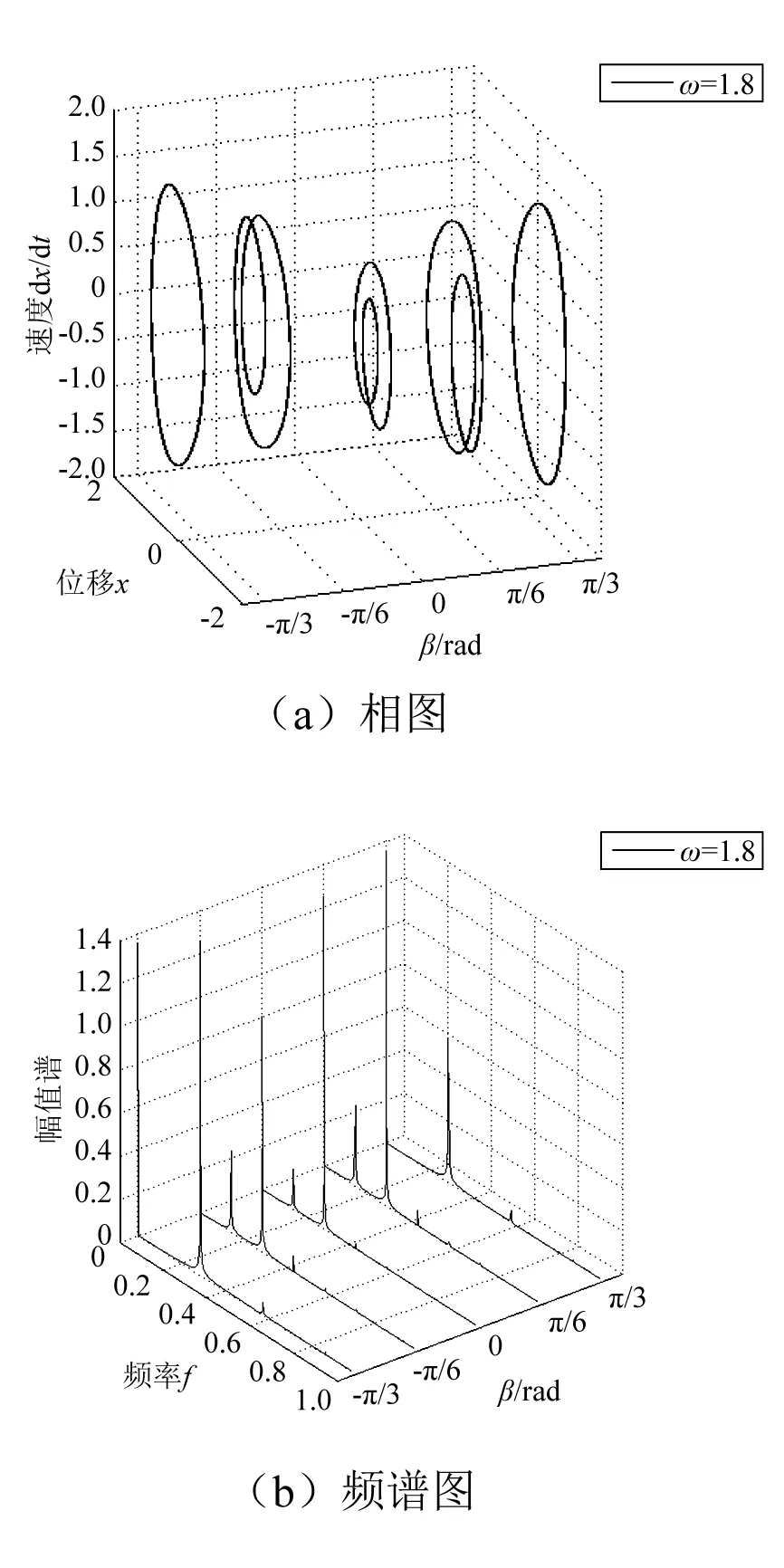
图11 ω=1.8时的相图和频谱图Fig.11 The phase diagrams and spectrums of ω=1.8

图6中ω=0.2时，β在[-π/3, π/3]内系统均可以跨越势垒做大幅混沌运动。逐渐增大激励频率，如图7所示，当ω=0.5时，系统在β=-π/3和π/3时变为小幅运动，在β=-π/6，π/6和0时仍做大幅运动。当ω增大到0.8时，系统在β=0变为大幅周期运动，其余角度运动状态不变，如图8所示。继续增大ω，当ω=1.2时，系统在β∈[-π/3, π/3]范围内均做大幅周期运动，如图9所示。当激励频率ω增大到1.5时，系统在β=0时为小幅周期运动，在β=-π/6和π/6时产生两倍亚谐共振，而在β=-π/3和π/3时仍为大幅周期运动，如图10所示。继续增大激励频率，当ω=1.8时，系统在β=-π/6，π/6和0时做两倍亚谐共振，在β=-π/3和π/3时为小幅周期运动，如图11所示。

从图6～图11可以看出，当偏转角度β=0时，随着外部激励频率的增加，系统的运动变化过程为：混沌运动-大幅周期运动-小幅周期运动-两倍亚谐共振。在β=-π/6，π/6时，系统运动状态变化过程为：混沌运动-大幅周期运动-两倍亚谐共振。在β=-π/3和π/3时，系统的运动变化过程为：混沌运动-小幅运动-大幅周期运动-小幅周期运动。所以重力的影响会导致系统的运动状态发生变化，且重力不同，对系统状态的影响也不同。

综合上述可以看出：①当激励频率小于1.2时，重力对系统的大幅运动响应产生了较大影响，由大幅周期运动变成了某个平衡点上的小幅周期或者小幅混沌运动；②当外部频率增大到1.5和1.8时，重力的影响反而有利于系统产生大幅运动，如在1.5时，β在-π/3和π/3两个角度下系统产生了大幅周期运动，此时不受重力影响的双稳态系统反而出现了小幅周期运动。在外部激励频率为1.8时，不管是系统是否受重力影响，双稳态系统均表现为小幅周期运动，但受重力影响的双稳态系统的小幅周期运动幅值也大于不受重力影响的系统的响应幅值。

3.1.2 输出功率

由于压电悬臂梁发电系统主要收集环境中的机械振动，并将其转化为电能[16-17]。研究系统输出功率可以更方便地了解系统的发电性能，并通过结合时域图、相图和频谱图等，可以更全面地对系统响应进行分析。系统的输出功率可以用P=μ·v2来表示。图12(a)给出了不同外部激励频率和β角下，运动悬臂梁发电系统的输出功率。

为了更方便研究重力对发电功率的影响程度，设重力影响因子ψ=(Pβ-P0)/P0，其中Pβ为某一激励频率下β所对应的输出功率，P0为β=0时所对应的输出功率。结合图12(a)并通过计算分析，当ω从0.2增大到1.8时，β所对应的影响因子如图12(b)所示。由于图12(a)中不同激励频率下的系统输出功率关于β=0大体呈对称状态，所以图12(b)仅给出了β∈[-π/2, 0]时的重力影响因子变化情况。

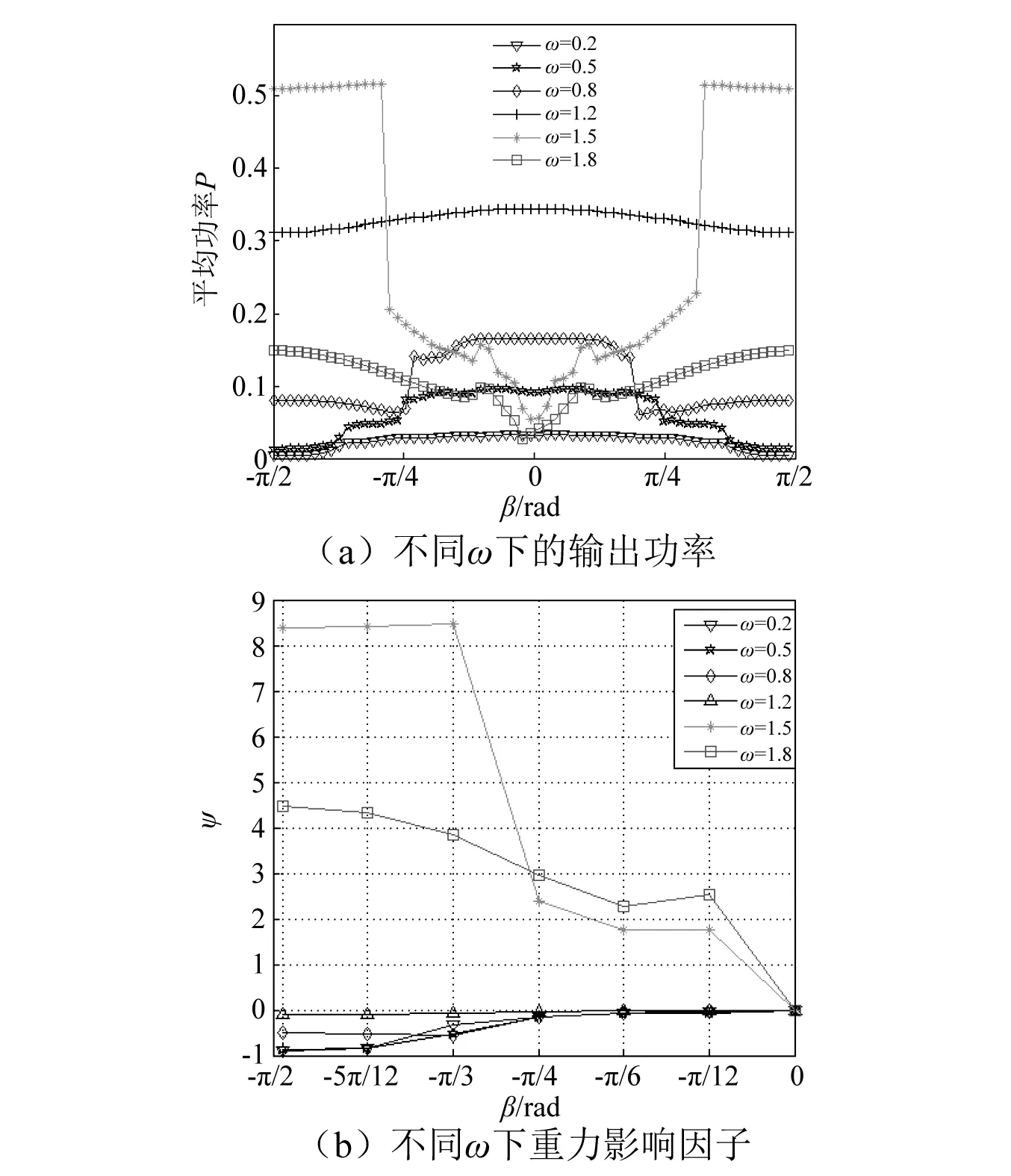
图12 不同激励频率下的平均输出功率和重力影响因子Fig.12 Average output power and gravity influence factor under different ω

从图12(b)中可以看出，当ω(0.2≤ω≤1.8)取某一固定值时，随着|β|的增大，|ψ|也随之增大，即偏转角度越大，重力对系统输出功率的影响越大。

当0.2≤ω≤1.2时，ψ≤0，重力对输出功率表现为削弱作用，结合图12(a)可以看出，当ω从0.2逐渐增大到1.2时，系统输出功率大体呈现上升趋势，即在低频环境下，激励频率越大，系统发电性能越好，且随着ω的增大，某一偏转角度β所对应的|ψ|越小，即激励频率的增大也会削弱重力对系统输出功率的影响。

当β∈[-π/4, π/4]时，在ω从1.2增大到1.8的过程中，系统的输出功率大体呈现减小趋势，且系统在无重力影响即β=0时递减最快。当系统有重力影响即β≠0时递减较慢，且重力影响越大，输出功率递减相对越慢。所以当系统的激励频率足够大时，随着激励频率的增大，系统输出功率逐渐减小，重力的作用会使这种减弱趋势变慢。

综上所述，系统在低频激励下，发电功率随着激励频率的增大而增大，重力的影响会减弱系统的发电功率。但是当激励频率足够大时，系统的发电功率随着激励频率的增大而减小，重力的影响会使系统的发电功率下降较慢。

3.2 高斯白噪声激励

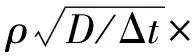
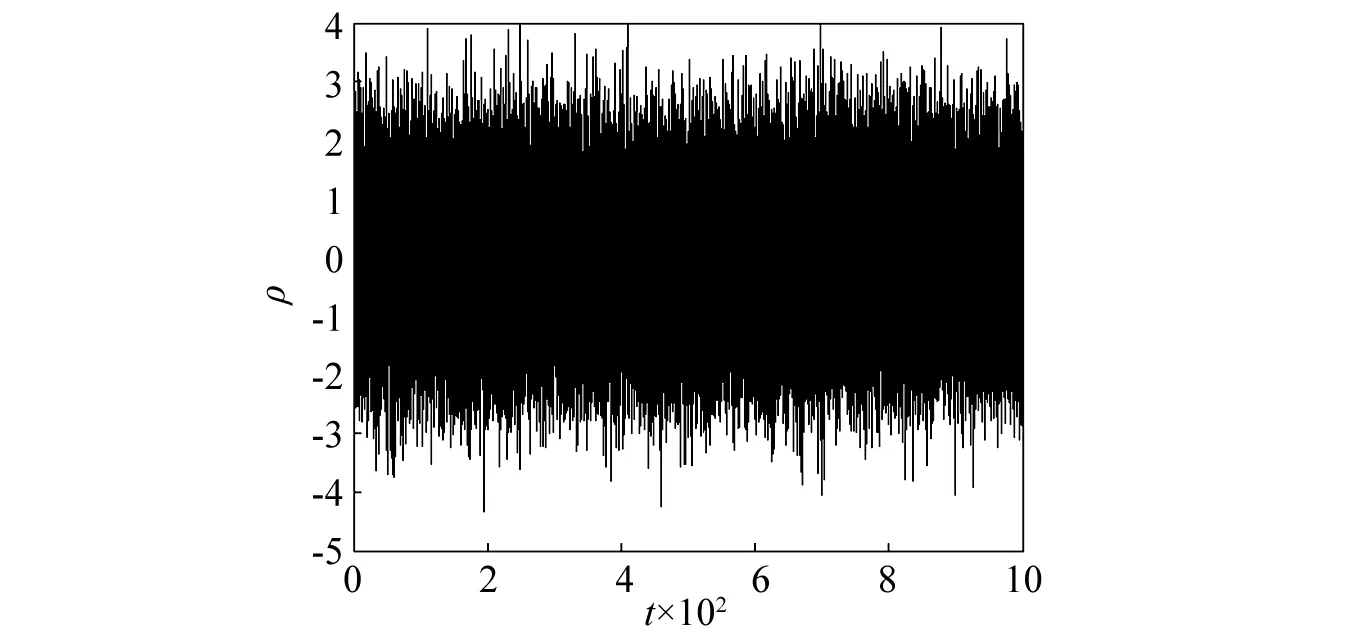
图13 模拟的高斯白噪声信号Fig.13 Simulation of Gaussian white noise signal

参照简谐激励下系统的动力学模型，高斯白噪声下动力学模型的无量纲方程可写为

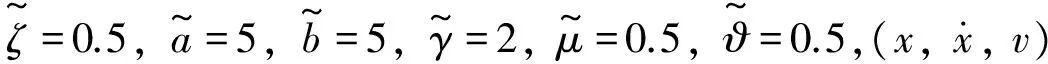
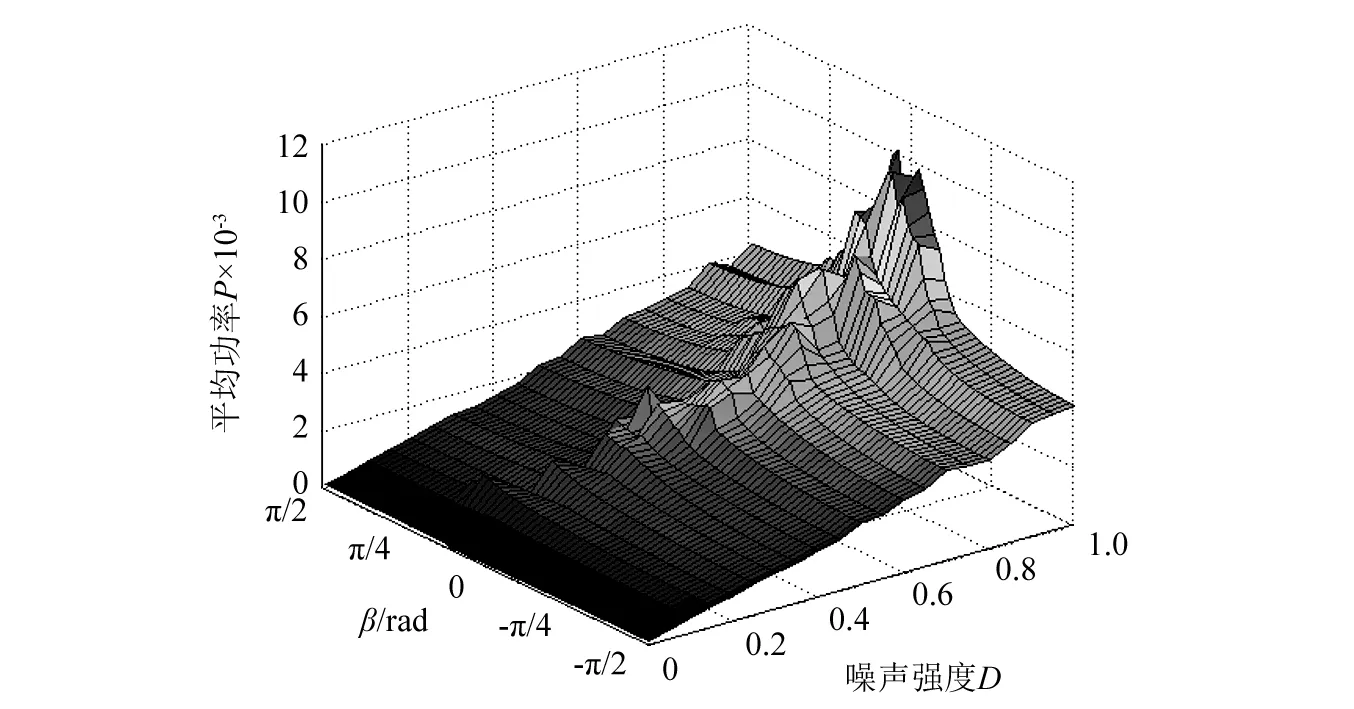
图14 不同噪声强度下的平均功率图Fig.14 Average power at different noise intensities

从图14可以看出，噪声强度很小时，系统的发电能力很微弱，且平均输出功率几乎不受β影响。随着噪声强度的不断增大，系统得到的能量也不断增大，平均功率越来越大，且在β=0附近的一个范围内达到最大。根据能量守恒可知，外部激励给系统传递能量时，一部分能量需要克服重力做功，故系统的平均功率会变小，发电能力变弱。

为了说明问题方便，分别选取D为0.2，0.5，0.7，1.0时平均输出功率随着偏转角度的变化的二维关系曲线，如图15所示。

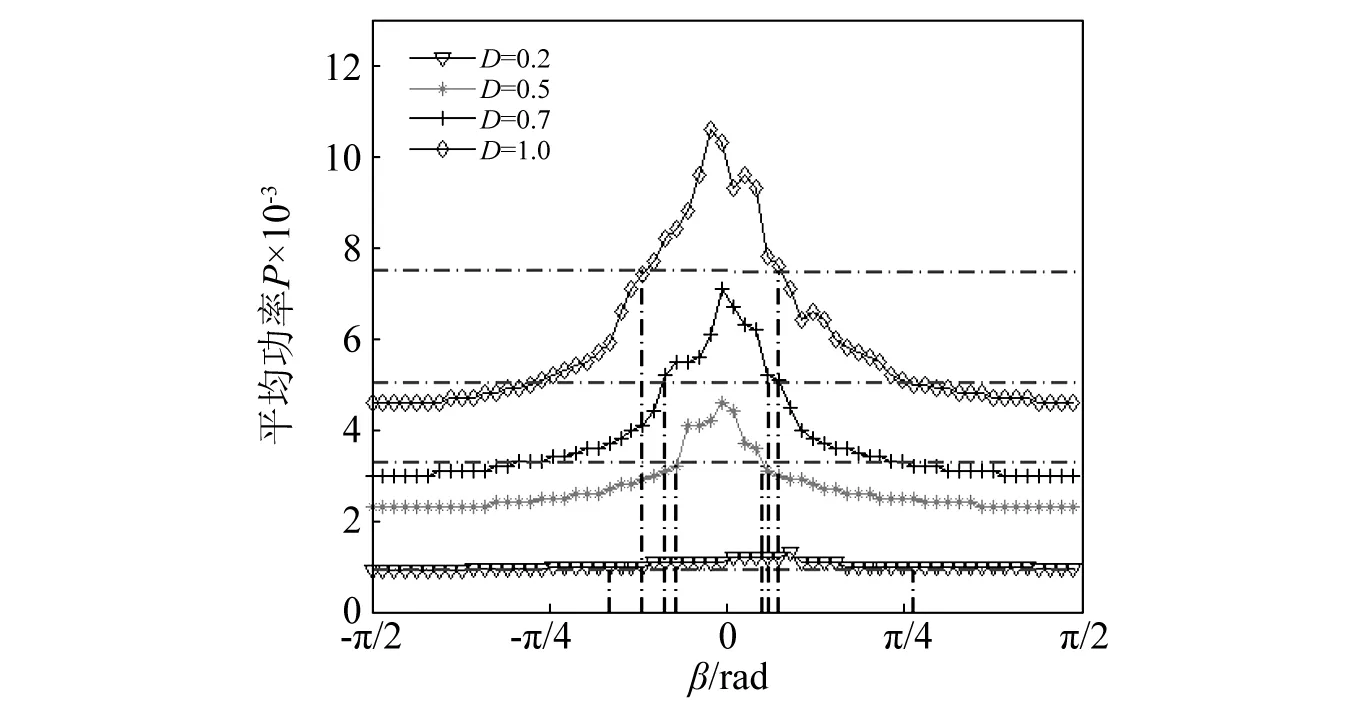
图15 不同噪声强度下的功率曲线Fig.15 Power curve at different noise intensity

从图15可以看出，随着噪声强度D的增加，系统总体的输出功率也在增大。在β=0时，即不考虑重力的影响时，系统的平均输出功率最大；β≠0时系统的输出功率小于β=0时，且随着|β|的增大，输出功率也越小。

虽然重力对系统的输出功率有影响，但在一定的影响范围内系统仍具有良好的发电性能，仍可以被接受。为了确定不同噪声强度下可接受的输出功率，本

为了检验所提出半功率法确定最小影响区间的有效性，图15～图18分别给出了当D为0.2，0.5，0.7，1.0时最小影响区间上两个极限端点和零值时系统的位移时域图和相图。

从图16可以看出，在噪声强度很小时，例如D=0.2时，系统在任何偏转角度下均只做小幅运动。当噪声强度足够大时(例如当D=0.5，0.7和1.0时)，如图17～图19所示，在不同的噪声强度下，在可接受区域的两个端点(即此范围内重力影响最大的两个位置)，压电悬臂梁系统在两个平衡点间仍然保持大幅混沌运动，输出较大功率，但平衡点上混沌运动的振幅出现了大小不等，也反映出重力的确对系统的大幅运动振幅存在影响。

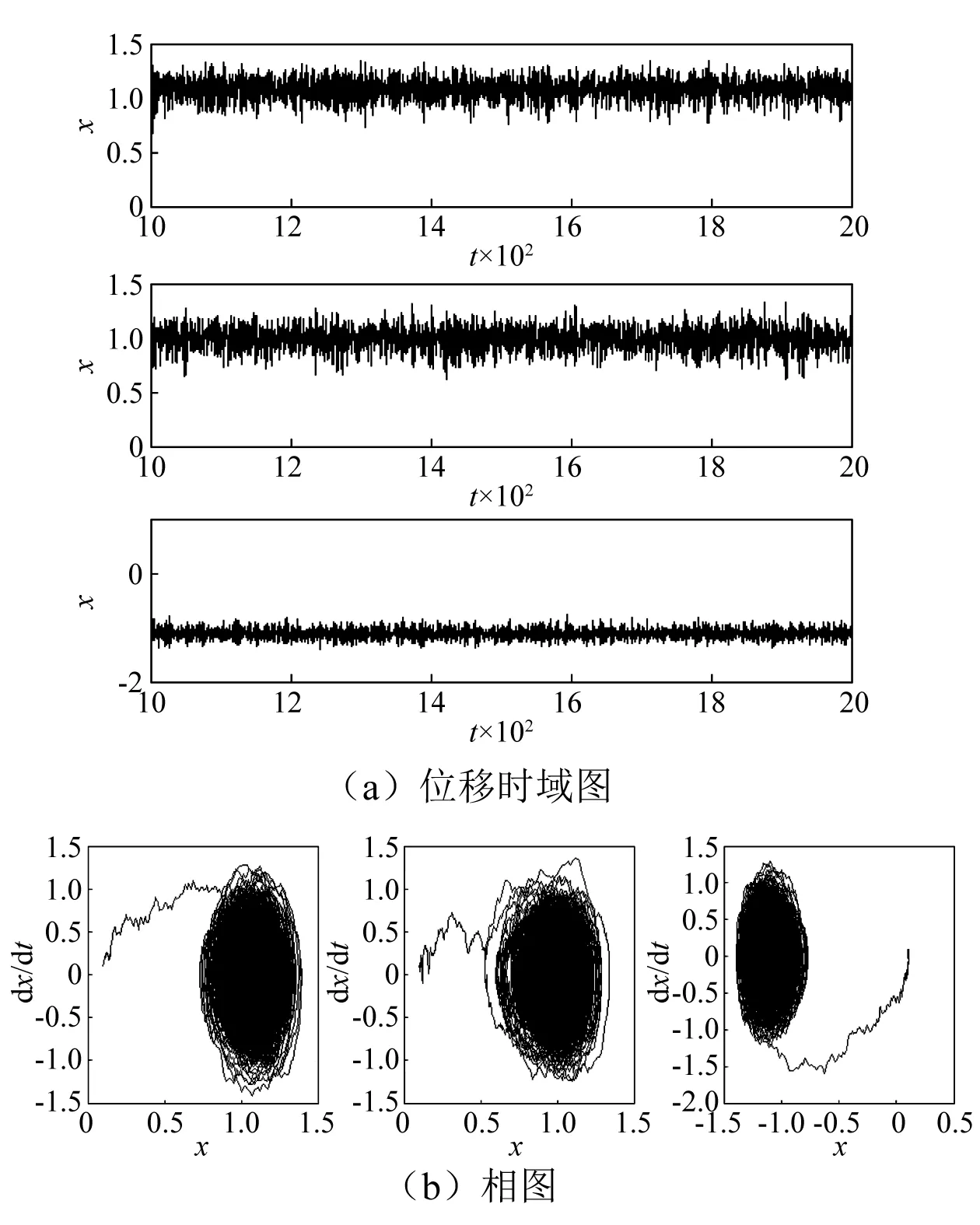
图16 D=0.2时系统分别在最小影响区间左端点、零点和右端点时的位移时域图和相图Fig.16 The time-domain and phase diagrams of the system at the left end point, zero point and right end point of the minimum influence interval when D=0.2

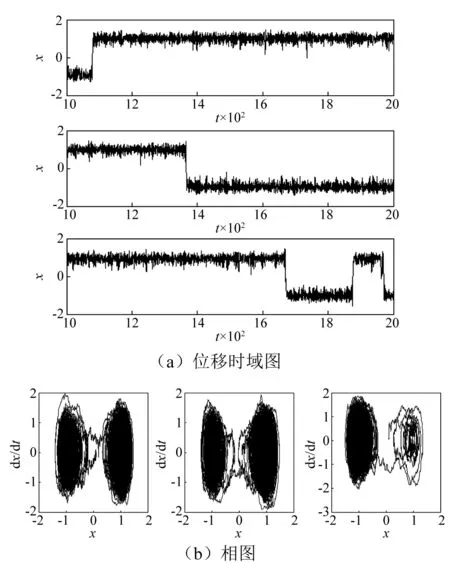
图17 D=0.5时时系统分别在可接受区左端点、零点和右端点时的位移时域图和相图Fig.17 The time-domain and phase diagrams of the system at the left end point, zero point and right end point of the minimum influence interval when D=0.5

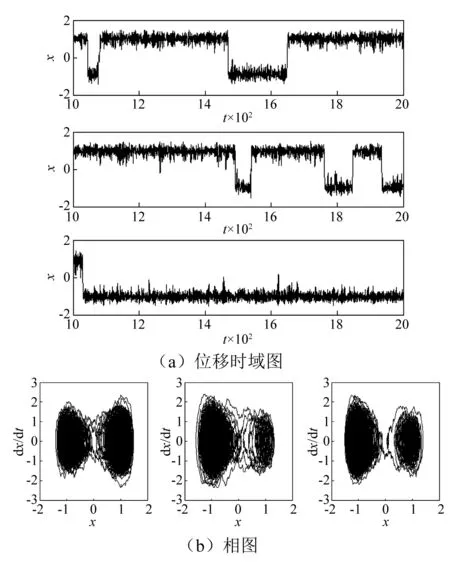
图18 D=0.7时时系统分别在可接受区左端点、零点和右端点时的位移时域图和相图Fig.18 The time-domain and phase diagrams of the system at the left end point, zero point and right end point of the minimum influence interval when D=0.7

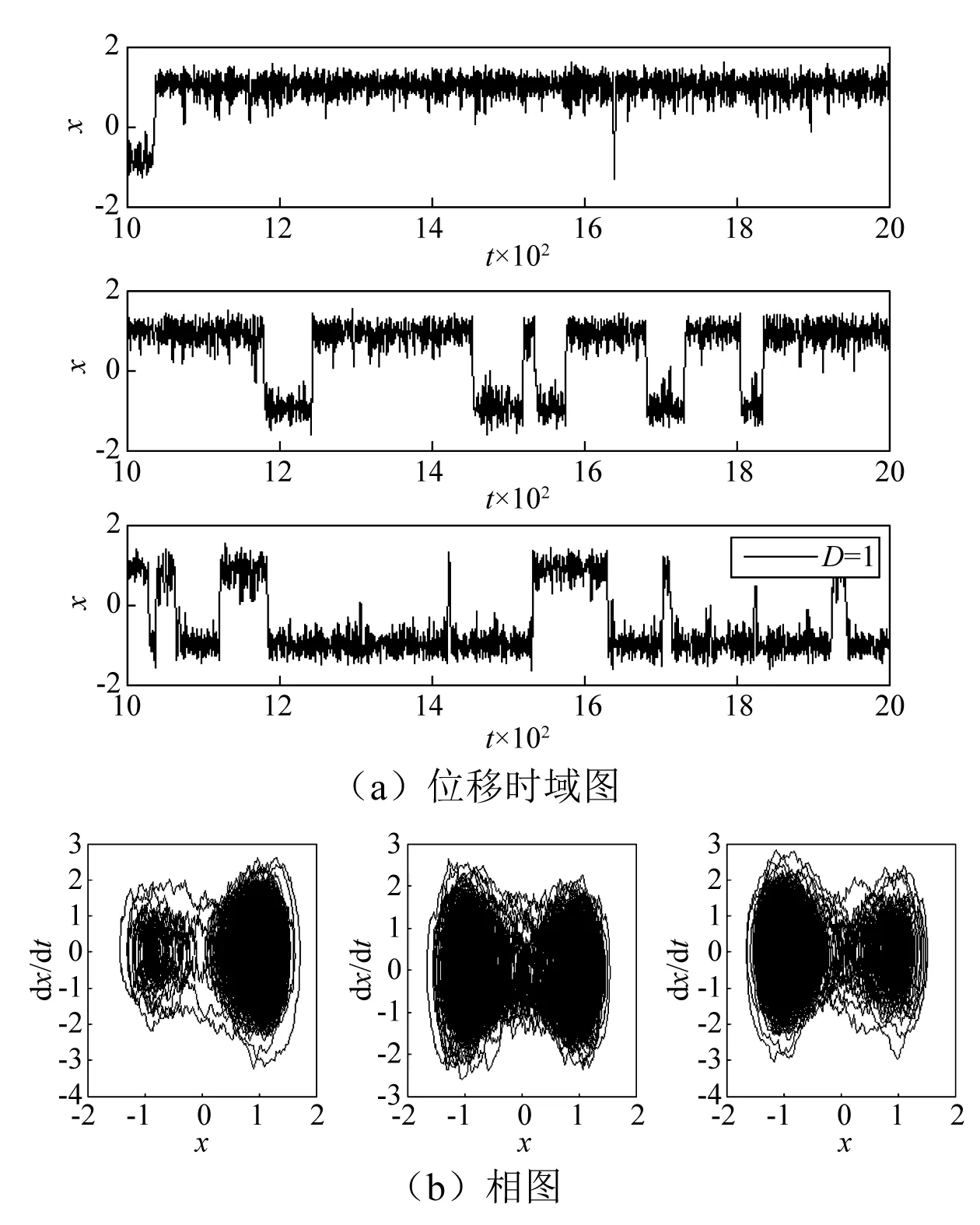
图19 D=1.0时时系统分别在可接受区左端点、零点和右端点时的位移时域图和相图Fig.19 The time-domain and phase diagrams of the system at the left end point, zero point and right end point of the minimum influence interval when D=1.0

4 结 论

本文建立了考虑重力影响的压电悬臂梁发电系统的力学模型及其控制方程。从数值仿真的角度分别研究了在简谐激励和随机激励下重力对系统的动力学特性和发电功率的影响。主要结论如下：

(1)重力的影响会使系统的势能函数出现不对称性，当β从0增大到π/3时，左侧势阱变深，右侧变浅，从0减小到-π/3时情况正好相反，即随着β的逐渐增大，左侧势阱变深，右侧势阱变浅。

(2)简谐激励时，当激励频率小于1.2时，重力对系统的大幅运动响应产生了较大影响，由大幅周期运动变成了某个平衡点上的小幅周期或者小幅混沌运动，重力的影响会减弱系统的发电功率；当外部频率增大到1.5或者1.8时，重力的影响反而有利于系统产生大幅运动或者较大的小幅周期运动。

(3)白噪声激励时，系统的输出功率随着噪声强度的增大出现了整体增大的趋势，随着|β|角度的增大，即重力影响的增大，系统的输出功率出现了逐渐下降的趋势。借助半功率带宽法思想，在系统发电功率变化可接受的前提下，得到重力最小影响区间，获得了偏转角度β变化的最大可接受区间。

[ 1 ] TANG X, ZUO L. Enhanced vibration energy harvesting using dual-mass systems[J]. Journal of Sound & Vibration, 2011, 330(21): 5199-5209.

[ 2 ] BILGEN O, FRISWELL M, ALI S F, et al. Broadband vibration energy harvesting from a vertical cantilever piezocomposite beam with tip mass[J]. International Journal of Structural Stability & Dynamics, 2015, 15(2): 197-421.

[ 3 ] PERTON M, AUDOIN B, PAN Y D, et al. Energy harvesting vibration sources for microsystems applications[J]. Measurement Science & Technology, 2006, 17(12): 175-

195.

[ 4 ] TSUJIURA M. Piezoelectric ceramic element for power generation and method: US 20050211948 A1 [P]. 2005.

[ 5 ] MAK K H, MCWILLIAM S, POPOV A A, et al. Performance of a cantilever piezoelectric energy harvester impacting a bump stop[J]. Journal of Sound & Vibration, 2011, 330(25): 6184-6202.

[ 6 ] CHEN N, JUNG H J, JABBAR H, et al. A piezoelectric impact-induced vibration cantilever energy harvester from speed bump with a low-power power management circuit[J]. Sensors & Actuators A Physical, 2016, 254: 134-144.

[ 7 ] STANTON S C, MCGEHEE C C, MANN B P. Nonlinear dynamics for broadband energy harvesting: investigation of a bistable piezoelectric inertial generator[J]. Physica D Nonlinear Phenomena, 2010, 239(10): 640-653.

[ 8 ] BURROW S G. Vibration energy harvesters with non-linear compliance[C]∥ Proceedings of SPIE-The international

Society for Optical Engineering. San Diego: Active and Passive Smart Structures and Integrated Systems, 2008.

[ 9 ] PELLEGRINI S P, TOLOU N, SCHENK M, et al. Bistable vibration energy harvesters: a review[J]. Journal of Intelligent Material Systems & Structures, 2013, 24(11): 1303-1312.

[10] 白凤仙, 马桂帅, 董维杰, 等. 悬臂梁式压电振动能量收集系统输出功率的优化研究[J]. 电子学报, 2014, 42(5): 883-889.

BAI Fengxian, MA Guishuai, DONG Weijie, et al. Optimization of the output power of cantilever piezoelectric vibration energy harvesting[J]. Acta Electronica Sinica, 2014, 42(5): 883-889.

[11] MASANA R, DAQAQ M F. Relative performance of a vibratory energy harvester in mono-and bi-stable potentials[J]. Journal of Sound & Vibration, 2011, 330(24): 6036-

6052.

[12] ERTURK A, INMAN D J. Broadband piezoelectric power generation on high-energy orbits of the bistable duffing oscillator with electromechanical coupling[J]. Journal of Sound & Vibration, 2011, 330(10): 2339-2353.

[13] STANTON S C, OWENS B A M, MANN B P. Harmonic balance analysis of the bistable piezoelectric inertial generator[J]. Journal of Sound & Vibration, 2012, 331(15): 3617-

3627.

[14] GUO K, CAO S, WANG S. Numerical and experimental studies on nonlinear dynamics and performance of a bistable piezoelectric cantilever generator[J]. Shock & Vibration, 2015(21): 1-14.

[15] SINGH K A, KUMAR R, WEBER R J. A broadband bistable piezoelectric energy harvester with nonlinear high-power extraction[J]. IEEE Transactions on Power Electronics, 2015, 30(12):6763-6774.

[16] SAADON S, SIDEK O. Vibration-based MEMS piezoelectric energy harvester (VMPEH) modeling and analysis for green energy source[C]∥ Developments in E-Systems Engineering. Dubai: IEEE, 2011:527-531.

[17] RAM G D, PRAVEENKUMAR S. PVDF polymer-based MEMS cantilever for energy harvesting[M]∥Artificial Intelligence and Evolutionary Computations in Engineering Systems. New Delhi: Springer, 2016: 917-923.