基于HMM和优化的PF的数控转台精度衰退模型

王 刚， 陈 捷,2， 洪荣晶,2， 王 华,2

(1.南京工业大学 机械与动力工程学院，南京 211800；2. 江苏省工业装备数字制造及控制技术重点实验室，南京 211800)

数控转台是高档数控机床的重要功能部件，数控转台的分度精度和重复定位精度对数控机床的加工精度具有重要影响[1]。在数控机床中转台处于加工区域，工作环境恶劣，容易导致精度的过快衰减。已有的测量精度方法过于繁琐，且在很多情况下限于环境因素难以测量。因此，找到一种以描述数控转台精度衰减为核心的建模方法不失为一种新的尝试。目前，建模思路主要分为两种[2]，一种是根据数控转台的物理结构建立数学模型；Yu等[3]分析了一种大型数控转台的电液耦合的动态特性，并且认为数控转台蜗轮传动系统的综合反向间隙是影响分度精度和动态特性的关键因素之一；然而，建立一个能准确且全面地反映数控转台的精度变化的数学模型十分困难；另一种是通过智能算法在振动信号等数据驱动的基础上建立模型[4]，与数学模型相比智能算法不需要分解数控转台的结构，而是通过振动信号等数据作为观察值，对蕴含在数据中的反应数控转台状态变化的信息进行发掘，从而转化为对数控转台状态的评价。Benkedjouh等[5]使用小波变换进行降噪和提取特征向量，运用支持向量机(Support Vector Machine， SVM)建立剩余寿命预测模型。Lu等[6]在大型回转支承的研究中使用小波能量熵(Wavelet Energy Entropy， WEE)和检验模态分解法(Empirical Mode Decomposition， EMD)进行降噪和特征向量提取，使用主成分分析法(Principal Component Analysis， PCA)对多维特征向量进行降维，最后运用最小二乘支持向量机建立了衰退预测模型。然而，数控转台精度变化的趋势信息在转台的振动信号中往往非常微弱，很容易被周围环境产生的白噪声掩盖。Matej等[7]在研究回转支承时运用EEMD-MSPCA(Ensemble Empirical Mode Decomposition Multi-scale Principal Component Analysis)进行降噪并提取特征向量，为解决信号微弱问题提供了思路。在此基础上Feng等[8]进行了改进，建立了EEMD-PCA算法，克服了其在降噪时经验参数难以获得的缺点。除此之外，数控转台的驱动形式、摩擦特性、系统刚度、阻尼因素、消隙预载等众多因素都会影响到其最终的动静态分度精度以及其精度保持性[9]，其中某些因素难以直接观察，因此需要一些更具有针对性的算法。Wang等[10]在研究中将隐马尔科夫(Hidden Markov Model, HMM)方法引入到齿轮箱的寿命预测中，比较有效地识别出某些难以观察到的状态。张西宁等[11]将主分量分析法(PCA)与隐马尔科夫(HMM)结合，用到对轴承的诊断检测中。

针对以上的问题，结合数控转台串联系统的结构特点，利用隐马尔科夫(HMM)算法既可以讨论可观察状态又可以讨论隐藏状态的特点，提出用振动信号训练过的隐马尔科夫(HMM)模型进行精度衰退诊断并建立健康状态指标，以粒子群算法(Particle Swarm Optimization, PSO)优化过的粒子滤波(Particle Filtering, PF)算法作为预测模型计算数控转台精度衰退的剩余寿命，并将优化前后的结果以及其他优化方法的结果进行对比分析。同时，在数控转台精度衰退加速寿命试验过程中使用激光干涉仪定期测量转台的重复定位精度，以验证该模型的有效性。

1 构建数控转台精度衰退预测模型

1.1 隐马尔科夫(HMM)算法

隐马尔科夫算法是建立在马尔科夫假设、不动性假设和输出独立性假设的基础上。其核心思想是通过可观察到的状态来推断出隐藏状态。对HMM有下面五个参数来表述[12]：马尔科夫链的状态数N；每种状态对应的观察值的数目M；状态转移概率矩A={αij}；在状态j时的观察概率分布B={βj(k)}；初始状态概率分布v={vi}。HMM的表达式可以简写成λ=(A,B,v)。

在使用HMM建立观察序列的模型时通常使用三种算法来解决三个基本的问题[13]：前向-后向算法解决评估问题，即已知观察序列和概率模型，计算观察序列的概率值P(O|λ)。Viterbi算法解决解码问题，即已知观察序列和概率模型，找到一个最可能的隐藏状态序列S。Baum-Welch算法解决学习问题，即通过已知的观察序列建立最有可能的HMM模型。

本文使用对精度变化敏感的若干统计特征量组成观察矩阵OB作为观察值序列，人为设置了四个隐藏状态，训练一个HMM模型。再使用训练过的模型进行精度衰退的早期诊断。与以往使用HMM算法进行状态识别不同的是，本文在进行早期诊断的过程中，使用HMM算法将数控转台的正常精度状态与后面变化的精度状态作比较，得出的是各个精度状态下的精度与正常状态下的精度的匹配程度，由此建立数控转台精度衰退的健康状态指标H。

1.2 粒子滤波算法(PF)

(1)

在建立粒子滤波算法预测数控转台精度变化的过程中，首先要建立其状态空间模型方程。在已有的健康指标H的基础上，使用高斯函数对H进行非线性回归拟合，得到拟合的状态空间模型[15]

(2)

(3)

(4)

(5)

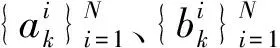
(6)

(7)

(8)

(9)

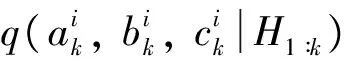
1.3 粒子群(PSO)算法优化粒子滤波算法

粒子滤波算法虽然在理论上可以表示任意形式的概率分布，但是依然存在一系列的问题[16]，上文中的三个状态空间的参数ak,bk,ck在算法预测前就需要确定其初始值，现有的文献中确定这个初始值时虽然可以利用粒子滤波的状态跟踪能力通过观察数据跟踪获得，但获得的最优参数只是一个范围，具体值的确定依然需要依靠经验。本文提出使用粒子群(PSO)算法找出这三个参数的最优值，达到优化粒子滤波算法的预测能力的目的。

PSO可以描述为：对d维空间中随机初始化的一个粒子群的速度和位置进行迭代，每次迭代之后，计算其自身搜索到的历史最优解pbest和全部粒子的历史最优解gbest，并由适应度函数对每个粒子进行优化评价。迭代过程中每个粒子的速度和位置公式为

v=wi×vp+c1×r1×(pbest-x)+c2×r2×(gbest-x)

(10)

x=x+vp

(11)

式中：wi为惯性权重，本文取为0.7[17]；c1为粒子自身路径中的历史最值权重，一般取2；c2为群体最优值权重，一般取2；r1,r2为[0,1]内随机数。

本文中的适应度函数为

(12)

式中：y为观测值；yp为预测值；在经过300次迭代之后，粒子群算法停止优化。具体的优化过程如表1所示。

表1 PSO优化粒子滤波算法

2 转台精度衰退预测实现过程

转台精度衰退预测的具体实现过程如下：

(1) 信号降噪与重构，使用EEMD-PCA方法对原始数据降噪并进行信号重构[18]，通过使用聚合经验模态法(EEMD)将原始振动信号分解为若干组IMF(Intrinsic Mode Function)分量，再对这些组的IMF分量进行PCA，从而筛选出其中包含低频有效信息的IMF，再对筛选过的IMF分量重构成矩阵Ej，从而得到反映进度衰退的特征信号，同时起到降噪的目的。

(2) 选择统计特征量，组成特征观察值矩阵。通过Baum-Welch算法在已知的观察序列的基础上建立最有可能的HMM模型。本文通过观察序列OB10建立一个HMM模型λ10，代入测试数据计算得到精度衰退的对数似然概率曲线并诊断是否发生衰退，在此基础上建立健康状态指标H。本文选择了峭度(KU)、偏度(SK)、裕度指标(CL)、峰值指标(CF)、脉冲指标(IM)和波形指标(SI)等六个统计特征量。

由这些统计特征量组成的观察值矩阵为

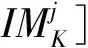
(13)

式中：OBj=[OBj1,OBj2, …,OBjK]的j对应下文的第j组数据。

定义描述转台精度衰退的健康状态指标为

H=P(OBj|λ10)

(14)

式中：λ10为用健康状态下的观察值矩阵OB10训练的HMM模型。

(3) 粒子滤波算法预测精度趋势。在经过粒子群算法优化得到最优的起始点参数ak,bk,ck的值后，使用粒子滤波算法对精度衰退趋势和剩余寿命进行预测，如表2所示。

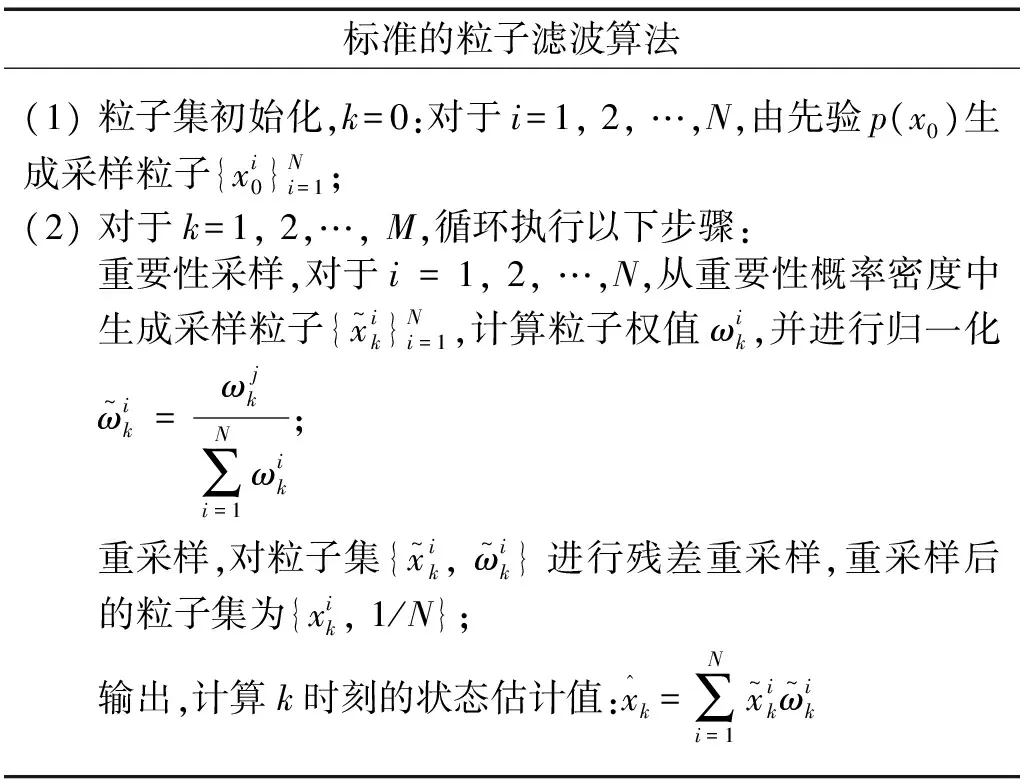
表2 标准粒子滤波算法

其中，

(15)

训练的粒子数定为2 000，σ1，σ2，σ3，σ4分别为8，0.007, 0.005，9。粒子滤波算法根据状态空间模型对精度状态进行迭代更新，输出每一步的状态估计值，在达到精度的阈值之后，根据精度的PDF分布以及预测失效点的位置计算数控转台的精度剩余寿命(Remaining Useful Life, RUL)。

转台精度衰退评估和剩余寿命计算的模型方案如图1所示。

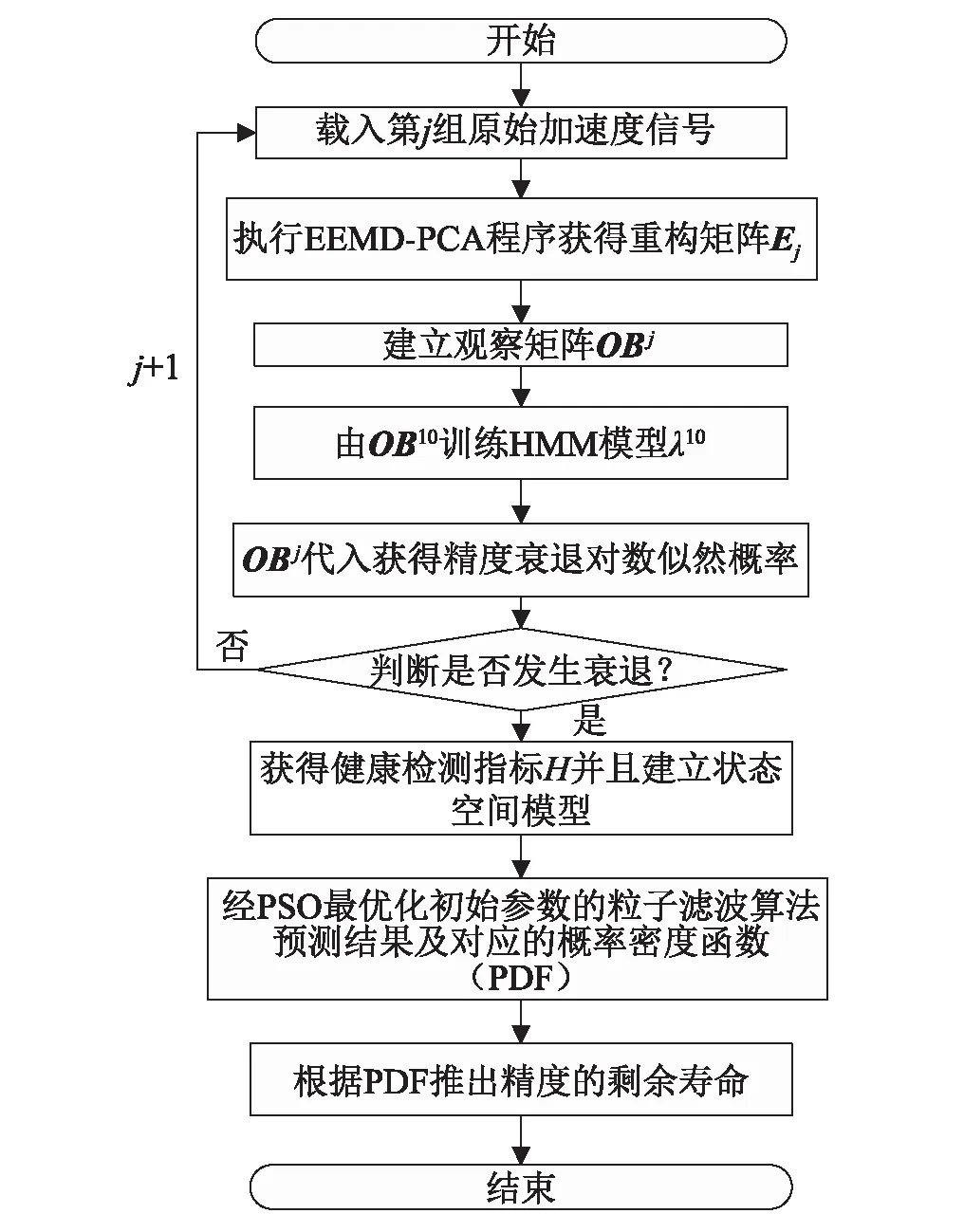
图1 数控转台精度衰退模型方案Fig.1 Model of precision decline of NC rotary table

3 数控转台精度衰退加速寿命试验

3.1 试验设备简介

本次的试验对象为国内某机床附件公司生产的TK13250E型数控立卧转台。工作台最高转速为11.1 r/min，定位精度为30"，重复定位精度为8"(调整前)，经间隙补偿后重复定位精度可达6"。如图2(a)所示，该数控转台由西门子s7-200 224XP型PLC控制的步进电机驱动，该PLC(Programmable Logic Controller)同时控制一个加载液压缸，振动加速度信号由PXI数据采集箱采集。加速度传感器1安装在蜗杆的轴线延长线位置上，加速度传感器2安装在电机传动齿轮的链接法兰上。由于蜗轮副的状态变化对转台的定位精度具有显著影响，所以本文中利用加速度传感器1采集的精度衰退全寿命信号进行分析。本次试验为转台的变载荷加速寿命试验，在试验的前200 h以100%的载荷运行转台，后520 h以200%载荷运行转台，采样频率为2 048 Hz。将样本分成了87组，其中以第10组样本为训练样本，其余为测试样本，每组122 886个样本。

为了验证该模型的有效性，在实验中使用激光干涉仪定期测量了转台的定位精度。实验设备为雷尼绍XL-80激光干涉仪系统，该设备回转测量时分度精度为±5 μm/m，重复精度为1 μm/m。如图2(b)所示，使用激光干涉仪每60 h测一次共测得12组数据。每次测量时需要将转台平放在操作台上，安装测量仪器。试验时，数控转台以10°为步长，正反交替转两圈获得一次测量值，每次试验测三次并取平均值。整个试验系统的原理图如图2(c)所示。

图2 数控转台精度衰退加速寿命试验系统Fig.2 Accelerated life test system ofaccuracy decline of NC rotary table

3.2 试验结果分析

通过对比分析试验采集的87组原始数据，在第10组～第30组数据的振动幅值十分平稳，从第39组数据开始幅值出现较大的增加，并且出现规律性的变化，图3(a)中对第10组、第39组和第50组数据进行了对比，从中可以看出，振动信号的幅值在全寿命周期中跃升了三个数量级。

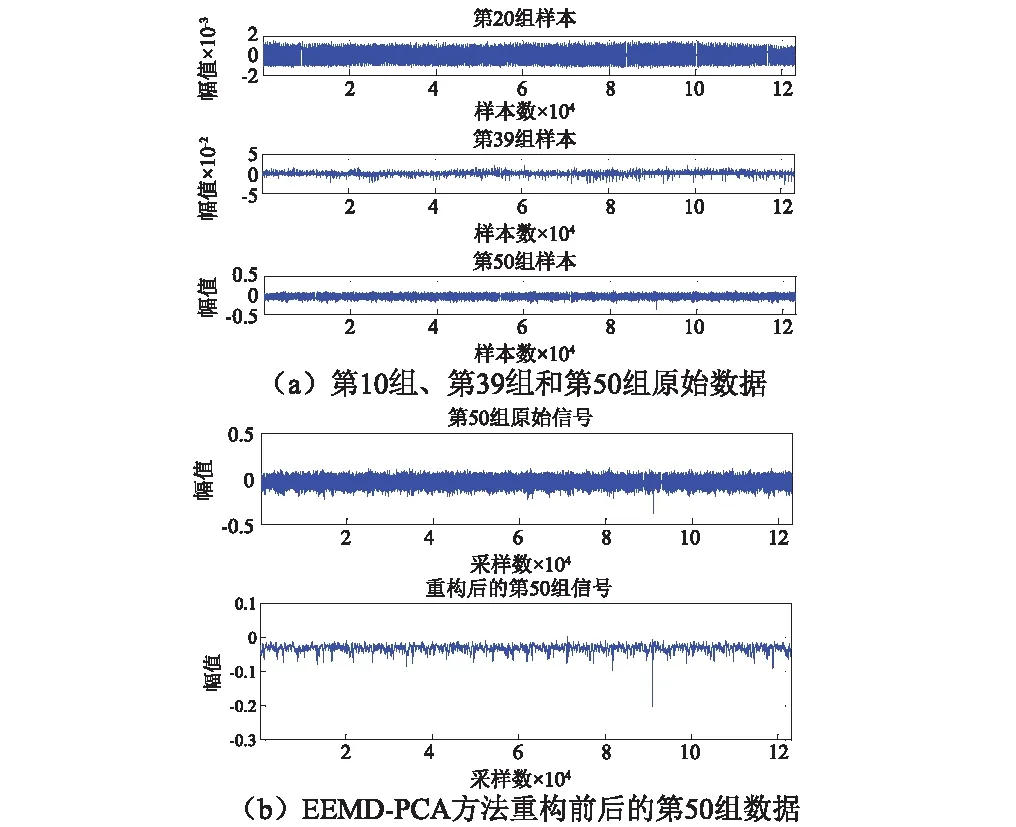
图3 第10组、第39组和第50组原始数据以及EEMD-PCA方法重构前后的第50组数据Fig.3 Raw data at file number 10、39 and 50 and Fiftieth sets of data before and after reconstruction by EEMD-PCA

获取了数据后使用EEMD-PCA方法对原始数据降噪并进行信号重构，图3(b)中以第50组数据为例，给出了重构前后的数据。从中可以看出，信号降噪和重构之后出现了比较明显的能反映精度变化的特征。同时，图4给出了表2中的统计特征量在代入重构信号时的计算结果，这些特征量对转台精度衰退的变化比较敏感，验证了表2的合理性。

将测试样本输入到经过第10组数据训练的HMM模型中，计算出一组对数似然概率值，该值反映了测试样本与训练样本的匹配度，如图5所示。选用第10组数据作为训练样本主要是考虑到转台在运转初期有一个磨合的过程，其初期的精度不是转台运转的最佳状态，经过对比前后的数据，认为第10组数据可以代表正常精度状态下的振动信号，并且由于本次试验的采样频率较高，所以一组数据的信息量足够大。

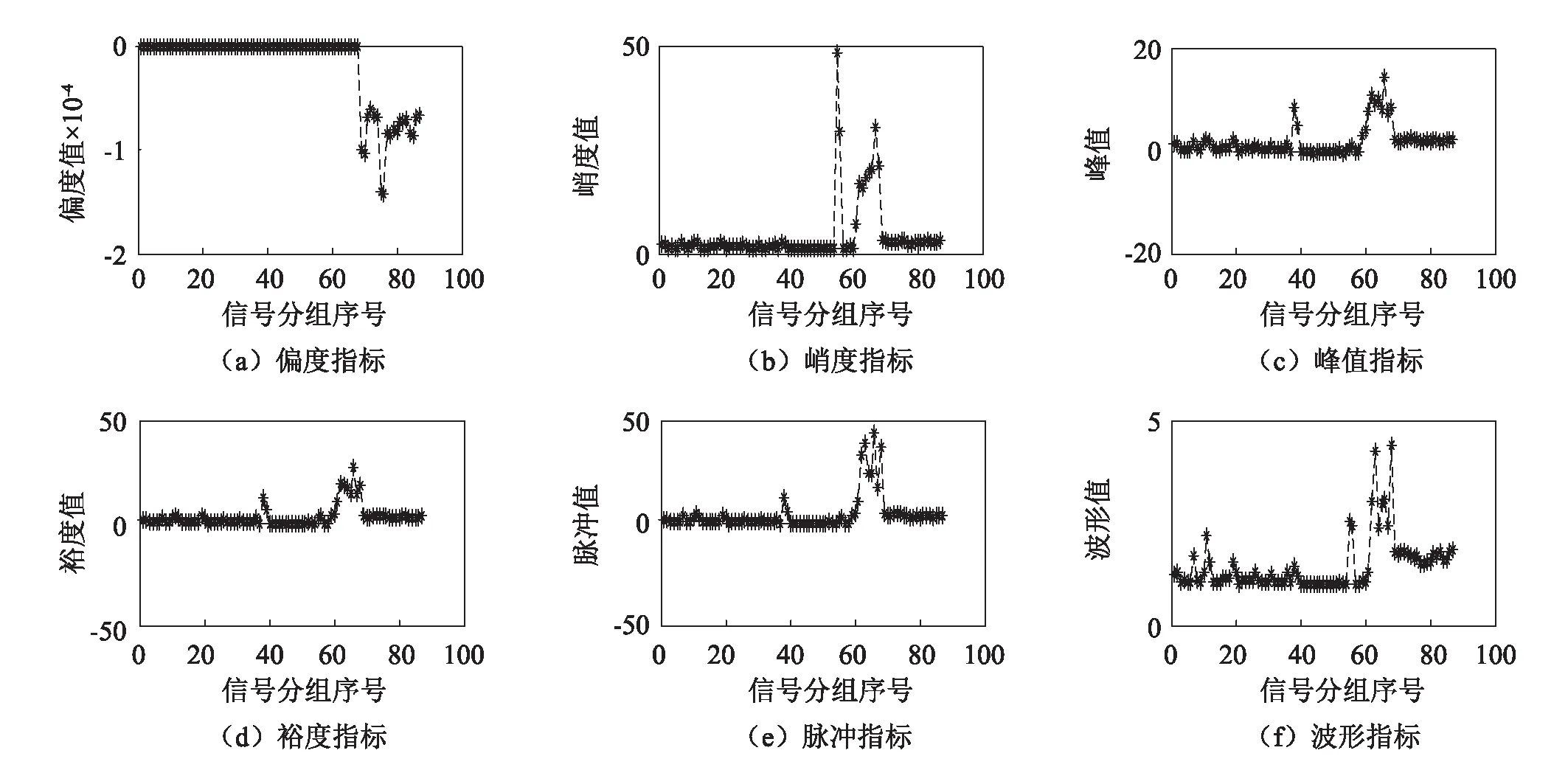
图4 统计特征量计算结果Fig.4 Calculation results of statistical characteristic quantities

从图中可以看出，在第39组数据时，匹配度有一个比较大的下降，可以判断转台精度从此时开始逐渐下降，本文将从第39组开始计算出的概率值作为健康状态指标H。同时对比图5和图6，可以看出在用激光干涉仪测量结果中第8次测量与第9次测量之间，转台的精度超过了设计允许的误差精度值8"，时间是在第480 h～第540 h，对应HMM计算的似然函数是在第67组，因此可以认为函数值在-100为精度失效的阈值。

这里需要说明的是，图6是利用激光干涉仪在数控转台精度衰退全寿命试验中测量得到的，它反映了整个精度衰退的过程的全貌，而在转台实际运转工作过程中，利用激光干涉仪获得的仅仅是某一个或几个点的精度值，它难以获得对整个运转周期完整的描述，只能判断是否精度失效，而无法反映出转台当前的精度状态。本文提出的算法模型通过对转台实际运转过程中监测获得的历史数据进行分析，可以得到转台精度衰退的趋势，描绘出转台所处的精度状态，并且可以以某一个精度未失效的点为起始点，来预测转台精度的变化趋势，判断出精度的剩余寿命，由此判断是否要对转台进行必要的调整。

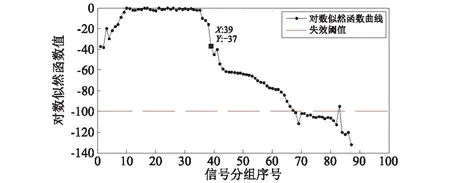
图5 数控转台精度衰退健康指标曲线Fig.5 Health indicators curve of accuracy decline of NC rotary table

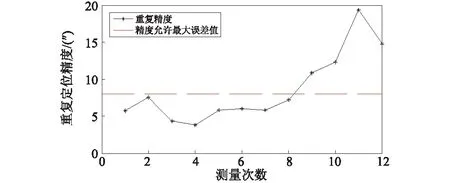
图6 激光干涉仪测量重复定位精度值Fig.6 Measurement accuracy of repeated positioning by laser interferometer

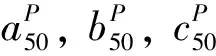
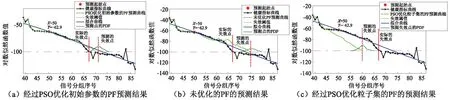
图7 三种算法预测结果图Fig.7 Prediction results of three algorithms

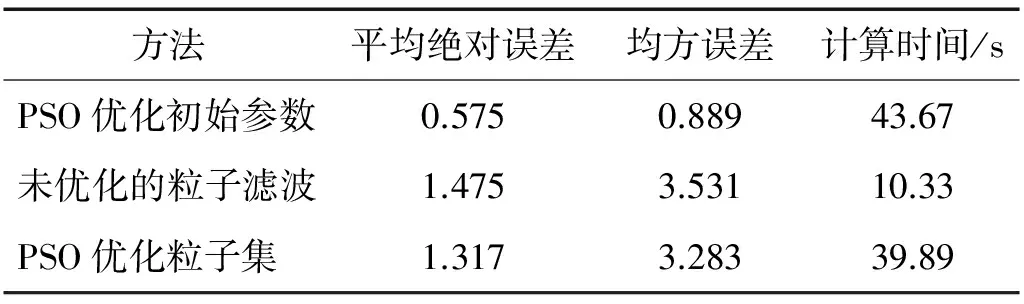
方法平均绝对误差均方误差计算时间/sPSO优化初始参数0．5750．88943．67未优化的粒子滤波1．4753．53110．33PSO优化粒子集1．3173．28339．89

表4给出以不同信号分组作为预测起始点的情况下三种算法的预测结果。其中，从第50组数据开始预测时，结合图7可以看出，三种方法的不确定度为50%时的预测结果分别是71、75和60，则可得到其剩余寿命(RUL)分别为21、25和10。通过激光干涉仪测量精度变化获得的实际的精度剩余寿命为17，差值分别为4、8和7。综合对比不同预测起始点的预测结果后认为本文提出的方法更加接近实际的结果。图8给出了本文提出的优化粒子滤波初始参数的方法在不同预测起始点的情况下，预测结果的PDF的分布曲线，可以看出起始点越大其分布越集中，说明其不确定度在变小，与实际情况是一致的。

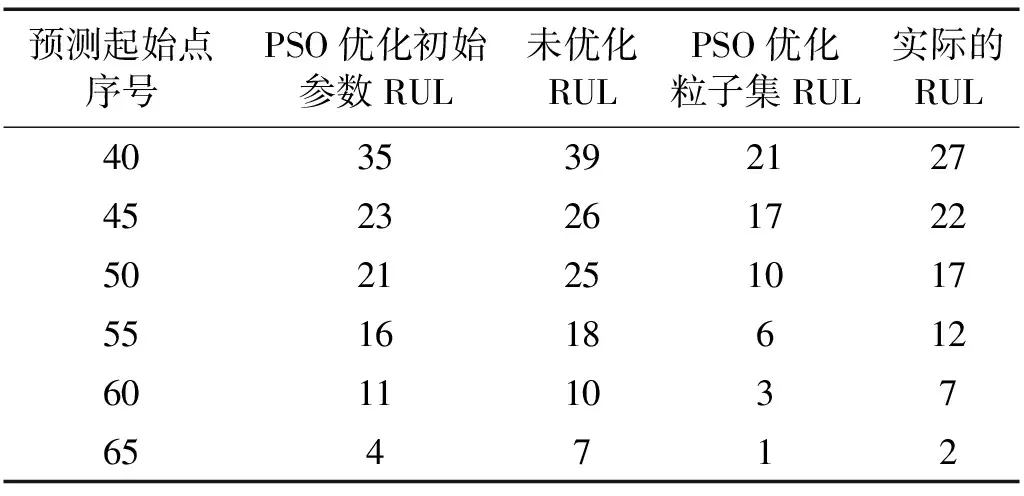
表4 不同起始点剩余寿命预测结果

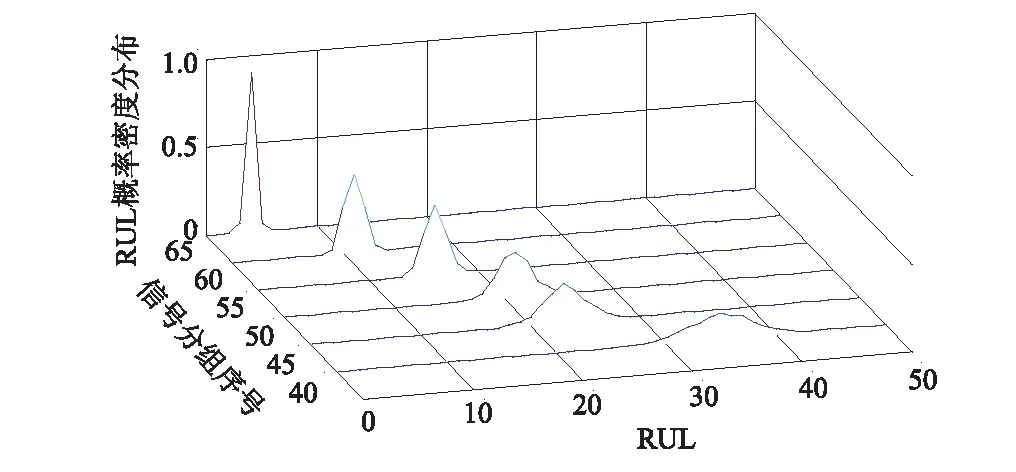
图8 PSO优化粒子滤波算法预测结果的PDF图Fig.8 PDF results of PF initial parameters optimizedby PSO

4 结 论

为了解决数控转台的精度衰退缺乏有效的描述方法且现有测量仪器只是测量工具而无法实现状态评估等问题。本文引入数据驱动的方法，提出数控转台重复定位精度衰退趋势预测模型，并得出如下的结论：

(1)本文区别于以往的状态识别，将HMM算法以新的角度运用于数控转台的精度衰退的研究中，结合优化后的粒子滤波算法，建立了一种预测转台精度衰退趋势的模型。在以第50组为预测起始点时，预测剩余寿命为21，实际剩余寿命为17，相差4，说明预测结果准确度较高。

(2)在使用粒子滤波算法的过程中，对粒子滤波算法的预测点初始参数使用PSO算法进行了优化，找出了最优的结果，并与未优化的粒子滤波算法以及用PSO优化粒子滤波粒子集方法的结果进行了对比分析，结果表明，虽然PSO优化初始参数的程序计算过程需要更长的时间，但是以第50组为预测起始点时，其预测结果与实际结果最接近，相差4，其他两种方法分别相差8和7。其他预测起始点时也是相同的情况。

[ 1 ] YU C J, HUANG X D, FANG C G, et al. Research on damping and vibration characteristic of the large and precision NC rotary table[J]. Advanced Materials Research, 2010, 97/98/99/100/101: 1216-1222.

[ 2 ] ŽVOKELJ M, ZUPAN S, PREBIL I. Non-linear multivariate and multiscale monitoring and signal denoising strategy using kernel principal component analysis combined with ensemble empirical mode decomposition method [J]. Mechanical Systems & Signal Processing, 2011, 25(7): 2631-2653.

[ 3 ] YU C J, HUANG X D, FANG C G. Research on dynamic characteristics of NC rotary table considering leakage factors of its hydrostatic guideway[J]. Journal of Mechanical Engineering Science, 2012, 226(11): 2674-2685.

[ 4 ] HENG A, ZHANG S, TAN A C C, et al. Rotating machinery prognostics: state of the art, challenges and opportunities [J]. Mechanical Systems & Signal Processing, 2009, 23(3): 724-739.

[ 5 ] BENKEDJOUH T, MEDJAHER K, ZERHOUNI N. Remaining useful life estimation based on nonlinear feature reduction and support vector regression [J]. Engineering Applications of Artificial Intelligence, 2013, 26(7): 1751-1760.

[ 6 ] LU C, CHEN J, HONG R, et al. Degradation trend estimation of slewing bearing based on LSSVM model [J]. Mechanical Systems & Signal Processing, 2016, 76/77:

353-366.

[ 7 ] MATEJ Z, SAMO Z, IVAN P. Non-linear multivariate and multiscale monitoring and signal denoising strategy using kernel principal component analysis combined with ensemble empirical mode decomposition method[J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2631-2653.

[ 8 ] FENG Y, HUANG X, HONG R, et al. Residual useful life prediction of large-size low-speed slewing bearings-a data driven method[J]. Journal of Vibroengineering, 2015, 17(8): 4164-4179.

[ 9 ] 于春健.多物理场耦合的大重型数控回转工作台动静态精度研究[D]. 南京：南京工业大学，2012.

[10] WANG D, MIAO Q, ZHOU Q, et al. An intelligent prognostic system for gear performance degradation assessment and remaining useful life estimation [J]. Journal of Vibration & Acoustics, 2015, 137(2): 12.

[11] 张西宁, 雷威, 李兵. 主分量分析和隐马尔科夫模型结合的轴承监测诊断方法[J]. 西安交通大学学报,2017, 51(6): 1-7.

ZHANG Xining, LEI Wei, LI Bing. Bearing fault detection and diagnosis method based on principal component analysis and hidden markov model [J].Journal of Xi’an Jiaotong University, 2017, 51(6)： 1-7.

[12] 余龙华,王宏,钟洪声. 基于隐马尔科夫模型的人脸识别[J]. 计算机技术与发展,2012, 22(2): 25-28.

YU Longhua，WANG Hong，ZHONG Hongsheng. Face recognition based on hidden markov model [J].Computer Technology and Development, 2012, 22(2): 25-28.

[13] RABINER L R. A tutorial on hidden Markov models and selected applications in speech recognition [J]. Readings in Speech Recognition, 1990, 77(2): 267-296.

[14] ARULAMPALAM M S, MASKELL S, GORDON N. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174-188.

[15] 王法胜, 鲁明羽, 赵清杰, 等. 粒子滤波算法[J]. 计算机学报,2014,37(8): 1679-1694.

WANG Fasheng, LU Mingyu, ZHAO Qingjie, et al. Particle filtering algorithm [J]. Chinese Journal of Computer, 2014, 37(8): 1679-1694.

[16] 方正, 佟国峰, 徐心和. 粒子群优化粒子滤波方法[J]. 控制与决策,2007, 22(3): 273-277.

FANG Zheng, TONG Guofeng, XU Xinhe. Particle swarm optimized particle filter [J].Control and Decision, 2007, 22(3): 273-277.

[17] 王维博, 林川, 郑永康. 粒子群算法中参数的实验与分析[J]. 西华大学学报(自然科学版),2008, 27(1): 76-80.

WANG Weibo, LIN Chuan, ZHENG Yongkang. Experiment and analysis of parameters in particle swarm optimization [J]. Journal of Xi Hua University (Natural Science), 2008, 27(1): 76-80.

[18] 封杨, 黄筱调, 陈捷, 等. 大型回转支承非平稳振动信号的EEMD-PCA降噪方法[J]. 南京工业大学学报(自然科学版), 2015, 37(3): 61-66.

FENG Yang, HUANG Xiaodiao, CHEN Jie, et al. EEMD-PCA based denosing method for non-stationary vibration signals of large-size slewing bearings [J].Journal of Nanjing Tech University(Natural Science) ,2015, 37(3):61-66.