驱动轮齿焊接径向变形的优化与预测

赵永满，付 威，侯晓晓，胡 斌

(1.石河子大学 机械电气工程学院，新疆 石河子 832000；2.黄河交通学院 汽车工程系，郑州 450062)

0 引言

驱动轮齿是覆土滚筒实现转动和覆土的关键零件，工作时，驱动轮齿与铺膜地面接触，轮齿径向长度影响地膜破坏率和种孔错位率[1-2]。生产时，12个驱动轮齿通过焊接均匀分布在薄壁环形件表面，易产生径向变形，影响轮齿径向尺寸精度[2]。因此，有效优化和预测驱动轮齿焊接径向变形，成为降低地膜破坏率和种孔错位率的重要工作。

焊接数值模拟因不受物理条件制约、成本较低等优点受到学者热衷，被验证可靠有效[3-4]。焊接速度和焊接顺序是影响焊接变形的两个重要因素[4-5]。为此，本文以焊接速度和焊接顺序为因子，驱动轮齿径向变形为试验指标，设计两因素三水平正交试验。借助Sysweld软件模拟试验方案，对结果进行方差分析，以优化试验参数[6]；同时，预估计最优方案下响应值上限。采用Minitab软件建立焊接参数(焊接速度、焊接顺序)与预测响应值(驱动轮齿径向变形)的定量关系，实现焊接变形预测与控制，并通过现场试验进行了验证。

1 外缘圈和驱动轮齿焊接结构

焊接方式采用手工电弧焊，焊接电流200A、焊接电压24V、焊丝牌号JQ-MG50-6(直径16mm，长40mm)、保护气体为CO2(气体流量15～20L/min)。焊件包含外缘圈(内径427mm，宽25mm，壁厚4mm，材料Q235)和驱动轮齿(直径φ16mm，长45mm，材料Q235)，12个驱动轮齿通过焊接均匀分布在外缘圈外表面，如图1所示[7-8]。

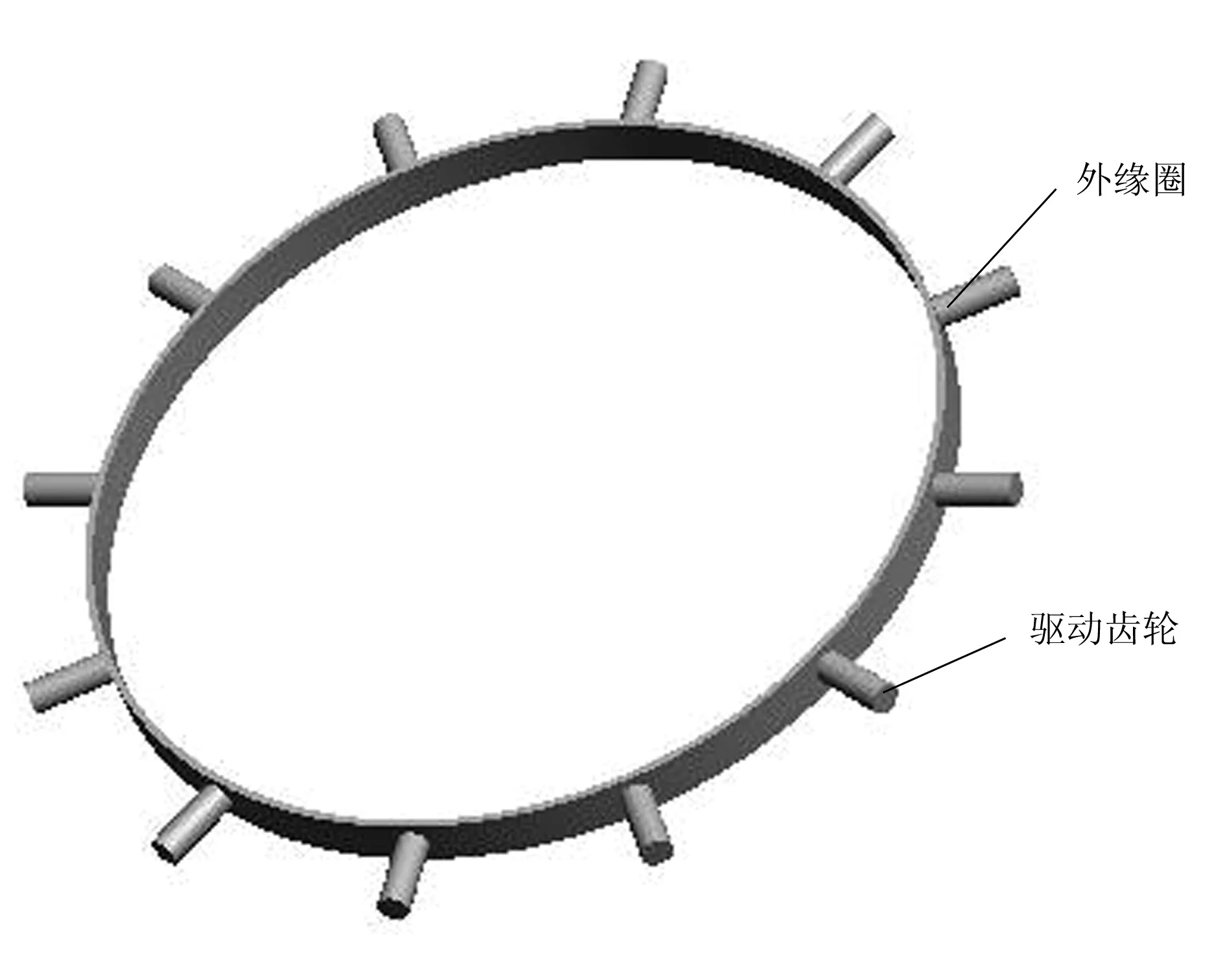
图1 外缘圈和驱动轮齿结构Fig.1 Outer circle and drive gear teeth struc

2 试验方法

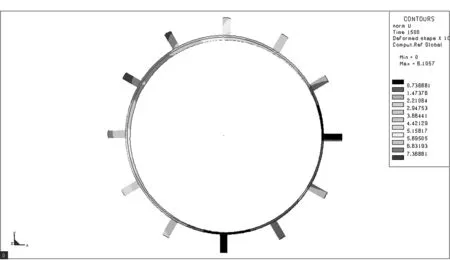
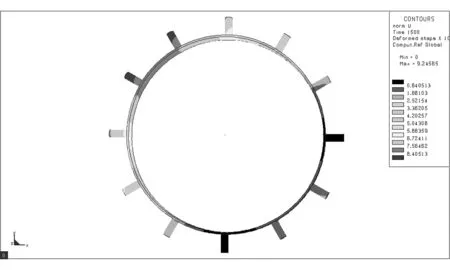
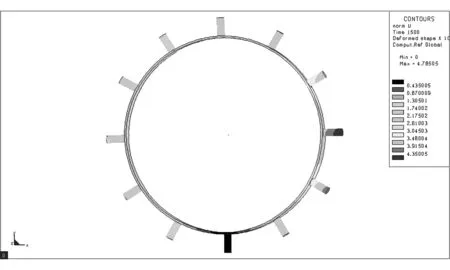
采用L9(34)正交表设计试验方案，借助Sysweld软件对各试验号进行数值模拟，获取分析结果[9]。Sysweld软件部分模拟结果如图2所示。对模拟结果进行方差分析，确定最优组合参数，估计最优组合下驱动轮齿径向变形上限。采用多元二次回归方程拟合焊接速度、焊接顺序与驱动轮齿径向变形的数学模型，预测不同焊接速度和焊接顺序时的变形。试验因素与水平设计如表1所示。其中，现场焊接速度为3.85mm/s，焊接顺序为间断跳焊II。试验方案及结果如表2所示。

(a)

(b)

(c)

(d)

(e)

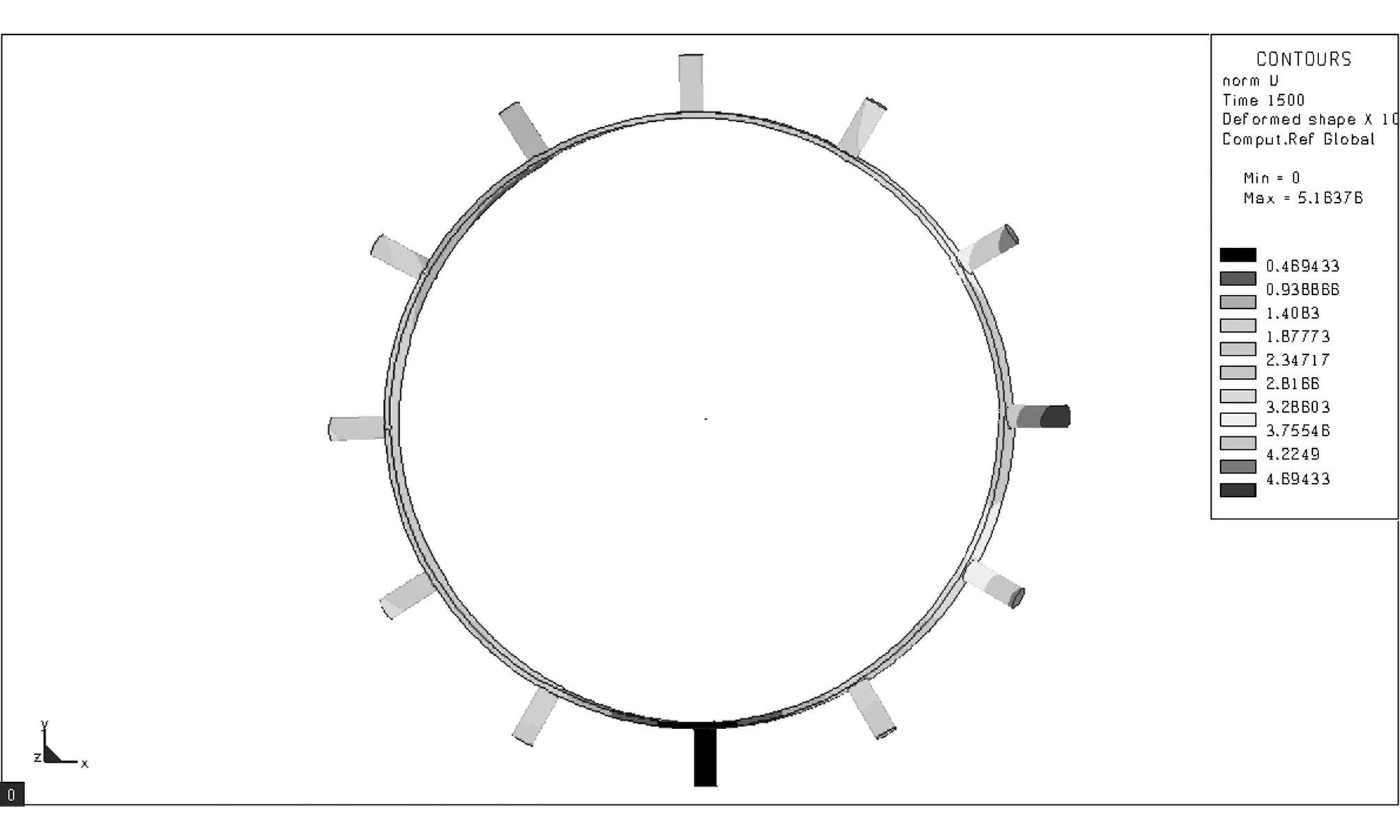
(f)

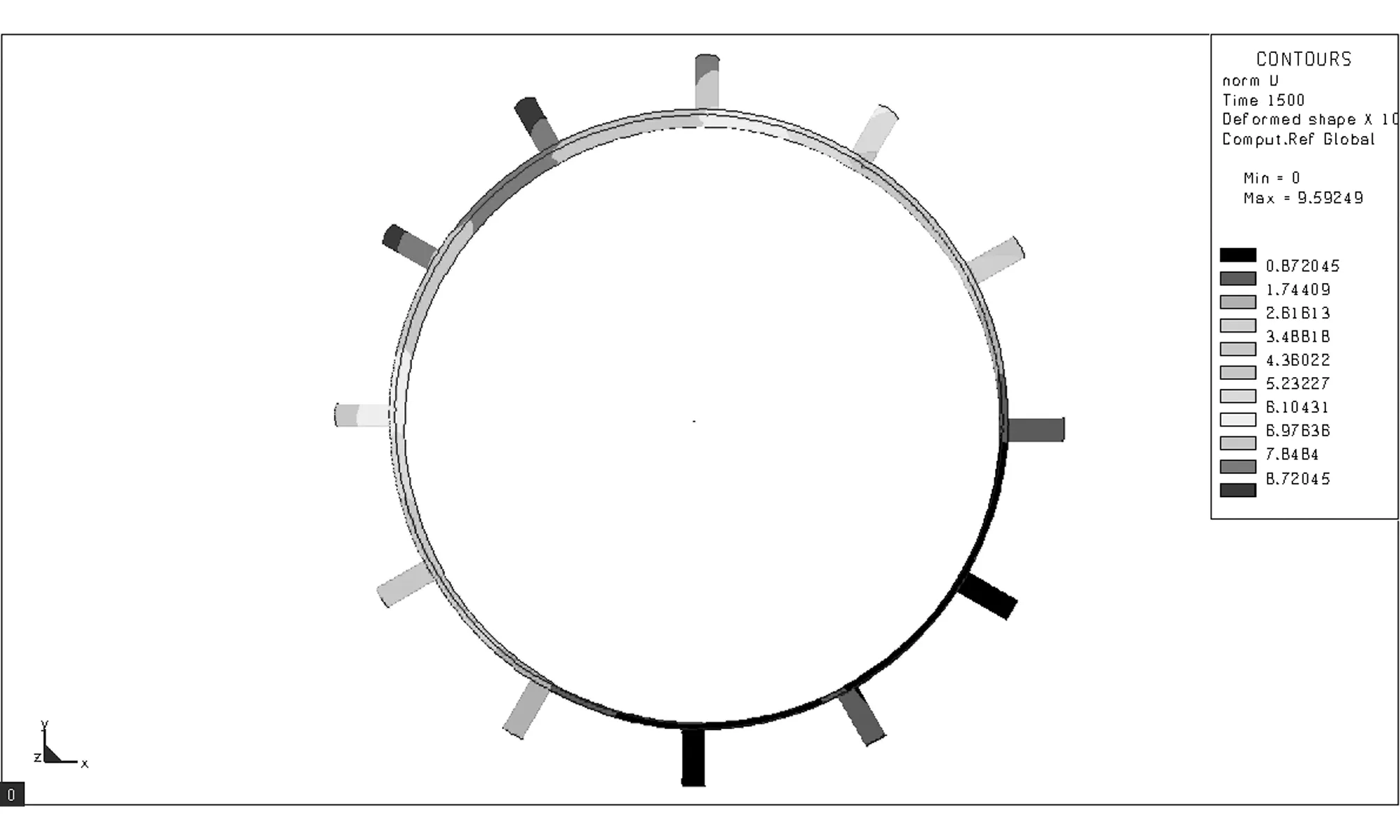
(g)

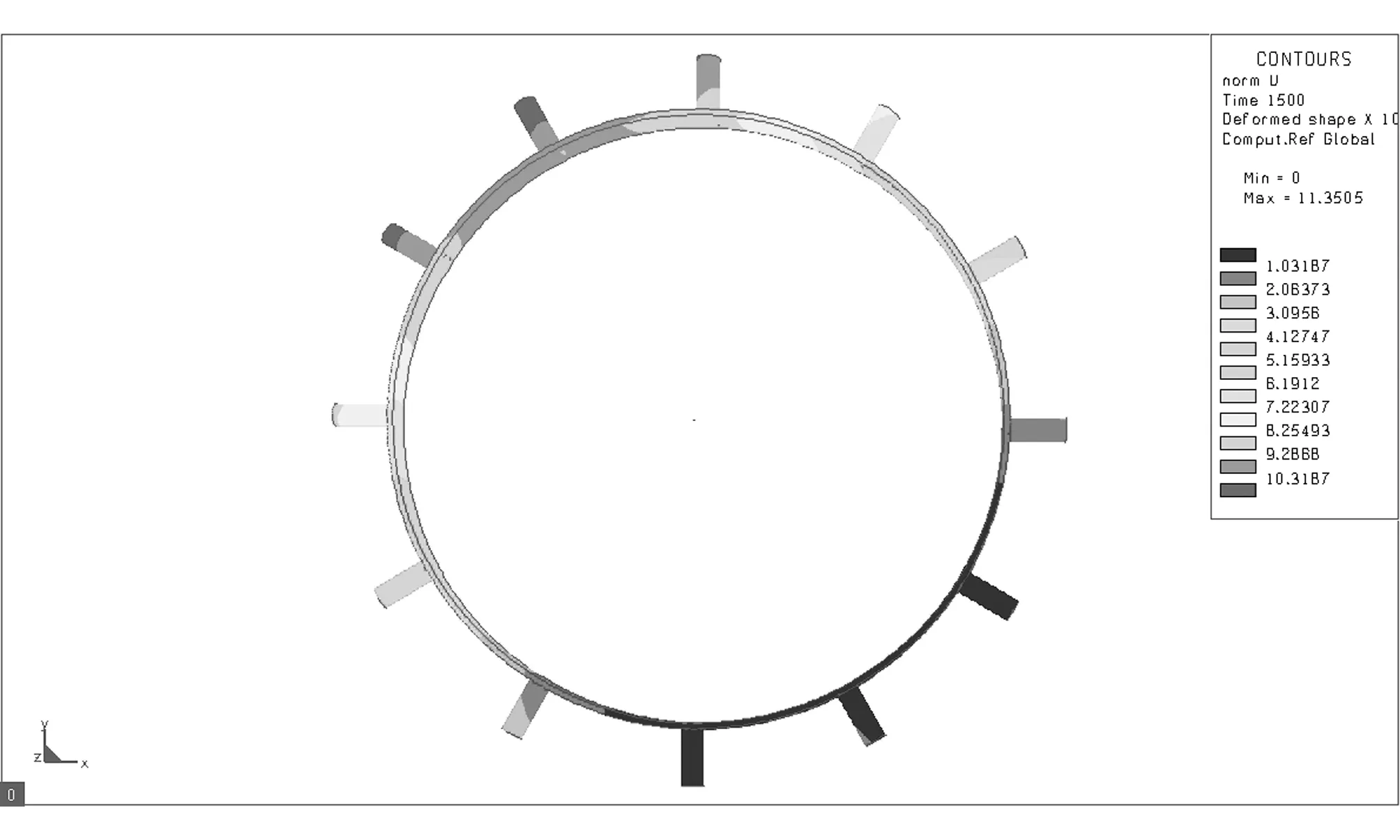
(h) 图2 数值模拟结果Fig.2 Result of numerical simulation表1 焊接模拟因素水平表 Table 1 Factors and levels for welding simulation

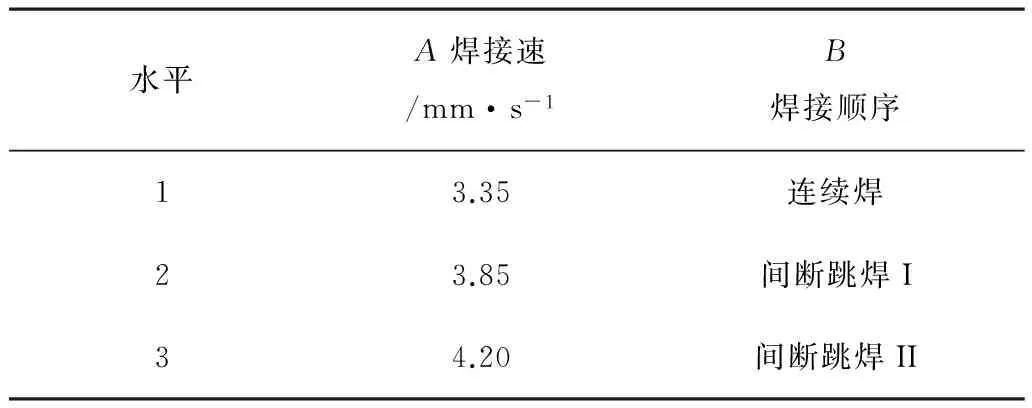
水平A焊接速/mm·s-1B焊接顺序13.35连续焊23.85间断跳焊I34.20间断跳焊II

3种焊接顺序分别见图3中的(a)、(b)、(c)。

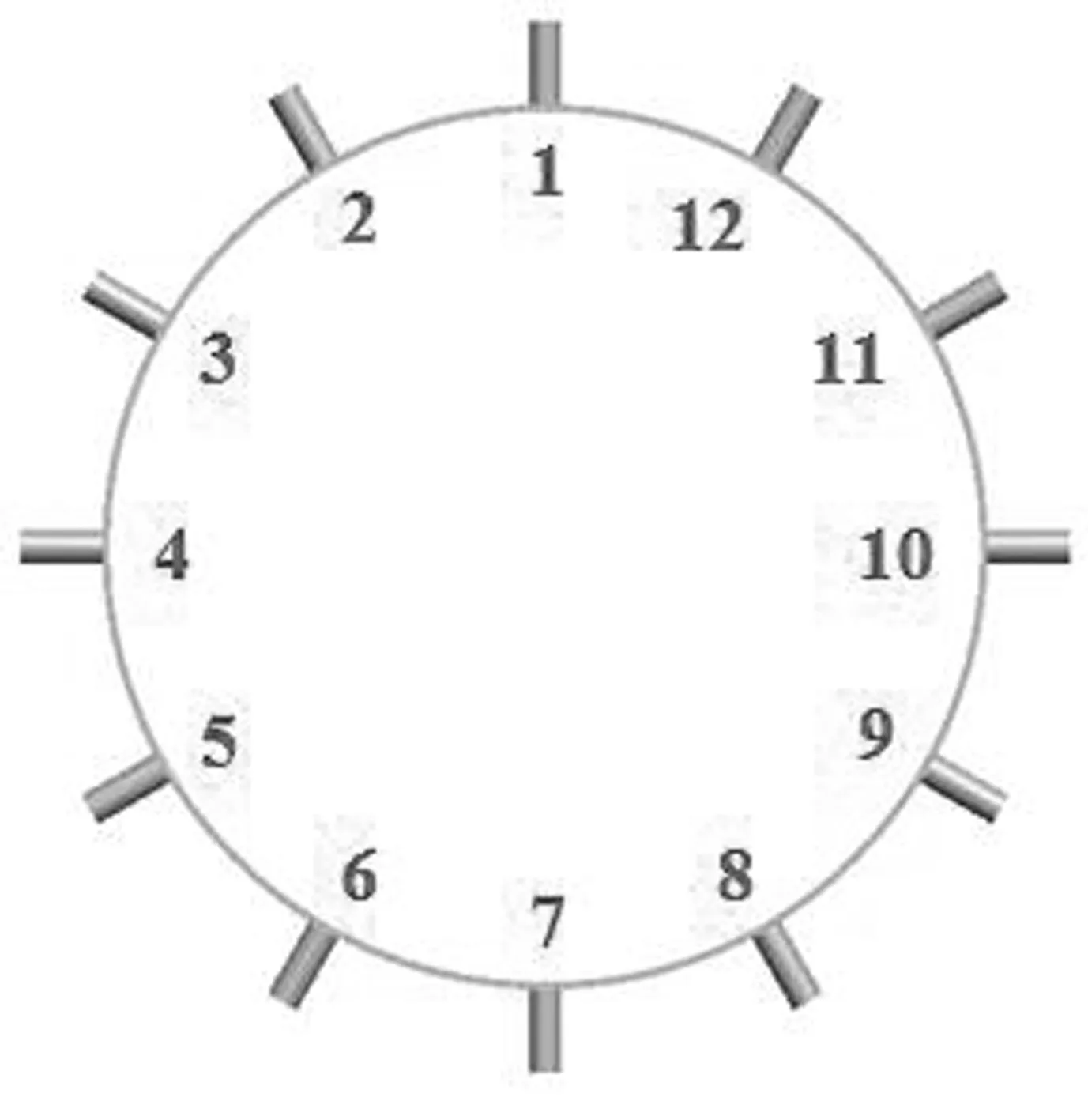
(a)连续焊

(b)间断跳焊I

(c)间断跳焊II 图3 外缘圈和驱动轮齿焊接顺序

3 试验结果与分析

3.1 参数优化

对模拟结果进行方差分析，计算过程如表2所示。

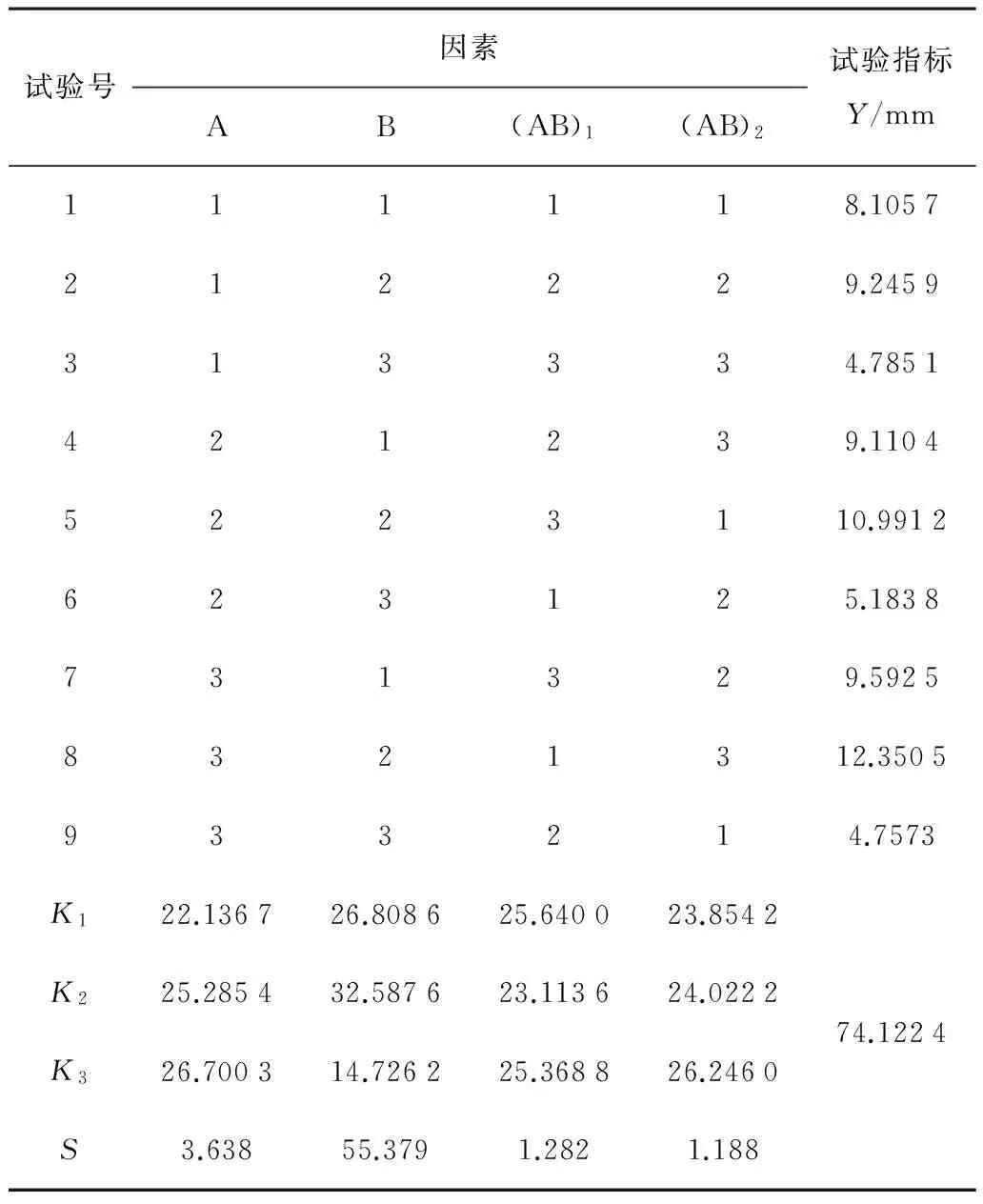
表2 试验结果及计算Table 2 Test results and calculations

方差分析如表3所示。由表2可知：交互作用AB的离差平方和S值很小，可作为误差项。驱动轮齿的变形越小越好，根据表2中各因素K值的最小值确定优水平，即A1B3。由表3可知：在95%置信度下，因素B(焊接顺序)对径向变形影响极显著，因素A(焊接速度)有一定影响。因此，水平组合为A1B3。

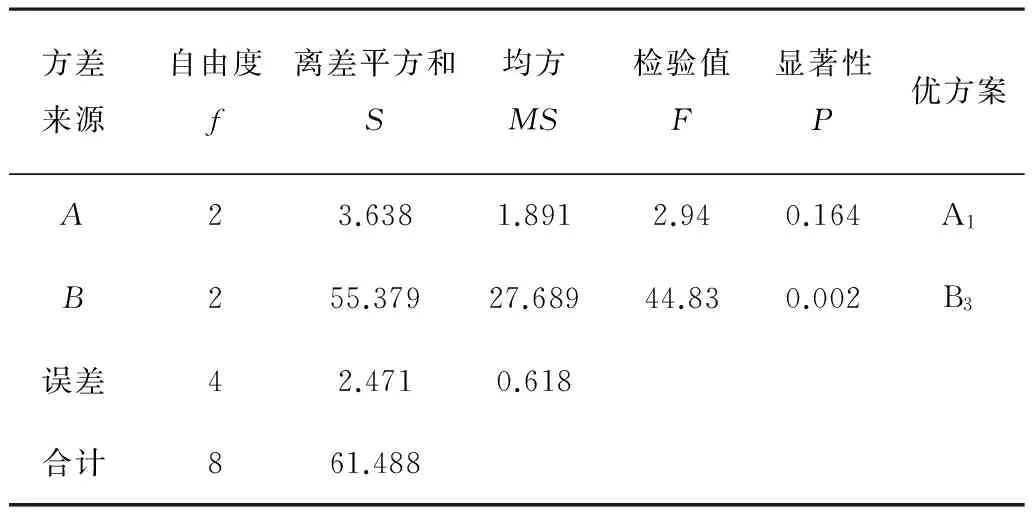
表3 方差分析表Table 3 Variance analysis of K

S=0.785 925，R-Sq=95.98%，R-Sq(调整)=91.96%。

3.2 最优组合下响应值上限估计

由方差分析和回归方程确定的最优方案A1B3下变形为定值。但实际生产中，焊接干扰因素多样且复杂，响应值产生一定浮动，有必要估计最优方案下响应值上限μ上。

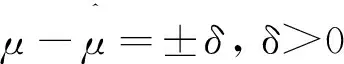
(1)

所以

(2)

(3)

所以

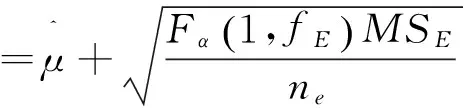
B为显著因素，将因素A的离差平方和并入误差，则新的误差平方和SE、新的误差自由度fE、nE分别为

SE'=SE+SA=6.109，fE'=fE+fA=6，ne=3

所以

在95%置信度下，F0.05(1，6)=5.99，则响应值上限为μ上=9.661 5，这表明生产中驱动轮齿径向变形量不会大于9.661 5mm。

3.3 预测模型

采用Minitab软件对模拟结果进行响应曲面回归分析，剔除不显著项。式(4)为以焊接速度和焊接顺序为变量的驱动轮齿径向变形的二元回归模型(使用未编码单位，焊接顺序B取1、2、3)，表4和表5分别为估计回归系数和方差分析[10-11]。

表4 Y的估计回归系数Table 4 Estimated regression coefficients of Y

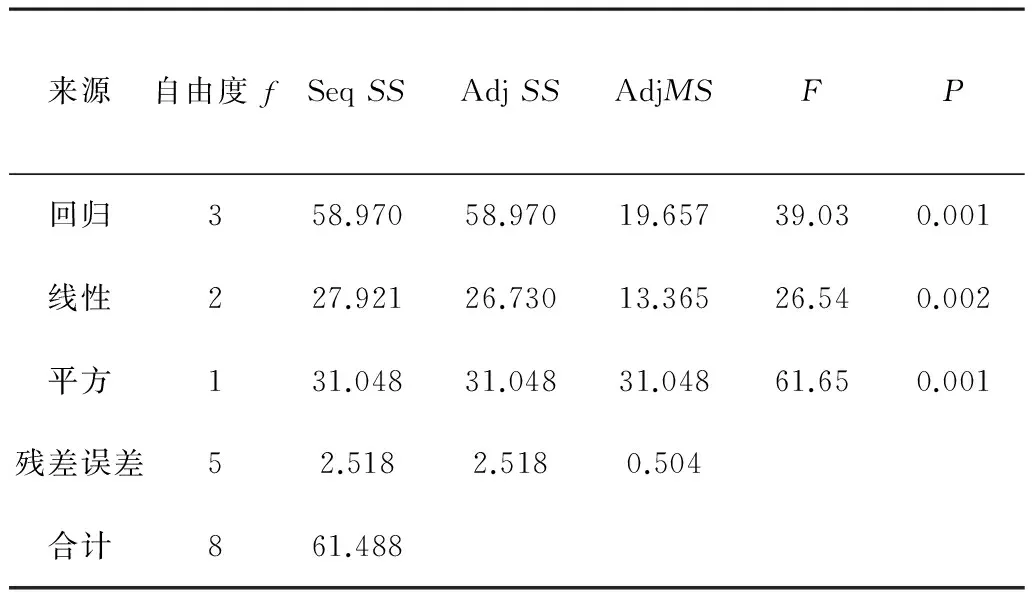
表5 Y的方差分析Table 5 The variance analysis of Y

分析表4：在95%置信度下，项B、B×B回归系数高度显著，A回归系数显著。R2=95.90%，调整R2=93.45%，表明曲面拟合得极好；预测R2(预测)=83.86%>80%，表明曲面方程能够较好预测响应值Y；而且预测R2与R2、调整R2值相差较小，表明响应曲面没有过度拟合。由表5可知：在95%的置信度下，回归方程、一次项、二次项均高度显著。综上，该响应曲面拟合良好，响应曲面回归方程为

Y=-7.751+1.811A+13.747B-3.940B×B

(4)

作等值线图和3D曲面图，如图4所示。

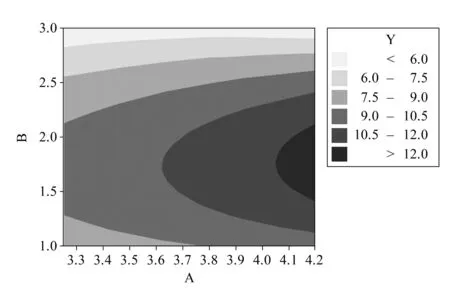
(a) 等值线图

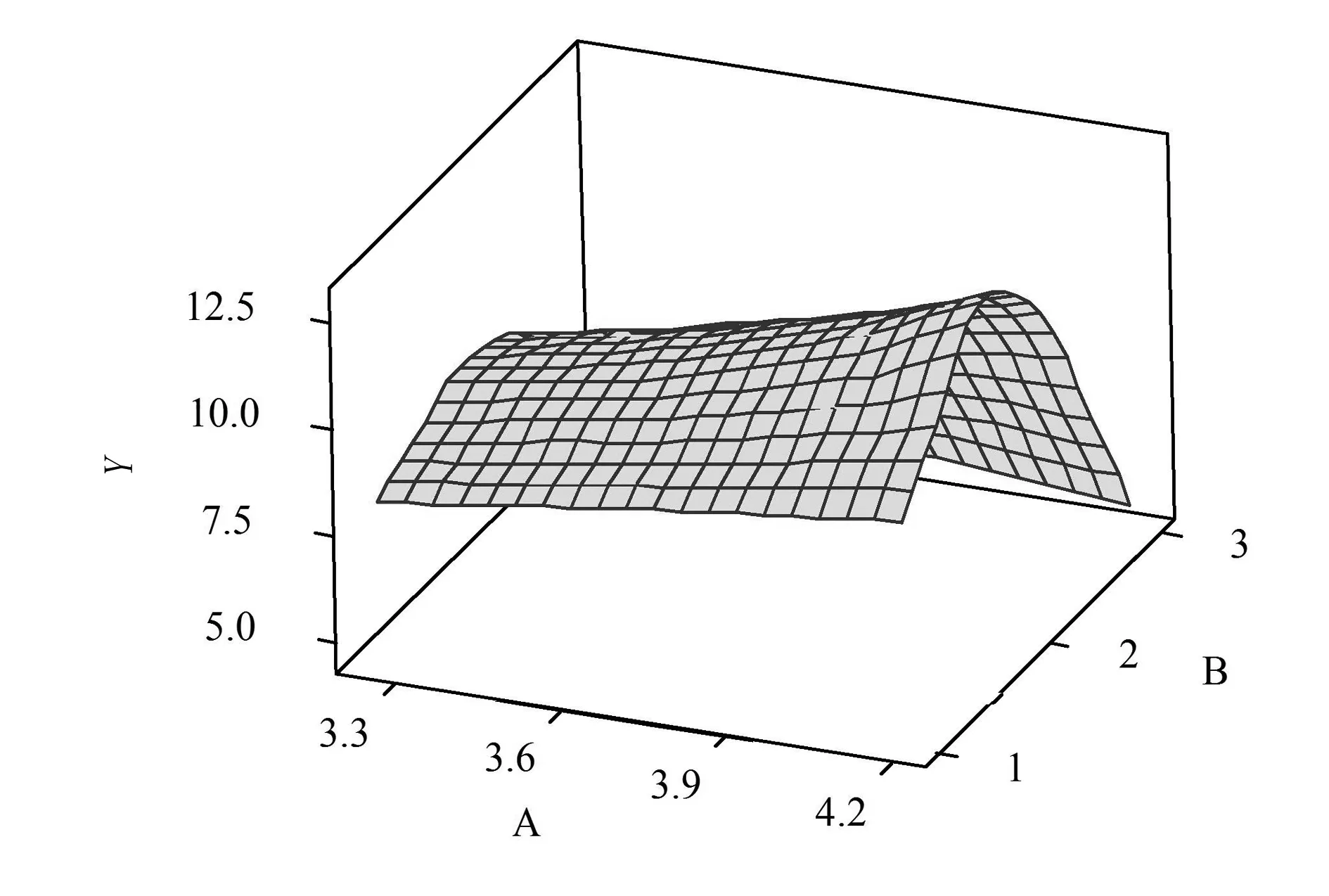
(b) 3D曲面图 图4 Y的等值线图和3D曲面图Fig.4 Contour map and surface plot of Y and B,A

分析等值线图，与A方向相比，Y在B方向数值变化程度较大，B为主要因素。当B取B3、A取A1时，Y值最小。由3D曲面图亦可得出该结论为焊接变形量Y的优搭配为A1B3，其与参数优化结果一致，可用来预测和控制焊接变形量Y。

3.4 试验验证

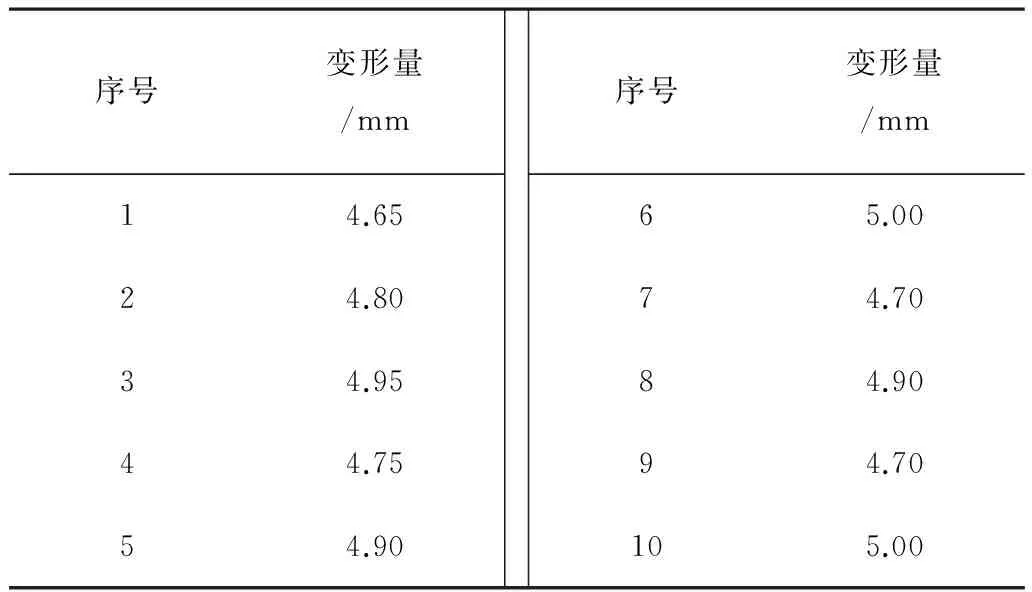
表6 优化前指标结果Table 6 Indicator results before optimizing

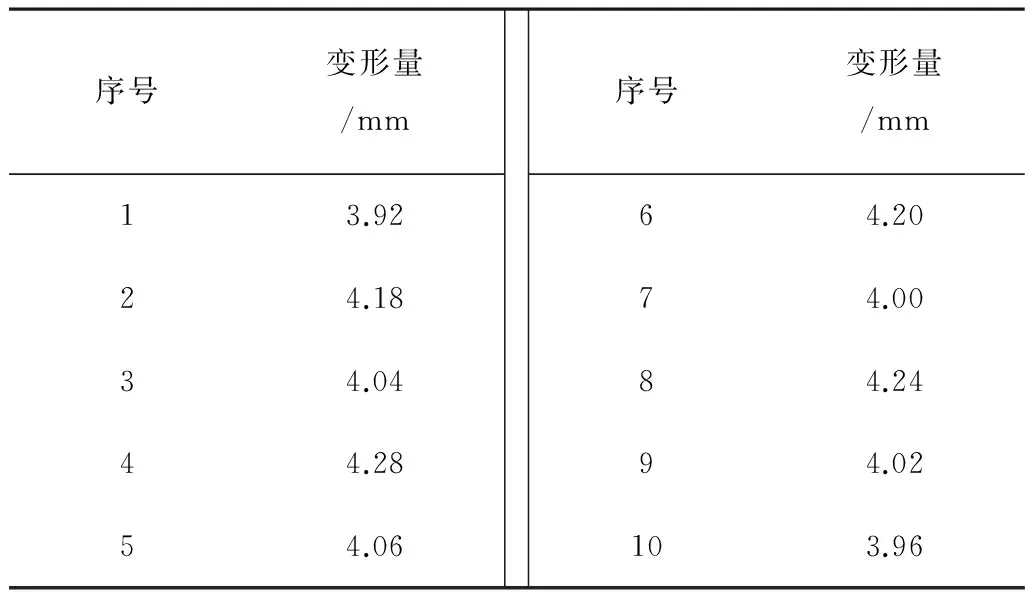
表7 优化后指标结果Table 7 Indicator results after optimizing

3.5 改进效果验证

为了消除随机误差，将焊接速度定为4.20mm/s，采用图3(c)中的焊接顺序对外缘圈和驱动轮齿进行焊接，并抽取25组覆土滚筒成品进行左右半轴的同轴度测量，每组包含4个子组。制定控制图，如图5所示。

由图5可知：图中每个同轴度样本值都处于控制线内，而且样本的上控制线低于分析用控制图(图3～图5)中的上控制线，表明经过过程改进后，覆土滚筒生产过程处于稳态，覆土滚筒左右半轴同轴度能够满足生产技术要求(低于500mm)。因此，将分析用控制图转化为控制用控制图以判断覆土滚筒后期生产过程稳定性。

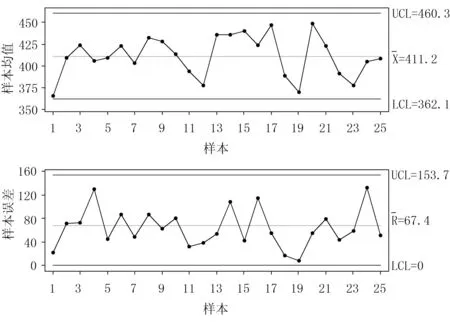
图5 控制用控制图Fig.5 The controlling control chart

4 结论

1)基于正交试验方案确定降低驱动轮齿焊接变形的最优组合参数：焊接速度4.20mm/s、焊接顺序间断跳焊Ⅱ，焊接顺序对变形影响高度显著。最优组合参数下变形量的估计上μ上=9.661 5mm。

2)基于响应曲面法建立驱动轮齿焊接变形与焊接速度和焊接顺序的多元二次回归数学模型显著性高，且拟合极好。

3)最优方案试验表明：平均变形量降低了18.22%，测量值均未超过估计上限；测量值和预测值的绝对误差小于5%，预测模型可靠。

[1] 陈学庚,赵岩.棉花双膜覆盖精量播种机的研制[J].农业工程学报，2010，26(4)：38-41.

[2] 董文超,陆善平,李殿中.焊接顺序对大型薄板装甲钢结构变形的影响[J].焊接学报，2015，36(7)：43-46.

[3] 郭广飞,王勇,韩涛.天然气管道在役焊接径向变形数值模拟[J].焊接学报，2014，35(12)：55-58.

[4] 李江飞,齐海波,任德亮,等.薄壁多焊缝复杂构件焊接过程的数值模拟[J].焊接学报，2015，36(1)：87-90.

[5] 张国栋,薛吉林,周昌玉.基于正交试验设计的高温管道焊接工艺优化[J].焊接学报，2008，29(11)：54-56.

[6] 吕小莲,胡志超,张会娟,等.气吸式花生膜上精量穴播轮田间作业性能测试[J].西北农林科技大学学报,2014,42(6):213-218.

[7] 李晓延,武传松,李午申.中国焊接制造领域学科发展研究[J].机械工程学报,2012,48(6)：19-31.

[8] 范玉滨,杨然兵,柴恒辉,等.膜上苗带覆土装置设计与实验研究[J].中国农机化学报,2014，32(5)：5-8.

[9] 朱宁帅,刘元义.基于遗传算法的叶轮的优化设计[J].中国农机化学报,2014，35(4)：107-110.

[10] 高国华,冯天翔,李福.斜入式穴盘苗移栽手抓工作参数优化及实验验证[J].农业机械学报,2015,31(24)：16-22.

[11] 丁素明,薛新宇,方金豹,等.手持式风送授粉机工作参数优化与实验[J].农业工程学报,2015,31(8)：68-75.

[12] 陈魁.试验设计与分析[M].北京:清华大学出版社，1996.