非对称因素对舰载机弹射起飞安全的影响

林佳铭，张轶，乐挺，王立新

（北京航空航天大学 航空科学与工程学院，北京 100083）

舰载机在弹射起飞过程中的运动变化剧烈，并且受到多种环境因素的耦合影响，因而具有较大的复杂性和危险性［1］。在实际的弹射作业条件下，一些非对称因素将对飞机弹射滑跑和离舰上升2个阶段的飞行特性造成影响：①定位偏心使飞机在弹射滑跑时出现偏航振荡运动［2-3］，并导致其在离舰上升时出现横航向运动偏离；②弹射道偏角使飞机在弹射滑跑时产生侧滑，进而改变其横航向运动状态；③甲板横摇使飞机在离舰时具有一定的滚转角，并影响其纵向爬升性能［4］。

针对舰载机弹射起飞安全性方面的问题，Lucas较早开展了相关研究，并提出相应的安全性评价准则［5］，这一准则在后续的研究中被广泛参考，应用于机舰参数适配规律研究［6］、复杂起飞环境因素的综合影响分析［7］、弹射起飞上升段的自动控制律设计［8］、F/A-18E/F的 海试验证［9］等。在上述的研究和试验中，主要研究飞机弹射后的纵向安全性要求，并未涉及其横航向运动以及相应的安全性要求。

近年来国内外的一些研究中开始关注非对称因素的影响。Sten研究了固定翼飞机与航母的适配评估需求［10］，指出应当考虑斜角甲板弹射、非对称装载配平及侧风的影响；Kelley就弹射时飞机的偏航运动特性进行了理论分析计算［11］；Small对XAJ-I和E-2A 2种机型开展了地面偏心弹射试验［12］，为研究舰载机的偏航运动特性和弹射杆的载荷波动提供了参考；朱齐丹等研究了定位偏心时，舰载机甲板滑跑段的弹射动力学过程及其对飞机姿态的影响［3］；于浩和聂宏则对弹射杆的载荷情况进行了建模仿真计算［13］。但是在目前国内外公开文献中，尚鲜见有对飞机离舰上升段的横航向运动偏离特性的分析，以及非对称因素对弹射起飞机舰适配性影响的研究等。

F/A-18E/F飞行手册［14］指出，在非对称装载情况下，期望飞机在弹射离舰后的3 s内滚转角应小于5°，故可以选取滚转角作为飞机横航向安全性的评价指标。此外，由于安全甲板风（Wind Over Deck，WOD）包线［15-16］能够反映飞机弹射起飞时对母舰甲板风风向和风速的要求，并且具有简洁直观的特点，因此可以通过研究安全甲板风包线的变化情况，从而评价非对称因素对弹射起飞安全性的影响。

本文通过理论分析和建模仿真，研究了定位偏心、弹射道偏角和甲板横摇等非对称扰动因素对飞机弹射滑跑和离舰上升2个阶段运动特性的影响与规律。在此基础上，基于弹射起飞的安全性要求，计算确定了安全甲板风包线，分析其边界约束条件，以及非对称因素对甲板风包线的影响规律。研究结果可为舰载机非对称弹射特性的量化评估、安全甲板风包线的确定、弹射作业效率的优化提高等提供一定的理论参考。

1 弹射起飞的数学模型

采用多体动力学方法建立的弹射起飞仿真模型［17］，是分析计算航母、海面大气环境等因素对舰载机弹射起飞特性影响的重要辅助工具。其中的起落架动力学模型［18］，可以准确地描述机舰之间的位置约束与作用力的传递关系。本文在研究舰载机非对称起飞问题时，首先建立了3轴耦合的飞机6自由度运动模型，并取北东地坐标系作为惯性参考系，分别以质心坐标位置［x，y，z］T和姿态角［φ，θ，ψ］T描述飞机质心的平动和转动运动，φ、θ、ψ分别为飞机的滚转角、俯仰角和偏航角；其次，通过建立起落架模型，计算获得机体与航母平台之间的作用力（包括支反力和弹射力）。对于每一个起落架，分别以［xk，yk，zk］T和 ωk描述其机轮轴线参考点的平动和转动运动，下标k＝｛1，2，3｝分别对应于前起落架、左侧主起落架和右侧主起落架。由于航母运动的动力学特性对飞机弹射起飞过程影响相对较小，故直接通过经验公式描述航母的4自由度运动状态，不再增加航母的动力学方程。为简化和统一描述，下文将统一采用向量和矩阵的形式建立机体和起落架的动力学方程。用于进行仿真计算的模型结构如图1所示。本文采用F/A-18作为算例飞机，其建模数据来源于文献［19-23］。由于篇幅所限，本节中主要对仿真模型各组成部分进行说明，具体模型数据可参见相关引用文献。

图1 非对称弹射起飞仿真模型的结构框图Fig.1 Structure block diagram for asymmetric catapult launch simulation model

1.1 机体动力学方程

作用于飞机质心处的外力有气动力Faero和气动力矩Maero、发动机推力Feng和力矩Meng、起落架作用力Flg和力矩Mlg，飞机质心的平动和转动动力学方程如下：

式中：力和力矩符号的上标表示该力或力矩投影到某一坐标系下的分量，S表示飞机稳定轴系，一般飞机的气动力数据在该坐标系下给出，B表示机体轴系，发动机推力和起落架作用力在该坐标系下定义，I表示惯性系（本文采用北东地坐标系），飞机的平动动力学方程在此坐标系下推导；L为各个坐标系间的转换矩阵；m为飞机的质量；I为飞机转动惯量矩阵；g为重力加速度矢量；p、q、r为飞机的3轴角速度。

1）气动力模型

飞机非线性气动力和力矩系数的数学模型［19-20］如式（2）所示：

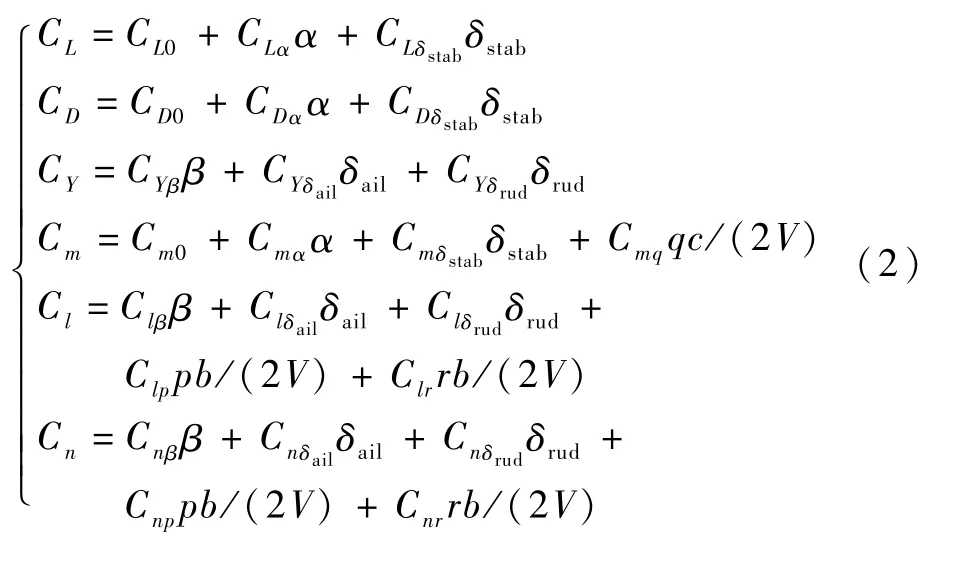
式中：Cnβ为偏航静稳定导数；Cnr为偏航阻尼力矩导数；CL为全机升力系数；α为迎角；β为侧滑角；δstab、δail、δrud分别为全动平尾、副翼和方向舵；b为机翼展长；c为平均气动弦长；V为飞机空速。

由气动力、力矩系数可进一步计算获得飞机的气动力和力矩：

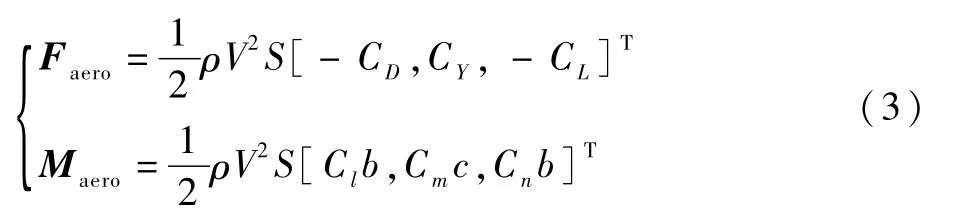
式中：S为机翼参考面积；ρ为海面大气密度。

2）发动机模型［21］

发动机推力 Feng，j和力矩 Meng，j（下标j＝｛1，2｝分别指左、右发动机）的计算公式如下：

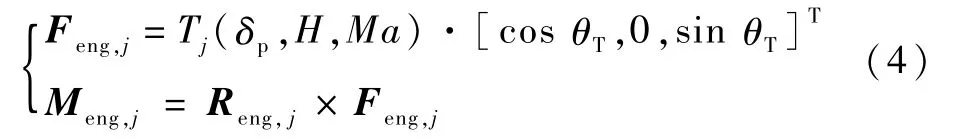
式中：Tj为单台发动机的推力，通常可由油门指令δp、飞行高度H和马赫数Ma插值计算后获得，对于本文中所涉及的弹射起飞工况，Tj固定取值为海平面的起飞推力；θT为发动机的安装角，本文中取 0°；Reng，j为推力作用点到飞机重心的位置矢量，在体轴系下进行表示。

3）质量特性

飞机质量特性数据基于文献［22］得到。由于弹射起飞过程时间短暂，因此在仿真计算时不考虑飞机质量和转动惯量的变化，具体取值可参见表1所给出的基本仿真工况参数取值表。

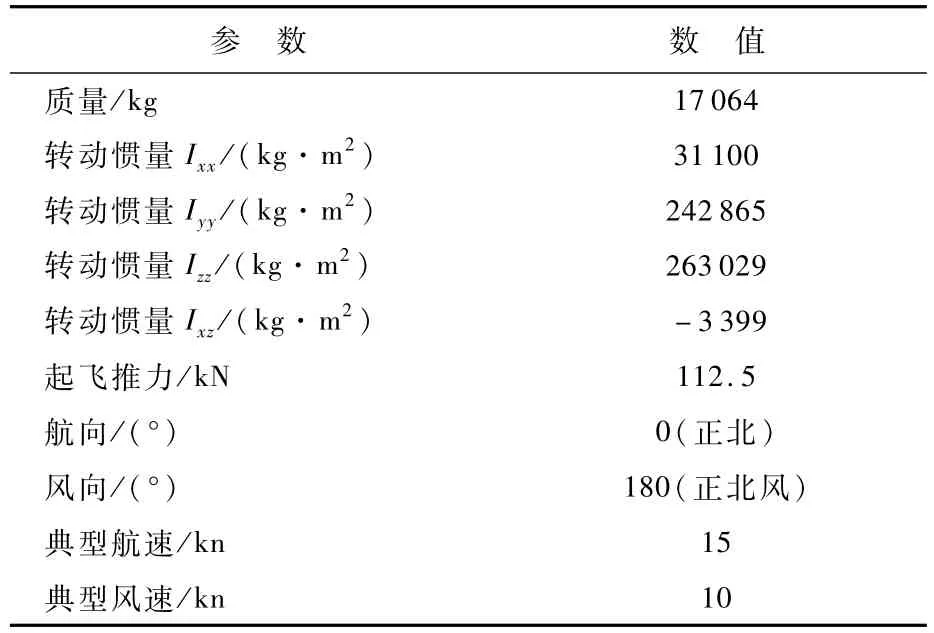
表1 基本仿真工况参数取值Table 1 Basic working condition parameters for simulation

1.2 起落架动力学方程

通过建立各个起落架机轮参考点的4自由度运动方程，可以解算甲板跑道、起落架、机体之间作用力的传递关系［23］。机轮参考点受力情况参见图 2，δk为轮胎压缩量，vx，k为轮胎前进速度，其动力学方程如下：

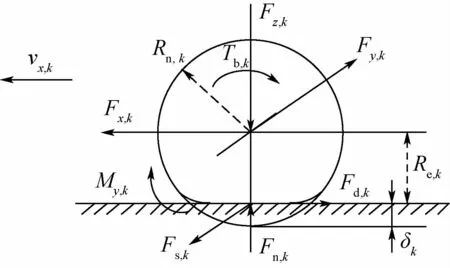
图2 机轮参考点的受力分解Fig.2 Forces and moments at wheel reference point

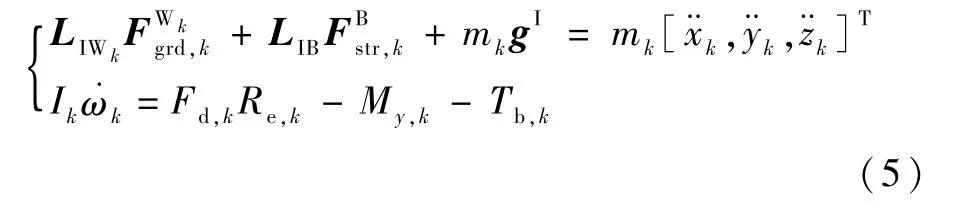
式中：上/下标Wk指起落架机轮参考坐标系；mk为机轮（包括轮胎、轮毂以及刹车装置等非弹性支撑部件）的质量；Ik为机轮关于滚动轴的转动惯量；My，k为轮胎滚阻力矩；Re，k为轮胎的有效滚动半径；Tb，k为作用在机轮上的刹车力矩；Fgrd，k为甲板跑道对机轮的作用力；Fstr，k为起落架支柱对机轮的作用力，作用点近似位于支柱在机身上的安装点。

起落架对于机体的作用力和力矩可表示为

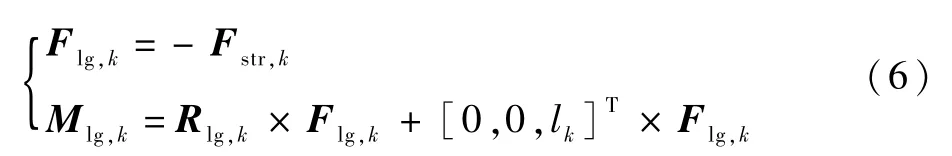
式中：Rlg，k为起落架支柱在机身安装点到飞机重心的位置矢量，在体轴系下表示；lk为支柱压缩后的长度。

Fstr，k由 支 柱 模 型 进 行 计算，其 轴 向 力Fz，k一般由空气弹簧力和油液阻尼力构成，因此可表示为支柱压缩行程及其变化率的函数。基于线性弹性变形假设，支柱的航向力Fx，k和横向力Fy，k可由支柱末端的形变量（即机轮参考点相较于未受力时的位置变化，在机体轴系下表示）进行计算求解。根据以上描述，Fstr，k的计算式如下：

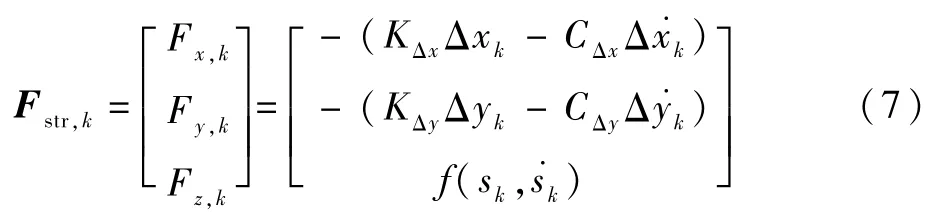
式中：KΔx、KΔy分别为支柱的航向和横向刚度系数；CΔx、CΔy分别为支柱的航向和横向阻尼系数；Δxk、Δyk分别为机轮参考点实际位置与未受力时的位移变化量，这2个变量与支柱径向压缩sk一起可由式（8）进行计算：

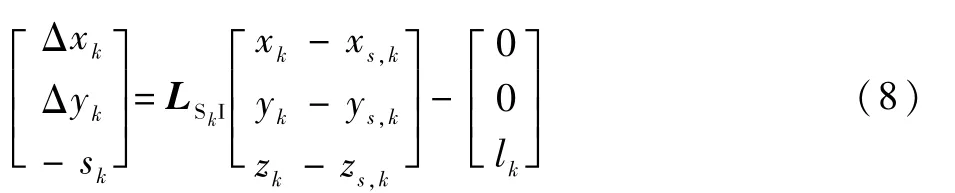
式中：［xk，yk，zk］T为起落架各机轮参考点的绝对位置；［xs，k，ys，k，zs，k］T为起落架支柱安装点的绝对位置，可由飞机的质心位置和姿态角计算获得；LSkI为惯性坐标系到支柱参考坐标系的转换矩阵。

Fgrd，k由轮胎的 径 向 力Fn，k、摩 擦 力Fd，k和 侧向力Fs，k共同组成。轮胎径向压缩受力模型将等效成弹簧阻尼系统，因此可通过轮胎压缩量及其变化率计算径向力。而计算摩擦力和侧向力时所需要的轮胎运动参数，如轮胎前向速度、纵向滑移率、侧偏角、前轮操纵角等，均可通过机轮参考点动力学方程计算的机轮加速度、角加速度结果进一步处理后获得，具体可参见文献［23］。

1.3 航母平台模型

航母平台模型包括了甲板运动和弹射力模型，但不包含航母的动力学方程。航母质心的6自由度运动状态通过以下方式给出：①在水平面内的平动状态［xc，yc］T以航速Vc和航向 χc进行设定；②垂直位移zc和横摇、纵摇、艏摇角［φc，θc，ψc］T则按照正弦形式的经验公式［24］给出（t为时间）：

进一步地，定义以起飞点为原点的起飞甲板坐标系Od-xdydzd（见图 3），其中：Odxd轴与弹射跑道方向一致，指向舰艏方向为正；Odzd轴位于包含Odxd轴的垂直平面内，并垂直Odxd轴指向下；Odyd轴根据右手系定义指向航母右舷。惯性系与起飞甲板坐标系间的转换矩阵可通过欧拉角［φc，θc，ψc+χc+ψr］T进行计算求解，其中：ψr为弹射跑道与航母纵轴的夹角。

基于起飞甲板坐标系，一方面可以灵活配置不同的起飞点位置及弹射跑道方向，便于研究非对称弹射问题；另一方面，将各个起落架机轮参考点与起飞点的相对位置关系投影到该坐标系下，可以获得机轮参考点甲板高度，从而作为轮胎的压缩量及起落架受力情况计算的数据输入。

图3 起飞甲板坐标系Fig.3 Coordinate system of takeoff deck

参考美军标 MIL-STD-2066［25］，选取 C13-1型弹射器数据对弹射力Fcata进行建模，可将弹射力表示为随弹射冲程xcata变化的曲线（见图4）。由于弹射力通过起落架模型传递到机体上，因此其在作用于前起落架上时，将被分解为一个水平向前和一个垂直向下的力，弹射杆与甲板的夹角近似取为30°。

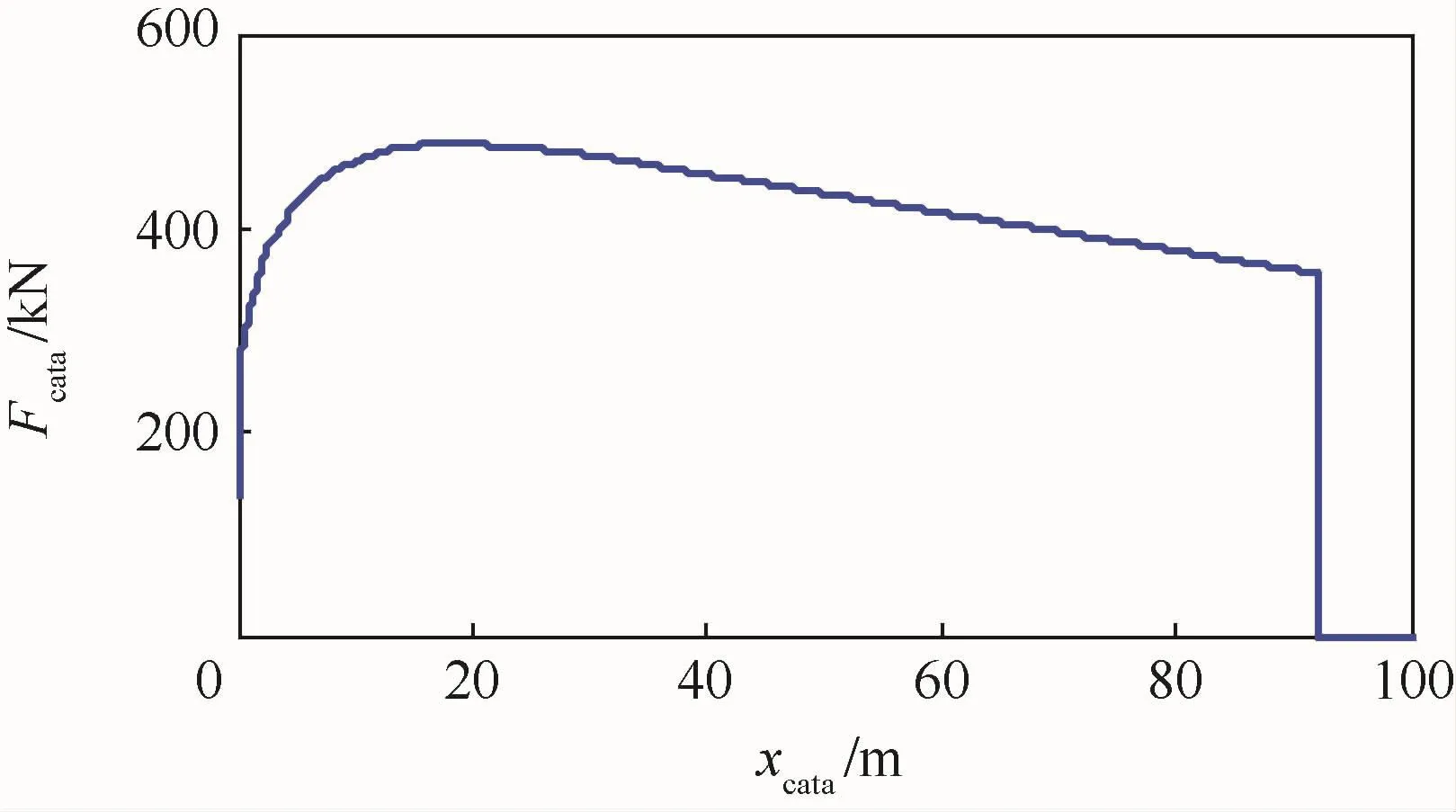
图4 典型弹射力-弹射冲程曲线Fig.4 Typical curve of catapult force versus catapult stroke

1.4 大气环境模型

大气环境模型用以设置弹射起飞时的海面常值风和舰艏气流，其中前者常定义在北东地坐标系下，以风速和风向表示，而后者与航母运动有关，因此一般在航母坐标系下定义。将总的风速矢量合成后，还需要转换到飞机机体坐标系下，用于计算飞机的迎角和侧滑角。一般舰艏气流模型只给出了飞机纵向对称面内的风速，而本文侧重于研究非对称起飞问题，因此仿真计算时将主要考虑起飞过程中的常值侧风。

1.5 仿真计算工况

对于算例飞机，在甲板风风速为25 kn（12.9m/s）的条件下进行对称弹射起飞仿真计算的输入条件如表1所示。飞机主要的纵向飞行状态参数曲线如图5所示（图中“×”表示飞机离舰时刻），其中各参数的变化历程与文献［9］中所给出的试飞数据相符，表明本节所建的弹射起飞数学模型是正确合理的，可用于第2节进一步开展非对称弹射起飞仿真计算。图中：Va为空速。

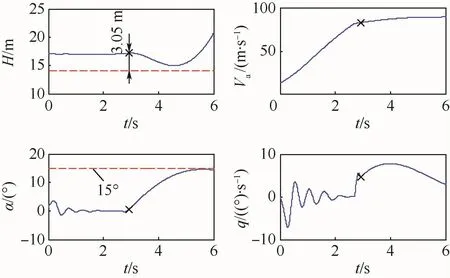
图5 对称弹射起飞仿真Fig.5 Simulation of symmetric catapult launch

2 非对称因素的影响分析

2.1 定位偏心

理想状态下，飞机在弹射道上安装时其机身的轴线方向应与弹射器轨道方向完全重合。而实际上，由于航母的运动以及手动进行飞机滑行操纵等因素影响，飞机往往会出现定位偏心的情况。工程上常采用偏心距加以描述，其定义如下［2］：飞机左右主起落架中点到弹射器轨道的距离，即图6中的yerr。当中点落在跑道右侧时yerr取正值，此时飞机机头指向弹射跑道左侧。图中：F、cg、f分别为弹射力、重心位置、侧向摩擦力；d1和d2分别为飞机重心到前轮和主轮的纵向距离。

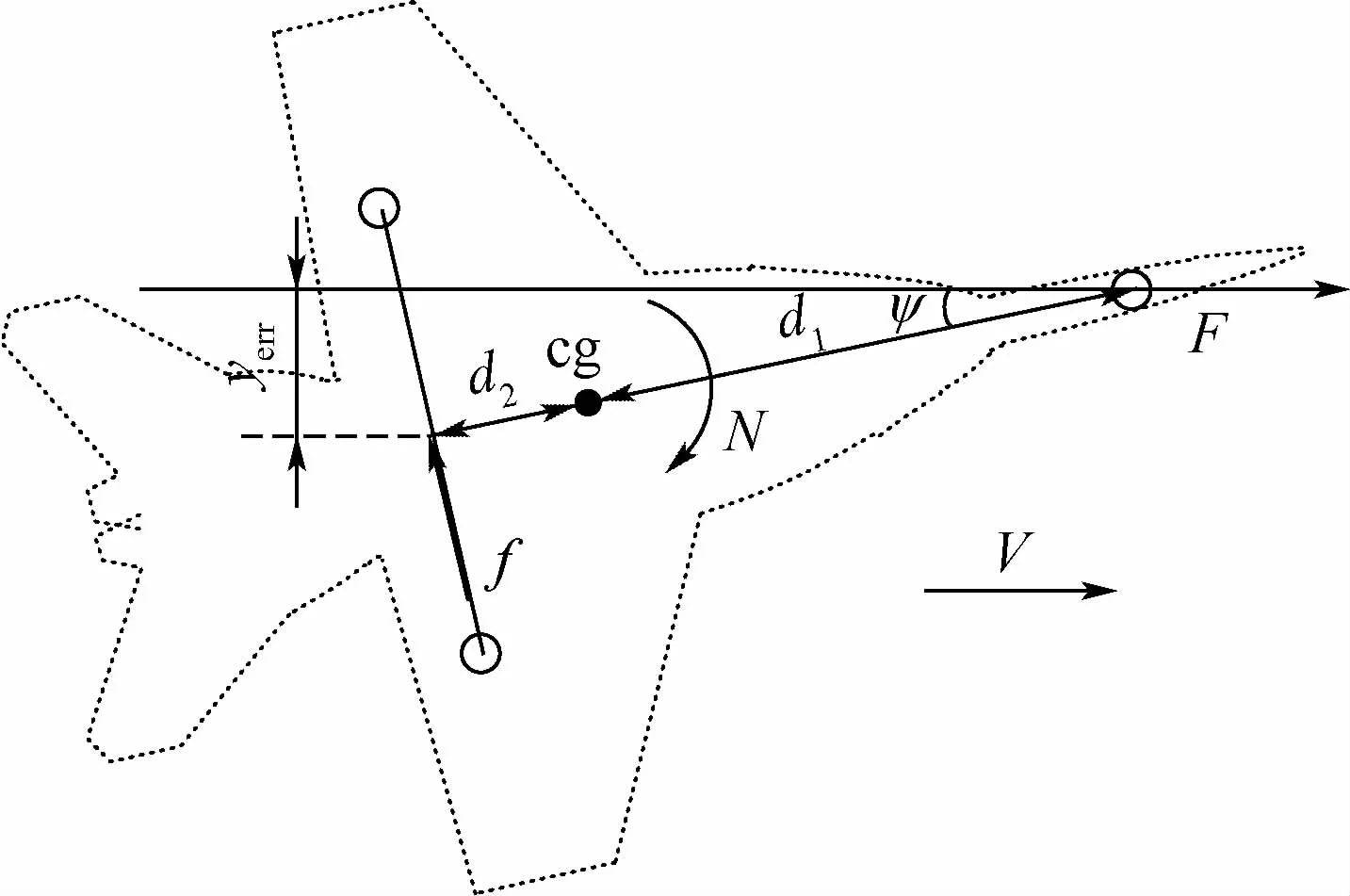
图6 偏心弹射示意图Fig.6 Schematic diagram of off-center position catapult

2.1.1 理论分析

选取偏心弹射过程中的某一时刻，对飞机的偏航运动进行受力分析（如图6所示），其转动动力学方程为

式中：Lc为弹射力产生的偏航力矩；N为气动偏航力矩；Lf为甲板跑道对飞机的侧向摩擦力所产生的偏航力矩。上述各力矩的计算公式分别如下：

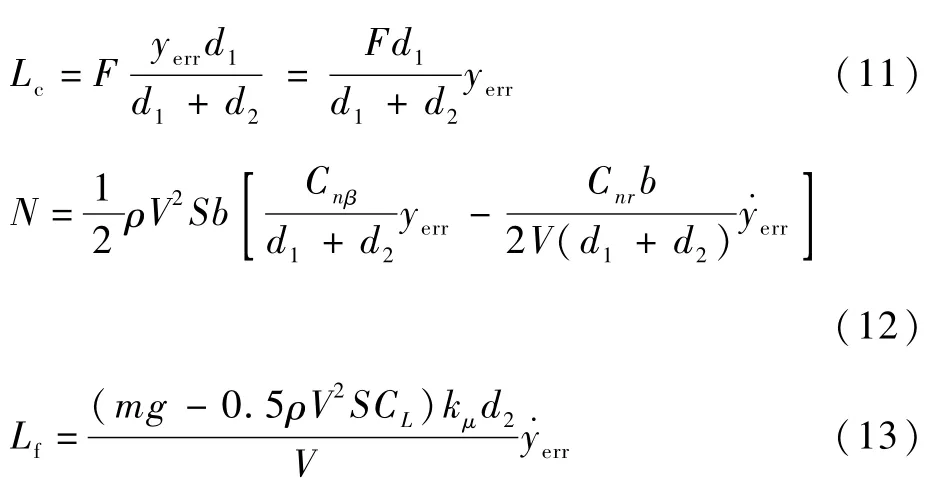
根据几何位置关系，可以得到偏航角与偏心距间的转换公式：此外，采用式（13）计算摩擦力产生的偏航力矩时，由于前轮承载相对较小，因此可以将全机所受的侧向摩擦力f等效在左右主轮的中点处，并由起落架的轴向载荷与侧向滑动摩擦系数μs计算获得。其中，μs一般是关于轮胎侧偏角的函数，在小范围内可近似地认为二者间呈线性关系，

斜率为kμ，即

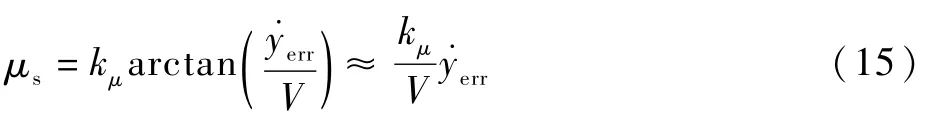
对于飞机的偏航角速度r和侧滑角 β，可以通过偏航角ψ及其微分加以近似描述，并由式（14）写成关于yerr的表达式。代入并进行整理后，式（10）可进一步写成形如式（16）的关于偏心距yerr的二阶微分系统：

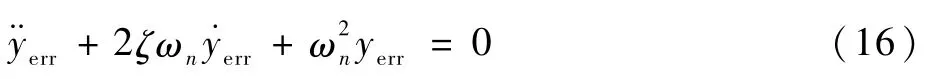
式中：ωn为偏航振荡频率；ζ为偏航振荡阻尼比。二者的计算公式分别为

由式（17）和式（18）可知，偏航振荡频率、阻尼比与弹射力和空速相关，因而在弹射过程中随弹射时间和距离不断变化。其中，振荡频率与弹射力和偏航稳定性2项有关，而偏航阻尼比则由侧向摩擦力和偏航阻尼2项构成。

取典型的弹射力、空速与弹射冲程的变化曲线（见图4和图5），以及典型起飞状态下的飞机质量和惯性矩（见表 1）、气动导数（Cnβ取 0.088，Cnr取 -0.078；CL取 0.25）及侧向摩擦力建模参数（kμ取 3.5）一起代入式（17）和式（18）中进行计算，可以获得随弹射距离变化的振荡频率和阻尼比变化规律，如图 7所示。图中：ωn（F）、ωn（Cnβ）、ωn（F，Cnβ）分别为弹射力、偏航静稳定导数以及二者同时作用时对飞机振荡频率的影响；ζ（kμ）、ζ（Cnr）、ζ（kμ，Cnr）分别为侧向摩擦力、偏航阻尼力矩导数以及二者同时作用时对飞机阻尼比的影响。

根据以上结果，可将定位偏心对弹射起飞特性的影响规律进行小结：

1）偏航振荡频率主要由弹射力-弹射冲程的曲线特性及机体绕z轴的转动惯量决定，通常在2.0～2.5 rad/s之间，即周期为 2.5～3.1 s。由于一般弹射持续的时间为2.5～3.0 s左右，因此弹射结束时飞机的偏航振荡运动恰好经历了约一个周期的振荡变化，其重心仍在初始偏离的一侧。

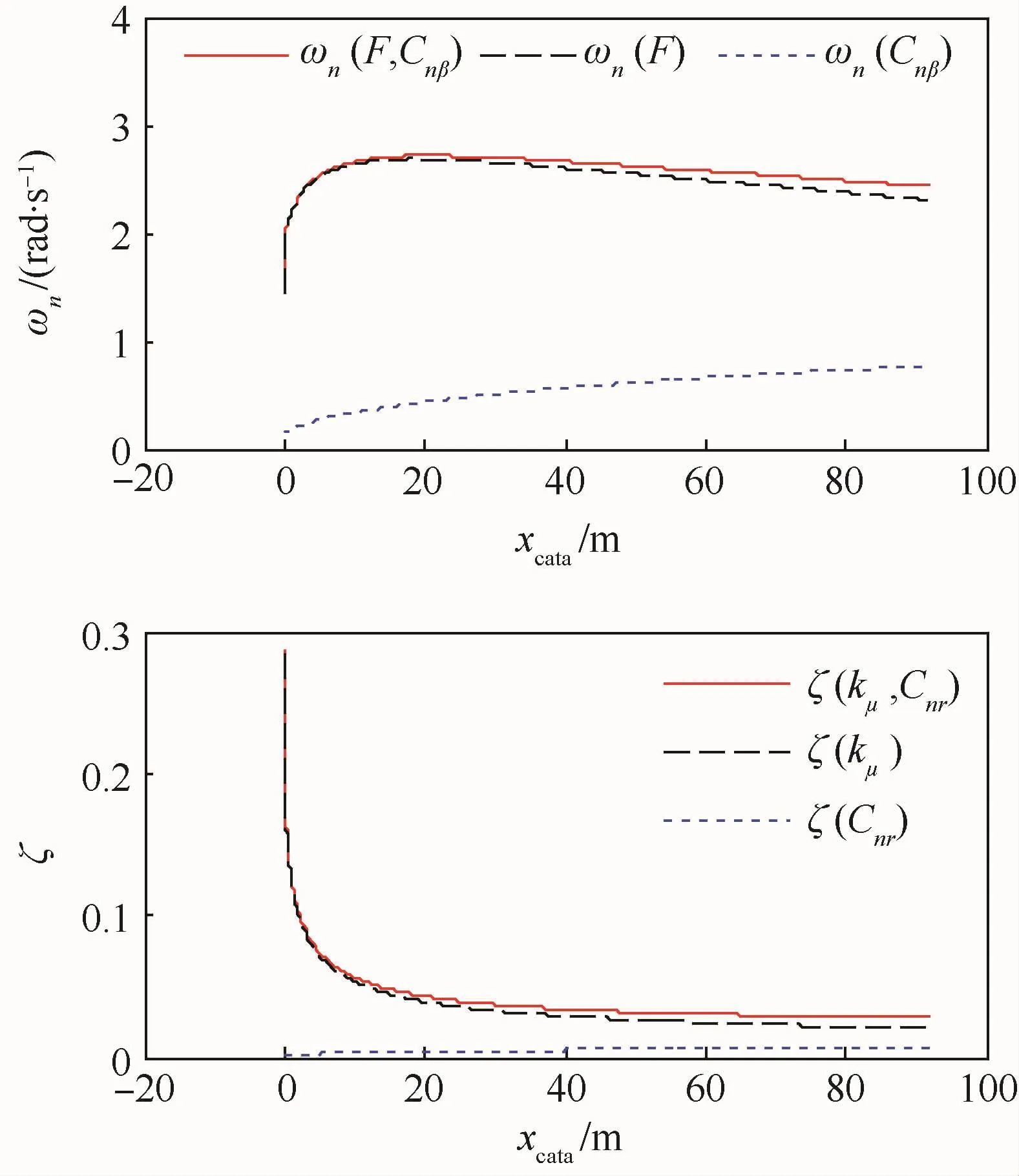
图7 偏航振荡频率与阻尼比随弹射冲程的变化关系Fig.7 Yawing fluctuation frequency and damping ratio versus catapult stroke

2）偏航振荡运动的阻尼主要由甲板跑道对起落架的侧向摩擦力提供，但随着弹射距离增加而迅速减小，这是由于在空速增加后，作用于起落架上的载荷减小，同时轮胎侧偏角也减小。

3）飞机本体的航向稳定性对偏航振荡的影响在空速增大后才逐渐显现，其对频率和阻尼的贡献大约为弹射力、侧向摩擦力的1/4～1/3。

2.1.2 仿真验证

参考有关偏心弹射试验［12］，进行仿真计算时分别将初始时刻的偏心距yerr设置为 0、0.3、0.6m，仿真结果如图 8所示，“×”表示飞机离舰的时刻。

由图8的仿真结果可知：

1）定位偏心使飞机在甲板弹射段出现了沿弹射道偏摆的振荡运动，在离舰前该振荡经历了约1.2个周期，故离舰时飞机重心仍在初始偏差一侧。此外，该振荡运动的频率和阻尼与初始的偏心距离大小无关，这与前述的理论分析结果相符。

2）对于偏心距为0.6m的情况，尽管飞机在离舰时刻的滚转角不超过0.5°，同时滚转角速度也小于2（°）/s，但在离舰后飞机滚转角却快速增大至近15°，并且航迹向出现滚转的一侧偏离，原因在于：偏摆运动使飞机离舰时的偏航角速度为3.4（°）/s，这一角速度一方面通过飞机气动导数Clr使飞机正滚，同时使机头右偏产生负侧滑，在横向静稳定导数Clβ作用下进一步加剧了滚转偏离运动。

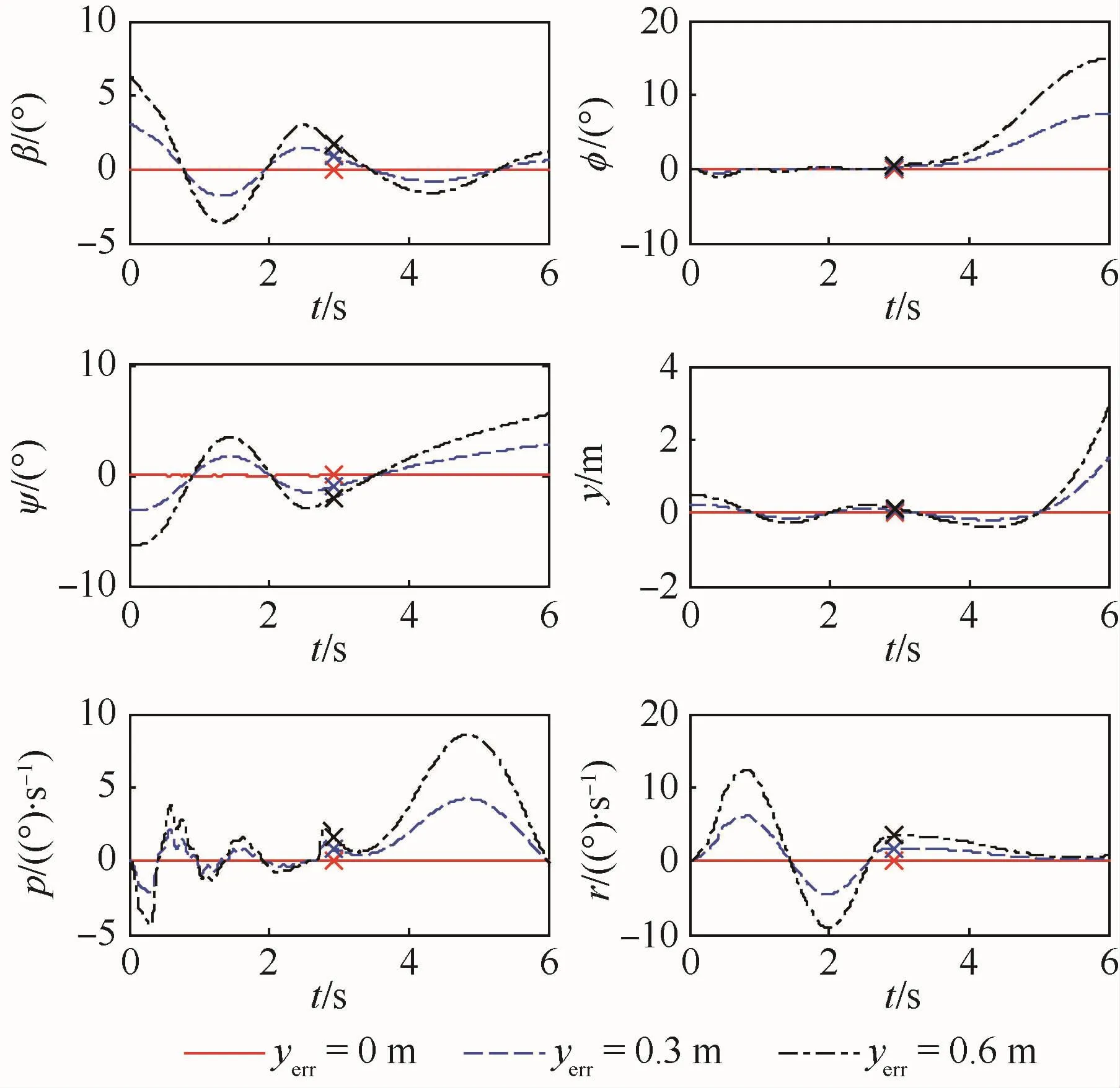
图8 不同偏心距对弹射起飞的影响Fig.8 Effect of different off-center positions on catapult launch

2.2 弹射道偏角

2.2.1 理论分析

飞机从斜角甲板上进行弹射时，弹射跑道方向与航母纵向轴线方向存在某一固定的偏角，因此飞机的空速方向与机体对称面方向并不一致，产生的侧滑角将使飞机发生侧向航迹偏离。分析这一问题时，首先需要说明在弹射滑跑和离舰上升2个阶段飞机空速的计算方法。

由飞行力学的基本定义可知，飞机的地速VE、空速VA以及环境风速VW三者之间的计算关系如下：

甲板风是航母在进行舰载机起降作业时重要的工况参数，它表示一种相对风速的概念，即甲板上所感受到的风速矢量，相当于航母的“空速”。因此，舰速VS、甲板风风速VWOD和环境风速VW也存在对应的计算关系：

联立式（19）和式（20）可得

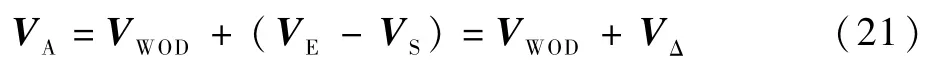
式中：VΔ为飞机与航母之间的相对速度。由于飞机是在弹射器拖梭的牵引下沿弹射器轨道进行加速，因此VΔ将始终沿弹射道方向。

由本节可知，当飞机在甲板弹射滑跑时，离舰时空速应当按式（21）进行计算，并用于弹射器能量的设定［25］。当飞机离舰后，其空速则应该按式（19）计算。

考虑海平面无风，飞机从斜角甲板上进行弹射的情况，此时弹射道指向舰艏左舷，角度取为8°。由于初始时刻飞机空速与船速一致，故空速与机身对称面存在一定夹角（即飞机的侧滑角），并且数值上等于弹射道偏角。弹射开始后，随着机舰相对速度（始终沿弹射道方向）的增加，侧滑角逐渐减小，直至飞机离舰后减小至零。上述的分析表明，当弹射器轨道不完全平行于航母中心线时，飞机在弹射过程中就将始终存在侧滑，由此产生的气动力将影响飞机的横航向运动状态，使其在离舰时出现一定的侧滑和滚转。

分别取4种弹射道偏角与海面风的组合条件（工况 1～4见表 2），对弹射初始时刻和离舰时刻飞机的侧向受力进行对比分析，并将结果整理在表3中，获得的主要结论如下：

1）无风情况下（工况1和2），只要弹射道存在偏角，那么在甲板弹射阶段就会受到侧力影响，但随着空速增大侧滑角减小，离舰上升时将不再有侧力。

2）若海平面存在常值风（工况3），那么可以根据海面的风速风向对航速航向进行调整，使得甲板风方向与弹射道方向一致。这样可以保证弹射过程中没有侧向扰动，但离舰上升后飞机仍将受到海面侧风的影响。

3）只要甲板风角度与弹射道角度不一致（工况2和4），那么飞机在弹射滑跑段就会有侧向扰动。而离舰上升段侧风影响的大小，将取决于飞机航向与风速方向。

表2 不同弹射道偏角与海面风的组合条件Table 2 Combined conditions of different catapultrunway angles and sea wind

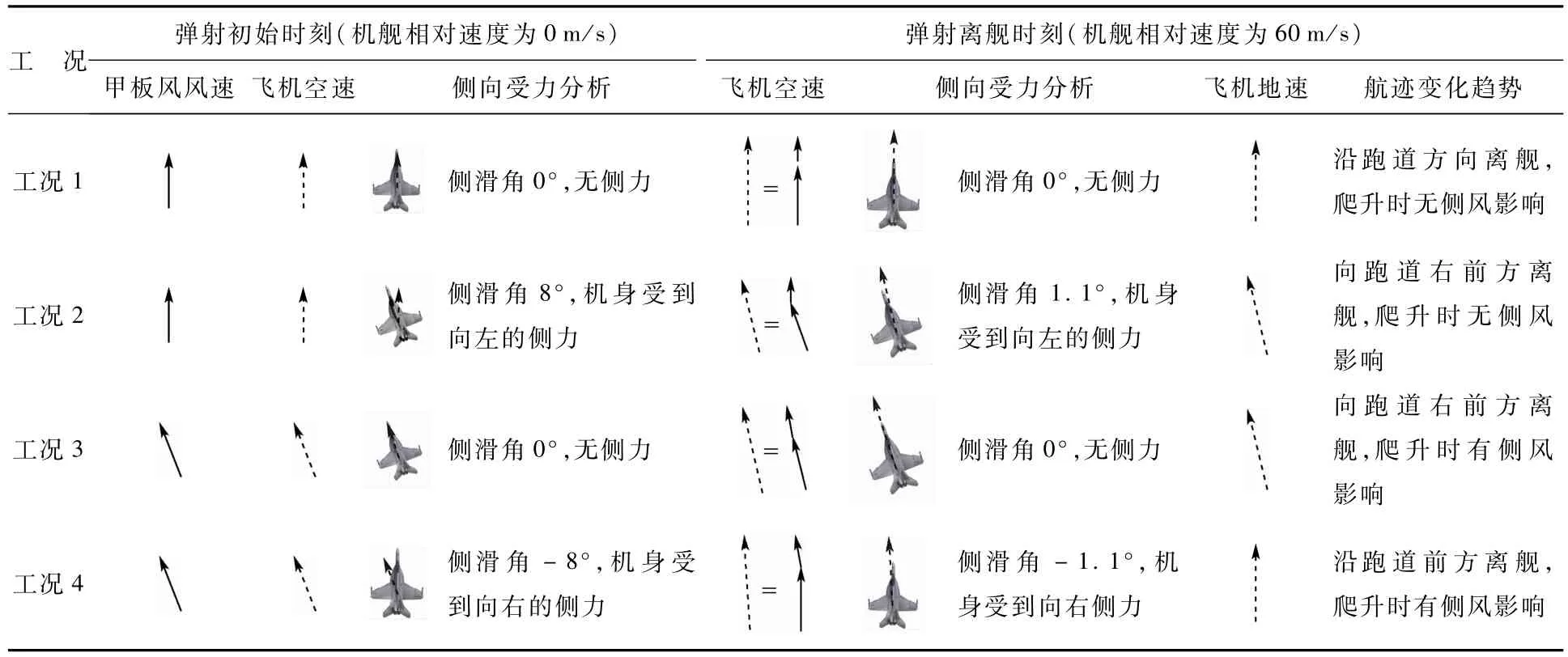
表3 不同工况的弹射过程分析Table 3 Catapult process analysis for different working conditions

2.2.2 仿真验证

按表2中确定的工况分别设置仿真初始条件，仿真结果如图9所示，“×”表示飞机离舰时刻。

由图9的仿真结果可知：

1）8°弹射道偏角引起的侧向扰动，使飞机出现不超过 0.5°的小幅滚转，以及最大为 2（°）/s的偏航角速度。由于弹射滑跑阶段飞机动压较小，因此射道偏角引起扰动力和力矩的影响作用有限，飞机在离舰时的滚转和偏航角速度基本为零，其离舰后的偏离运动能够较快地收敛。

2）8°弹射道偏角引起的侧向扰动程度，与1.4m/s正侧风引起的侧向扰动程度基本相当。由于弹射作业需要考虑最大的侧风为7.5m/s的情况［10］，而一般航母弹射道偏角均不超过 8°，因此弹射道偏角对飞机起飞的安全性影响较小。

2.3 甲板横摇

航母航行时，海面风浪将使其产生俯仰、横摇和偏摆运动，通常可采用纵摇角、横摇角和艏摇角来表征。就弹射起飞任务而言，甲板的横摇角对飞机离舰时的姿态影响较大。在典型海况条件下 ，甲板的最大横摇角可达5°［26］。文献［4］也指出，舰面横摇对飞机离舰后的航迹和上升率影响较大，并且还会引起飞机出现横侧振荡。

图9 弹射道偏角对弹射起飞的影响Fig.9 Effect of catapult runway angle on catapult launch

2.3.1 理论分析

由于航母甲板横摇的频率要远低于起落架缓冲支柱的频率，故可近似认为飞机的滚转角与甲板的横摇角始终保持一致。那么，离舰时刻的甲板横摇角就是决定飞机离舰后航迹侧向变化程度的重要特征参数。

若飞机离舰时带有滚转角，那么其在离舰后则还具有向滚转一侧的侧滑趋势。在飞机本体航向静稳定性的作用下，飞机的空速将偏离弹射跑道的方向以减小侧滑。

对于从斜角甲板进行弹射的情况，飞机离舰后向右前方的航迹偏离，可能导致其与航母舰艏距离过近并发生碰撞。因此，需要对飞机离舰时的甲板横摇加以限制，从而减小飞机离舰后的侧向航迹偏离。

2.3.2 仿真验证

进行仿真计算时，飞机在离舰时的甲板横摇角 φs分别为 0°、3°和 6°。仿真结果如图 10所示，“×”表示飞机离舰时刻。

由图10可知，对于飞机离舰时甲板横摇角为6°的情况：

1）飞机在弹射冲程段就具有较大的滚转角，并且相位与甲板横摇角保持一致，这使飞机产生了侧滑，并出现绕弹射道的偏摆运动。在离舰时刻，飞机的滚转角和侧滑角分别为 6°和 1.2°，因此其在离舰后即出现较大侧向航迹偏离，2 s后侧偏距离超过3 m，同时滚转角也有进一步发散的趋势，不利于安全的弹射起飞。

图10 甲板横摇对弹射起飞的影响Fig.10 Effect of deck roll on catapult launch

2）由于离舰后飞机始终保持一定程度的滚转姿态，此时滚转角导致的升力损失将使其纵向爬升特性下降。仿真结果表明，算例飞机的航迹下沉量增加了约0.22m。

3 安全甲板风包线

本节将首先讨论弹射起飞安全性的准则要求，其次针对算例飞机建立基本的安全甲板风包线，最后进一步分析偏心距、甲板横摇角等非对称扰动因素对安全甲板风包线的影响。

3.1 弹射起飞安全性要求

Lucas在综合分析了多种机型的多次弹射起飞数据后，提出了舰载机弹射起飞的纵向安全准则［5］，简述如下：

1）航迹下沉量。与离舰时刻的位置相比，飞机重心位置的下沉量不能超过10 ft（3.05m）。

2）迎角。弹射起飞过程中，飞机的最大迎角不能超过0.9CLmax对应的迎角，CLmax为最大升力系数。对本文的算例飞机，限制迎角取为15°。

3）上升率。飞机离舰并达到最大航迹下沉量后的 3 s内，上升率需要达到 600 ft/min（3.05m/s）。若离舰后飞机的航迹无下沉，可不对上升率作限制要求。

结合美国军方最新的海试验证情况及飞行手册可知：①现代舰载机通常采用电传飞控系统，在弹射冲程结束后就将自动跟踪目标迎角进行离舰爬升［14］，飞机自身就具有迎角保护功能，可以有效地防范弹射起飞后的失速危险；②上升率要求是针对剩余可用推力需求提出的［9］，并根据飞行员的反馈意见将纵向加速特性等效为上升率要求［5］，以使舰载机获得足够的加速性能。对于现代舰载机，通过开启加力状态可获得更大的起飞推重比和纵向加速特性，因而上升率要求往往比较容易满足。同时，根据已有的试验结果［9］，飞机在弹射后一旦满足了航迹下沉量要求，那么也就都能够满足爬升率要求。

因此，纵向弹射起飞最主要的安全性要求为航迹下沉量。此外，由于本文研究的是非对称因素对弹射起飞安全性的影响，故还需要补充相应的横航向约束要求，即：在离舰后的3 s内，飞机的滚转角应小于5°［14］，这一要求保证飞机的横航向运动状态不会发生显著的偏离。下文中，将基于航迹下沉量和离舰后3 s时滚转角2项指标要求，建立满足弹射起飞安全性要求的安全甲板风包线。

3.2 舰面作业甲板风范围

舰面甲板风的风速大小和风向范围与航母的航向航速、海面风的风向风速等相关。在确定的海面风速风向条件下，可以通过改变航母的航速和航向，为舰载机的弹射起飞作业提供的所有可能范围的甲板风，如图11所示。该图由式（20）计算获得，计算时分别取海面风速为5、10m/s，风向固定为180°不变（即正北风），舰向正北或偏北方向航行（航速在0～13m/s之间可按需调节）。工程上为了便于读取甲板风范围的边界刻度，通常将其绘制为阶梯状的扇面图。

图11 不同海面风速下的作业甲板风范围Fig.11 Operation WOD range at different sea wind speeds

需要指出的是，在舰面作业甲板风范围内，舰载机的弹射起飞未必是安全的。针对这一可能的舰面作业甲板风范围，基于弹射起飞安全性准则，通过仿真计算才能最终确定舰载机的安全起飞甲板风包线的大小。

由图11可知：当海面存在10 m/s的常值风时，最大甲板风可达25m/s，但此风速下风向角只能在355°～5°间变化。如果弹射工况所要求甲板风风速降低，那么风向角的选择范围就能够扩大，通常在330°～30°之间。若是海面常值风减小（例如5m/s时），那么相应地甲板风风速和风向条件也将受到限制。

此外，即便在相同的甲板风条件下，由于海面风速不同，因此获得该甲板风条件时的海面风速与航母航速航向的参数组合关系也就不同。以图11中A点为例（甲板风风速为14m/s，甲板风风向为5°），其对应的参数组合为：若海面风速为5m/s时，则要求航母的航速为 9.1 m/s，航向为346°；若海面风速为10m/s时，则要求航母的航速为 4.0 m/s，航向为 352°。由于飞机在离舰后受到的海面风影响不同，其横航向运动特性亦将有所变化。因此，对于不同的海面风速情况，需要分别计算对应的安全甲板风包线。

3.3 安全甲板风包线的计算方法

基于3.1节给出的弹射起飞安全性要求和3.2节给出的作业甲板风范围，通过仿真计算，可获得算例飞机的安全甲板风包线，从而为弹射起飞作业提供参考。这一过程的计算步骤如下：

1）根据海面风速值，计算获得如图11所示的作业甲板风范围。

2）按照计算精度的要求，将该甲板风范围离散化，获得航向、航速与风速、风向间的参数组合集。

3）对参数组合集中的每一组参数组合条件，进行弹射起飞仿真，并计算离舰后3 s时的滚转角以及最大航迹下沉量，判定是否满足弹射起飞安全性要求。

4）绘制出满足弹射起飞安全性要求的甲板风范围，即为对应约束条件下的安全甲板风包线，如图12所示。

由图12给出的仿真计算结果可知：

1）安全甲板风包线由满足航迹下沉量要求的边界和满足滚转角要求的边界取交集后确定（图 12（b））。但在海面风速较小时（图 12（a）），由于飞机离舰后所受的侧向扰动较小，在试验可取的甲板风范围内均能够满足滚转角小于5°这一约束要求。

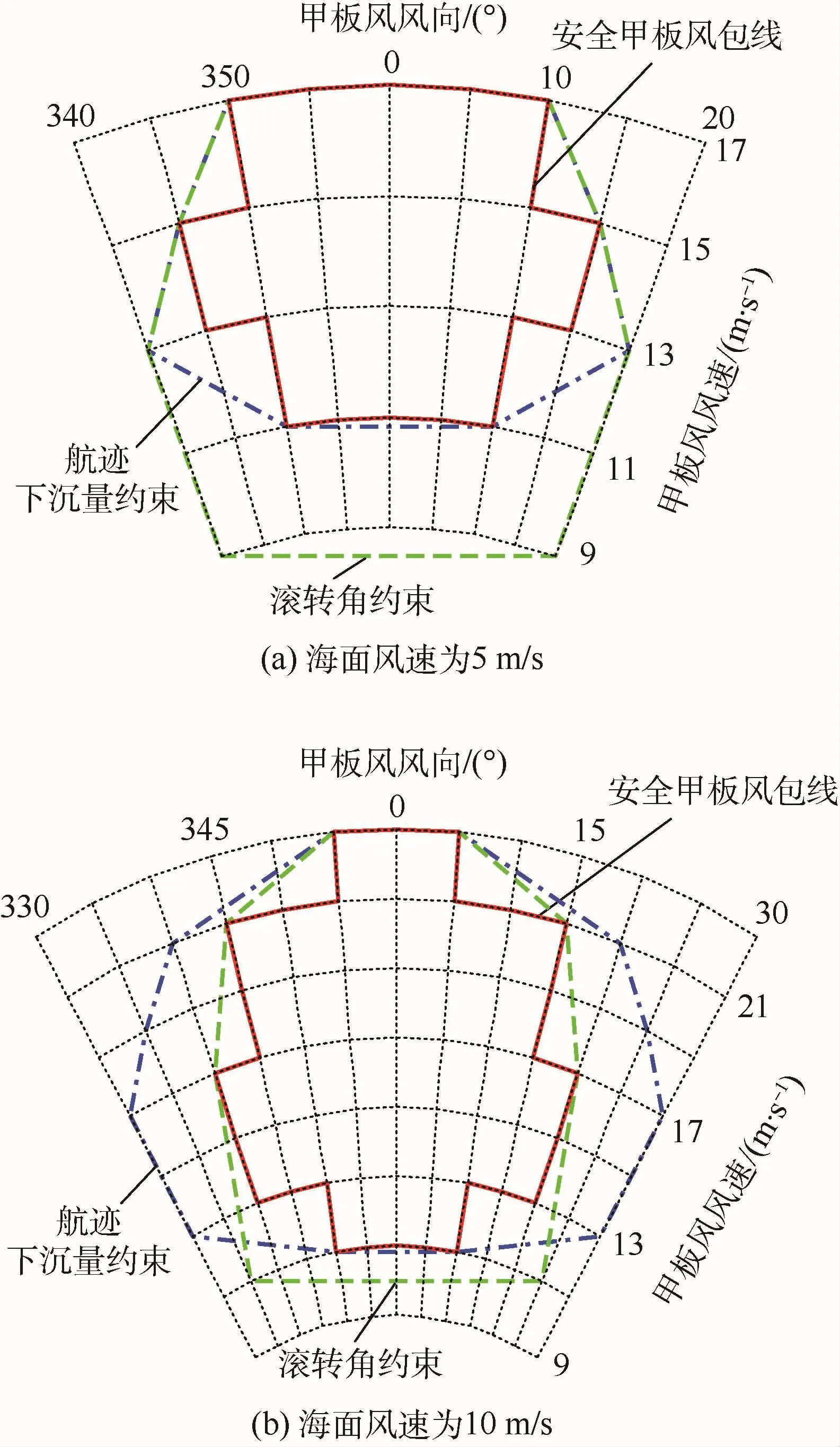
图12 不同海面风速下安全甲板风包线Fig.12 Safe WOD envelope at different sea wind speeds

2）安全甲板风包线的下边界由航迹下沉量确定，即必须保证一定的甲板风风速大小；左右边界基于滚转角的约束，要求甲板风向不能偏离过大；上边界则取决于海面常值风大小，风速越大，飞机初始的空速也就越大，有利于提高弹射起飞的安全性，因此全甲板风包线也就越大。

3.4 偏心距与横摇角的影响

在进行弹射作业时，往往难以完全消除定位偏心、甲板横摇等扰动因素，因此需要定量计算这些扰动因素对弹射起飞安全性的影响，确定允许的偏心距误差、甲板横摇条件要求，从而为提高弹射作业的安全性提供参考依据。在3.2节中给出的计算流程基础上，分别加入 ±0.2m的偏心距和±2°的甲板横摇角作为仿真计算条件，即可得到偏心距、横摇角对安全甲板风包线的影响，如图13所示。

如图13所示，偏心定位与甲板横摇均加剧了飞机的横航向运动偏离趋势，使安全甲板风包线的风向和风速范围显著缩小：

1）对于 ±0.2m的偏心距误差（图 13（a）），安全甲板风包线的最大风向范围缩小至350°～10°，同时风速大小减小至 11～17m/s。

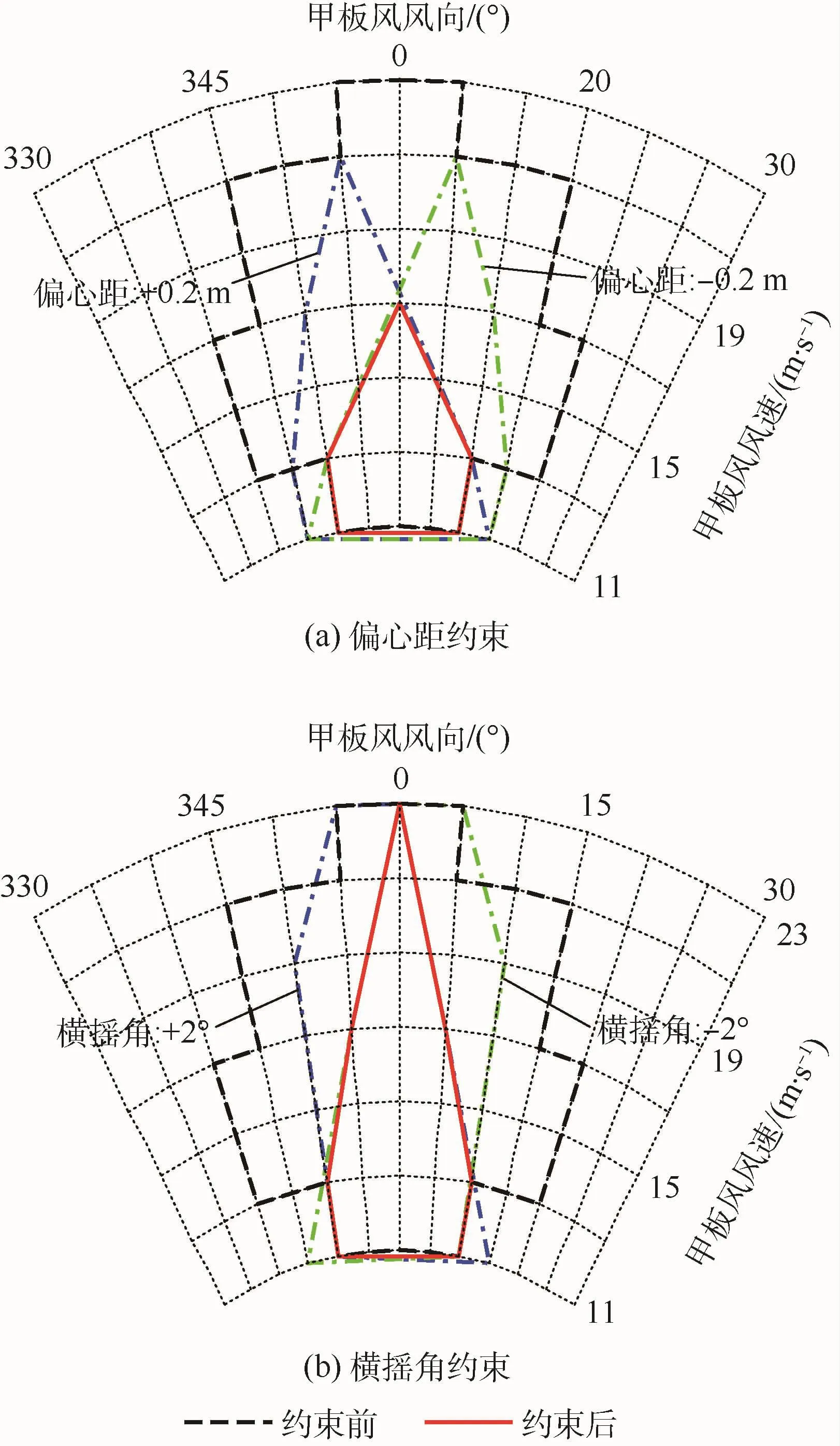
图13 非对称因素对安全甲板风包线的影响Fig.13 Effect of asymmetric factors on safe WOD envelope

2）对于 ±2°的甲板横摇角扰动（图 13（b）），安全甲板风包线的最大风向范围同样将缩小至350°～10°，虽然包线内的最大风速仍可达到23m/s，但此时必须严格约束风向角为0°。

4 结 论

1）定位偏心使飞机在甲板滑跑时出现偏摆运动，该运动的频率主要由弹射力-冲程距离的特性以及偏航转动惯量共同决定，而阻尼则与轮胎侧向摩擦系数相关，但在空速增加后阻尼迅速减小。这一偏航运动将使飞机在离舰上升时出现滚转姿态偏离，不利于弹射起飞的安全。

2）飞机从斜角甲板上进行弹射时，弹射道偏角会引起侧向扰动，使飞机产生横航向运动。但由于一般航母弹射道偏角均不超过8°，故在此范围内进行弹射起飞作业，对飞机安全性影响较小。

3）甲板横摇使飞机在离舰时具有一定的滚转运动，飞机离舰后这一滚转运动会继续缓慢增大，不仅会导致飞机出现较大侧向航迹偏离，也会增大其纵向航迹的下沉量。

4）安全甲板风包线的下边界由航迹下沉量约束，左右边界由滚转角限制确定，上边界由最大海面风速决定。定位偏心误差与甲板横摇扰动等非对称干扰会导致飞机安全起飞的甲板风包线明显缩小。

（References）

［1］聂宏，房兴波，魏小辉，等.舰载飞机弹射起飞动力学研究进展［J］.南京航空航天大学学报，2013，45（6）：727-738.NIE H，FANG X B，WEIX H，et al.Overview of carrier-based aircraft catapult launch dynamics［J］.Journal of Nanjing University of Aeronautics and Astronautics，2013，45（6）：727-738（in Chinese）.

［2］于浩，聂宏.偏中心定位对弹射过程中飞机姿态的影响［J］.北京航空航天大学学报，2011，37（1）：10-14.YU H，NIE H.Effect of off-center location on aircraft attitude during catapult launch［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37（1）：10-14（in Chinese）.

［3］朱齐丹，刘恒，李晓琳.舰载机偏心情况下弹射起飞研究［J］.飞行力学，2016，34（2）：10-14.ZHU Q D，LIU H，LI X L.Research on carrier-based aircraft catapult launching in the case of different eccentricity［J］.Flight Dynamics，2016，34（2）：10-14（in Chinese）.

［4］王大海，苏彬.舰面运动对弹射起飞特性的影响［J］.飞行力学，1994，12（1）：57-63.WANG D H，SU B.The deck motion effects on the catapult-assisted take-off characteristics of the carrier based airplane［J］.Flight Dynamics，1994，12（1）：57-63（in Chinese）.

［5］LUCAS C B.Catapult criteria for a carrier-based airplane：AD-702814［R］.Washington，D.C.：Defense Technical Information Center，1968.

［6］刘星宇，许东松，王立新.舰载飞机弹射起飞时的机舰参数适配特性［J］.航空学报，2010，31（1）：102-108.LIU X Y，XU D S，WANG L X.Match characteristics of aircraft-carrier parameters during catapult takeoff of carrier-based aircraft［J］.Acta Aeronautica et Astronautica Sinica，2010，31（1）：102-108（in Chinese）.

［7］郭元江，李会杰，申功璋，等.复杂环境下舰载机弹射起飞环境因素建模分析［J］.北京航空航天大学学报，2011，37（7）：877-881.GUO Y J，LIH J，SHEN G Z，et al.Modeling and analyze of the environmental factors of carrier-based aircraft catapult launch in complex environment［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37（7）：877-881（in Chinese）.

［8］严重中，冯家波.舰载飞机弹射起飞上升段的自动控制飞行［J］.南京航空航天大学学报，1995，27（4）：431-438.YAN C Z，FENG J B.Automatic control flight for a carrier based airplane in climb phase during catapult launch［J］.Journal of Nanjing University of Aeronautics and Astronautics，1995，27（4）：431-438（in Chinese）.

［9］WALLACE M M.F/A-18E/F catapult minimum end airspeed testing［D］.Knoxville：University of Tennessee，2002：85-88.

［10］STEN C P.Evaluating fixed wing aircraft in the aircraft carrier environment：AD-A244869［R］.Washington，D.C.：Defense Technical Information Center，1992.

［11］ KELLEY H J.Prediction of yawing stability characteristics of airplanes during catapulting［J］.Journal of the Aeronautics Sciences，1952（19）：529-539.

［12］SMALL D B.Full scale tests of nose tow catapulting［C］∥1st AIAA Annual Meeting.Reston：AIAA，1964：1-11.

［13］于浩，聂宏.舰载机偏中心定位弹射起飞弹射杆载荷分析［J］.航空学报，2010，31（10）：1953-1959.YU H，NIE H.Launch bar load analysis of carrier-based aircraft during off-center catapult launch［J］.Acta Aeronautica et Astronautica Sinica，2010，31（10）：1953-1959（in Chinese）.

［14］Naval Air Systems Command.NATOPS flight manual navy model F/A-18E/F 165533 and up aircraft［M］.Washington，D.C.：Department of the Navy，2008：III-8-2.

［15］WILKINSON C H，ROSCOEM F，VANDERVLIETG M.Determining fidelity standards for the shipboard launch and recovery task［C］∥AIAA Modeling and Simulation Technologies Conference and Exhibit.Reston：AIAA，2001：1-10.

［16］贺少华，刘东岳，谭大力，等.载机舰船气流场相关研究综述［J］.舰船科学与技术，2014，36（2）：1-7.HE SH，LIU D Y，TAN D L，et al.A review of researches on ship airwakes［J］.Ship Science and Technology，2014，36（2）：1-7（in Chinese）.

［17］WANG W J，QU X J，GUO L L.Multi-agent based hierarchy simulation models of carrier-based aircraft catapult launch［J］.Chinese Journal of Aeronautics，2008，23（3）：223-231.

［18］ZHANG W，ZHANG Z，ZHU Q D.Dynam ics model of carrier based aircraft landing gears landed on dynamic deck［J］.Chinese Journal of Aeronautics，2009，22（4）：371-379.

［19］CHAKRABORTY A，SEILER P，BALAS G J.Susceptibility of F/A-18 flight controllers to the falling-leafmode：Linear analysis［J］.Journal of Guidance，Control，and Dynamics，2011，34（1）：57-71.

［20］NAPOLITANO M R，PARIS A C，SEANOR B A，et al.Estimation of the longitudinal aerodynamic parameters from flight data for the NASA F/A-18 HARV［C］∥AIAA Atmospheric Flight Mechanics Conference.Reston：AIAA，1996：469-478.

［21］JOHNSON SA.A simple dynamic engine model for use in a real-time aircraft simulation with thrust vectoring：NASA TM-4240［R］.Washington，D.C.：NASA，1990.

［22］BUTTRILL C S，ARBUCKLE P D，HOFFLER K D.Simulation model of a twin-tail，high performance airplane：NASA TM-107601［R］.Washington，D.C.：NASA，1992.

［23］刘海良，王立新.基于数字虚拟飞行的民用飞机纵向地面操稳特性评估［J］.航空学报，2015，36（5）：1432-1441.LIU H L，WANG L X.Assessment of longitudinal ground stability and control for civil aircraft based on digital virtual flight testing method［J］.Acta Aeronautica et Astronautica Sinica，2015，36（5）：1432-1441（in Chinese）.

［24］郭锁凤，申功璋，吴成富.先进飞行控制系统［M］.北京：国防工业出版社，2003：208.GUO SF，SHEN G Z，WU C F.Advanced flight control system［M］.Beijing：National Defense Industry Press，2003：208（in Chinese）.

［25］ U.S.Department of the Navy.Catapulting and arresting gear forcing functions for aircraft structural design：MIL-STD-2066［S］.Melbourne：Engineering Specifications and Standards，1981：47-54.

［26］SCHUST A P，YOUNG P N，SIMPSON W R.Automatic carrier landing system（ACLC）categoryⅢ certification manual：ADA118181［R］.Washington，D.C.：Defense Technical Information Center，1982.