阐述桥梁设计中梁格法的具体应用
2018-03-27王新秋
王新秋
摘要:文章首先阐述了梁格法的基本原理,而后简要概述了梁格划分原则,并结合某桥梁工程案例,深入分析了网格划分的原则,并详细剖析了内力组合、截面钢筋设计与配置等方面,以期提高梁格法在同类桥梁工程中的运用。
关键词:桥梁设计;梁格法;应用
1.梁格法的基本原理
对于箱型断面而言,其主要是由几个顶板结合而成的工字断面结构,在进行桥梁结构不规则设计或者是因为车道交叉而不得不选择加载不规则形式时,会导致各个结构部分中的工字梁内力存在差异性,为了可以更好的确定内力参数,需在桥梁的各个纵向结构中模拟工字梁,然后可以在结构中加入横向单元连接模拟工字梁的横线,很多情况下为了保证该工作的顺利进行可以设置虚拟单元,以建立一个完善的平面网格结构。
通过交叉系列的组合,能够形成一个有效的受力系统,进而对受力进行全面的分析,该方法通常称之为梁格法。在实践阶段,该方法的主要原理是通过等效梁格的方式代替桥梁的上部结构,从而分析梁格受力以及了解桥梁的受力形式。梁格法建模之后可以准确的体现出整体结构的抗扭性。根据实践经验可以知道,虚拟横向梁体数量、刚度和主梁连接,对所有的结果都存在影响作用。所以在利用梁格法的过程中,应该采取有效的措施划分梁格单元划分,并且计算结构的截面与加载,并且合理的使用该结果数据。
2.梁格划分原则
明确基本计算原理之后需要划分网格,在该项工作开展时,其关键点在于对驱顶支座分布的结构以及上部结构的确定,当相关的数据得到确定后,需要通过力学角度以及具体的实际操作经验,对其进行划分,一般情况下在梁格划分时,需要做好以下原则:梁格网格应该与设计受力线的位置是重合的,要与原型结构的内力是一致的,横向与纵向都要符合要求,从而可以更好的提升荷载静力的灵敏度,保证各个关键部分的形心轴与整体结构的在同一位置上。
3.工程概况
某桥梁工程的标准段宽度尺寸设定为32m,该桥梁的轴线、河床中心线位置处于65°,该项目主要以八跨分二联结构为主,且尺寸设计为:(16m+20m×3)+(20m×3+16m),该河道两侧中的线路规划和路幅都已经明确,在两侧中桥两端的一跨、八跨边梁都布置在交叉口位置上。为了可以确保桥梁和道路连接更加的顺畅,可以在两侧边跨使用16m现浇异形结构形式,其中,中间结构的部分采用的是混凝土空心 结构方式,高度设定采用0.95m,在实践过程中,为了能够切实提高工程质量,在现浇板设计时,其高度需控制在80cm,此外,该项目工程为了提高整体工程的稳定性、质量,在设计时应用了梁格法对其结构进行全面分析,且在空间计算时采用(midas/civil2006)软件进行相关数值计算。
4.网格划分
网格划分过程,首要工作需要进行建模,而建模工作开展必须要遵循以下原则:
1)梁格纵梁与原桥梁腹板结构中心线腹板中心线重合,然后通过腹板剪力通过该位置中的梁格剪力来代替。
2)对截面进行计算、确定,并且将获取的截面参数作为单元节点内容,而其他的单元部分按照3m、4m的要求标记相信的点,以使得最终检测数据符合准确性的要求。
3)为了能更加方便设置支座预偏心,可以在系统中明确一个虚拟中梁结构,该结构与实际边总量直接组成一个单元结构,按照支座偏移可以直接分成两个单元,在新增加的节点位置上设置支座结构,以更好的反映出具体的结构特点,然后将实心板的支座两侧进行16等分,连接各个等分点,此时可以将该实心板直接分成16个相等的结构,每个结构都含有一根梁,也就是梁格内的纵梁;实心板自由等分之后连接各个点,就形成了横梁结构。
5)冲击系数结构基频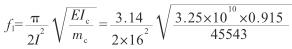
冲击系数 μ=0.17 67×1n(4.957)-0.0157=0.267
4.1内力组合
(1)效应组合
在桥梁结构中的承载性能极限状态计算的过程中,此时可以通过基本组合与偶然组合的形式,本次设计并未考虑柔然组着的影响,所以只利用基本组合进行计算。(2)正常使用下极限效应组合形式。依据桥梁设计技术文件中的作用短期效应组合与长期效应组合,经过计算之后可以确认,短期的最大弯矩需要>949kN·m,而长期效应弯矩则等于904kN·m。
4.2截面钢筋设计与配置
4.2.1配筋设计
以矩形截面的形式布置縱向钢筋。因为各个结构部分中截面尺寸基本相同,本次计算中以弯矩最大截面中钢筋布置为基础来进行估算,其他梁体结构都按照该截面进行数据的计算,符合相应的设计规范要求。
4.2.2钢筋布置(1)跨中纵向钢筋,在设置钢筋时,要结合上述计算的参数进行合理布置,此时确定每束钢筋的设置间隔距离设定为10cm。在本项目中,钢筋布置主要是在16号梁跨中截面,同时,按照设计的要求,钢筋的数量确定为30根。(2)附加钢筋,钝角位置上为了更好的抵抗结构扭矩,在该方向上的二等分垂直方向上设置加强筋,通过下述经验公式确定钢筋面积:Agf=k×Ag=0.8×9852mm2。在具体设置中,每束钢筋的间隔距离设定为10cm,同时在每米宽的位置上附加钢筋面积为9818mm2,与经验结果基本相同。钝角底部位置上所承载的支承反力比较大,此时需要在钝角二等分方向上增加钢筋,间隔距离为10cm钢筋为Φ12mm。
4.2.3结构安全验算
(1)正截面承载力验算。通过实践可知,梁体结构钢筋的数量均一致,因此,在对正截面承载力验算时,需要选择跨中弯矩最大的钢筋进行计算,其他部位的钢筋则忽略不计,在验算时需要按照以下配筋率的公式进行:配筋率ρ=100×16 011/(1225×726)=1.8≥45ftd/fsd=0.27。(2)斜截面承载力验算。在对承载力限效应组合结果分析后,可知,最大剪力值出现在第16梁的右侧,为674kN。依据设计要求,由Vn-Sect=0.51×10-3×b×h0=2367kNγ0×Vd=674kN≤kN 由此可知,抗剪截面的验算标准以满足设计要求。而依据规范
Vn-Load=0.50×10-3×a2×ftd×b×h0=756.9kN
γ0×Vd=674kN<756.9kN。在抗剪力验算上可以忽略对其的验算。
4.2.4持久状况正常使用极限状态验算
(1)裂缝宽度验算
在裂缝宽度验算时,通过对短期组合的计算结果分析可知,长效组合的计算方式与裂缝宽度验算的方式基本一致,其基本相同,因为梁1截面短期效应组合值为949kN·m,比较大,所以此时只进行该梁裂缝宽度数据的验算。在梁1底板结构中配置有26 根 Φ28mm钢筋,总截面积为16 011mm2。根据设计规范中的要求σss=Ms/(0.87×As×h0)=93.9MPa
ρ=As/(b×h0+(bf-b)×hf)=0.016682
W f k = C 1×C 2×C 3×σs s / E s×((3 0 + d)/(0.28+10×ρ))=0.124mm<0.2mm。验算结果可知,裂缝宽度均满足设计要求。
(2)挠度验算
通过综合数分析,在整体作用下最大挠度出现在16梁的跨中8.5mm。依据设计规范中规定,则长期挠度值为:
F L = 1 . 4 5×8 . 5 = 1 2 . 3 m m,获取结果相比于16000/1600=10mm取值范围要大,故而,在设计时可以忽略拱度预设,使其能够将自重减轻。而通过FLQ=12.3-8.5=3.8<16000/1600=26.7mm验算结果可知,获取扰度数值满足规范要求。
5.结束语
从上述计算分析可以发现,应用梁格法验算简单实用,最终数据也非常准确,但是应该要注意使用该方法时,对于截面变动过大以及一些存在较大安全隐患的结构应该具体分析,避免造成事故的发生。
【参考文献】
[1]邵样林.梁格法建模在宽箱梁桥静载试验中的应用[J].城市道桥与防洪,2017(08):262-265+27.
[2]崔巍.基于梁格法在桥梁设计中的应用[J].建筑技术开发,2012,39(07):24-25+79.
