基于遗传支持向量机的综合管廊土建工程造价估算方法研究

李 芊， 张 悠

(西安建筑科技大学管理学院， 陕西 西安 710055)

0 引言

综合管廊是指将市政、通讯、给排水等2种以上的城市管线集中敷设在同一人工空间中所形成的一种现代化、集约化城市基础设施[1]。

综合管廊具有保持路容的美观和城市整洁，节约管线维护费用等诸多优点[2]，但前期投资成本很高，其直接成本比传统直埋形式下管线埋设的成本高出将近1倍，这在一定程度上限制了综合管廊的发展。而有效的造价管理可以控制甚至降低综合管廊的整体造价，从而提高投资效益，促进综合管廊的发展。

现阶段对综合管廊造价管理的研究如下： 宋志宏等[3]认为政府应通过制定合理的建设标准，把握恰当的采购时机和采用适宜的发包方式来实现综合管廊投资控制；王岩等[4]分析造成综合管廊工程概算偏差的原因，并提出合理的应对措施；周青等[5]介绍了设计、施工方案对造价的影响及施工阶段的造价控制要点；徐梅凤[6]运用对比分析方法，结合地质、管廊结构、施工工艺、不同截面的长度和造价分析，得出不同管沟截面的综合造价指标；刘杰[7]对综合管廊工程投资估算中各部分内容进行了明确的划分，并介绍了计算方法，但使用的方法仍是利用定额进行计价。

以上文献从不同角度研究了综合管廊的造价管理，多是从管理方法及影响造价的因素等方面进行研究，对综合管廊造价估算方法的研究则较少。造价估算作为项目决策的依据和造价控制的基础，对整个综合管廊工程的造价影响很大。目前综合管廊工程造价估算方法主要有利用定额进行计价和根据综合管廊投资估算指标等进行计价。由于此阶段设计深度不够，一些工程的结构特征难以确定，定额使用易受限制；而投资估算指标法，由于使用简便，是现阶段较常采用的综合管廊造价估算方法，但大多数指标中考虑的何种施工方法及支护措施并没有得到很清晰的体现，指标的适用性不强。

综合管廊属于全地下工程，此类工程建设时间长、投资金额大，具有影响因素多、小样本及非线性的特点，且近几年才开始大规模建设，可以参考的造价数据较少。本文提出运用遗传算法优化参数的支持向量机模型，从SVM参数选择及基于GA-SVM的综合管廊造价估算步骤等进行阐述。

1 遗传支持向量机

1.1 支持向量机

支持向量机SVM(support vector machine)理论采用结构风险最小化原则代替传统统计学习中的经验风险最小化原则，通过寻求结构风险最小来提高学习机的泛化能力，实现了经验风险和置信范围均最小，从而达到在小样本情况下，也能获得良好的统计规律的目的[8]。支持向量机相比其他常用的机器学习方法(如模糊数学、人工神经网络、灰色系统)，能够更好地解决小样本、非线性、高维数以及局部极小点等实际问题[9-11]。SVM的基本原理如下。

对于线性回归问题： 已有训练样本集假设为D={(x1,y1),… ,(xl,yl),l= 1,2,…,n,x∈Rn，yi∈R}，找到某个线性函数

f(x)=w·x+b。

(1)

式中:w为法向量；b为偏移量。

f(x)是用来逼近未知的回归函数，把回归估计问题定义为对一个损失函数进行风险最小化的问题，利用结构风险最小化原则SRM(structure risk minimization)进行风险最小化时，最优的回归函数是在一定的约束条件下的最小化泛函数为

(2)

约束条件：

(3)

对以上的二次优化问题，引入拉格朗日乘子构造拉格朗日泛函，得到原问题的对偶问题为:

(4)

约束条件为:

(5)

在非线性情况下，将高维空间中的向量内积(xi·xj)由某个适当的核函数k(xi，x)替代，对应的回归函数

(6)

1.2 基于遗传算法的SVM参数选择

在实际应用SVM模型时，通常是根据经验选取SVM的相关参数，这存在一定的主观性，而参数的选取直接关系到支持向量机的预测精度。遗传算法GA(genetic algorithm)具有很强的鲁棒性(robustness)和全局优化搜索能力，适合复杂的优化问题。为了提高综合管廊工程估价的精确度，文中利用遗传算法对支持向量机参数寻优[12]。

根据SVM的基本原理，SVM模型参数主要包括不敏感系数ε、惩罚系数C和核函数的类型及其相应参数这3部分，这3部分参数的合理确定将有效提高SVM模型的精度。

遗传算法(GA)的原理源于进化论和基因遗传学原理，是常用的解决搜索问题的方法，它能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最优解[13]。

充分利用遗传算法的强大全局寻优功能、隐含并行性及算法的高度稳定性，对SVM模型参数在参数空间中自动确定最优或者近似最优参数，这样可大大提高SVM模型精度和使用范围[14]。

2 基于GA-SVM的综合管廊造价估算步骤

1)分析综合管廊工程造价估算特征指标，用这些特征指标作为模型的输入向量，收集综合管廊造价数据组成数据集并进行预处理。

2)构建SVM模型，采用遗传算法确定SVM参数，利用训练样本训练支持向量机模型，并利用测试集进行测试。

3)测试模型的估算精度，若误差在 10 %以内，认为估算模型有效，可以利用对新工程造价进行估算。

估算步骤如图1所示。

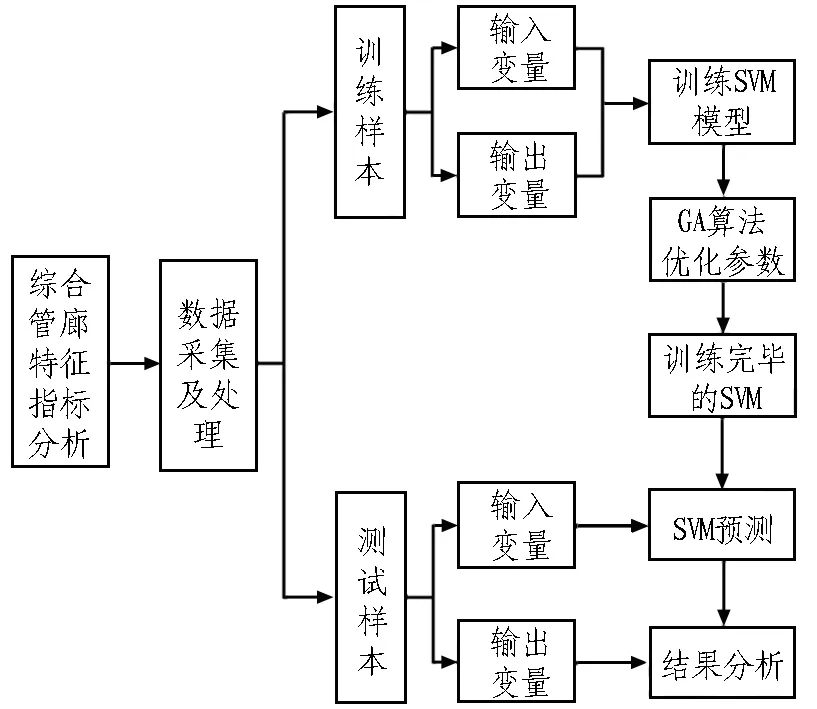
图1 基于GA-SVM综合管廊造价估算步骤

Fig. 1 Procedure of utility tunnel cost estimation based on GA-SVM

2.1 特征指标选取

特征指标的选取应以对工程造价影响较大的、能代表该工程特点的，且影响造价较大的结构特征作为代表工程特征的特征指标[15]。由于综合管廊土建工程费在整体造价中占很大比例，在本文中，以综合管廊土建工程为研究对象。

综合管廊土建工程主要包括主体工程、基础开挖及支护工程。综合管廊是全地下工程，不同的地质条件和建设区域(新旧城区)决定了综合管廊工程的施工方法、围护及防水结构；不同的施工方法决定了地面建筑拆迁的数量、采用的机械及其机械耗量；埋置深度会影响基坑围护、土方、降水工程量以及出入口通道、风道风井等的工程量。综合管廊有多种截面形式，各有其优缺点和适用条件，施工方法也各有不同；截面面积和舱数对混凝土工程量和土方工程量都有很大的影响。建设城市的不同，材料和人工价格存在较大的差异。根据以上分析，选定综合管廊工程造价估算特征指标为综合管廊截面面积和形状、舱数、地质条件、平均埋深、施工方式、支护方式、土石方工程量、建设城区及建设城市等。

2.2 特征数据预处理

综合管廊工程的特征指标主要有字符型与数值型2种。将特征指标作为支持向量机的输入向量时，首先要将其初始化。

字符型特征指标即文字类描述的语言变量，当其作为模型的输入向量时，需要对语言值进行转换使之变成离散的数量值，这样才能使模型识别输入数据。即将其转变为数值型特征指标，对其进行量纲一化处理，但这些数值并没有实际的意义，只是代替文字的一种表示形式。

数值型特征指标的初始化即对其进行归一化处理，可采用通用式(7)，将所有样本的数值型指标转化为[0，1]之间的量，目的是将数据都转化为统一量纲，这样便于计算机识别和SVM模型的接受[16]。

(7)

2.3 模型构建

根据SVM和遗传算法的基本原理，利用SVM建立综合管廊每千米工程造价与特征指标之间的非线性映射关系，把特征指标作为输入变量X=(x1，x2，…，xm)；将工程造价作为SVM的输出变量Y=(y1，y2，…,yn)；利用选取的已建工程的工程特征和造价数据资料作为训练样本进行训练，再运用遗传算法对支持向量机进行参数优化，最后输入测试样本进行预测。

3 算例分析

本文利用Matlab中的SVM工具箱来实现综合管廊工程造价估算模型，以4个城市16条已建的综合管廊工程作为数据库样本，随机选取其中2个为测试样本，余下14个为训练样本，对综合管廊工程造价估算进行仿真。综合管廊工程字符型特征指标量化值如表1所示。根据表1对字符型数据进行量化处理，之后对全部数据进行归一化处理，预处理后的各特征指标数据如表2所示。

选择第10个和第14个数据作为测试样本，其余为训练样本。将预处理后的数据用于模型的训练，并采用遗传算法对参数进行优化。由于这是典型的回归问题，核函数选择径向基核函数。最后对测试样本进行预测，并与实际值对比分析。为了验证本文所建的估算模型，将本文模型与标准SVM模型的估算结果进行比较。标准SVM模型参数设置使用默认设置。估算结果如表3所示。

表1 综合管廊工程字符型特征指标量化值

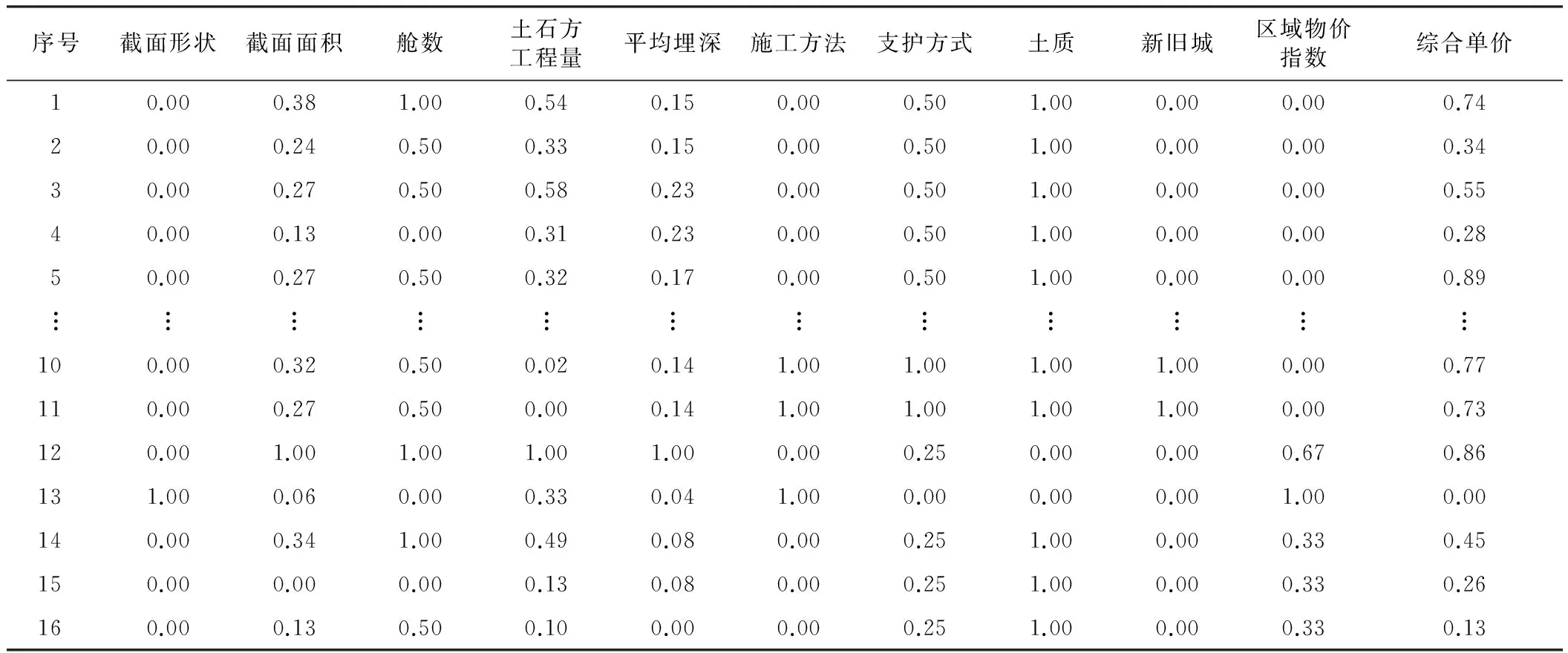
表2 特征指标预处理后的部分数据

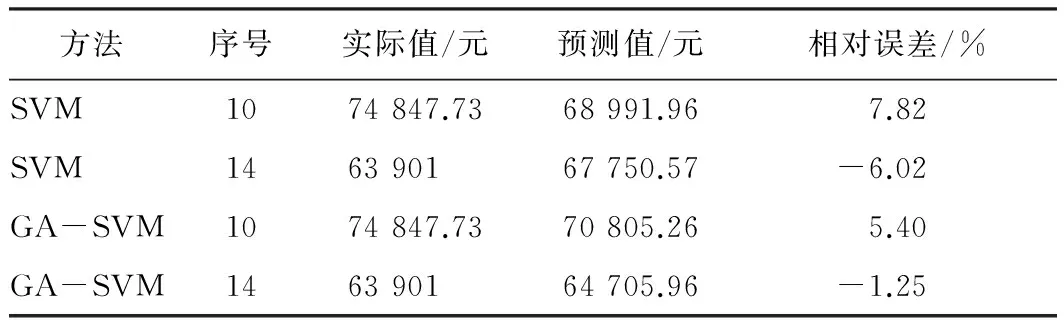
表3 计算结果比较

可以看出，GA-SVM模型的估算误差小于10%，估算精度达到了95%左右，这在工程项目的早期是比较满意的结果了。标准SVM模型的估算误差也小于10%，但GA-SVM模型估算的精确度还是高于标准SVM模型。

4 结论与讨论

本文建立了基于遗传算法优化参数的SVM模型，针对综合管廊工程造价估算影响因素多、小样本及非线性的特点，发挥了SVM处理小样本的非线性回归问题的优势，并运用遗传算法对模型进行优化，提高了估算精度，该模型为综合管廊工程造价估算提供了一种新思路。通过实例分析对比了标准SVM和GA-SVM估算的准确性，验证了本文模型的可行性。

由于本文只选取了 4个城市16条综合管廊作为样本进行分析，特征指标的选取也存在一定的主观性，故本文模型合理性还需要对更多类型和地区的综合管廊进一步研究。随着相关研究的不断深入和完善，该模型必将对综合管廊快速准确的造价估算起到积极的作用。

本文仅对综合管廊土建工程的造价估算进行研究，未涉及综合管廊的设备购置与安装、道路拆除和恢复及入廊管线等费用，故在后续的研究中有待补充，以便得到更完整、准确的综合管廊造价估算。

[1] 董立. 市政综合管廊关键技术研究[J]. 科技创新导报，2012(7): 17.

DONG Li.Research on key technology of utility tunnel[J]. Science and Technology Consulting Herald， 2012(7): 17.

[2] 桂小琴， 王望珍， 章帅龙. 地下综合管廊建设融资的激励机制设计[J]. 地下空间与工程学报， 2011， 7(4): 633.

GUI Xiaoqin， WANG Wangzhen， ZHANG Shuailong.The incentive mechanism for financing of the municipal utility tunnel construction[J]. Chinese Journal of Underground Space and Engineering， 2011， 7(4): 633.

[3] 宋志宏， 冯海忠， 梁舰. PPP模式下综合管廊工程总体造价把控要点[J]. 中国财政， 2016(13): 34.

SONG Zhihong， FENG Haizhong， LIANG Jian.The overall cost control points of the utility tunnel project in PPP mode[J]. China State Finance， 2016(13): 34.

[4] 王岩， 王素军， 韩海荣. 影响综合管廊概算质量的因素分析及对策研究[J]. 工程建设， 2016， 48(2): 66.

WANG Yan， WANG Sujun， HAN Hairong.Research on analysis of the influencing factors and countermeasures for budgetary estimation quality of utility tunnel[J]. Engineering Construction， 2016， 48(2): 66.

[5] 周青， 康良春. 城市地下综合管廊造价控制的要点[J].建筑工程技术与设计， 2016(21): 314.

ZHOU Qing， KANG Liangchun. The main points of urban utility tunnel cost control [J]. Architectural Engineering Technology and Design， 2016(21): 314.

[6] 徐梅凤. 综合管廊造价指标分析[J]. 建材与装饰， 2016(19): 141.

XU Meifeng. Analysis of utility tunnelcost index[J]. Construction Materials & Decoration， 2016(19): 141.

[7] 刘杰. 城市综合管廊工程投资估算研究[J]. 科技创新与应用, 2017(14): 243.

LIU Jie. Research on investment estimation of utility tunnel[J]. Technology Innovation and Application, 2017(14): 243.

[8] 彭光金， 俞集辉， 韦俊涛， 等. 特征提取和小样本学习的电力工程造价预测模型[J]. 重庆大学学报(自然科学版)， 2009(9): 1104.

PENG Guangjin， YU Jihui， WEI Juntao， et al. Cost forecast model for power engineering based on feature extraction and small-sample learning[J]. Journal of Chongqing University (Natural Science)， 2009(9): 1104.

[9] 梁迅. 建筑工程单方造价快速估算方法综述[J]. 广东工业大学学报, 2012, 29(3): 107.

LIANG Xun. Review of the new methods of fast estimation of construction engineering unit square cost[J]. Journal of Guangdong University of Technology, 2012, 29(3): 107.

[10] 王绵斌， 李欢欢， 谭忠富， 等. 基于支持向量机方法的输电工程造价指标评估体系[J]. 电力建设， 2014(3): 102.

WANG Mianbin， LI Huanhuan， TAN Zhongfu， et al. Index evaluation system of power transmission project cost based on support vector machine method[J]. Electric Power Construction， 2014(3): 102.

[11] 蒋淳， 魏雪丽， 陆远忠, 等. 支持向量机在地震综合预测中的初步应用[J]. 中国地震, 2006(3): 303.

JIANG Chun， WEI Xueli, LU Yuanzhong， et al. The support vector machine method and its elementary applications to synthetic earthquake prediction[J]. Earthquake Research in China， 2006(3): 303.

[12] 陈伟根， 滕黎， 刘军， 等. 基于遗传优化支持向量机的变压器绕组热点温度预测模型[J]. 电工技术学报， 2014(1): 44.

CHEN Weigen， TENG Li， LIU Jun，et al. Transformer winding hot-spot temperature prediction model of support vector machine optimized by genetic algorithm[J]. Transactions of China Electrotechnical Society， 2014(1): 44.

[13] 边霞, 米良. 遗传算法理论及其应用研究进展[J]. 计算机应用研究, 2010, 27(7): 2425.

BIAN Xia， MI Liang. Development on genetic algorithm theory and its applications[J]. Application Research of Computers, 2010, 27(7): 2425.

[14] 罗亦泳， 张豪， 张立亭. 基于遗传支持向量机的多维灰色变形预测模型研究[J]. 浙江工业大学学报， 2010(1): 79.

LUO Yiyong， ZHANG Hao， ZHANG Liting.Study of multi-dimensional grey prediction model of deformation based on genetic algorithm and support vector machines[J]. Journal of Zhejiang University of Technology， 2010(1): 79.

[15] 刘浪. 影响高等级公路造价的因素研究[J]. 重庆交通大学学报， 2006， 25(1): 90.

LIU Lang. Research on the factors which influece high-grade road cost of building[J]. Journal of Chongqing Jiaotong University， 2006， 25(1) : 90.

[16] 潘雨红, 张宜龙, 蔡亚军, 等. 基于GA-BP算法的公路工程造价估算研究[J]. 重庆交通大学学报(自然科学版), 2016, 35(2): 141.

PAN Yuhong， ZHANG Yilong， CAI Yajun, et al. Research on highway engineering cost estimation based on the GA-BP algorithm[J]. Journal of Chongqing Jiaotong University(Natural Sciences), 2016, 35(2): 141.