正三角型三芯光纤中等腰对称平面波的调制不稳定性分析∗
2018-03-27裴世鑫徐辉孙婷婷李金花
裴世鑫 徐辉 孙婷婷 李金花
(南京信息工程大学物理与光电工程学院,江苏省大气海洋光电探测重点实验室,南京 210044)(2017年7月18日收到;2017年11月25日收到修改稿)
1 引 言
调制不稳定性(modulation instability,MI)是指加在平面波上的微小扰动随传播距离指数增长的不稳定性行为,它是系统非线性效应和色散效应之间的互相作用导致的对稳态的调制[1−9].在非线性光学领域,MI通常出现在反常色散区,当发生交叉相位调制[10,11]、损耗色散[12]、高阶色散[13,14]以及周期色散调制[15]等时,亦可出现在正常色散区.MI可用于产生高重复率的超短脉冲串[16]、制成调制不稳定激光器、产生时间光孤子新光源[17]、孤子光传输[18]、光开关、超连续光谱、光纤传感[19]、频率转换器[20]等.
基于单模、单芯的光纤通信容量即将达到极限,为满足人们日益增长的对信息传输容量的需求,近年来,人们提出了一种新的光纤通信技术,即基于多芯/多模光纤的空分复用技术[21−24].非线性效应是影响空分复用技术的主要因素之一,近年来涌现出大量有关多芯/多模光纤非线性效应方面的研究工作,包括非线性多芯/多模光纤模型方程的推导、非线性耦合系数的计算、非线性效应对信息传输效率的影响、孤子脉冲在其中传输的稳定性及多孤子相互作用等诸多方面的研究.在MI分析方面,文献中单芯光纤MI的研究已经非常透彻,最新进展包括非均匀光纤MI增益谱分析[25]、高阶效应对MI增益谱的影响[26−30]等研究.多芯光纤方面,目前文献中对双芯光纤MI已经有较系统性的研究[31−40],包括一芯为正折射率材料、另一芯为负折射率材料制备的双芯光纤MI分析及高阶非线性效应和拉曼散射效应对MI增益谱的影响[41,42];相对之下,对芯数大于2的多芯光纤调制不稳定性分析却非常少.
本文使用线性稳定性分析方法详细研究了正三角型三芯光纤中等腰对称平面波MI增益谱的主要特征,分析了不同场分布下MI增益谱在反常和正常色散区域随入射总功率、光纤线性耦合系数以及耦合系数色散的演化规律.
2 耦合模型方程
考虑如图1所示的呈正三角形排列的三芯光纤,其中三芯具有完全相同的特性,波在其中传播的非线性控制方程为:
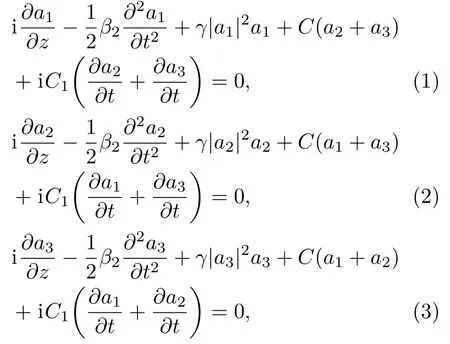
其中aj(j=1,2,3)是第j个芯中电场的慢变包络,z是传播距离,t是时间坐标,β2是群速度色散系数,γ=2πn2/(λAeff)是非线性系数(n2是折射率,λ是载波波长,Aeff是有效光芯面积);C是线性耦合系数,实现三芯中周期性脉冲转换,描述线性耦合系数随入射光频率的依赖关系,其中w是入射脉冲的角频率,w0为中心载波频率.C1又称为耦合系数色散,会导致脉冲展宽甚至分裂现象.
方程(1)—(3)允许等腰对称平面波,即


其中P1,P2和波数k之间的约束关系如文献[43]中(7)—(9)式所示,在此不再重复展示.
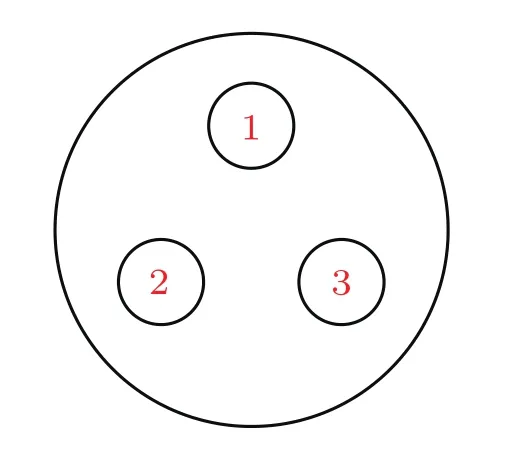
图1 正三角型三芯光纤示意图Fig.1.Scheme illustration of equilateral three core fibers.
设总功率P=P1+2P2,则P≥Pmin,如文献[43]中(10)式所示,Pmin值由线性耦合系数C和非线性系数γ决定.对一给定的总功率P,不同芯中的场分布为

其中s为三阶多项式

的正实数解.
对一给定的三芯光纤,当总功率P从Pmin逐渐增加时,多项式(6)总存在两组不同的正实数s解,同时满足P1和P2的约束关系,不失一般性,令C=200 m−1,γ=5(kW·m)−1,由文献[43]中(10)式知最小总功率Pmin=158 kW,当总功率P从158 kW增加时,芯1和芯2(芯3中场与芯2中场完全相同)中场分布如下.
1)第一种场分布
如表1所列,芯1中的入射功率总大于芯2中的入射功率,即P1>P2,且随着总功率P的增加,P1越来越大,P2越来越小.当改变C或者γ的值时,该场分布规律不变.

表1 C=200 m−1及γ=5(kW·m)−1条件下总功率P与P1,P2数值关系(一)Table 1.The first kind of relationship among P,P1and P2with C=200 m−1and γ =5(kW·m)−1.

表2 C=200 m−1和γ=5/(kW·m)时总功率P与P1,P2数值关系(二)Table 2.The second kind of relationship among P,P1and P2with C=200 m−1and γ =5(kW·m)−1.
2)第二种场分布
当P从最小值158 kW增加时,总的规律是P1越来越小,P2越来越大.当P在158 kW附近时,P1>P2,当P的增加到约180 kW时,出现临界值P1=P2,当P继续增加时,会迅速出现P1<P2,如表2所列,这与上述第一种场分布相反.同样,当改变C或者γ的值时,随P增加,P1越来越小,P2越来越大这一规律不变.
3 MI特性
依线性稳定性分析方法,本文得出与文献[43]中色散关系方程即方程(28)—(34)完全相同的色散关系,这里不再展示.文献[43]实质上只粗糙地分析了第一种场分布时三芯光纤MI增益谱的主要特征,本文则在文献[43]的基础上详细研究两种场分布下三芯光纤的MI增益谱的主要特征,从而完善正三角型三芯光纤中等腰对称平面波的整个调制不稳定性分析.
3.1 第一种场分布
3.1.1 正常色散区
考虑参数C=200 m−1,γ=5(kW·m)−1,相应的最小入射总功率Pmin=158 kW.
图2描述了当β2=0.02 ps2/m,γ=5(kW·m)−1,C=200 m−1,C1=0 ps/m时正三角型三芯光纤等腰对称平面波MI增益谱随总功率P的演化.在最小总功率P=158 kW处有两个MI带,其中高频MI带处于主导地位.随着P的增加,低频MI带增益逐步增强并迅速趋于饱和,而高频MI带增益则迅速减小,同时出现了一个新的微弱增益带.
图2所示的三芯光纤MI增益谱与双芯光纤非对称平面波在正常色散区域中MI增益谱的主要特征非常类似,另外我们发现耦合系数C和耦合系数色散C1对增益谱的影响亦与双芯光纤类似,具体可参考文献[35].其主要区别是对于相同尺寸和材料的双芯光纤,三芯光纤中最小总功率(158 kW)约是双芯光纤最小总功率(80 kW)的2倍.
三芯光纤MI增益谱与双芯光纤增益谱相似的可能原因是由该场的分布特点所决定的,由表1可知P1总大于P2,而且随总功率P的增加,P1≫P2,换言之,相对于芯1中的场,芯2和芯3中的场非常弱,因此,三芯光纤可以等价地看作一个由芯1与芯2组成的双芯光纤,芯3的场可以看作微小扰动,故该场分布下三芯光纤等腰对称平面波的MI增益谱与双芯光纤非对称平面波MI增益谱主要特征相似.

图2 参数β2=0.02 ps2/m,γ =5(kW·m)−1,C=200 m−1,C1=0时,正常色散区MI增益谱随总功率P变化的三维图(a)和二维图(b)Fig.2.(a)3D and(b)2D plots showing the variation of the MI gain spectrum with the total power in the normal dispersion regime with β2=0.02 ps2/m,γ =5(kW·m)−1,C=200 m−1,C1=0.
3.1.2 反常色散区
考虑参数C=200 m−1,γ=2.5(kW·m)−1,相应的最小入射总功率Pmin=316 kW.
图3描述了β2=−0.02 ps2/m,γ=2.5(kW·m)−1,C=200 m−1,C1=0时,MI增益谱随总功率P的演化过程.随着P的增加,该MI增益带逐步增强;并且图3所示的MI增益谱与双芯光纤非对称平面波在反常色散区域中MI增益谱的主要特征非常相似,耦合系数C和耦合系数色散C1对增益谱的影响亦与双芯光纤类似,在此不再展示.同样,其主要区别是对于相同尺寸和材料的双芯光纤,三芯光纤中最小总功率(316 kW)约是双芯光纤最小入射总功率(160 kW)的2倍.
反常色散情况下,三芯光纤等腰对称平面波该场分布对应的MI增益谱与双芯光纤非对称平面波增益谱相似的主要原因与3.1.1节中的分析相同.

图3 参数β2= − 0.02 ps2/m,γ =2.5(kW·m)−1,C=200 m−1,C1=0时,反常色散区MI增益谱随总功率P变化的三维图(a)和二维图(b)Fig.3.(a)3D and(b)2D plots showing the variation of the MI gain spectrum with the total power in the anomalous dispersion regime with β2= −0.02 ps2/m,γ =2.5(kW·m)−1,C=200 m−1,C1=0.
3.2 第二种场分布
3.2.1 正常色散区
考虑参数C=200 m−1,γ=5(kW·m)−1,相应的最小总功率Pmin=158 kW.
图4描述了参数β2=0.02 ps2/m,γ=5(kW·m)−1,C=200 m−1,C1=0时,MI增益谱随总功率P的变化.首先值得注意的是零扰动频率即无扰动初始条件时,MI增益不为零,反而最大;在P=158 kW处,只有一个MI带,随着P的增加,增益不断增强;且在P值增加的过程中,于不同P值临界点出现了两个新生的随着P增加而减小的微弱增益带,但低频MI带始终处于绝对主导地位.显然,第二种场分布对应的增益谱主要特征与双芯光纤非对称平面波增益谱的主要特征完全不同.
图5描述了β2=0.02 ps2/m,γ=5(kW·m)−1,P=400 kW,C1=0时,MI增益谱随线性耦合系数C的演化.可以发现MI带随着C的增加而不断增强,这与双芯光纤中线性耦合系数的影响类似.

图4 参数β2=0.02 ps2/m,γ =5(kW·m)−1,C=200 m−1,C1=0时,正常色散区MI增益谱随总功率P变化的三维图(a)和二维图(b)Fig.4.(a)3D and(b)2D plots showing the variation of the MI gain spectrum with the total power in the normal dispersion regime with β2=0.02 ps2/m,γ =5(kW·m)−1,C=200 m−1,C1=0.
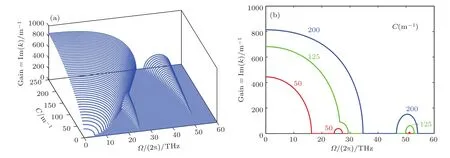
图5 参数β2=0.02 ps2/m,γ=5(kW·m)−1,P=400 kW,C1=0 ps/m时,正常色散区MI增益谱随耦合系数C变化的三维图(a)和二维图(b)Fig.5.(a)3D and(b)2D plots showing the variation of the MI gain spectrum with the coupling coefficient C in the normal dispersion regime with β2=0.02 ps2/m,γ =5(kW·m)−1,P=400 kW,C1=0 ps/m.

图6 参数β2=0.02 ps2/m,γ=5(kW·m)−1,P=400 kW,C=200 m−1时,正常色散区MI增益谱随耦合系数色散C1变化的三维图(a)和二维图(b)Fig.6.(a)3D and(b)2D plots showing the variation of the MI gain spectrum with the coupling coefficient dispersion C1in the normal dispersion regime with β2=0.02 ps2/m,γ =5(kW·m)−1,P=400 kW,C=200 m−1.
图6描述了β2=0.02 ps2/m,γ=5(kW·m)−1,P=400 kW,C=200 m−1时MI增益谱随耦合系数色散C1的变化.低频MI带几乎不受耦合系数色散C1的影响,高频MI带先减弱,然后消失,再重现,并且逐步增强并趋于饱和.我们尝试了不同大小的入射功率,发现高频MI带增益总是很小,低频MI带始终处于主导地位,故三芯光纤中耦合系数色散对增益谱的影响非常小,而在双芯光纤中,在耦合系数色散影响下出现的高频MI带增益可大于低频MI带增益.
3.2.2 反常色散区
考虑参数C=200 m−1,γ=2.5(kW·m)−1,最小入射总功率Pmin=316 kW.
图7描述了β2=−0.02 ps2/m,γ=2.5(kW·m)−1,C=200 m−1,C1=0时,MI增益谱随总功率P的演化.MI带随P的增加而增强,在无扰动条件时对应的MI增益不为零,而在双芯光纤非对称平面波增益谱中,零扰动频率对应的增益为零.
图8描述了β2=−0.02 ps2/m,γ=2.5(kW·m)−1,P=400 kW,C1=0时,MI增益谱随线性耦合系数C的演化,MI带随C的增加而逐渐减弱,其中零扰动频率附近增益先增大后减小,这与双芯光纤非对称平面波增益谱中线性耦合系数的影响基本类似.
图9描述了β2=−0.02 ps2/m,γ=2.5(kW·m)−1,P=400 kW,C=200 m−1时,MI增益谱随耦合系数色散C1的变化.耦合系数色散C1几乎不影响低频MI带,其主要影响是产生一个高频MI带,但是该高频MI带增益非常小.我们尝试了不同大小的入射功率,低频MI带则始终处于主导地位.因此,耦合系数色散C1的影响非常小,而其对双芯光纤增益谱的影响则非常显著.
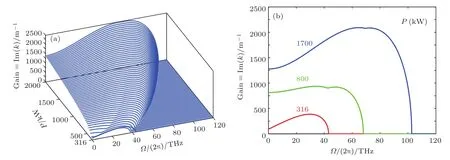
图7 参数β2=− 0.02 ps2/m,γ=2.5(kW·m)−1,C=200 m−1,C1=0时,反常色散区MI增益谱随总功率P变化的三维图(a)和二维图(b)Fig.7.(a)3D and(b)2D plots showing the variation of the MI gain spectrum with the total power in the anomalous dispersion regime for β2= − 0.02 ps2/m,γ =2.5(kW·m)−1,C=200 m−1,C1=0.

图8 参数β2=− 0.02 ps2/m,γ=2.5(kW·m)−1,P=400 kW,C1=0 ps/m时,反常色散区MI增益谱随耦合系数C变化的三维图(a)和二维图(b)Fig.8.(a)3D and(b)2D plots showing the variation of the MI gain spectrum with the coupling coefficient C in the anomalous dispersion regime with β2= − 0.02 ps2/m,γ =2.5(kW·m)−1,P=400 kW,C1=0 ps/m.
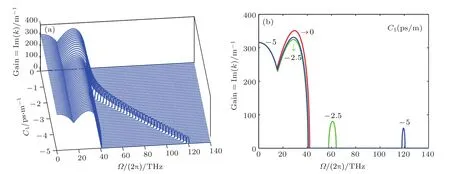
图9 参数β2=− 0.02 ps2/m,γ=2.5(kW·m)−1,P=400 kW,C=200 m−1时,反常色散区MI增益谱随耦合系数色散C1变化的三维图(a)和二维图(b)Fig.9.(a)3D and(b)2D plots showing the variation of the MI gain spectrum with coupling coefficient dispersion C1in the anomalous dispersion regime with β2= − 0.02 ps2/m,γ =2.5(kW·m)−1,P=400 kW,C=200 m−1.
4 结 论
正三角型三芯光纤中等腰对称平面波有两种不同的场分布,第一种场分布即如图1的芯1中场随总功率增强而越来越强,芯2、芯3中场越来越弱;第二种场分布即如图1的芯2和芯3中场随总功率增强而越来越强,芯1中场越来越弱,芯2、芯3中场越来越强.本文首先详细地分析了正三角型三芯光纤等腰对称平面波两种场分布的特点,其次系统研究了它在两种场分布下调制不稳定性增益谱的主要特征,其中第一种场分布对应的调制不稳定性增益谱主要特征与双芯光纤非对称平面波的增益谱相似[35,43],而第二种场分布对应的调制不稳定性增益谱的主要特征与双芯光纤非对称平面波增益谱的主要特征有很大不同.
无扰动时,第二种场分布在正常和反常色散区域均可产生不稳定性增益,且在正常色散区域,无扰动情况对应的增益最强,而在双芯光纤非对称平面波增益谱中,零扰动频率对应的MI增益为零[35].
线性耦合系数在正常色散区域会增强增益谱的增益,在反常色散区域会减弱增益谱的增益,这与其在双芯光纤中的影响相似,而耦合系数色散在正常和反常色散区域对三芯光纤等腰对称平面波的MI增益谱影响均非常弱,这与其在双芯光纤中的影响完全不同.
[1]Alves E O,Cardoso W B,Avelar A T 2016JOSA B33 1134
[2]Copie F,Conforti M,Kudlinski A,Trillo S,Mussot A 2017Opt.Express25 11283
[3]Armaroli A,Biancalana F 2014Opt.Lett.39 4804
[4]Benjamin T B,Feir J E 1967J.Fluid Mech.27 417
[5]Fang Y,Yakimenko V E,Babzien M,Fedurin M,Kusche K P,Malone R,Vieira J,Mori W B,Muggli P 2014Phys.Rev.Lett.112 045001
[6]Mithun T,Porsezian K 2012Phys.Rev.A85 013616
[7]Zhong X,Cheng K,Chiang K S 2014JOSA B31 1484
[8]Canabarro A,Santos B,de Lima Bernardo B,Moura A L,Soares W C,de Lima E,Gleria I,Lyra M L 2016Phys.Rev.A93 023834
[9]Kibler B,Amrani F,Morin P,Kudlinski A 2016Phys.Rev.A93 013857
[10]Armaroli A,Trillo S 2014JOSA B31 551
[11]Agrawal G P 1987Phys.Rev.Lett.59 880
[12]Tanemura T,Ozeki Y,Kikuchi K 2004Phys.Rev.Lett.93 163902
[13]Dinda P T,Porsezian K 2010JOSA B27 1143
[14]Bale B G,Boscolo S,Hammani K,Finot C 2011JOSA B28 2059
[15]Finot C,Wabnitz S 2015JOSA B32 892
[16]Tang D Y,Guo J,Song Y F,Li L,Zhao L M,Shen D Y 2014Opt.Fiber Technol.20 610
[17]Kennedy R E,Popov S V,Taylor J R 2006Opt.Lett.31 167
[18]Pan N,Huang P,Huang L G,Lei M,Liu W J 2015Acta Phys.Sin.64 090504(in Chinese)[潘楠,黄平,黄龙刚,雷鸣,刘文军2015物理学报64 090504]
[19]Gu B,Yuan W,Frosz M H,Zhang A P,He S L,Bang O 2012Opt.Lett.37 794
[20]Bendahmane A,Mussotm A,Kudlinski A,Szriftgiser P,Conforti M,Wabnitz S,Trillo S 2015Opt.Express23 30861
[21]Richardson D J,Fini J M,Nelson L E 2013Nature Photon.7 354
[22]Saitoh K,Matsuo S 2016J.Lightwave Technol.34 55
[23]Radosavljevic A,Danicic A,Petrovic J,Maluckov A,Haziewski L 2015JOSA B32 2520
[24]Sillard P,Molin D,Bigot-Astruc M,Amezcua-Correa A,de Jongh K,Achten F 2016J.Lightwave Technol.34 1672
[25]Wang L,Zhu Y J,Qi F H,Li M,Guo R 2015Chaos25 063111
[26]Zhang J H,Wang L,Liu C 2017Proc.R.Soc.A473 20160681
[27]Wang L,Zhang J H,Liu C,Li M,Qi F H 2016Phys.Rev.E93 062217
[28]Cai L Y,Wang X,Wang L,Li M,Liu Y,Shi Y Y 2017Nonlinear Dyn.90 2221
[29]Wang L,Jiang D Y,Qi F H,Shi Y Y,Zhao Y C 2017Commun.Nonlinear Sci.Numer.Simulat.42 502
[30]Wang L,Wang Z Q,Sun W R,Shi Y Y,Li M,Xu M 2017Commun.Nonlinear Sci.Numer.Simulat.47 190[31]Ding W S,Xi L,Liu L H 2008Acta Phys.Sin.57 7705(in Chinese)[丁万山,席崚,柳莲花 2008物理学报 57 7705]
[32]Trillo S,Wabnitz S,Stegeman G I,Wright E M 1989JOSA B6 889
[33]Tasgal R S,Malomed B A 1999Phys.Scr.60 418
[34]Xiang Y J,Wen S C,Dai X Y,Fan D Y 2010Phys.Rev.E82 056605
[35]Li J H,Chiang K S,Chow K W 2011JOSA B28 1693
[36]Li J H,Chiang K S,Malomed B A,Chow K W 2012J.Phys.B45 165404
[37]Ding W,Staines O K,Hobbs G D,Gorbach A V,de Nobriga C,Wadsworth W J,Knight J C,Skryabin D V,Strain M J,Sorel M 2012Opt.Lett.37 668
[38]Tatsing P H,Mohamadou A,Bouri C,Tiofack G L,Kofane T C 2012JOSA B29 3218
[39]Nithyanandan K,Raja R V J,Porsezian K 2013Phys.Rev.A87 043805
[40]Zhang J G,Dai X Y,Zhang L F,Xiang Y J,Li Y F 2015JOSA B32 1
[41]Ali A K S,Porsezian K,Uthayakumar T 2014Phys.Rev.E90 042910
[42]Mohamadou A,Tatsing P H,Tiofack L C G,Tabi C B,Kofane T C 2014J.Mod.Opt.61 1670
[43]Li J H,Zhou H,Chiang K S,Xiao S R 2016JOSA B33 2357
