Baskakov-Durrmeyer算子在Orlicz空间[0,∞)中逼近的等价定理

韩 领 兄

(内蒙古民族大学 数学学院, 内蒙古 通辽 028043)

1 引言与预备知识

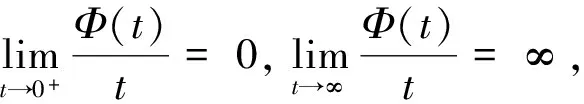
Young函数Φ(t)的互余Young函数记为Ψ(t). 由Young函数Φ(t)的凸性可得Φ(αt)≤αΦ(t),α∈[0,1]. 特别地,Φ(αt)<αΦ(t),α∈(0,1).

定义2[10]设Φ(t)为Young函数. 若存在t0>0和常数C≥1, 使得当t≥t0时, 有Φ(2t)≤CΦ(t), 则称Young函数Φ(t)满足Δ2-条件(记为Φ∈Δ2).

推论1[10]Φ∈Δ2当且仅当对任意的b>1, 存在两个正数α,C, 使得当t≥t0时, 有Φ(bt)≤CbαΦ(t).

定义3[10]设Φ(t)为Young函数. Orlicz类LΦ[0,∞)定义为使有限积分

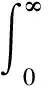
的Orlicz类LΦ[0,∞)的线性包. 其性质如下：

其与Luxemburg范数等价, 即

‖u‖(Φ)≤‖u‖Φ≤2‖u‖(Φ).

(1)

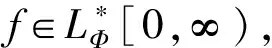
文献[7-8]得到了连续模与K-泛函的等价性.

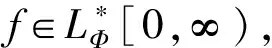
C-1ωr,φ(f,t)Φ≤Kr,φ(f,tr)Φ≤Cωr,φ(f,t)Φ.

(2)

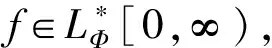
设f(x)为[0,∞)上的可积函数, Baskakov-Durrmeyer算子[1]Vn定义如下:

2 正定理

引理1[6]

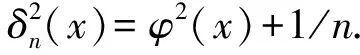
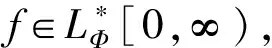
引理3[11]对于φ2(x)=x(1+x), 若u在t与x之间, 则

引理4[12]对于φ2(x)=x(1+x), 若u在t与x之间, 且x∈[0,1/n), 则

引理5设g″∈LΦ[0,∞), 则

证明: 当x∈[1/n,∞)时,δn(x)≤2φ(x), 由引理4得

由式(5)得

再由性质1得

(7)

令

由于

所以

由性质1得

(8)

结合式(7),(8), 得

(9)

又由性质1得

(10)

证毕.

利用文献[7]中引理2.3和文献[13]中引理1可得如下结论:

其中C表示与n和x无关的正常数.

证明: 首先构造一个函数An(f,x)(n≥3), 使得

(11)

从而

(12)

由积分型余项的Taloy公式, 得

由于

因此, 由引理5和引理6, 得

(13)

结合式(4),(11)～(13), 有

证毕.

3 逆定理

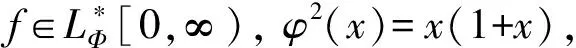
从而

由于‖Ji‖Φ(i=1,2,…,12)的估计类似, 所以只需给出‖J1‖Φ的估计. 由式(1)式和Jensen不等式, 得

其中:vn+1,-2(x)=0;vn+1,-1(x)=0. 从而

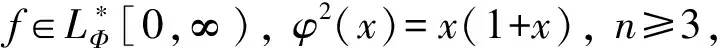
证明: 运用Leibniz定理得

结合式(14),(15), 得

(t)f(t)dt.

用两次分部积分法得

从而

(17)

由式(16),(17)得

由于‖Fi‖Φ(i=1,2,3,4)的估计类似, 所以只需给出‖F1‖Φ的估计. 利用式(1)和Jensen不等式, 得

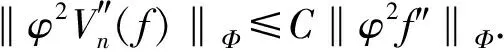
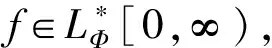
证明:

利用式(1)和Jensen不等式, 得

证明: 通过简单计算可得

利用式(1)和Jensen不等式, 得

1)ω2,φ(f,t)Φ=O(tα/2);

2)ω1(f,t)Φ=O(tα/2).

证明: 1) 由K-泛函的定义, 可选取g(x)=Vn(f,x), 使得

(f)‖Φ.

由‖Vn(f)-f‖Φ=O(n-α/2)及定理4和引理7, 可得

由Berens-Lorentz引理[11]得t=1/n,K2,φ(f,t2)Φ≤Ctα/2, 0≤α<2. 再由式(2)得ω2,φ(f,t)Φ=O(tα/2).

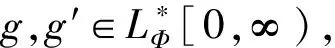
由K-泛函的定义, 对于t=1/n, 选取g使得

另一方面, 利用引理8和引理9, 可得

再运用Berens-Lorentz引理, 得K1(f,t)Φ≤Ctα/2, 0≤α<2. 最后估计ω1(f,t)Φ=O(tα/2). 设

其中

可得

从而

蕴含ω1(f,t)Φ=O(tα/2). 证毕.

由定理3和定理5可得:

‖Vn(f)-f‖Φ=O(n-α/2) ⟺ω2,φ(f,t)Φ=O(tα/2),ω1(f,t)Φ=O(tα/2).

[1] Heilmann M. Direct and Converse Results for Operators of Baskakov-Durrmeyer Type [J]. Approx Theory Appl, 1989, 5(1): 105-127.

[2] 刘喜武, 郭顺生, 宋占杰. Baskakov-Durrmeyer型算子的带权同时逼近 [J]. 吉林大学自然科学学报, 1999(4): 21-24. (LIU Xiwu, GUO Shunsheng, SONG Zhanjie. Weighted Simultaneous Approximation of Baskakov-Durrmeyer Operators [J]. Acta Scientiarum Naturalium Universitatis Jilinensis, 1999(4): 21-24.)

[3] QI Qiulan, GUO Shunsheng. Simultaneous Approximation by Baskakov-Durrmeyer Operator [J]. Chin Quart J of Math, 2001, 16(1): 38-45.

[4] 毛梁成. Baskakov-Durrmeyer算子同时逼近 [J]. 宝鸡文理学院学报(自然科学版), 2007, 27(2): 103-106. (MAO Liangcheng. Simultaneous Approximation by Baskakov-Durrmeyer Operators [J]. Journal of Baoji University of Arts and Sciences (Natural Science Edition), 2007, 27(2): 103-106.)

[5] 郭顺生, 宋占杰. Baskakov-Durrmeyer算子的点态逼近 [J]. 数学研究与评论, 2001, 21(3): 441-446. (GUO Shunsheng, SONG Zhanjie.Pointwise Approximation by Baskakov-Durrmeyer Operator [J]. Journal of Mathematical Research and Exposition, 2001, 21(3): 441-446.)

[6] 杨戈, 石宁, 徐爱华. 关于Baskakov-Durrmeyer算子的强逆逼近 [J]. 河北工程大学学报(自然科学版), 2007, 24(1): 110-112. (YANG Ge, SHI Ning, XU Aihua. Strong Converse Approximation for Baskakov-Durrmeyer Operators [J]. Journal of Hebei University of Engineering (Natural Science Edition), 2007, 24(1): 110-112.)

[7] 韩领兄, 吴嘎日迪, 刘国锋. Orlicz空间中加权光滑模与K-泛函的等价性及其应用 [J]. 数学物理学报, 2014, 34A(1): 95-108. (HAN Lingxiong, WU Garidi, LIU Guofeng. The Equivalence of the Smooth Modulus with Weights and aK-Functional in Orlicz Spaces and Its Application [J]. Acta Mathematica Scientia, 2014, 34A(1): 95-108.)

[8] HAN Lingxiong, WU Garidi. Approximation by Modified Summation Integral Type Operators in Orlicz Spaces [J]. Applied Mathematics, 2017, 30(3): 613-622.

[10] HE Yuzan. Ba Spaces and Orlicz Spaces [J]. Function Spaces and Complex Analysis, 1997, 2: 37-62.

[11] Ditzian Z, Totik V. Moduli of Smoothness [M]. New York: Springer-Verlag, 1987.

[12] QI Qiulan, GUO Shunsheng, LI Jiankun. Approximation by Modified Summation Integral Type Operators in theLpSpaces [J]. Journal of Mathematical Research and Exposition, 2009, 29(6): 1069-1081.

[13] Ditzian Z, Totik V.K-Functionals and Weighted Moduli of Smoothness [J]. J Approx Theory, 1990, 63(1): 3-29.