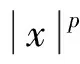带有无限时滞随机发展方程的Khasminskii-型定理

蔡志丹, 刘青青, 吕显瑞

(1. 长春理工大学 理学院, 长春 130022; 2. 洛阳师范学院 数理学院, 河南 洛阳 471934; 3. 吉林大学 数学学院, 长春 130012)

0 引 言

为使一个随机微分方程对任意给定的初始值都有唯一的全局解, 方程的系数通常需要满足线性增长条件和局部Lipschitz条件[1-2], 或者满足一个给定的非Lipschitz条件和线性增长条件[3-4], 即线性增长条件在抑制解的潜在爆炸和保证解的存在性方面具有重要作用. 文献[5-6]将上述两类情形推广到了无穷时滞随机泛函微分方程上. 但实际应用中, 许多重要的无穷时滞系统并不满足线性增长条件, 因此, 研究这些系统解的全局存在性具有一定的应用价值.

经典的Khasminskii-型定理在没有线性增长条件的情形下, 通过使用Lyapunov函数研究了随机微分方程解的全局存在性[7-12], 进而对有限随机微分方程的全局解建立了各种存在唯一性定理. 文献[13]给出了不满足线性增长条件的无穷时滞随机泛函方程解的存在唯一性定理. 但对于带有无穷时滞的随机发展方程, 目前尚未见文献报道. 本文考虑带无限时滞的随机发展方程

dx(t)=(Ax(t)+f(t,xt))dt+g(t,xt)dWt,

(1)

其中:xt=xt(θ)∶={x(t+θ): -∞<θ≤0};A表示从V到V*的有界线性算子;f:+×BC((-∞,0];H)→H和g:+×BC((-∞,0];H)→L(U,H)是Borel可测的,H,U表示可分的Hilbert空间, 有一个数量积〈·,·〉.V是一个可分的Banach空间, 其范数为 ‖·‖,V⊂H是连续稠密的,V*是V的对偶空间. 由Riesz同构知,V⊂H=H*⊂V*是连续稠密的.BC((-∞,0];H)表示从(-∞,0]到H, 具有范数<∞, 构成一个Banach空间的有界连续函数族.L(U,H)表示所有从U到H的有界线性算子空间,L(U,H)是Banach空间,W是(Ω,F,P)上U-值的Brown运动. 令(Ω,F,P)是一个带有信息流{Ft}t≥0的完备概率空间,C2(H,+)是H上所有连续两次可微的非负函数族, 对任意的V ∈C2(H,+), 定义LV为

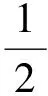
假设:

(H1) 设A是一个从V到V*上的有界线性算子, 对p≥2, 存在一个常数δ, 使得对μ∈V, 有‖Aμ‖*≤δ‖μ‖p-1, 且满足下述强制性条件: 存在常数α>0和γ>0, 使得

(H2)f和g满足局部的Lipstiz条件,φ,φ∈BC((-∞,0];H),t≥0, 对每个k>0, 存在一个常数ck, 使得

‖f(t,φ)-g(t,φ)‖H∨‖g(t,φ)-g(t,φ)‖H≤ck‖φ-φ‖H,

其中‖φ‖H,‖φ‖H≤k.

1 主要结果

对方程(1)应用标准的截断技术, 可得:

定理1在假设条件(H1),(H2)下, 对任意的初值ξ∈BC((-∞,0];H), 方程(1)在-∞

则方程(1)在[0,+∞]上存在一个概率1意义下的全局解.

证明： 由假设(H1),(H2)和定理1知, 对任意的初值ξ∈BC((-∞,0];H), 方程(1)在t∈(-∞,τe)上都有一个唯一的局部强解x(t), 其中τe表示爆破时间. 为了证明该解是全局的, 只需证明τe=∞. 注意到ξ∈BC((-∞,0];H), 因此必存在一个正数k0, 使得|ξ(0)|≤k0. 对每个整数k>k0, 定义停时

τk=inf{t∈[0,τe]: |x(t)|≥k}.

显然τk是递增的, 并且当k→∞时,τk→τ∞≤τe. 若τ∞→∞, 则τe=∞, 即x(t)是一个全局解. 其等价于对任意的t>0, 当k→∞时,P(τk≤t)→0. 由条件(2), 对V (x(t)), 应用It公式可得

利用Fubini定理, 可得如下估计：

类似地, 有

(5)

注意到K(t)是一个不减的函数, 将式(4),(5)替换到式(3)中得

(6)

利用Gronwall不等式, 有

其中:

由停时τk的定义, 有

即当k→∞时,P(τk≤t)→0. 证毕.

为了使条件更简便, 指定条件(2), 对任意的φ∈BC((-∞,0];H), 对f,g应用如下条件.

定理3假设(H1),(H2)成立, 在条件1),2)下, 如果

(7)

由假设(H2), 有

由条件1), 有

由条件2)应用Hölder不等式得

由I0,I1,I2得

其中

注意到α>2β,p≥2, 因此有

其中K(t)=H(x),a=1,b=c=0. 应用定理2即可得到结果. 证毕.

[1] Arnold L. Stochastic Differential Equations: Theory and Applications [M]. New York: Wiley, 1974.

[2] MAO Xuerong. Stochastic Differential Equations and Applications [M]. Chichester: Horwood Publishing Limited, 1997.

[3] FANG Shizan, ZHANG Tusheng. A Study of a Class of Stochastic Differential Equations with Non-Lipschitzian Coefficients [J]. Probab Theory Related Fields, 2005, 132(3): 356-390.

[4] MAO Xuerong. Exponential Stability of Stochastic Differential Equations [M]. New York: Marcel Dekker Inc, 1994.

[5] REN Yong, XIA Ningmao. Existence, Uniqueness and Stability of the Solutions to Neutral Stochastic Functional Differential Equations with Infinite Delay [J]. Appl Math Comput, 2009, 210(1): 72-79.

[6] WEI Fengying, WANG Ke. The Existence and Uniqueness of the Solution for Stochastic Functional Differential Equations with Infinite Delay [J]. J Math Anal Appl, 2007, 331(1): 516-531.

[7] Khasminskii R Z. Stochastic Stability of Differential Equations [M]. Alphen Aanden Rijn: Sijthoff and Noordhoff, 1980.

[8] MAO Xuerong, Rassias M J. Khasminskii-Type Theorems for Stochastic Differential Delay Equations [J]. Stoch Anal Appl, 2005, 23(5): 1045-1069.

[9] SHEN Yi, LUO Qi, MAO Xuerong. The Improved LaSalle-Type Theorems for Stochastic Functional Differential Equations [J]. J Math Anal Appl, 2006, 318(1): 134-154.

[10] WU Fuke. Khasminskii-Type Theorems for Neutral Stochastic Functional Differential Equations [J]. Math Appl, 2008, 21(4): 794-799.

[11] LI Xinpeng, LIN Xiangyun, LIN Yiqing. Lyapunov-Type Conditions and Stochastic Differential Equations Driven byG-Brownian Motion [J]. J Math Anal Appl, 2016, 439(1): 235-255.

[12] XING Jiaming, LI Yong. Explosive Solutions for Stochastic Differential Equations Driven by Lévy Processes [J]. J Math Anal Appl, 2017, 454(1): 94-105.

[13] WU Fuke, HU Shigeng. Khasminskii-Type Theorems for Stochastic Functional Differential Equations with Infinite Delay [J]. Statist Probab Lett, 2011, 81(11): 1690-1694.