一种教学用六轴工业机器人的研制

彭建新，黄伟朝

（肇庆市技师学院，广东 肇庆 526060）

六轴工业机器人在工业生产中应用最广泛，技工院校教学中也采用最多。由于厂家机器人的价格较高，实训教学中数量有限。为增加机器人的实训台位，需要开发一种具有一定替代性的六轴工业机器人。

1 机器人本体的设计

本文设计了一种负载0.5kg的六轴机器人本体，其机械结构采用工业中广泛应用的通用六轴工业机器人结构，如图1。

（1）机器人本体设计主要包括传动系统、电机选型和减速器的选型设计。本机器人本体采用六轴串联关节式结构型式。

为简化结构，机器人的6个关节均采用步进电机和减速器相结合的机械结构。如表1是各关节电机及减速器的型号、参数。

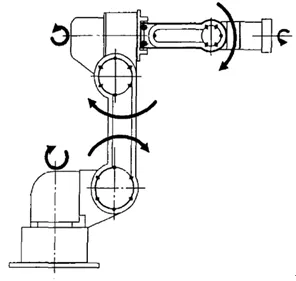
图1 六轴工业机器人结构

该机器人的主要性能指标有：本体重量：10g，最大回转半径 ：646mm；负载能力：0.5g；末端定位精度：2mm。既可在PC机界面上操控，也可用手轮操作，PC机示教再现。

表1 电机与减速器的型号与参数

（2）步进电机选型的计算。电机保持力矩必须大于静态负载扭矩；惯量匹配，即使负载等效惯量不超过电机转子惯量的12倍；电机保持力矩减去静态负载扭矩的差值必须足够大。以上3点是选型步进电机应该满足的要求。下面以第二轴步进电机为例，说明选型过程。

首先，计算静态负载扭矩。当大臂和小臂呈直线且水平，手臂端点负载0.5kg，此种情况将产生最大的静态负载扭矩。用Pro/E软件的质量计算和重心测量的功能，测量大小臂加负载的总重量M是2.5kg，等效重心到第一轴的距离L是384mm。

静态负载扭矩T：T=M×g×L。

将负载重量和距离代入上式，计算得到静态负载扭矩：

T=2.5×9.8×0.384=9.6N·m。

已知减速器减速比i为45，则等效到电机轴的负载：Tz=T/i。

将负载重量和距离代入上式，计算得：Tz=9.6/45=0.213N·m。可见电机的最大静态扭矩必须大于0.213N·m。

其次，计算等效转动惯量。已知减速器减速比i为45，等效转动惯量：

Jd=Jm/i2=M×L2/i2

将重量和长度代入上式，计算得：

Jd=2.5×3842/452=182.04 kg·mm2。

根据惯量匹配原则，要求电机的转动惯量：

Jm＞ Jd/12=182.04/12=15.17 kg·mm2。

再次，初步选取电机。电机的最大静态转矩Tsm必须大于0.213N·m，且转动惯量大于15.17 kg·mm2。57BYG76-2.8A电机的最大静态转矩1.89N·m，转动惯量为48kg·mm2，满足上述2个要求，且有一定余量。

（3）减速器选型计算。最大静态转矩和运动精度是减速器选型的主要依据。本文设计的机器人对重复定位的精度要求小于2mm，等效转换到减速器的回程间隙是4弧分，为简化结构，采用自制涡轮蜗杆减速器。减速器的极限扭矩大于所传递的极限扭矩。本机器人所用减速器按上述要求选择，如表1所示。

（4）同步带选型计算。本文所设计的机器人的第一轴采用了同步带传动，已知所要传递的额定扭矩等于步进电机的保持扭矩1.89N·m。先选择带型XL梯形同步带，再选择皮带宽度5mm，皮带长200，选定皮带轮的齿数20。如果不满足要求，可以调整皮带宽度、带轮齿数、带型参数，然后计算校核，这样循环反复，最终找到合适的目标。

2 运动控制器的选择

本文所研制的机器人采用现成的nMotion-v5.0运动控制卡。该卡支持Mach3所有的版本，使用USB接口，无需驱动，支持热插。USB总线采用高档芯片磁耦隔离，是真正有价值的隔离。双核超高速CPU（单核最高主频204MHz）。6轴联动的脉冲输出频率最高达300kHz，可接伺服/步进电机。拥有16路隔离输入口，输入接口更简单，端口干湿接点均可。带有256字节NVRAM空间，可保存6个轴的座标值，下次上电无需找零点。

该运动控制卡的接线框图见图2。PC机通过USB接口与运动控制卡通讯，可完成运动规划、高速实时插补、伺服滤波控制和伺服控制，同时随控制器还提供功能强大的运动控制软件库，可供用户根据不同的需要开发应用软件，组成各种控制系统。

3 机器人控制系统

机器人控制系统用于对机器人的控制，以完成特定的工作任务。由于采用nMotion-v5.0运动控制卡，所以上位机控制系统采用Mach3 Mill程序。上位机选取通用PC机，以较低的成本组成较强性能的系统，而且还方便进行二次开发。

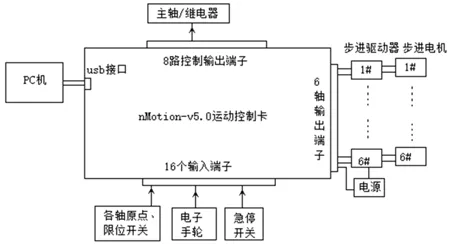
图2 nMotion-V5.0运动控制卡接线框图

（1）关于运动学逆解。Mach3 Mill是控制铣床的机床控制系统，最多可控制3个旋转、3个移动共6个自由度的运动，如用来控制六轴工业机器人的动作，必须进行空间坐标转换，即将目标点的空间坐标转换成6个轴的转动角度。为此，要进行运动学求解和逆解。

首先，建立一个固定的空间坐标系，然后通过坐标参数描述物体在该参考坐标系中的位置和姿态（简称位姿）。利用位姿矩阵实现不同坐标系中的空间坐标变换。设空间一点P在坐标系{A}和{B}中的齐次坐标分别为AP=(APX,APY,APZ,1)T和BP=(BPX,BPY,BPZ,1)T；则有关系式：AP=BAT.BP，其中BAT是坐标系B到坐标系A的变换矩阵。

工业机器人的旋转关节一般分成2种：转轴平行于连杆的（P型）和转轴垂直于连杆的（V型），见图3。1个关节单元由互相垂直的P型和V型关节连接而成。单元i的P型关节记为Pi，轴线方向（指向V型关节的方向）记为Pi；V型关节记为Vi，轴线方向记为Vi。

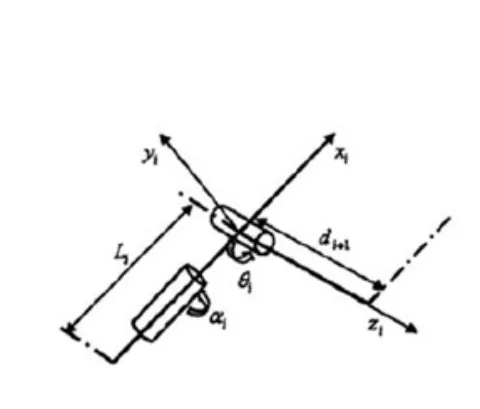
图3 关节单元模型

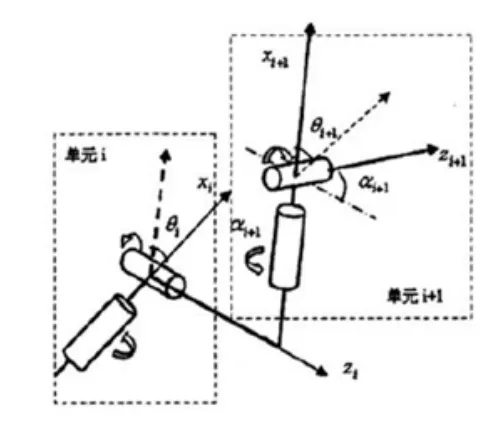
图4 相邻关节单元的关系

如图4，从关节单元i的坐标系到关节单元i+1的坐标系变换如下。

①绕着zi轴逆时针旋转θi，使得xi轴和xi+1轴平行。

②沿着zi轴平移di，使得xi轴和xi+1共线。

③沿着xi+1平移Li+1，使得zi轴和zi+1共面。

④绕着xi+1轴逆时针旋转аi+1，使得zi轴和zi+1共线。

因此，变换矩阵为：

i+1iT=Rot(z,θi)·trans(0,0,di)·trans(Li+1,0,0)·Rot(x,аi+1)

其中Rot(z,θi)是绕z轴旋转θi的旋转矩阵，trans(0,0,di)是在z轴平移di的平移矩阵，其它矩阵均类似。

经过整理，最后得到变换矩阵是：

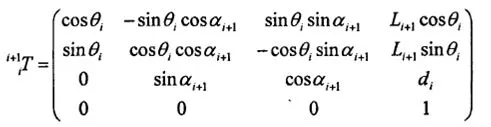
机械臂运动学方程就是要建立机械臂末端坐标系{n}关于基坐标系{0}的变换方程，只需将n个关节的变换矩阵依次相乘即可。

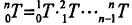
本文机器人有6个自由度，可以灵活地在三维空间中运动。该机械臂系统由4个关节单元连接而成，各个关节单元的参数见表2。

表2 机械臂结构参数

求解运动学方程也就是所谓机械臂的运动学逆问题，已知末端位置EG(或末端位姿EAT)，求а1，θ1，а2， …а4。 设 P=(0，0，0，1)T， 则 有关系式 EG=EAT.P，求解方程：BAT(а1).CBT(θ1).DCT(θ2,а3).EDT(θ3,а4)=EG 则可得到各关节角度а1，θ1，а2，…а4。求解的方法有很多，限于篇幅这里不赘述。

（2）关于控制系统有关参数设置。①电机单位当量脉冲数。本机器人使用是二相步进电机，单位脉冲当量=200×驱动器细分数×减速比/丝杆导程（螺距），如驱动器细分数=16，丝杆导程=4mm，减速比=45，则单位当量=200×16×45/4=36000。对于转动，则角度脉冲当量=200×16×45/360=400，即每400脉冲转过1°。②Mach3中输入信号的配置。本运动卡的输入信号编号从1到16，在Mach3中配置为低电平有效，端口号（Port Number）为2。

（3）爪手的控制。利用运动控制卡对主轴电机的控制功能来控制爪手的动作。用对主轴电机驱动的PWM信号来控制舵机，用舵机来直接控制爪手。一般脉宽在1～2ms，所以PWM信号频率500～1kHz。用主轴继电器通断（M3M5）控制舵机信号的通断。

4 效果

该六轴机器人相对于企业成熟的机器人，具有以下优势：价格低廉，能配备较多的实训工位；便于学生观察机器人的结构，深入体会其工作原理。

便于学生直接参与机器人的装配，通过对各关节机械传动的理解，为机器人的维修保养课程打基础；开源软件能让学生深入理解、编写控制程序；取材容易，结构简单，易于操作，性能稳定，安全可靠。当然，与企业成熟的机器人相比，它的功能相对简单。

[1]仲晓帆.基于CODESYS 的六关节机器人运动控制方法研究[D].浙江工业大学，2015.

[2]范叔炬.机械臂运动学算法设计[D].浙江大学，2008.

[3]王才东.六自由度教学机器人控制系统设计及实验研究[D].哈尔滨工业大学，2008.

[4]张涛.机器人引论[M].机械工业出版社，2010.

[5]黄政杰.六自由度FOXBOT机械手臂动力学之探讨[D].国立勤益科技大学，2011.