冲击荷载下CRTSⅡ型板式无砟轨道结构振动与噪声的关联性研究
2018-03-27王启好崔日新田秋实
王启好,崔日新,肖 宏,田秋实,王 冠
(北京交通大学轨道工程北京市重点实验室,北京 100044)
高速铁路及城市轨道交通的快速发展不仅能有效改善交通环境,而且还有助于带动城乡建设和经济发展,具有显著的经济和社会效益,但其运行中所产生的振动与噪声问题也不容忽视,过度的振动噪声不仅严重影响乘客和沿线人们的正常生活,还可能引起有关设备和结构以及周边建筑物的疲劳损坏,缩短使用寿命[1],因此解决此方面的问题也成为了铁路修建运营的重要一部分。
国内外针对振动和噪声已有大量的研究,如D.J.Thompson研究了频率在250~5 000 Hz的轮轨噪声,并与实测结果进行了比较,结果认为在整个频带内轨道噪声高于车轮,而车轮噪声在1 000 Hz以上频率占主要成分[2];张筱茜通过有限元法讨论了由高速铁路列车运行引发的环境振动的动态特性[3];尹皓、李耀增和辜小安等通过对高速铁路运行时不同区段测试,进行噪声频谱特性分析[4]。
从上述的国内外对轨道结构振动与噪声的研究可以看出,目前的研究主要针对振动[5]或者噪声[6]各自的研究较多,对二者之间的内在联系研究尚未开展。基于此,主要设计足尺模型试验,系统研究冲击荷载[7]作用下CRTSⅡ型板式无砟轨道[8]结构振动与噪声特性以及其内在的关联性[9],为轨道结构减振[10]降噪[11]设计奠定基础。
1 试验概况
模型试验采用轨道结构为足尺的CRTSⅡ型板式无砟轨道,如图1所示。由于本次试验涉及测定钢轨噪声相关特性,为避免周围环境噪声干扰,试验在凌晨1点左右进行。

图1 模型试验现场
2 测试内容与元件布置
根据研究需要,主要进行钢轨、轨道板、底座板等不同位置处的加速度、声强、声压等指标测试。参考国外钢轨噪声计算模型[12]后,布置的传感器位置如表1和图2所示。

表1 测点及传感器描述

图2 测点位置布置
3 试验方法及工况
试验装置由加载系统、足尺模型、数据采集系统、数据处理系统组成。参考文献[13],冲击荷载采用力锤加载,即将不同方向的荷载加载在不同位置的钢轨上,以此模拟列车运行时车轮对钢轨的作用,其中侧向冲击荷载模拟直线和曲线地段列车运行时车轮对钢轨的侧向冲击,垂向冲击荷载模拟钢轨表面不平顺和接头处对钢轨的垂向冲击。利用DASP软件系统[14]收集无砟轨道钢轨轨顶、轨腰、轨底等位置的加速度、声压及声强。试验工况见图3。

图3 试验工况
4 试验的结果分析
4.1 振动分析
4.1.1 钢轨跨中位置侧向锤击
在跨中轨顶位置进行侧向锤击,测得的加速度时程如图4所示。限于篇幅,仅列出钢轨跨中各位置侧向加速度时程。
从图4看出,加速度衰减快,在20~30 ms内已衰减完。从轨顶到轨腰再到轨底,峰值逐渐减小。
为了进行频域对比分析,将测试的加速度时程图进行快速傅里叶变换(FFT)得到振动加速度谱[15],如图5所示。
从图5可以看出,钢轨各位置处加速度峰值的频率、峰值大小均不同。从轨顶到轨腰再到轨底,侧向加速度明显减弱,垂向加速度明显增强,纵向加速度一直不明显;侧向加速度峰值一直在1 400~2 100 Hz频率区间内,垂向加速度在轨腰处峰值在2 100 Hz频率附近,轨底处峰值在1 600 Hz频率附近。

图4 钢轨各位置处侧向加速度时程
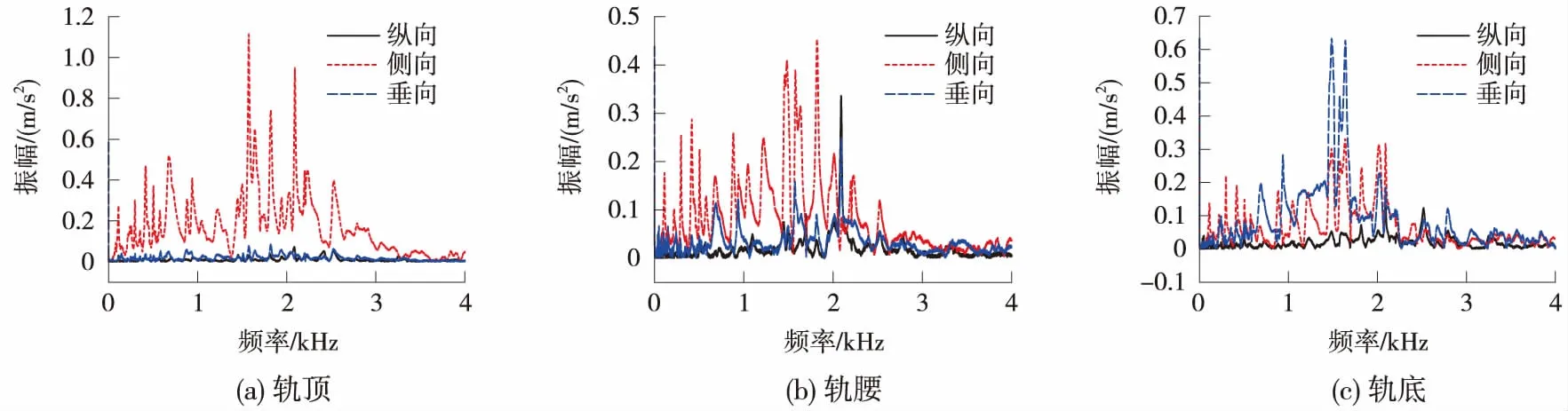
图5 侧向锤击下钢轨各位置处三向加速度频谱
跨中轨顶处以侧向加速度为主,峰值出现在1 600~2 100 Hz频率区段。跨中轨腰位置处以侧向和垂向加速度为主,侧向加速度峰值出现在1 400~1 800 Hz频率区段,垂向加速度峰值出现在2 100 Hz频率附近。跨中轨底位置处垂向加速度明显增大,垂向加速度峰值出现在1 600 Hz频率附近,侧向加速度峰值出现在1 600、2 100 Hz频率附近。
4.1.2 钢轨跨中位置垂向锤击
通过FFT变换获得垂向锤击下钢轨各位置处三向加速度频谱图,如图6所示。

图6 垂向锤击下钢轨各位置处三向加速度频谱
从图6可以看出,钢轨各位置处加速度峰值的频率、峰值大小均不同。侧向加速度从轨顶到轨腰再到轨底逐渐减弱,垂向加速度逐渐增强,纵向加速度一直不明显;侧向加速度峰值一直在1 400~1 600 Hz频率区间内,垂向加速度峰值分布范围广。
跨中轨顶、轨腰、轨底处均以垂向、侧向加速度为主。跨中轨顶侧向加速度峰值出现在1 600 Hz频率附近,垂向加速度峰值在300~2 100 Hz均有分布。跨中轨腰位置处侧向加速度峰值出现在1 400 Hz频率附近,垂向加速度峰值在300~2 400 Hz均有分布。跨中轨底位置处垂向加速度明显增大,侧向加速度峰值出现在1 500、3 500 Hz频率附近,垂向加速度峰值在300~2 400 Hz、3 500 Hz附近均有分布,最大峰值出现在1 600、2 100 Hz频率附近。
同时在上述几种情况下,对比轨道板和底座板加速度时,均发现了相同的传递规律[16],从钢轨到道床(板)逐层衰减,如图7所示。

图7 底座板与轨道板加速度频谱对比
从图7看出,轨道板和底座板加速度频谱峰值凸出明显,频谱图形式简单。轨道板加速度峰值出现在500 Hz频率处,底座板峰值出现在2 000 Hz频率处。
4.2 噪声分析
4.2.1 钢轨跨中位置侧向锤击
在跨中轨顶位置进行侧向锤击,测得的跨中轨顶、轨腰声强时程如图8所示。

图8 钢轨跨中各位置声强时程
从图8看出,声强衰减较快,在20~30 ms内已衰减完成。从轨顶到轨腰,峰值变大。
为了进行频域对比分析,将测试的声强时程进行快速傅里叶变换(FFT)得到频谱图,如图9所示。
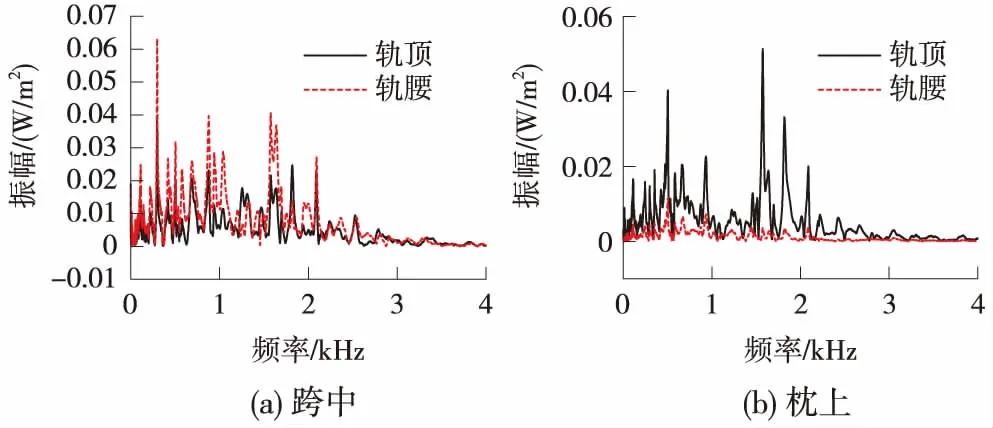
图9 钢轨各位置处声强频谱
从图9可以看出,钢轨跨中位置,轨腰处声强峰值比轨顶处大。跨中轨顶、轨腰处峰值出现在400、1 000、1 600 Hz附近。枕上轨顶处声强远大于轨腰处声强。枕上轨顶处声强峰值出现在500、1 500 Hz附近。
4.2.2 钢轨跨中位置垂向锤击
通过FFT变换获得跨中垂向锤击下钢轨各位置处声强频谱,如图10所示。

图10 垂向锤击下钢轨各位置处声强频谱
从图10可以看出,钢轨跨中位置,轨腰声强峰值比轨顶大。轨顶处峰值出现在500、900、1 700 Hz附近。轨腰处峰值出现在900、1 700 Hz附近。枕上位置,轨顶处声强峰值远大于轨腰处。轨顶处峰值出现在800、1 400、2 000 Hz频率附近。
4.3 关联性分析
4.3.1 钢轨跨中位置侧向锤击
将钢轨跨中各位置处的加速度和声强频谱图进行对比[18],如图11所示。

图11 侧向锤击下加速度与声强对比
从图11发现,声强和侧向加速度峰值的出现有很强的相似性,在侧向加速度出现峰值时,相应频段的声强也会出现峰值。分析多组数据后,发现这种规律并不是偶然的。在跨中轨顶位置处,侧向加速度和声强在0~2 200 Hz频段峰值吻合良好;在跨中轨腰位置处,侧向加速度和声强在0~1 200 Hz频段峰值吻合良好。
4.3.2 钢轨跨中位置垂向锤击
将钢轨跨中各位置处的加速度和声强频谱图进行对比,如图12所示。

图12 垂向锤击下加速度与声强对比
从图12发现,在垂向激励作用下,跨中轨顶位置处钢轨的振动响应相比侧向激励时复杂,侧向和垂向加速度均较大,垂向加速度对0~2 000 Hz频段声强影响大,侧向加速度对声强的贡献不明显。跨中轨腰位置处,在0~1 500 Hz频率区段内,声强主要受垂向加速度影响,与侧向加速度的关联小。
5 结论
(1)在钢轨跨中位置分别施加侧向和垂向激励,钢轨均产生侧向振动和垂向振动,从轨顶到轨腰再到轨底,侧向振动逐渐减弱,垂向振动逐渐增强。
(2)声强主要与钢轨振动有关,钢轨跨中位置轨顶处声强频谱峰值比轨腰处小,而枕上位置轨顶声强频谱峰值比轨腰大。
(3)侧向激励下,轨顶和轨腰位置声强主要受侧向振动影响。垂向激励下,钢轨各位置声强频率0~1 500 Hz区段主要受垂向振动影响,侧向振动幅度虽然大,但对声强贡献不明显,仅能看出对1 700 Hz频率处声强产生明显影响。
(4)振动与噪声关联最强情况为跨中侧向激励下跨中轨顶位置处,声强与侧向加速度频谱峰值的出现基本达到一一对应关系。
[1] 宋传江.高速铁路和城市轨道线路橡胶减震制品的现状和发展[J].橡胶科技市场,2009(6):1-6.
[2] Thompson D J. Prediction of the acoustic radiation from vibrating wheels and rails[J]. Journal of Sound and Vibration, 1988,120(2):275-280.
[3] 张筱茜.高速铁路环境振动动态特性分析[D].成都:西南交通大学,2015.
[4] 尹皓,李耀增,辜小安.高速铁路列车运行噪声特性研究[J].铁道劳动安全卫生与环保,2009(5):221-224.
[5] Hugh S, James P. In-service tests of the effectiveness of vibration control measures on the BART rail transit system[J]. Journal of Sound and Vibration, 2006,293(3-5):888-900.
[6] Donald Te,Marco S,Joe K. Railway noise and the effect of top of rail liquid friction modifiers: changes in sound and vibration spectral distributions in curves[J]. Wear, 2004,258(7-8):1148-1155.
[7] 练松良,刘富.轨道刚度变化对轮轨冲击荷载的动力影响[J].同济大学学报(自然科学版),2002(4):427-430.
[8] 吴斌,陈文荣,刘参,等.列车竖向荷载下CRTSⅡ型板式无砟轨道结构受力特性试验研究[J].铁道科学与工程学报,2014(3):37-42.
[9] 刘震,刘林芽.无砟轨道钢轨导纳特性的实验研究[J].噪声与振动控制,2012(3):78-81.
[10] 魏民.隔震结构中阻尼对隔震效果的影响[D].济南:山东大学,2011.
[11] 谷爱军,张宏亮,李文会,等.城市轨道交通高架线噪声控制问题分析[J].都市快轨交通,2013(4):6-9.
[12] Janssens M,Thompson D J. A Calculation Model For The Noise From Steel Railway Bridges[J].Journal of Sound and Vibration, 1996,193(1):295-305.
[13] 侯传伦.重载铁路曲线段磨耗状态下轮轨相互作用分析[D].成都:西南交通大学,2009.
[14] 应怀樵,刘进明,沈松.把试验室拎着走——数据采集和信号处理软件DASP2000性能介绍[C]∥中国振动工程学会振动与噪声控制专业委员会,第十五届全国振动与噪声高技术及应用会议论文集:2001年卷,现代振动与噪声技术,2001:219-225.
[15] 刘林芽,雷晓燕.轮轨噪声的预测[J].铁道学报,2004(1):101-104.
[16] 周广庆.地铁常用轨道结构振动传递特性理论和试验分析[D].北京:北京交通大学,2015.
