基于Ansys的某型舰炮托架拓扑优化设计

黄观明，杨宏亮，张建波，刘圣强

(郑州机电工程研究所，河南 郑州 450015)

0 引 言

旋回架是某型舰炮的主要支撑结构，其主要由炮床和2个托架组成。2个托架构成U型大耳轴形式，托架耳环对称安装左、右高低滚珠座圈的外环，两者共同作用在垂直面上转动，保证舰炮装置进行高低瞄准。托架的主要作用是支撑舰炮摇架、自动机和供弹系统的重力，以及承受舰炮射击过程中产生的作用力。舰炮总体对各部件的质量都有严格的要求，因此在方案设计的过程中需要对托架结构进行优化设计，使得在满足结构刚度和强度的条件下，托架质量达到最小，进而减轻旋回架的质量，实现轻量化设计的目的。旋回架的结构如图1所示。

拓扑优化是结构优化设计领域最常用的方法[1]。均匀化法是连续体拓扑优化中应用非常广泛的一种方法，如果结构的模型、材料特性和载荷工况都不是很复杂的情况下，该方法计算时间短，迭代次数小，且其算法对于所有连续体结构都适用，是一个极为有效的方法[2]。

Ansys提供了以有限元为基础的结构优化设计功能，可以进行全面的尺寸优化、形状优化和拓扑优化，为产品设计提供了一个很好的平台，并在实际工程应用中取得了很好的效果。在产品设计阶段，灵活运用各种拓扑优化技术，可以确定材料的最佳分配方案，以便对结构进行改进设计，节约生产成本，实现产品经济、高效的设计。

图1 旋回架结构Fig.1 The structure of cycle frame

1 均匀化法拓扑优化

1.1 均匀化法原理

均匀化方法（Homogenization Method）是一种具有十分严密的力学和数学基础的材料描述方法。它在连续体结构拓扑优化设计的工程运用十分广泛，并取得了很好的效果。1988年Bendsoe和Kickuchi将结构拓扑优化归结为材料在一定区域内的优化分布问题，建立了基于微结构概念和均匀化理论的拓扑优化理论，把复杂的拓扑优化问题转化成广义上的尺寸变量问题，为拓扑优化的求解提供了一个新思路[3]。它的基本思想是：由微结构的形式和尺寸参数决定宏观材料的密度和弹性性质出发，在进行优化求解的过程中，把微结构单胞引入组成拓扑结构的材料中，用尺寸固定的孔洞微结构的单胞构造设计区域，并以微结构的单胞尺寸为优化设计变量，把材料密度、弹性模量等参量表示成微结构单胞尺寸变量的函数，通过单胞尺寸的消长来实现微结构的增删，若孔洞变大到整个微结构，则该微结构消失，即材料被去除，形成伪密度为0的区域。若孔洞变小以致消失，则该微结构被填充，也即材料得以保留，形成伪密度为1的区域。若优化结束时，还存在微结构，则该区域由某种复合材料组成，也即是伪密度在0-1的中间区域。通过此种方法使得结构拓扑优化模型与尺寸优化模型的统一和连续化。

1.2 均匀化法拓扑优化数学模型

根据Bendsoe和Kickuchi提出的均匀化理论和微结构概念，以微结构单胞密度为设计变量，柔顺度最小为目标函数，约束条件为体积限定的情祝下，建立均匀化方法的拓扑优化数学模型。其

高校扩招政策对城乡不同收入群体的影响也存在差异。其中，扩招政策对城乡低收入群体产生的影响表现为对农村50%以下低收入群体收入影响并不显著，但对城镇居民50%以下低收入群体产生显著的正向影响，同时高校扩招政策对城乡低收入群体教育产生了扩大的“马太效应”。进一步地，可以发现农村居民高收入组的教育回报率为6.9%，高于城镇居民的4.1%，结合扩招政策对城乡居民教育回报和收入回报的影响可以发现，高校扩招政策导致城乡居民高收入群体组的教育差距扩大，但在一定程度上缩小了高收入群体城乡间的收入差距。

采用均匀化方法求解扑拓扑优化问题，一般分为3 个步骤[4]：

①复合材料力学为基础，由最小势能原理出发并结合均匀化理论的微元体假设，并由公式

得到材料特征参数χkl。然后利用公式

②用有限元方法求解结构位移场和其他性能指标。

③采取一定的优化算法更新设计变量，并保证计算过程的稳定性和收敛性。

2 基于Ansys的托架拓扑优化分析

2.1 基于Ansys的拓扑优化

Ansys软件的拓扑优化技术采用的是均匀化方法。主要过程为：首先在每个有限元单元内构造微结构单胞，微结构的形式和尺寸决定了单元的弹性性质和密度；优化过程中，以微结构的单胞尺寸作为拓扑优化设计变量，以单胞尺寸的消长实现微结构的增删；经过多次迭代计算，结构中产生不同尺寸的孔洞，从而达到拓扑优化之目的[6]。

Ansys的拓扑优化不需要人为去定义优化参数，而是自动将材料分布当作优化参数。在进行拓扑优化分析时，同其他有限元分析一样定义几何结构、有限元模型、施加载荷和边界条件等，然后定义优化分析的目标函数，从而定义约束参数。拓扑优化的目标即目标函数是在满足给定的实际约束条件下（如体积减小等）需要极大或极小的参数，通常采用的目标函数是结构柔顺度极小化或基频最大等[7]。

Ansys进行拓扑优化的一般过程为：

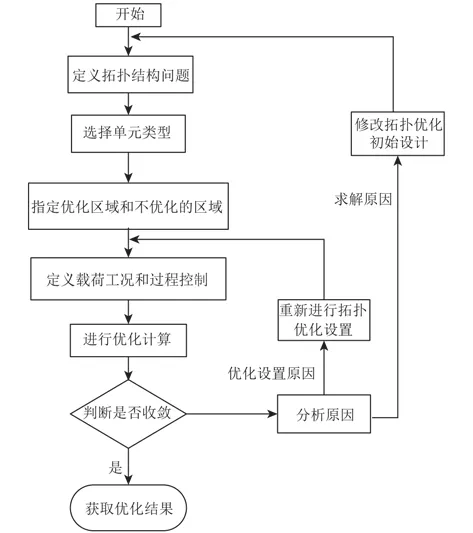
图2 Ansys拓扑优化流程图Fig.2 Topology optimization flow chart of Ansys

2.2 拓扑优化前处理

托架的设计优化区域为托架的侧板部分。如图3所示，区域1（耳轴、底板）为不优化的区域，区域2（侧板）为优化区域。从PROE中导入托架的三维模型，设定单元尺寸为20 mm，对托架用六面体划分网格。托架所用材料为铝合金材料7A52，其相关参数如表1所示。

图3 托架优化区域与不优化区域Fig.3 Optimized area and not optimized area

表1 7A52材料特性Tab.1 The material characteristics of 7A52

优化计算时考虑水平射击和垂直射击2种工况，2种工况基本涵盖了托架的正常使用受力情形。计算中的载荷为火炮射击最大后座力160 kN，载荷以轴承载荷的方式平均加到两侧托架的耳轴内环面上，因此每个托架承受载荷为80 kN，计算中约束加在底板的底面。

2.3 拓扑优化求解

利用Ansys的参数化语言对托架进行拓扑优化求解控制，其命令流如下：

TOCOMP，MOCOMP，MULTIPLE，2

！将多柔度MOCOMP（考虑2个载荷工况）定义为拓扑优化函数

TOVAR，MOCOMP，OBJ

！将MOCOMP定义为目标函数。

TOVAR，VOLUME，CON，80

！定义约束函数VOLUME，约束条件为体积缩小80%。

TOTYPE，OC

！选用OC方法进行拓扑优化求解

TODEF，0.00001！定义优化收敛精度为0.0001

TOLOOP，50，1！自动进行50次优化迭代计算

2.4 拓扑优化后处理

1）托架结构的节点和单元伪密度云图如图4和图5所示（2色显示）。图中区域1的伪密度值为1，表示该区域的材料应该保留。区域2的伪密度值为0，表示该区域的材料应该被去除。通过伪密度云图，可以得到托架结构材料的最佳分配和托架结构改进的大致方案。

图4 托架的节点伪密度云图Fig.4 Node false density plot of bracket

图5 托架的单元伪密度云图片Fig.5 Element false density plot of bracket

2）托架的目标函数和约束函数迭代曲线如图6和图7所示。目标函数迭代曲线表明，在迭代计算的过程中托架结构柔顺度的变化趋势情况，托架经过27次迭代收敛，结构柔顺度由最初的13.481 N·m逐渐减为6.012 N·m。约束函数的迭代曲线表明，在迭代计算过程中体积的变化趋势情况，迭代过程中体积始终在8.96×10–3m3附近波动，最后趋于稳定，与最初托架的体积4.39×10–2m3相比，体积减小了80%。

图6 目标函数迭代曲线Fig.6 Iterated curve of objective function

图7 约束函数迭代曲线Fig.7 Iterated curve of constraint function

3 托架结构可制造化改进

因拓扑优化设计只是一种概念设计，其优化结果极不规则，不便于加工和制造，所以必须对优化结果进行可制造化处理。根据图4和图5中的拓扑优化结果，左边深色部分为密度值为0的区域，对其进行挖孔处理，浅色部分为材料堆积的位置，对其进行适当延宽并加肋。结合制造工艺，建立托架的新结构如图8所示。对改进后的托架结构进行有限元静力分析，其改进前后结构的相关参数对比如表2所示。

从表2的比较结果可以看出改进后的结构在质量减少16%的情况下，托架结构最大应力基本没有变化，最大变形减少了15%。且托架用所用铝合金材料为7A52，其屈服极限在255 MPa以上，优化后的结果满足了强度、刚度性能的要求，达到了结构轻量化设计的目的。

图8 改进后的托架结构Fig.8 The improved bracket structure

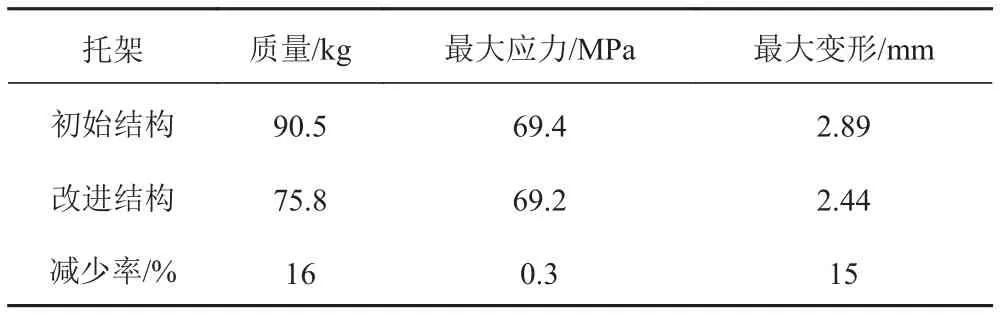
表2 改进前后托架相关参数对比Tab.2 Comparison of the relevant parameters before and after improvement

4 结 语

本文运用拓扑优化中的均匀化理论，通过Ansys软件提供的拓扑优化功能，对某型舰炮托架进行了拓扑优化研究，解决了以往按经验设计的局限。经过拓扑优化设计改进后的托架与初始结构相比，托架结构质量减少了16%，最大应力基本没有变化，最大变形减少了15%，实现了托架轻量化设计的目的，证明拓扑优化设计的可行性。这对于舰炮结构改进设计具有工程应用价值，对其他一般机械结构问题也提供了一种设计思路。

[1]曹德乐.基于拓扑优化的发罩内板筋条结构正向设计[J].装备制造技术, 2015, (5): 111–114.

[2]孙蓓, 苏超.拓扑优化均匀化方法的改进迭代算法[J].河海大学学报, 2010, 38(1): 47–51.

[3]王明强, 徐健.基于均匀化法的风雨载荷下折叠式舱口盖拓扑优化设计研究[J].船舶工程, 2014, 36(1): 10–13.

[4]左孔天, 陈立平, 钟毅芳, 等.基于人工材料密度的新型拓扑优化理论和算法研究[J].机械工程学报, 2004, 40(12): 31–37.

[5]左孔天.连续体结构拓扑优化理论与应用研究[D].武汉: 华中科技大学, 2004: 17–20.

[6]胡松, 黄勇, 陈波, 等.基于石膏空腔模的无梁楼盖拓扑优化及拓扑结构静力特性研究[J].空间结构, 2015, 21(1): 54–63.

[7]博弈创作室.ANSYS9.0经典产品高级分析技术与实例详解[M].北京: 中国水利水电出版社.