交流系统故障对直流线路影响的量化分析
2018-03-26王江亭刘宇石但扬清王维洲刘文颖
王江亭,刘宇石,但扬清,王维洲,刘文颖
(1.国网甘肃省电力公司,甘肃 兰州 730050;2.中国电力科学研究院,北京 100192;3.国网浙江省电力公司经济技术研究院,浙江 杭州 310008;4.华北电力大学,北京 102206)
0 引言
当今社会,电网技术飞速发展,用电负荷急速增长,电力网络也越来越复杂。尤其是交直流电网混联日益加深,电网由传统的强交弱直系统逐渐向强直弱交演化。随着交直流混联电网之间互联程度的加深,电网对于防范局部扰动,如交流侧故障而引起的直流侧故障的连锁反应能力随之减弱。交直流混联电网的连锁故障已经威胁到电网的安全稳定运行。
在交直流系统相互影响方面,国内外众多学者已经做了许多有益的探索研究。文献1—5均指出,交流系统故障对直流线路的影响主要体现在:直流线路可能由于交流侧母线的故障致使电压幅值过低或使交流侧换相电压过零点的相角发生变化,进而导致换相失败,严重时会引发直流闭锁、直流功率传输中断。然而,这些研究仅定性分析了交流系统故障对直流系统的影响,而无法从定量角度上判断交流系统故障对直流系统影响的大小,不能对交直流混合运行电力系统连锁故障后续的建模及分析提供有效依据。下面在分析交流系统故障对直流线路影响的基础上,提出了电压增积指标,旨在定量描述交流系统故障对直流线路的影响。
1 交流系统故障对直流线路的影响
交流系统故障对直流线路的影响,最常见的就是导致换流器换相失败,造成直流线路闭锁,引起潮流转移,从而引发连锁故障。
直流线路逆变侧交流系统发生三相短路故障,使逆变器交流母线电压降低,从而使逆变器的反电动势降低,直流电流增大,可能引起换相失败。交流电压下降的大小及速率与交流系统的强弱及故障点离逆变站的远近有关。当故障点较近及交流系统较弱时,换相电压下降幅度大且速率快,最容易引起换相失败(参见文献6)。
由直流换流原理可知,逆变器的触发角α、超前触发角β、关断角γ和换相角μ之间关系:

逆变器的直流电压、换相角和关断角可分别用以下公式表示:
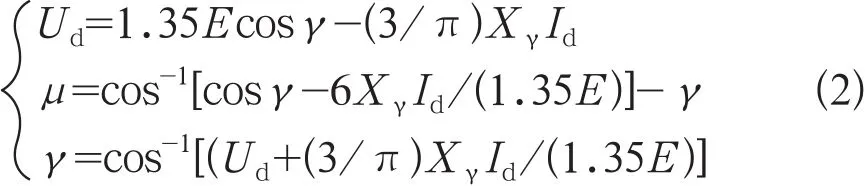
式(2)中,E为逆变器换相线电压的有效值;X为逆变器的等值换相电抗;Ud为逆变器的直流电压;γ为逆变器的关断角;Id为直流电流;μ为逆变器的换相角。
当交流系统发生三相短路时,换相电压E降低,直流电流Id升高,由式(2)可知,逆变器的直流电压Ud随之降低,与此同时会导致关断角γ减小。晶闸管换流阀恢复阻断能力所用的最小时间对应的关断角为γmin约为7.2°。当γ角小于γmin时,将导致逆变器换相失败。
交流系统故障使逆变器换相电压下降,逆变侧关断角减小,从而引起换相失败;如果长时间换相失败,可能最终导致直流线路闭锁。在电力系统中,一般来说,当逆变侧交流电压E下降到0.6(标幺值)时,会致使直流线路逆变器γ角小于γmin而发生换相失败,换相失败持续6—8 s就会造成直流线路闭锁。
在强直弱交混联电网中,直流线路输送功率一般大于交流线路输送功率。交流系统故障导致直流闭锁引起潮流大转移的情况下,可能会引起交流系统大范围的连锁反应,使电网发生大面积停电事故。因此,对交流系统故障对直流线路的影响进行量化分析具有重要意义,可为辨识交流线路的重要度提供理论依据,进而防止交直流电网连锁故障发生。
2 交流系统故障对直流线路影响的量化指标
2.1 量化指标——电压增积
当系统在正常状态或故障状态下运行时,可以作出直流线路电压统计图,其纵坐标为直流线路的逆变侧电压值,横坐标为直流线路编号。对这些离散的点进行曲线拟合,得到电压统计拟合曲线。将运行在正常状态下的电压统计拟合曲线与故障状态下的电压统计拟合曲线绘制于同一图中,并进行加权,可求得2条加权曲线所夹的面积,称这个面积为电压增积。
根据交直流交替解耦算法得到各直流线路逆变侧电压值,对电压值进行降序排列,并对直流线路进行标号。上面提出的量化指标认为,交流系统故障对n回直流线路的影响(Infl),可以等效成交流线路故障后n回直流线路逆变侧电压统计拟合曲线与故障前直流线路逆变侧电压统计拟合曲线之间的面积,即:
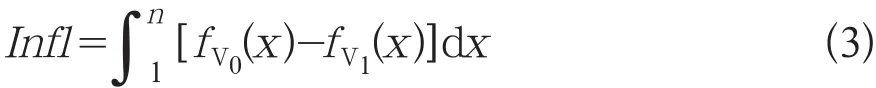
式(3)中:n为直流线路数量;fV0(x)为故障前直流逆变侧电压统计拟合曲线函数;fV1(x)为故障后直流逆变侧电压统计拟合曲线函数。
由于通过交直流交替解耦算法计算所得实验数据为离散的点,若要求得上述面积,需要对实验数据进行曲线拟合。
曲线拟合是指对实验所得到的数据进行拟合,找出一条逼近但不需要经过每个数据点的光滑简单曲线,并能反映实验数据的变化趋势,以便于计算;要求使拟合函数与原始数据的残差平方和最小。把A点的拟合逼近值S(xA)与实验所得数据值yA的差值称为拟合曲线在A点的残余偏差δA,即δA=S(xA)-yA。而用所有点的残差平方和最小,即来确定参数,拟合所需曲线的方法,称为曲线拟合的最小二乘法,具体步骤如下。
(1) 对于给定的一组实验所得数据{(xi,yi),i=0,1…,m}(n<m),设拟合函数为:
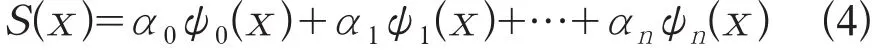
式中:ψ0(x),ψ1(x),…,ψn(x)为线性无关的包含x的初等函数。
(2) 求各数据点的残余偏差平方和:
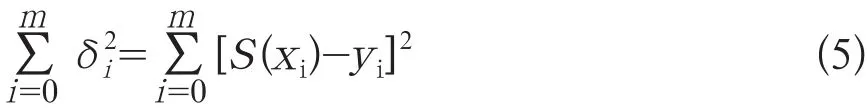
(3)使(5)式中的残余平方和最小的必要条件:
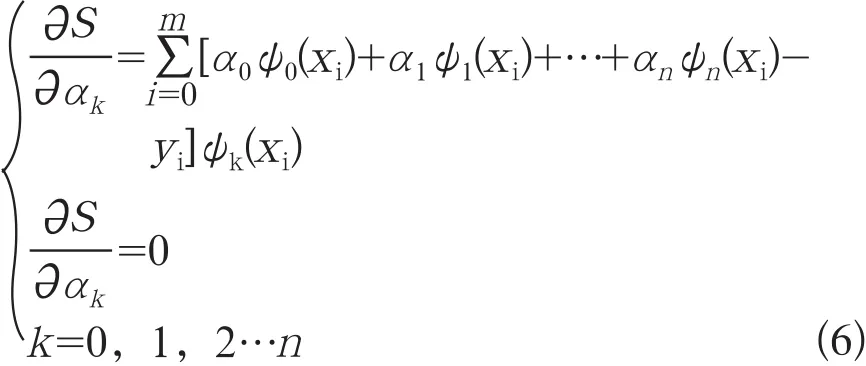
(4) 求得一组系数α0,α1…αn,即可得到所求的拟合曲线方程。
另一方面,潮流转移理论认为,线路传输的功率越大,故障后对周围线路的潮流转移量就越大,也就是说故障后对周围线路的影响越大,这条线路也就越重要。为了更明确地区分,根据潮流转移理论,可以对原始数据用直流线路功率进行加权:

式中:Vw为加权后的结果(即加权值);w为权值;V为直流线路逆变侧电压值。
为方便计算,取直流线路中传输功率最小值为基准值,则w为Pi与基准值的比值:
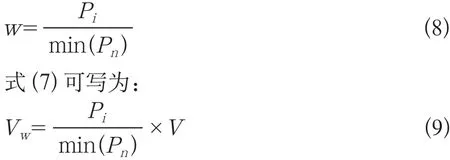
代入式(3)可得加权后的交流故障系统对直流线路影响的电压增积计算公式:

式(10)中:V0(x)为故障前直流线路逆变侧电压;V1(x)为故障后直流线路逆变侧电压。
2.2 量化指标计算流程
基于对电压增积的分析,给出交流系统故障对直流线路影响的量化指标计算流程,如图1所示。

图1 交流系统故障对直流线路影响的量化指标计算流程
(1) 首先基于电网基础数据,分别计算正常运行状态和交流故障状态下的直流线路逆变侧电压V0,V1。
(2) 利用式(9)对V0,V1进行加权。
(3) 对加权值进行曲线拟合,得到fvw1(x)和fvw2(x)。
(4) 利用式(10)计算电压增积。
(5) 根据不同线路计算所得电压增积,对线路的影响进行量化比较分析。
3 算例分析
采用中国电力科学研究院的PSD电力系统分析软件工具中的PSD-BPA为仿真工具,该软件包主要由潮流和暂稳程序构成,具有计算规模大、计算速度快、数值稳定性好、功能强等特点。现以南方电网2015年夏大运行方式下的基础数据为来源进行仿真计算,结合以上提出的量化指标进行量化分析,分析交流故障对直流线路影响的情况。该运行方式下,500 kV以上交流线路共有434条,直流线路共有7条,500 kV变电站共有121个。
3.1 直流线路逆变侧电压加权值
在该运行方式下,分别在正常运行状态、故障1(桂林—贤令山双回交流线故障)、故障2(故障1+柳东—贺州双回交流线故)、故障3(故障2+东莞—福园双回交流线故障)情况下,计算南方电网所有直流线路逆变侧电压值,如表1所示。

表1 故障1—3前后直流线路逆变侧电压
对故障1—3前后的直流线路逆变侧电压按式(9)进行加权计算,如表2所示。

表2 故障1—3前后直流线路逆变侧电压加权值
3.2 电压增积
基于最小二乘法,利用MATLAB仿真软件对表2中的数据进行曲线拟合。应用Rational为回归类型对故障前的加权数据进行拟合所得到的曲线(见图2)的标准差最小,即最小。Rational为回归类型的曲线拟合:

利用回归类型为Rational,得到表2中故障前曲线拟合函数为:

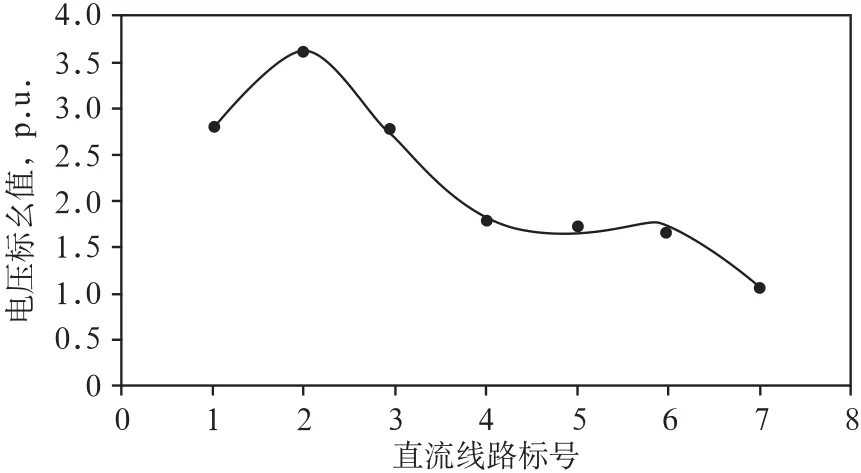
图2 故障前电压加权值统计拟合曲线
对于表2中故障1—3后的数据,同样应用Rational为回归类型对故障后的加权数据进行拟合所得到的曲线(见图3)的标准差最小,即最小。同理,可得故障1—3后数据曲线拟合函数分别为:

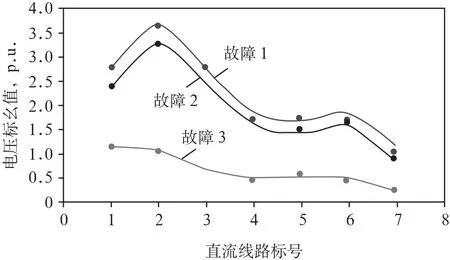
图3 故障后电压加权值统计拟合曲线
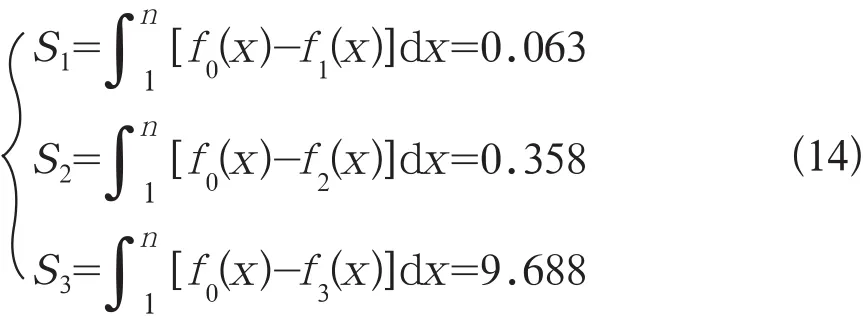

图4 各故障的电压增积
上式中数值代表交流系统故障对直流系统影响的量化值,若为负数代表故障后的加权值降低。
从上式可以看出,故障2对直流线路的影响介于故障1和故障3之间,这是符合实际的。
计算电压增积的比值,得到:

由上式可知,交流故障2对直流线路的影响是交流故障1对直流线路影响大小的6倍。因此,电压增积可以作为交流系统故障对直流线路影响的量化指标。
4 结论
以上考虑了不同交流系统故障对直流线路的影响,并考虑了用直流线路传输功率进行加权,更好地反映直流系统间的差别。在此基础上提出了电压增积这一量化指标,有效地对交流系统故障对直流线路的影响进行量化分析,并以南方电网为例验证此方法的可行性。利用以上提出的方法可以有效地找出交直流混联电网中交流系统风险较大的故障模式,并在此基础上,采取应对措施,保障交直流混联电网的安全稳定运行,对防止交流系统薄弱环节出现问题具有一定的指导作用。
1 赵建伟,厉天康,严 正,等.交直流电网连锁故障研究现状与展望[J].华东电力,2013,41(4):720-724.
2 徐 政.交直流电力系统动态行为分析[J].高电压技术,2004,28(6):3.
3 余晓鹏,张雪敏,钟雨芯,等.交直流系统连锁故障模型及停电风险分析[J].电力系统自动化,2014,38(19):33-39.
4 鲁德锋,毛为民,冼伟雄.直流站换流失败引起继电保护不正确动作分析[J].电力安全技术,2006,8(1):35-37.
5 陈建华.电力系统连锁故障预测初探[D].天津:天津大学,2005.
6 黎敬霞,钱 晶,李 捷,等.换流站交流侧故障对HV DC系统的影响[J].云南电力技术,2007,35(3):10-12.
7 马玉龙,肖湘宁,姜 旭.交流系统接地故障对HVDC的影响分析[J].中国电机工程学报,2006,26(11):144-149.
8 郭启伟,汪希伟,李 超,等.大电网故障下的银东直流动态特性研究[J].电力安全技术,2016,18(3):8-13.
9 何朝荣,李兴源,金小明,等.高压直流输电系统换相失败判断标准的仿真分析[J].电网技术,2007,31(1):20-24.
10 唐家德.基于MATLAB的非线性曲线拟合[J].计算机与现代化,2008,70(6):15-19.
11 陈岚峰,杨静瑜,崔 崧,等.基于MATLAB的最小二乘曲线拟合仿真研究[J].沈阳师范大学学报(自然科学版),2014,32(1):75-79.
12 曾长雄.离散数据的最小二乘曲线拟合及应用分析[J].岳阳职业技术学院学报,2010,25(3):96-99.
