识别流网络关键节点的虚拟外界投入产出分析法

朱为华，刘 凯，闫小勇，汪 明，吴金闪

(1.北京师范大学地表过程与资源生态国家重点实验室 北京 海淀区 100875；2.北京师范大学环境演变与自然灾害教育部重点实验室 北京 海淀区 100875；3.北京师范大学地理科学学部 北京 海淀区 100875；4.北京交通大学交通系统科学与工程研究院 北京 海淀区 100044；5.北京师范大学系统科学学院 北京 海淀区 100875)

许多实际的复杂系统都可以抽象为节点之间存在物质、能量或信息等流动关系的流网络[1]。典型的流网络包括金融机构之间有资金流动的金融网络[2]、地点之间有客流或货流的交通运输网络[3]、论文之间存在引用关系(一种信息的流动)的科学引文网络[4]、物种之间存在能量流动的食物链网络[5]等。在这些流网络的复杂性研究中(实际上是整个复杂网络研究领域中)的一个核心问题是：如何对网络中的关键节点进行识别[6-8]？在这里，节点是否“关键”或者说节点的“中心性”可以根据所研究问题的特点而有不同的衡量标准。如，从网络拓扑结构的角度，可以认为拥有更多直接或间接邻居的节点更为重要，据此可定义度中心性、H指数[9]、核数[10]等节点中心性评估指标；从网络中节点间最短路径的角度，可以认为通过最短路径最多的节点或与其他节点的平均最短距离最小的节点更为重要，据此可定义介数中心性[11]或邻近中心性[12]等指标。类似地，还有很多节点中心性指标可以从网络结构或功能的不同角度来进行定义，文献[6-7]对主要的网络节点中心性指标进行了非常全面的综述和深入的讨论。本文更为关心的是：在一般的含有流的复杂网络中，如何衡量节点在整个流网络系统中的影响力——这种影响力既包括节点出入流的直接影响(如在一个草原生态系统中，植物对食草动物的能量流供给)，也会考虑节点间的间接影响(如植物间接供给捕食食草动物的禽兽的能量)。

经济学中的投入产出分析法[13]为前述问题提供了一种可以借鉴的解决手段。标准的投入产出分析法是用来处理国民经济系统中生产和消费部门之间的投入产出问题的一种方法。在这种系统中，每个生产部门都会生产产品，一部分可能被用于最终消费部门的消费，另一部分可能被作为生产资料投入到其他部门的生产活动中。通过假设删除某一个部门后，观察系统总产出的减少量，即可作为评估该生产部门重要性的一种指标。投入产出分析法很容易从部门构成的经济网络扩展应用到很多其他网络系统中。如可以将食物链网络中的每个物种看成一个部门，物种A食用物种B就可以看作是部门B投入给了部门A。但是，标准的投入产出分析法只能用于带有外界消费部门的开放系统中。而对于一些实际的流网络系统，这样的外界可能并不直接存在(例如科学引文网络)或者外界的流入流出数据并不容易获得(例如交通运输网络)。对于这样缺乏外界的封闭流网络系统，标准的投入产出分析法并不能直接应用。最近，文献[14]提出一种对封闭流网络的投入产出矩阵施加微扰求取逆矩阵的方法来计算网络中节点的影响力，并应用于学科领域影响力的评估问题中。但在这种方法的计算过程中，由于施加的微扰破坏了矩阵的稀疏性，导致计算效率降低，难以应用于大规模封闭流网络的关键节点识别。

本文提出另外一种基于投入产出分析法的封闭流网络关键节点识别方法。在封闭流网络系统中引入一个虚拟的外界节点，并将此外界节点与网络中的所有节点建立双向连接，同时设置外界节点到网络某原有节点的流入量等于该节点实际流出量的总和，设置从网络某原有节点到外界节点的流出量等于该节点实际流入量的总和。通过这种方式处理后，就可以直接将标准的投入产出分析法应用到封闭流网络系统的关键节点识别中。本文将首先介绍这一方法的原理和细节，然后给出这一方法的应用实例，并将其评估结果与一些流网络关键节点识别经典算法的结果进行对比。

1 虚拟外界投入产出分析

1.1 投入产出分析

投入产出分析是研究经济系统中各个部门之间投入与产出的相互依存关系的一种经济数量方法[13]。假设某经济系统中共有N个部门，用表示部门i投入到部门j的价值，则部门间直接的投入产出系数可定义为第j部门产出单位价值所消耗第i部门的价值：

式中，X j表示部门j的总产出价值：

如果令其中的部门N表示最终消费者，则其他部门投入到部门N的价值可记为：

根据式(1)～式(3)，有：

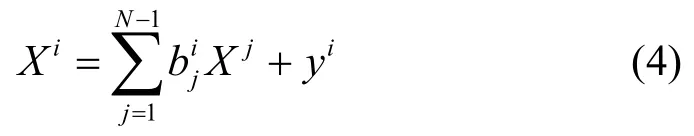
于是前N−1个生产部门的产出量可以写成如下形式：

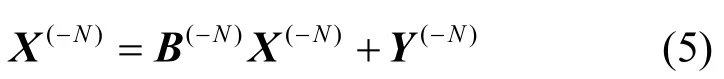
式(5)也可以写成如下形式：

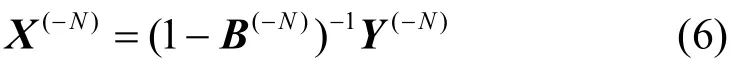
1.2 虚拟消去法

虚拟消去法(hypothetical extraction method,HEM)[15]是传统投入产出分析中用来衡量某个部门k的重要性的一种标准方法。HEM通过假设从N−1个生产部门中删除一个部门k，然后计算新的系统中剩余的N−2个生产部门的产出量：

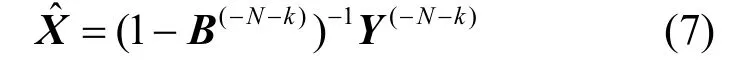
式中，Y(−N−k)是删除第k和第N个元素后的Y向量；是删除第k和第N个部门后的投入产出矩阵。那么，部门k的重要性就可以用去除部门k后系统总的产出量相对于原系统中总的产出量的减少比例Hk来衡量：

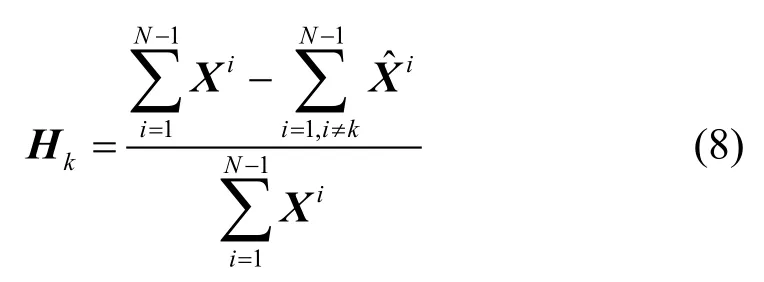
H k越大，说明部门k在整个经济活动中的地位越重要。

1.3 虚拟外界的引入

前述投入产出分析法和HEM很容易扩展到一些流网络系统的节点中心性评估问题中，只要网络中存在节点i到j的流量，并且存在一个最终汇入所有其他节点剩余流量的外界节点。食物链网络是一个符合上述要求的典型网络。在食物链网络中，某物种节点上产出的能量除了被另一些物种节点消耗外，剩余的部分会耗散到“自然界”这个外界节点中。像食物链网络这种存在实际外界节点的系统和存在最终消费者的经济系统，都可以被称为是开放网络流系统。但在更多一般的流网络中，像最终消费者这样的和产业部门不一样的外生部门是很难找到的，将这种不存在或不显式存在外界节点的流网络系统称为封闭流网络系统。为评估封闭流网络系统中各节点的重要性，受文献[16]的启发，本文提出一种为网络增加虚拟外界节点的方法。文献[16]提出的LeaderRank算法，通过在原始网络中添加一个超级节点与所有节点双向相连的方法，能够处理社交网络的节点影响力排序问题。本文将这种方法推广到一般的封闭流网络中：本文在网络中增加一个虚拟的外部节点n，并且将它与网络中已有的所有节点双向连接，并设置外界节点到网络某原有节点的流入量等于该节点实际流出量的总和，设置从网络某原有节点到外界节点的流出量等于该节点实际流入量的总和。通过这种方式处理后，就可以直接将式(1)～式(8)中标准的投入产出分析法应用到封闭流网络系统的关键节点识别中。

1.4 计算方法

在使用式(7)计算删去节点k后系统的产出量时，涉及到矩阵1−B(−N−k)的逆矩阵求解，对于大规模的网络这一过程是较为耗时的。在这里本文可以使用简单迭代法[17]来求解。由于式(7)可以化为等价的方程组：

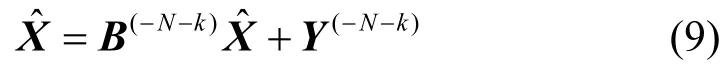
根据上式构造如下迭代公式：

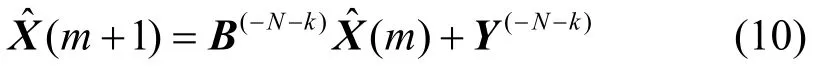
式中，m为当前迭代次数，初始条件可取根据式(1)可知投入产出矩阵B是一个列归一化矩阵，其最大特征值为1[13]。而迭代矩阵B(−N−k)是在B中删去了两行两列，因此其最大特征值(即谱半径)一定小于1。由线性方程组简单迭代法收敛的充分必要条件是迭代矩阵谱半径小于1[17]可知，式(10)的迭代过程一定收敛。在本文的后续实例计算中，本文设定的迭代控制条件为

2 虚拟外界投入产出分析在铁路网络关键站点识别中的应用

2.1 数据与网络构建方法

本文通过一个中国铁路网络关键站点识别的实例来演示虚拟外界投入产出分析法的应用过程。本文所采用的实验数据包括：1)2015年中国铁路网络矢量地图，数据下载自OpenStreetMap；2)2015年中国铁路开行的所有客运车次，数据下载自中国铁路客户服务中心网站。首先基于铁路网络矢量地图数据构建了2015年的中国铁路网络拓扑结构。为了便于分析，对上述铁路网络进行适当简化，只保留了每个客运车次的首末站，以及铁路线路交叉点处的车站，并合并了相应的连边。得到的简化铁路网络中共有节点529个，有向边1 356条。

将车站作为投入产出模型中的各个部门，将两个相邻车站间的运行车次数量作为投入或产出的流量，建立起含流的铁路网络系统。在此基础上，加入一个虚拟的外界节点和每个节点进行连接，并设置虚拟节点到各个节点的流量等于该节点流出量的和，各个节点到虚拟节点的流量等于该节点流入量的和。

2.2 投入产出分析法的评估结果

将式(8)中的投入产出虚拟消去法应用于上述铁路网络的节点重要性评估，可以发现投入产出模型得到的重要站点在中国铁路网络的地理空间上分布集中，主要分布在京沪线、京广线和京哈线3条重要的线路上。京哈-京广线连接了华北、华中与华南，是我国铁路网的中轴和运量最大的南北大动脉，因此该线路上的站点是极为重要的铁路枢纽；京沪铁路经过东部人口密集、经济发达地区，沿线有许多重要工业城市，站点发车次数多，当站点去除后，对中国东部沿海的经济以及人员流动影响巨大。有针对性地对投入产出法识别出的这些重要站点加权保护，对维持网络整体运输能力和提升铁路网络的鲁棒性都具有实际意义。

2.3 与PageRank算法的对比

PageRank算法[18]是识别流网络中关键节点的常用方法，其基本思想是：网络中一个节点的重要性取决于指向它的其他节点的数量和重要性。本文将PageRank算法用于中国铁路网络的关键站点识别问题中，结果显示PageRank算法识别出的重要站点主要分布在每个区域路网的局域中心上。

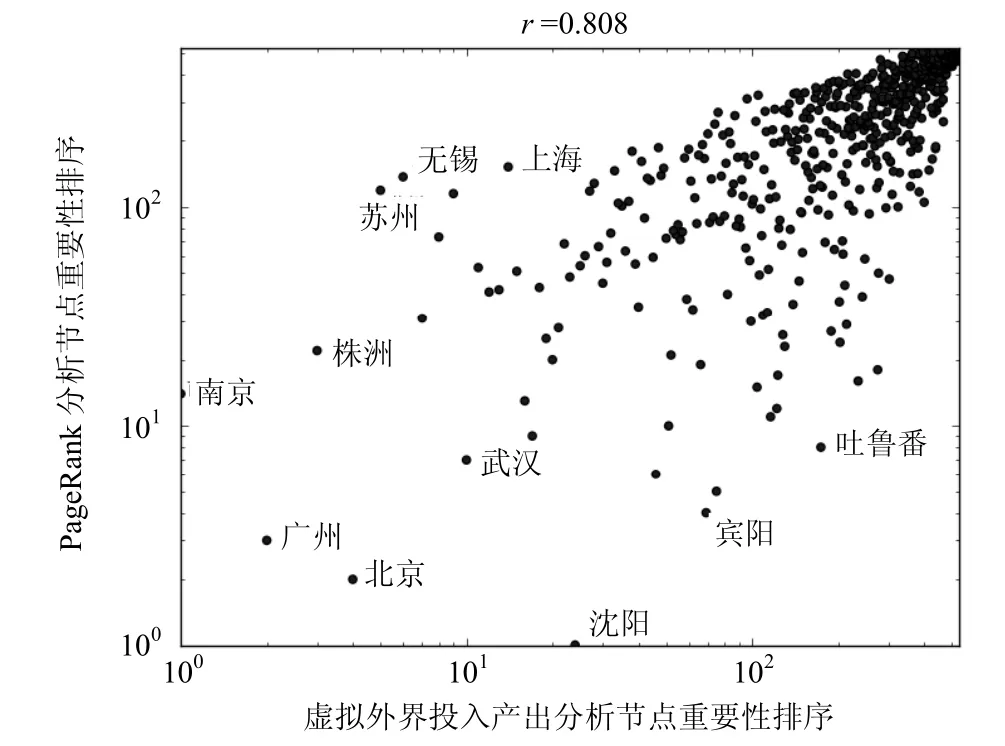
图1 投入产出和PageRank算法得到的铁路网络站点重要性排序对比

图1给出了投入产出方法和PageRank算法得到的站点重要性排序对比结果。从图1中可以看到，PageRank算法与投入产出法得到的站点排名整体上具有一定的相关性，两者的皮尔森相关系数r=0.808。对于一些公认的重要站点(如北京、广州和武汉等)，两种方法都给出了近似的排序。但是在有些站点的排序中两种方法的结果差异较大。例如，宾阳站和吐鲁番站在PageRank算法中分别排第4名和第8名，而这两个站点的投入产出排名则分别为第69名和第174名。宾阳站位于中国南部地区，站点的运行车次较少。但在宾阳站的3个邻居站点中，排名17南宁站的68%的车次、排名67的柳州站50%的车次以及排名81的贵港站52%的车次都通过了宾阳站，这使得宾阳在PageRank算法的结果中取得了更高的排名，体现了PageRank算法“节点的重要性取决于指向它的其他节点的数量和重要性”这一思想。但PageRank算法认为宾阳站的重要性在全国铁路站点中排名第4，与该站点在铁路运输系统中的实际地位并不相符。相较而言，本文的投入产出方法对该站点的排序则更为可信。上海站是另外一个典型的例子：该站在投入产出方法中排名14位，而在PageRank算法排名中则只位于152位。整体而言，投入产出分析法给出的站点重要程度排序与人们对车站重要性的直观认识更为符合。

3 虚拟外界投入产出分析在世界粮农贸易网络关键节点识别中的应用

本节以世界粮农贸易网络作为分析对象，进一步对虚拟外界投入产出分析法的应用过程和特点进行说明。

3.1 数据与网络构建方法

本文所分析的世界粮农贸易网络数据集来自于文献[19]，该数据集记录了2010年全世界主要国家和地区之间的粮农进出口贸易额。本文将国家(或地区)作为投入产出网络中的各个节点，将国家(或地区)A出口到国家(或地区)B的粮农贸易额作为节点A到B的流量，建立起含流的世界粮农贸易网络。该网络共包含节点213个，有向边13 440条。图2选取了流量排名前100的连边绘制的世界粮农贸易骨架网络，该网络中的进出口贸易额占原始网络总贸易额的49.7%。图中节点大小正比于相应国家或地区的粮农进出口总额，连边粗细正比于节点间贸易量。使用1.3节的方法，本文在原始网络中加入一个虚拟的外界节点和每个节点进行连接，并设置了虚拟节点到各个节点的流入流出量。

3.2 投入产出分析法与PageRank算法结果对比

本文分别将式(8)中的投入产出虚拟消去法和文献[18]中的PageRank算法应用于国际粮农贸易网络的节点重要性评估，得到的排序结果对比如图3所示。从图中可以看到，两种方法的排序结果整体上具有一定的相关性，皮尔森相关系数r=0.703。这说明对于多数国家来说，这两种方法给出的排序结果是较为接近的，如图3中的中国、美国、德国等。但是仍有一些国家(或地区)在这两种方法给出的排序结果上有较大差异。如，PageRank算法对巴西、阿根廷等国家的排序远低于投入产出分析法的排序，而对日本、沙特阿拉伯、香港、澳门等国家或地区的排序则远高于投入产出方法的排序。

本文分别以巴西和日本这两个国家为例，结合图2和图3，进一步分析在世界粮农贸易网络中投入产出和PageRank两种方法对节点重要性排序差异的原因。巴西的粮农进出口总额中87.8%是出口额，是一个典型的粮农出口国家。在巴西的粮农出口总额中，34.9%的粮农产品出口给了中国(在投入产出分析法中排名第2位)，因此巴西在整个国际粮农贸易系统中的投入产出排名就更高(排名第6位)。而巴西的进口粮农产品主要来自阿根廷(见图2)，由于阿根廷的PageRank排名很低，导致巴西的PageRank排名也不高。另一方面，从图2中可以看到，日本是一个典型的粮农进口国家，从PageRank排名前两位的美国和中国进口了超过进口总额44%的粮农产品。根据PageRank“节点的重要性取决于指向它的其他节点的数量和重要性”的思想，日本的PageRank排名高达第4位。但日本粮农出口额很小，只占进出口总额的7.2%，因此其对于整个粮农贸易系统的总产出贡献很低，投入产出排名自然也较低，只列第18位。综合比较，投入产出方法更为合理地反映出了不同国家和地区在整个世界粮农贸易网络中的影响力。

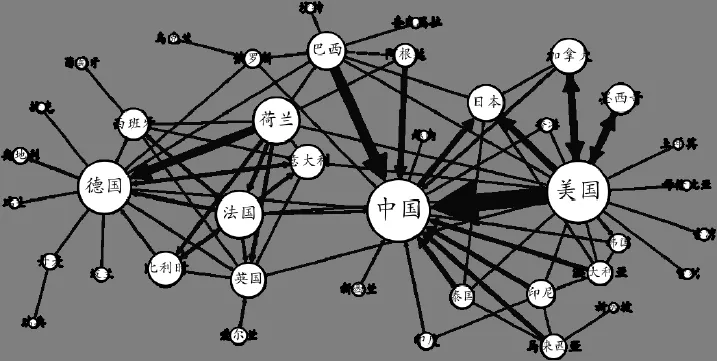
图2 世界粮农贸易骨架网络

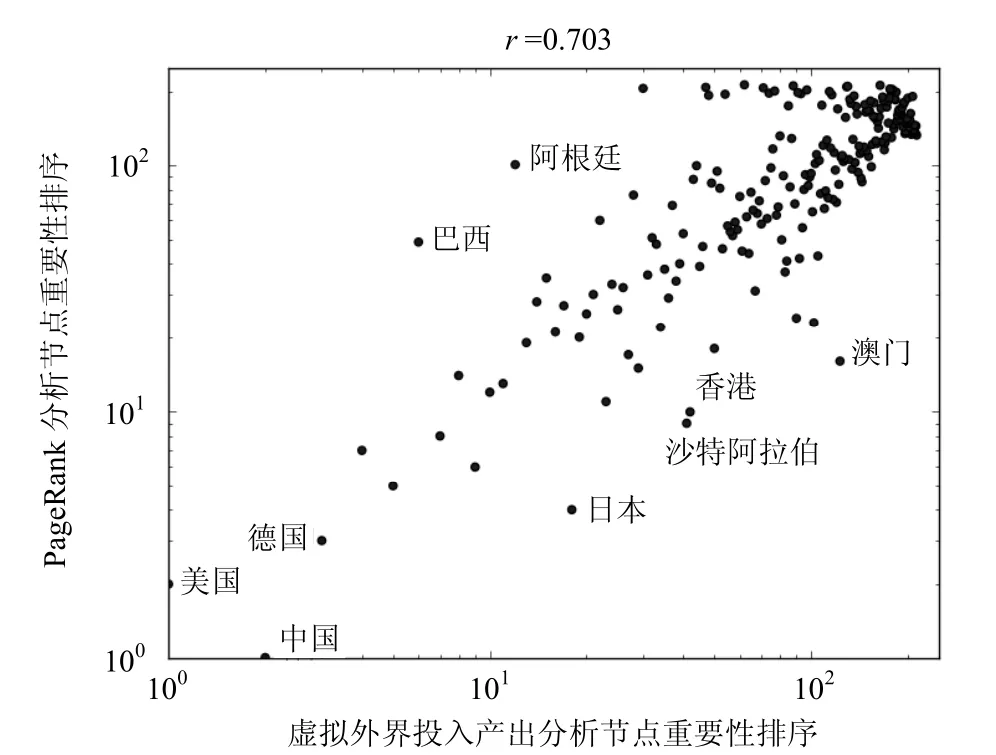
图3 投入产出和PageRank算法得到的贸易网络节点重要性排序对比

4 结束语

本文针对标准的投入产出分析方法不能识别缺乏外界流入流出量的封闭流网络系统节点重要性这一问题，通过在网络中增加虚拟的外界节点将封闭流网络系统转化为开放的流网络系统，实现了一般的流网络中关键节点重要性的评估。本文以中国铁路网络和世界粮农贸易网络的关键节点识别问题为例，演示了虚拟外界投入产出分析法的应用过程与结果，并将这种方法与PageRank方法进行了对比。本文所提出的方法为在社会、生物和技术系统中广泛存在的封闭流网络系统[1-5]的节点重要性评估提供了一种可选的手段。

本文在投入产出分析的虚拟消去法中，假设当一个节点被删去后投入产出系数矩阵B中的元素是不变的，也就是说剩余节点之间的流量分布关系是保持不变的。但在一些实际的流网络系统中，当某个节点被删除后流量可能会进行重新的分配。如何在现有的投入产出分析法中考虑流量重分配效应，是一个需要进一步探讨的问题。

[1]BARRAT A, BARTHELEMY M, PASTOR-SATORRAS R,et al.The architecture of complex weighted networks[J].Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(11): 3747-3752.

[2]GAI P, KAPADIA S.Contagion in financial networks[C]//Proceedings of the Royal Society of London A:Mathematical, Physical and Engineering Sciences.London:The Royal Society, 2010: 2401.

[3]LIN J Y, BAN Y F.Complex network topology of transportation systems[J].Transport Reviews, 2013, 33(6):658-685.

[4]LEICHT E A, CLARKSON G, SHEDDEN K, et al.Large-scale structure of time evolving citation networks[J].The European Physical Journal B-Condensed Matter and Complex Systems, 2007, 59(1): 75-83.

[5]DUNNE J A, WILLIAMS R J, MARTINEZ N D.Food-web structure and network theory: the role of connectance and size[J].Proceedings of the National Academy of Sciences,2002, 99(20): 12917-12922.

[6]LÜ L Y, CHEN D B, REN X L, et al.Vital nodes identification in complex networks[J].Physics Reports,2016, 650: 1-63.

[7]任晓龙, 吕琳媛.网络重要节点排序方法综述[J].科学通报, 2014, 59(13): 1175-1197.REN Xiao-long, LÜ Lin-yuan.Review of ranking nodes in complex networks[J].Chinese Science Bulletin, 2014,59(13): 1175-1197.

[8]刘建国, 任卓明, 郭强, 等.复杂网络中节点重要性排序的研究进展[J].物理学报, 2013, 62(17): 178901-178901.LIU Jian-guo, REN Zhuo-ming, GUO Qiang, et al.Node importance ranking of complex networks[J].Acta Physica Sinica, 2013, 62(17): 178901.

[9]LÜ L Y, ZHOU T, ZHANG Q M, et al.The H-index of a network node and its relation to degree and coreness[J].Nature Communications, 2016, 7: 10168.

[10]KITSAK M, GALLOS L K, HAVLIN S, et al.Identification of influential spreaders in complex networks[J].Nature Physics, 2010, 6(11): 888-893.

[11]FREEMAN L C.A set of measures of centrality based on betweenness[J].Sociometry, 1977, 40(1): 35-41.

[12]SABIDUSSI G.The centrality index of a graph[J].Psychometrika, 1966, 31(4): 581-603.

[13]LEONTIEF W.Input-output economics[M].Oxford:Oxford University Press, 1986.

[14]SHEN Z, YANG L, PEI J, et al.Interrelations among scientific fields and their relative influences revealed by an input-output analysis[J].Journal of Informetrics, 2016,10(1): 82-97.

[15]TEMURSHOEV U.Identifying optimal sector groupings with the hypothetical extraction method[J].Journal of Regional Science, 2010, 50(4): 872-890.

[16]LÜ L Y, ZHANG Y C, CHI H Y, et al.Leaders in social networks, the delicious case[J].Plos One, 2011, 6(6):e21202.

[17]GOLUB G H, VAN LOAN C F.Matrix computations(Vol.3)[M].Baltimore: Johns Hopkins University Press, 2012.

[18]BRIN S, PAGE L.The anatomy of a large-scale hypertextual web search engine[J].Computer Networks and ISDN Systems, 1998, 30(1-7): 107-117.

[19]DE DOMENICO M, NICOSIA V, ARENAS A, et al.Structural reducibility of multilayer networks[J].Nature Communications, 2015, 6: 6864.