引入用户情感的高阶奇异值分解推荐算法研究

郭 强，岳 强，李仁德，刘建国

(1.上海理工大学复杂系统科学研究中心，上海 200093；2.上海财经大学金融科技研究院，上海 200433)

0 引言

1 情感计算

本文使用某在线互联网教育中用户评论的数据集来评估所提出算法的性能。该数据集包含2017年1月至3月间的一共1 324 501条用户评论记录，其中用户评论是指用户在选择过的某一社团刊物(下文简称为社刊)上发表评论，一个用户可以对某一社刊进行多次评论。本文定义上述实证数据为原始数据，在原始数据中不难发现用户会在社刊上发表带有emoji表情的评论，其中单个社刊中含有emoji表情的评论记录数的概率分布如图1所示，其中表示单个社刊中含有emoji表情的评论记录的数量，表示的概率分布函数。

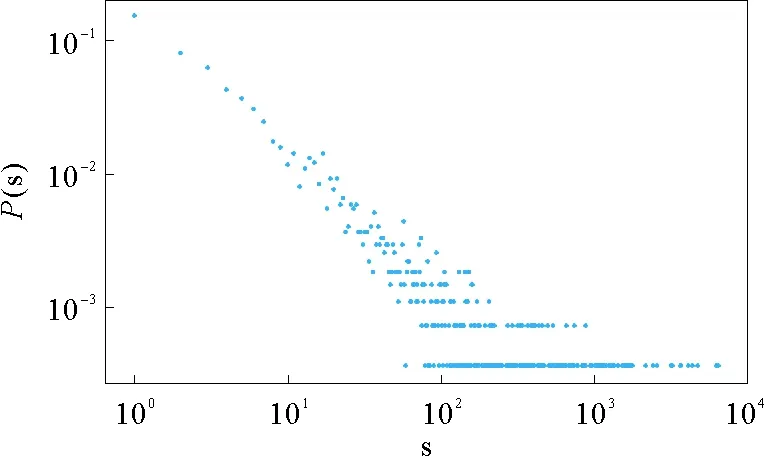
图1 社刊-emoji表情概率分布图

结合图1，经统计可知，即有emoji表情评论记录的社刊占所有全部社刊数量的89%，也就是绝大部分社刊中都有用户发表包含emoji表情的评论记录。

1.1 emoji表情提取

在计算用户情感之前，需要对原始数据进行数据清洗和emoji表情提取。首先删除不含emoji表情的评论记录。其次，结合图2主图可知，用户通常在评论中发表的不同的emoji表情的数量不大于3种，为了防止用户灌水即在一条评论中发很多不同的emoji表情，删除表情种类数大于3种的记录。接下来，结合图2子图可知，极小部分的社刊拥有的用户数小于3个，其中拥有用户数为1的社刊，那唯一一个用户是社刊的创刊者，故考虑到社刊的品质，删除拥有用户数小于3个的社刊记录。

图2 原始数据统计直方图

本文定义原始数据在经过上述3个步骤后，保留下来的数据称为筛选数据。为了获得更稠密的数据，本文在筛选数据上构造了如图3所示的投影网络[22]，即把某一用户评论过某一社刊视作一个新单元节点，若与其他单元节点存在相同的用户或者社刊则产生连边。

如图3所示，用户a在社刊1上评论过，将这条记录看作一个单元节点，用A表示，即A中既包含用户也包含社刊信息。相应的，将用户b和社刊1看作一个单元节点B。因为单元节点A和B中包含同样的社刊1，则A与B之间存在一条连边。以此类推，单元节点之间依靠是否拥有同样的用户或者社刊信息而建立连边，这样便构成了本文使用的投影网络。最后，在投影网络上应用k核分解[23]。实验中k取最大值3 442，便可得到最核心的单元节点。

图3 投影网络构建示意图

图4 数据清洗流程图

表1 实验数据与原始数据对照表

从上述k值最大所对应的单元节点中，保留用户和社刊信息，并定义这部分用户与社刊为核心用户与社刊。再从筛选数据中筛选出包含这部分核心用户与社刊的评论数据即筛选后的评论数据是由核心用户对核心社刊所发表的包含emoji表情的评论数据，本文定义这部分筛选后的数据为实验数据。至此，数据清洗及emoji表情提取工作全部结束，总体流程图如图4所示，其中原始数据和实验数据两者的核心字段变化对比如表1所示。

1.2 情感计算

在本文中，根据用户在相应社刊评论中emoji表情数据提炼出用户情感。大致过程为：首先将emoji表情分成3类，分别是：积极、中立和消极；检验分类结果的一致性；之后给积极、中立和消极分别赋值权重为：1、0和-1，再结合每条记录中3类表情各自出现的频次，如此便可得到某个用户对其选择过的某个社刊的情感。详细用户情感计算过程如下：

经过数据清洗，得到15 370条记录的数据。在这些记录中一共提取出126种emoji表情，并由7名志愿者主观的对这126种emoji表情分成3类，分别是：积极、中立和消极。为了检验志愿者主观分类的结果的一致性，避免出现某个志愿者胡乱分类的情况，本文对分类结果进行了Krippendorff’s alpha检验[24]，检验结果如表2所示。

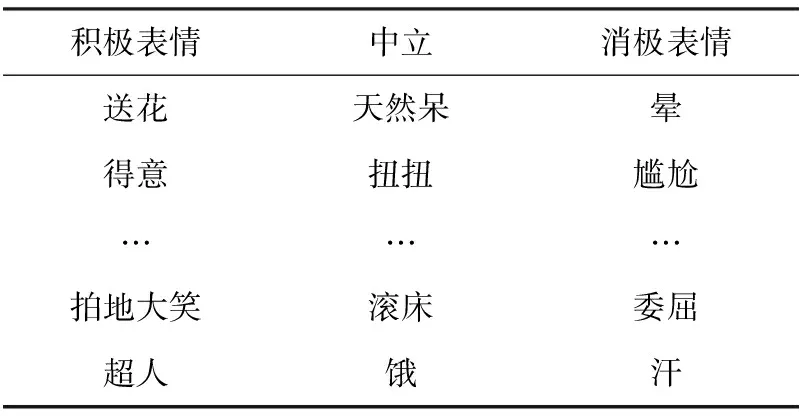
表2 emoji表情分类部分结果

当Alpha值大于基准值0.6时，则表明不同志愿者的分类结果之间的差异是可以被接受的[24]。文中实验的Alpha值为0.706 9大于基准值0.6，所以志愿者的分类结果是可取的。之后，对7名志愿者的分类结果取众数即获得相应emoji表情的所属分类。部分emoji表情分类结果如表2所示。

表情分类结束后，本文根据式(1)来计算用户在某条记录表达对社刊的情感：

(1)

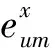
综合某一用户对某一社刊的所有记录，根据式(2)即可得到，总体上用户对社刊的情感：

(2)

其中，n2为用户u对社刊m的所有评论记录数。由式(1)和式(2)可知，用户u对社刊m的情感eum的取值范围是(-1，1)，其中eum=1，即表示用户u对社刊m的评论中全部是积极的emoji表情，透露出用户u对社刊m的称赞、喜爱的情感；反之，eum=-1即表示用户u对社刊m的厌恶的情感。

2 引入用户情感的三阶HOSVD分解算法

本节通过一个实例阐述整个引入用户情感的三阶HOSVD分解算法(下文简称HOSVD(uem)分解算法)流程。实例中用户、社刊以及用户对社刊的情感三者之间的关系如图5所示，其中用户u1和u2对社刊m1的情感为e1，用户u2对社刊m2的情感为e2，用户u3对社刊m2和社刊m3的情感为e3。

2.1 构造初始张量

通过实例中用户、社刊以及用户对社刊的情感三者关系来构造一个三阶张量A∈R3×3×3，并将某个用户对某个社刊的情感这一条记录出现的权重作为张量A的元素。为了避免高维张量导致算法具有高阶时间复杂度，Symeonidis[14]定义了一个稀疏张量即将图5中出现的5条记录的权重全部初始化为1，如表3所示。相应地，图5中没出现的记录的权重全部为0。

图5 实例数据关系图

表3 通过实例中数据构造的初始张量A

图6 实例中的初始张量AFig.6 Original tensor A of instance data

由表3可知，初始张量A中的元素分别是：a111=a211=a222=a332=a333，其余元素的值全部为0。其中，a111=1对应表3中的第一条记录，即u1用户对社刊m1的情感为e1；相反的，以a112=0为例，a112表示用户u1对社刊m2的情感为e1，而这条记录并没有出现在表3中，则a112=0。为了更形象的表示三阶张量A，将张量A写成三维矩阵的形式，如图6所示。

2.2 初始张量n-模展开

为了在三阶张量A上应用奇异值分解(下文简称SVD分解)，首先需要将张量A进行矩阵展开，即将张量A按照n-模重新排列成一个矩阵。三阶张量A的n-模展开示意图如图7所示，其中I1、I2、I3表示三阶张量的三个维度，并且A1∈RI1×I2I3，A2∈RI2×I1I3，A3∈RI1I2×I3。

实例中初始张量A的1-模、2-模和3-模展开的矩阵A1、A2、A3分别表示为

图7 三阶张量A的n-模展开示意图Fig.7 n-mode unfolding of 3rd-tensor

2.3 SVD分解

(3)

SVD分解过程中需要对S矩阵进行调整，以便于过滤掉原始矩阵中的噪声信息。在本文中，将保留原始矩阵中信息量多少定义为信息量阈值σ，即信息量阈值不大于为对角矩阵S中前k大奇异值的和与所有奇异值和的比例。设对角矩阵前k大奇异值的和为pk，所有奇异值和为p，则信息量阈值计算如式(4)所示。

(4)

本文中，为了取得最佳的实验结果，经过多次实验，最终确定在A1、A2、A3上进行SVD分解所取的信息量阈值σ分别是：0.5，0.9，0.5。信息量阈值确定后就可以求k的值。k是满足式(4)的最小整数值。当k值确定后，从对角矩阵S中取出前k大奇异值组建成新的对角矩阵Sk；从U和V中选取相应的前k个左右奇异向量，分别组建成新的Uk和Vk，则降噪后的A1、A2、A3如式(5)所示。

(5)

2.4 计算核心张量

(6)

图8 实例中近似核心张量

2.5 计算近似张量

(7)

为了方便生成推荐列表，将图9中的三维矩阵写成表4的形式。

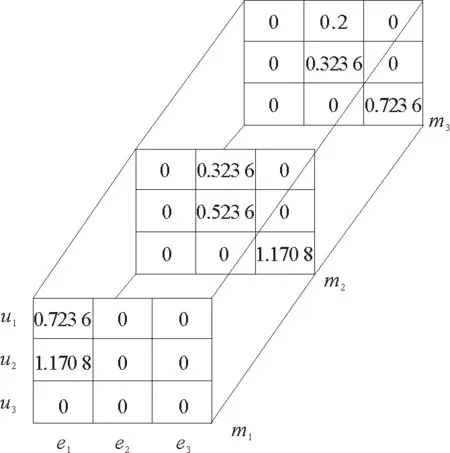
图9 实例中近似张量

表4 实例中计算出的近似张量

2.6 生成推荐列表

3 实验设置与结果

3.1 实验设置

(8)

其中，di(k)表示用户ui在测试集中记录同时出现在推荐列表中前k个位置的记录个数；召回率是出现在在测试集中记录的同时也位于推荐列表前k个位置的记录个数与测试集中所有记录个数Ci的比值。平均所有用户的召回率，得到数据集上所有用户的平均召回率，即为：

(9)

F1值是一种统一准确率和召回率的系统性能评估标准，定义为

(10)

3.2 实验结果

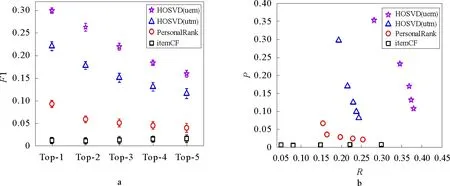
图10 各算法F1值、准确率和召回率结果对比图

表5 各算法F1值的Top1～5的平均值

4 结语

emoji表情已经成为互联网时代必不可少的元素之一，是人们表达情感的重要载体。通过分析海量的emoji表情信息，可以了解用户的情绪状况、对某个社会的现象的观点、对某款产品的喜好等，意义非凡。目前国内外学术界关于emoji表情的研究尚处于起步阶段，但随着emoji表情的蔓延式发展，可以肯定的是对emoji表情的分析与研究是未来的大趋势。对emoji表情的分析不仅可以对人机交互、市场营销等领域产生重要影响，具有十分可观的商业价值；还可以用来分析用户心理、态度等，对维护社会稳定有所帮助。本文只是从用户情感的角度入手，将emoji表情引入到推荐算法中。但因涉及到三阶张量，本文提出的算法的时间复杂度较高，不适用于大规模网络。同时该方法推荐效果依赖评论中emoji表情转化成用户情感的准确性，因此未来的工作可以进一步将文中emoji表情的分类分的更细致，使提炼出的用户情感更精确，从而提高推荐的效果。