基于多传感器系统的光伏并网发电功率预测*
2018-03-26蒋春晓杨柏松
程 泽, 蒋春晓, 杨柏松
(1.天津大学 电气与自动化工程学院,天津 300072; 2.广东石油化工学院,广东 茂名 525000)
0 引 言
光伏(photovoltaic,PV)并网发电在替代常规能源[1~3]方面有着巨大的潜力,但PV发电的决定性因素—辐照度对天气变化十分敏感,受大气环境中温度、湿度、气压以及光伏板自身特点等诸多因素的影响,具有不稳定性、间歇性和随机性等特征,容易造成巨大的经济损失[4,5]。PV并网发电功率预测课题的研究在太阳能应用领域尤为迫切。
国内外现阶段对于PV发电预测方法的研究主要分为直接法和间接法[6]。比较可知,直接法具有精度高,计算负担小,普遍性强,无需对辐照度进行监测,省去了一类方法中的多次建模等优点[7,8]。但使用单一模型预测难免出现过拟合问题。另外,对于我国北方近年来雾霾天气频发的现状,在影响光伏发电的主要气象因素中,还应该包括空气质量指数(air quality index,AQI)和PM2.5等与雾霾相关的气象因素,但雾霾因素往往与其他影响因素有着高度耦合的现象,必须采用多传感器采集海量数据才能保证准确性及预测的稳定性。
本文提出了通过由电流传感器、电压传感器、温度传感器、光照传感器、风速传感器组成的光伏微系统采集环境温度、湿度、大气气压、AQI、PM2.5等对光伏发电量有明显影响效应的大量历史数据,基于逐步选择方法对数据和与雾霾相关的AQI和PM2.5等参数进行变量之间耦合研究,利用更加准确的高斯混合模型代替一般K—means聚类方法对不同天气类型进行聚类,对不同的日类型建立不同的神经网络模型。利用天津大学26教学楼光伏微网系统的2012年上半年到2015年10月份天气参数和发电功率历史数据进行训练,建立模型,在实际的预测中采用模糊数学的方法对天气预报中的各天气条件的语言描述进行推理,选取预测模型进行预测。
1 预测模型建立
1.1 基于逐步选择的变量约减方法
逐步选择(stepwise selection,SS)法每次引入一个变量,检验先前引入变量的判别能力是否因新引入变量而小于阈值,若是,则及时从判别式中剔除,直到判别式中的变量都很显著,且剩余的变量无重要的变量可引入判别式时,逐步筛选结束。首先,假设诸多气象因素在影响PV发电量之间的关系存在着显著的差异,但无论增加或者去掉其中若干个变量后,仍能达到对PV发电量的相同影响效果。
假设已经引入了p-1个变量X1,X2,…,Xp-1,有
(1)
式中p个变量构成的离差矩阵分块
(2)

本文所使用的变量约减方法是运用逐步选择法从原始气象、发电量数据库中发现影响PV发电量的不同气象参数之间的关联,从而得出影响PV发电量的主要影响因素,对非主要影响因素进行剔除约减,降低变量之间的强耦合性。
1.2 发电模型输入变量的组合分析
雾霾天气通常由多种污染源混合作用形成,其严重程度与PM2.5、风速、AQI相关,3个指标同时并不同程度地影响着雾霾标准,并且各指标间存在着很大的耦合性,因此,通过变量约减的方法对以上4个变量进行去耦合,通过不断迭代约减,将最后剩余的一个变量标准作为雾霾的严重程度的标准,能够很好地给出雾霾与发电量之间的影响因子大小。本文选取温度(T)、湿度(H)、大气压(P)、风速(S)、AQI(A)、PM2.5(PM)等参数作为影响PV发电的变量组合。根据以往PV发电预测经验,以上各参数已基本包含了影响PV发电的所有气象指标,但其中不乏若干个变量对光伏发电相同的影响情况,所以,按照以上自然次序依次计算各变量显著度和加入新变量后的显著度,若检验统计量落在不同隶属区间内,本文根据变量约减的经验选取F=4和F=0.8 2个值,按照相应的隶属区间选择变量或者剔除变量,最终得到最佳组合,具体程序流程如图1所示。

图1 逐步选择法的程序流程
利用SPSS工具箱计算结果如表1所示。
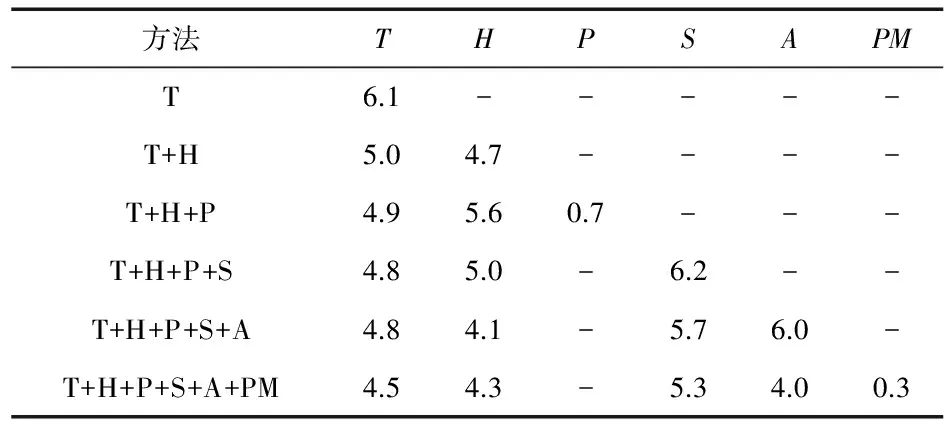
表1 各变量的检验统计量
根据检验统计量的值选择出了温度、湿度、风速、AQI4个变量作为影响发电量的最佳变量组合。
1.3 高斯混合模型的天气类型聚类
采用高斯混合模型[9](Gaussian mixture model,GMM)对约减后的气象数据样本进行天气聚类。在此基础上,对每种天气类型建立不同的人工神经网络模型。高斯混合聚类使用期望最大化(expectation maximization,EM)算法更新群集的中心。
GMM由K个单高斯模型(single Gaussian model,SGM)据不同概率值组成,其中,任意一个单高斯模型为高斯混合模型的一个component,有
(3)
其中
(4)
与K-means方法类似,K值为预先确定的所要寻找的群集数,本文期望对气象数据进行晴天、云天、阴天、雨天、雾霾天5种不同天气类型划分,所以,取K值为5,为d维列向量输入,由于每一类别C均有其自己的均值、方差,将代入式(3),当概率大于一定阈值时,即认为数据样本数据属于C,本文阈值取经验值0.7~0.75。运用此方法对气象数据分时聚类的步骤如下:
1)利用EM算法确定模型中πk,μk,εk参数。
2)从混合模型中选取出第k个component,概率为πk,计算x属于第k个类别的概率;如果大于阈值,即认为x属于k类;如果概率小于阈值,重复步骤(2),直到得到K种不同的天气聚类结果。
本文将历史数据库和K=5值作为高斯混合模型的输入,输出为5种不同的天气聚类结果及相应概率值。
1.4 径向基函数网络
将经变量约减后的历史数据库,在不同的天气聚类结果基础上,分别建立分时径向基函数(radial basis function,RBF)模型,具体的流程如图2所示。

图2 天气聚类结合RBF建立模型
以2012年下半年到2015年10月的历史数据为基础,分不同天气状况进行聚类,分时建立各自的RBF模型,利用以上数据训练确定参数。
1.5 RBF神经网络的结构和训练
将约减后的变量数据进行归一化处理,作为RBF的输入变量,有效减少了神经元饱和的可能性,所用到的RBF的结构如图3所示。

图3 RBF神经网络的各层结构
隐含层采用高斯函数
μj(x)=exp[-(x-cj)2/σ2],j=1,2,…,q
(5)
式中μj(x)为隐含层节点的输出;x=(x1,x2,…,xn)T为输入变量;cj为第j个高斯函数的中心值;σj为第j个高斯函数的尺度因子;q为隐含层节点个数。
2 基于模糊数学的方法选择模型
建立并训练了10∶00~16∶00的每1 h不同天气状况下的35个不同模型,利用模糊数学的方法确定预测时刻模型,使用该模型进行功率预测,获得更好的预测精度。
2.1 模糊规则的基本原理
模糊数学的方法选择模型的阶段框图如图4所示。模糊推理(FF)体形式如下:
Theny1∈Bk

图4 模糊推理选择子模型图解
2.2 模糊推理选择子模型
如图5所示,通过天气预报和中国气象网分别获取天气描述的4个不同的模糊变量输入,温度、湿度、AQI等4个模糊输入变量分别划分为3个模糊域,经模糊化过程,规则评估,去模糊化,最终得到一个清晰的RBF预测子模型。4个模糊输入在不同模糊值情况下,分别触发不同的模糊输出,得到不同的预测子模型,135个不同触发规则所对应的模糊输出如表2所示。
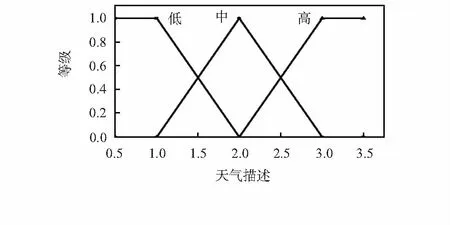
图5 天气预报口头描述天气类型的模糊输入
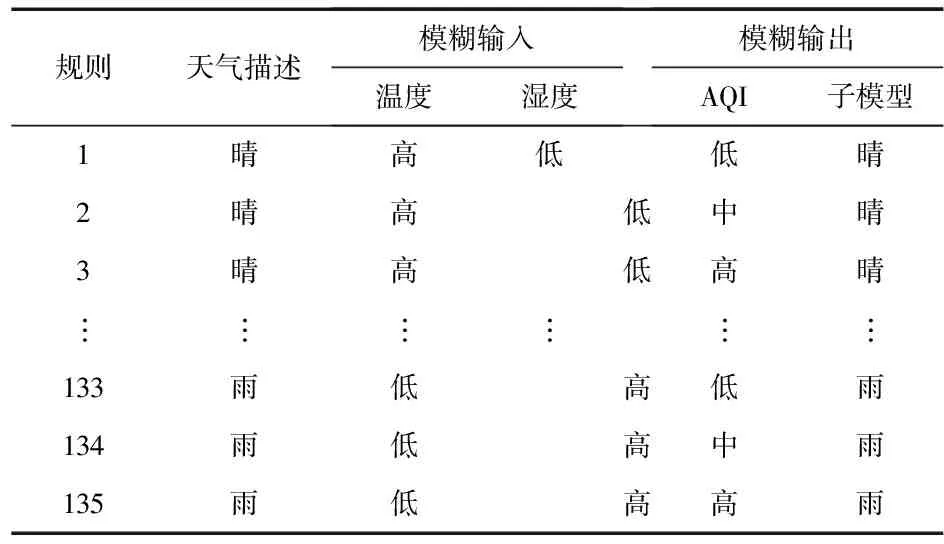
规则天气描述模糊输入温度湿度 模糊输出AQI子模型1晴高低低晴2晴高低中晴3晴高低高晴︙︙︙︙︙︙133雨低高低雨134雨低高中雨135雨低高高雨
如图6所示,模糊输出变量分成4个不同的区域,分别包括了晴、云、阴、雨。利用预测时刻的4个模糊输入变量,预测时刻前一时刻的模糊输入,预测时刻后一时刻的模糊输入分别获得模糊输出值。
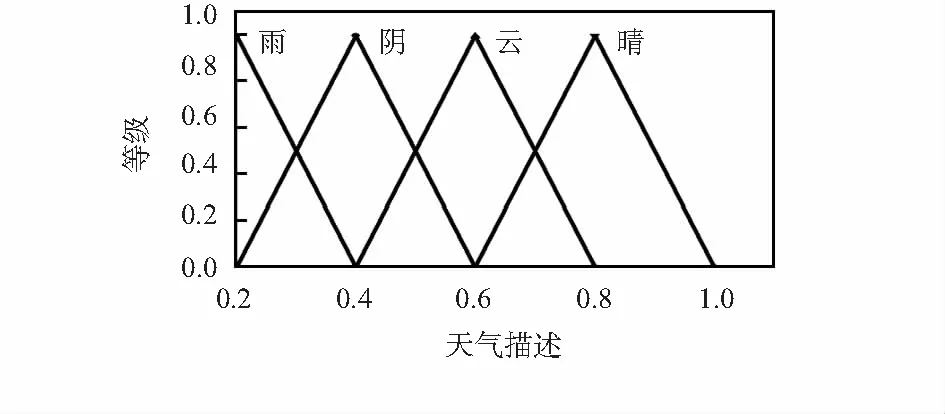
图6 模糊输出变量的4个不同分区
经过重心法获得最终模糊输出值
(6)

3 结果分析
为验证本文提出预测方法的有效性和发电功率的精确度,采用均方根误差(root mean square error,RMSE)和平均绝对百分比误差(mean absolute percentage error,MAPE)如式(7)、式(8)
(7)
(8)
针对天津大学光伏PV微网系统不同天气条件下的日常时刻发电功率进行预测,实验结果误差分析,如表3所示。

表3 不同天气类型的误差比较 %
可以看出:晴天的发电功率预测误差相对于其他天气类型误差较小,由于云天的辐照度波动性较大,对发电量的影响较大,所以在几种不同天气类型下误差最大,但基本能够达到商业预测发电功率的要求。总体来说,运用本文所提的方法在5种不同天气状况下的预测精度聚能达到较高的要求。
为说明本文预测方法与传统一般方法具有较高的精确度,使用方法与其他方法分别进行发电功率预测,并比较实验结果,如表4所示。可以看出:雾霾天下的预测误差相对较好,混合高斯聚类辨析不同天气类型的精度相对较高,逐步选择法筛选出的雾霾指标能够很大程度上代表雾霾对光伏发电量的影响标准。该方法在我国北方天气类型聚类当中亦具有较好的精度。
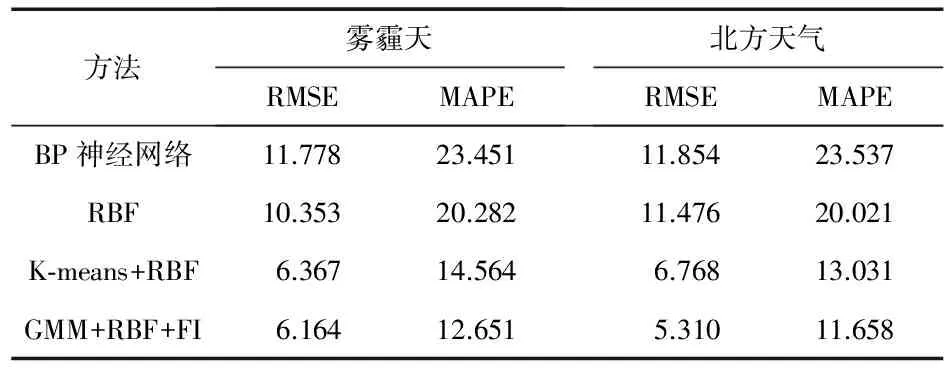
表4 不同预测方法下的误差比较 %
图8为不同预测方法效果比较,可以看到,高斯聚类结合模糊推理的预测方法误差较小,效果较好。

图8 不同预测方法的结果比较
4 结束语
应用逐步选择法、高斯聚类、径向基函数和模糊推理相结合的方法对光伏发电功率进行预测,能够获得更高的预测精度。得到以下结论:
1)针对繁复的气象数据利用逐步选择的方法,筛选出对光伏发电影响的最佳气象因素组合。
2)高斯聚类能够以期望最大化算法更新群集中心结合RBF的方法,相对于其他聚类方法有较好的预测精度。
3)模糊推理选择子模型的方法,能够通过预报天气数据,推理得到预测时刻的天气类型,选择子模型更能反映气象数据和发电量之间的规则,有效性更好。
[1] Femia N,Petrone G,Spagnuolo G,et al.Optimization of perturb and observe maximum power point tracking method[J].IEEE Transactions on Power Electronics,2005,20(4):963-973.
[2] Kim I S,Kim M B,Youn M J.New maximum powerpoint tracker using sliding-mode observer for estimation of solar array current in the grid-connected photovoltaic system[J].IEEE Transactions on Industrial Electronics,2006,53(4):1027-1035.
[3] Xiao W,Lind M G J,Dunford W G,et al.Real-time identification of optimal operating points in photovoltaic power systems[J] .IEEE Transactions on Industrial Electronics,2006,53(4):1017-1026.
[4] Xu R,Chen H,Sun X.Short-term photovoltaic power forecasting with weighted support vector machine[C]∥2012 IEEE Inter-national Conference on Automation and Logistics(ICAL), IEEE,2012:248-253.
[5] 徐 英,吴海涛,张 涛.基于可调恒流源技术的热式气体质量流量计[J].传感器与微系统,2016,35(5):64-66.
[6] Cooke W F,Liousse C,Cachier H,et al.Construction of a 1°*1° fossil fuel emission data set for carbonaceous aerosol and implementation and radiative impact in the ECHAM4 model[J].Journal of Geophysical Research,1999,104:22137-22162.
[7] 颜 鹏,刘桂清,周秀骥,等.上甸子秋冬季雾霾期间气溶胶光学特性[J].应用气象学报,2010,21(3):257-265.
[8] Mei S W,Zhu J Q.Mathematical and control scientific issues of smart grid and its prospects[J] .ACTA Automatica Sinica,2013,39(2):119-131.
[9] 田冠亚,程 佳,李文军,等.150 mL活塞式液体微小流量计量标准装置的研究[J].传感器与微系统,2011,30(12):21-24.
