基于IIW标准的塔式起重机疲劳损伤评估

2018-03-26马思群谢兆聚张鹏程李保鑫赵方雨

建筑机械 2018年3期

马思群，谢兆聚，张鹏程，李保鑫，赵方雨，秦伟

（大连交通大学交通运输工程学院，辽宁大连 116028）

近年来，社会经济的快速发展和基础设施建设规模的不断扩大，高层建筑不断涌现。塔机集便捷高效、操作简便、爬升高度高、回转半径大等特点于一身，使得塔机在工程建设领域中的地位不断提高，应用也越来越广泛。

以某型号自爬升式双面塔机为例，其本身和建筑物相连，随着建筑物的增高，自身也在不断爬升，能较好的满足高层建筑的需要。塔机依靠金属结构承载重量，而其自身一般属于桁架结构，杆件较多，工作任务繁重、工作条件复杂。此外在塔身回转以及风载荷的作用下，塔机会受到各种静、动载荷。大量理论及实践表明，焊缝处为其强度和寿命最薄弱的位置，所以对塔机的焊缝进行合理的疲劳损伤评估，是保证塔机安全运行的重要环节。

1 塔机力学模型

该塔机的主要部件由塔身、固定架、回转机构、主臂、副臂、塔帽、提升卷扬和变幅卷扬等部件组成，占塔机总质量75%以上。这些零部件在塔机工作过程中相互配合，共同承受塔机的工作载荷、冲击载荷、风载荷以及自重等载荷。其基本性能参数如表1所示。

先对塔机的整机结构进行简化，并在SolidWorks中建立塔机的整体力学模型，如图1所示。

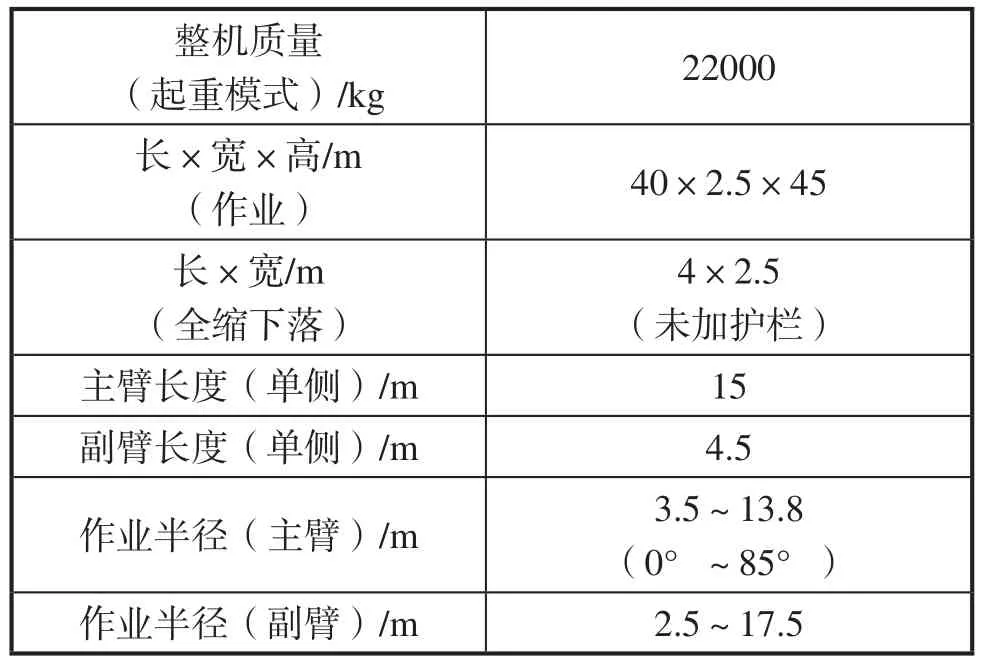
表1 塔式起重机参数表

图1 塔式起重机力学模型

2 塔机有限元模型

2.1 单元类型的建立

将画好的塔机整机力学模型导入Hypermesh中，对部分的圆角、倒角、圆孔进行简化。对其大部分的空间桁架结构，采用梁单元来模拟，箱体结构和加强筋板采用壳单元来模拟，钢丝绳采用LINK80单元模拟。建立塔机模型时各部件所使用的单元类型如表2所示。

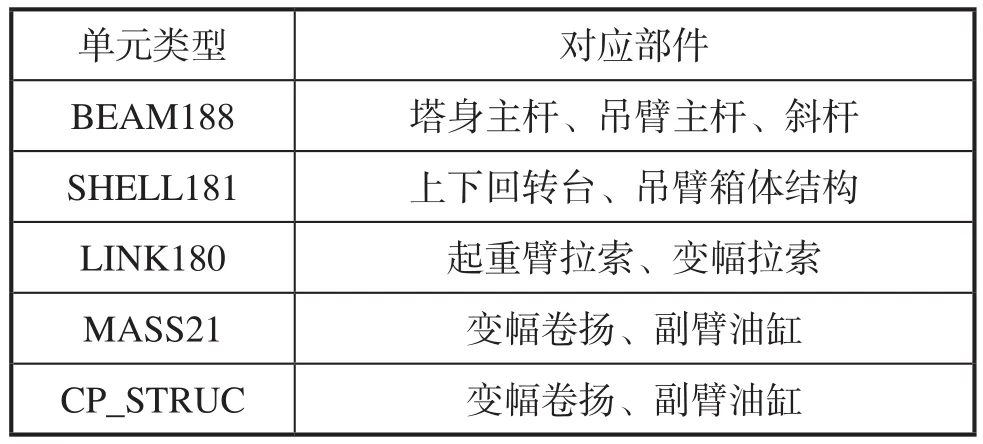
表2 塔机各部位选用的单元类型

在Hypermesh中建立某型号塔机的完整有限元模型，共得到146528个单元、136782个节点，其中壳单元112085个、梁单元34439个、LINK单元4个。建立好的有限元的整体模型和局部模型如图2所示。

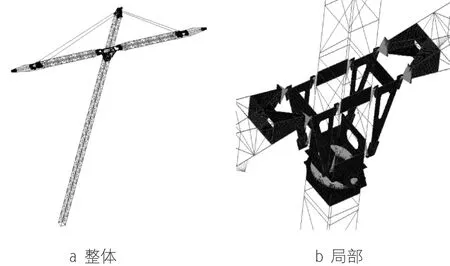
图2 塔机整体和局部有限元模型

2.2 材料选择与属性

在Hypermesh中，定义某型号塔机回转部位和箱体结构钢材料为Q450，屈服应力为450MPa；塔身和吊臂的旋管选用材料为Q390，屈服应力为390MPa。2种钢材料弹性模量均为216GPa，泊松比0.3，密度7800kg/m3。

2.3 塔机工况的建立

2.3.1 约束的建立

塔机底部约束类型为球铰约束，在有限元模型中固定其底部3个方向的移动自由度的约束；而在腰环处约束类型为水平约束，由于模型中X、Z为水平方向，Y为竖直方向，所以载荷应该施加在X、Z方向。

2.3.2 载荷的建立

根据GB/T13752-2017《塔式起重机设计规范》（以下简称为《规范》）可知，塔机在实际进行工作时主要考虑的载荷有：自重载荷、起升载荷、运行变幅回转时的惯性载荷、风载荷及温度载荷［6］。

自重载荷只需要在所建立的工况中添加重力加速度g即可。

起升载荷根据《规范》规定，是通过起升载荷乘以起升动载系数来确定，由该型号塔机的参数可知，其起升速率为0.058m/s，动载荷系数为1.05。

风载根据《规范》规定，塔机正常工作状态的最大计算风压为300Pa；非工作状态下的最大计算风压为800Pa，其目的是为了验算起重机零部件及金属结构的强度、起重机整机抗倾覆稳定性。按照设计规范中的计算方法算的该塔机的迎风面积A=9.5438。

由于该塔机所在的工作环境温度变化不是很大，所以本次计算不考虑温度载荷。

2.3.3 工况的建立

根据相关的企业设计标准，所选用疲劳工况载荷为：

工况一：无吊臂，腰环10m处约束，承受风载荷（非工作状态）；

工况二：吊臂水平，腰环10m处约束，单侧主臂加载2.2t，承受风载荷；

工况三：吊臂水平，腰环10m处约束，一侧加载2.8t，另一侧加载3.0t，承受风载荷；

工况四：单侧吊臂上扬60°，腰环10m处约束，上扬侧主臂加载3.0t，承受风载荷；

工况五：双侧吊臂上扬60°，腰环10m处约束，双侧同时加载3.2t；

以上各工况塔机底部均有球铰约束，且风载荷的方向指向加载侧或加载较大的一侧。

查阅了相关资料并现场与工程技术人员进行了交流，获取了塔机在实际运行当中，各疲劳工况在塔机实际运行过程中所占的比例，如表3所示。

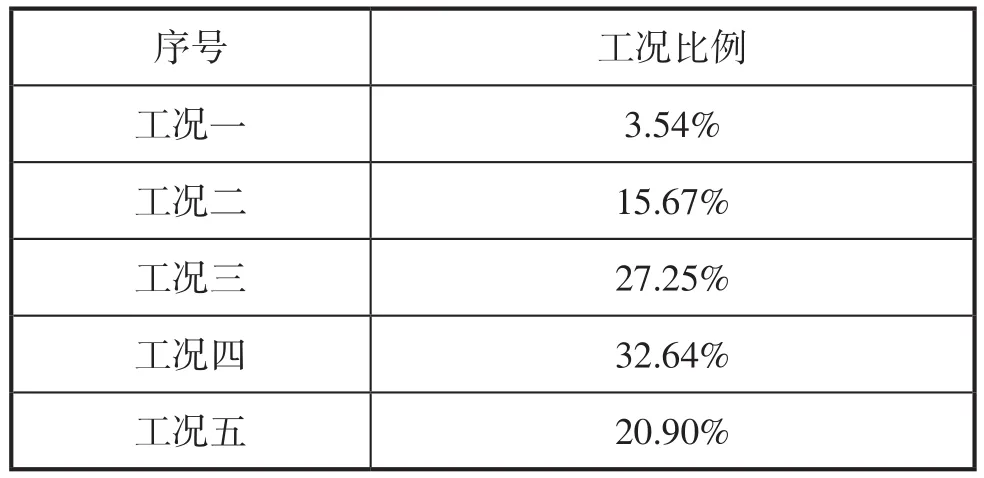
表3 塔机不同疲劳强度统计占比

2.4 有限元静态分析结果

将建立好工况的塔机有限元模型导入到ANSYA中求解计算，得到塔机其各疲

劳工况下的应力和位移云图，只截取应力和位移比较大的工况，如下图3所示。其它工况的计算结果统计如表4所示。

图3 疲劳工况下塔机最大应力和位移云图（部分）

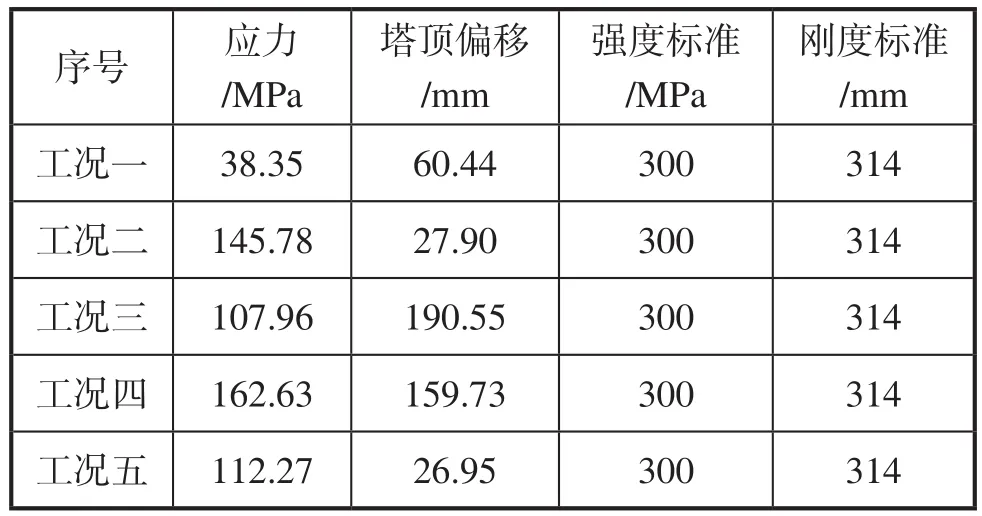
表4 不同疲劳工况下塔机应力最大值及塔顶横向偏移量

由塔机疲劳寿命云图可知：

（1）塔机在回转支座的位置局部应力较大，特别是回转上支座与起重臂的焊缝位置及平衡臂铰接处。

（2）塔机在塔帽位置处应力集中比较明显，且在多个工况下出现的位置基本吻合，最大应力都出现塔帽的几条焊缝处。

（3）塔机工况二和工况三下在主臂和副臂的连接处位移变化明显。

由表4可知，塔机在工况四下的应力较大，为162.63MPa；在工况三的位移较大，为190.55mm，且都比标准值小。而塔机在其他各疲劳工况下的应力和位移值均比所对应的强度和刚度标准值低，所以满足塔机满足不同疲劳工况下的强度和刚度要求。

3 塔机载荷谱的处理

塔机实际工作状态所受的载荷是随机且复杂的交变载荷，所以载荷谱的获取和处理影响到塔机疲劳寿命预测的准确性。本次实验采用现场贴片以获取塔机实际工况的应力时间历程，本次选取的测点应能体现塔机在不同运行工况下整体受力的关键位置，基于之前疲劳工况强度分析结果以及设计经验，本次测试实验选取了5个测点作为主要测试点，具体位置如图4所示。

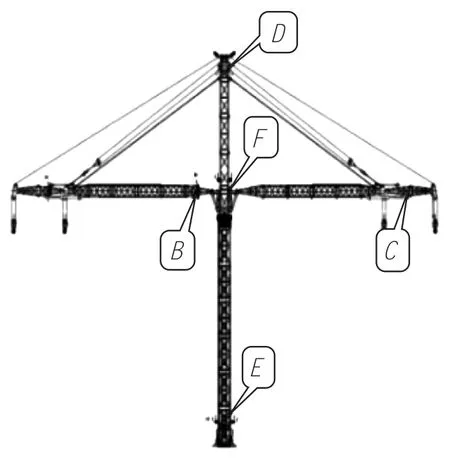
图4 塔机应力测点位置示意图

3.1 应力谱处理方法

对实际测得应变时间历程，进行应变转化成应力、去零飘、去毛刺、滤波（低通滤波）等过程处理，对滤波后的应力时间历程的数据用雨流计数法进行处理，并得到相应工况下的雨流计数直方图，由于篇幅有限，本文只列举工况五下的载荷谱和雨流计数分布直方图，如图5所示。

图5 塔机在工况五应力载荷谱和雨流计数分布直方图

3.2 应力谱编制

同理以塔机工况五为例，对不同工况下的实测的应力时间历程，通过雨流计数对载荷谱进行编制，得到用于塔机焊缝疲劳寿命评估的动应力谱。根据以往的经验和塔机的实际应用情况，需要有一定的安全裕度，本文中所取的应力谱编制均为8级。工况五的8级谱如表5所示。

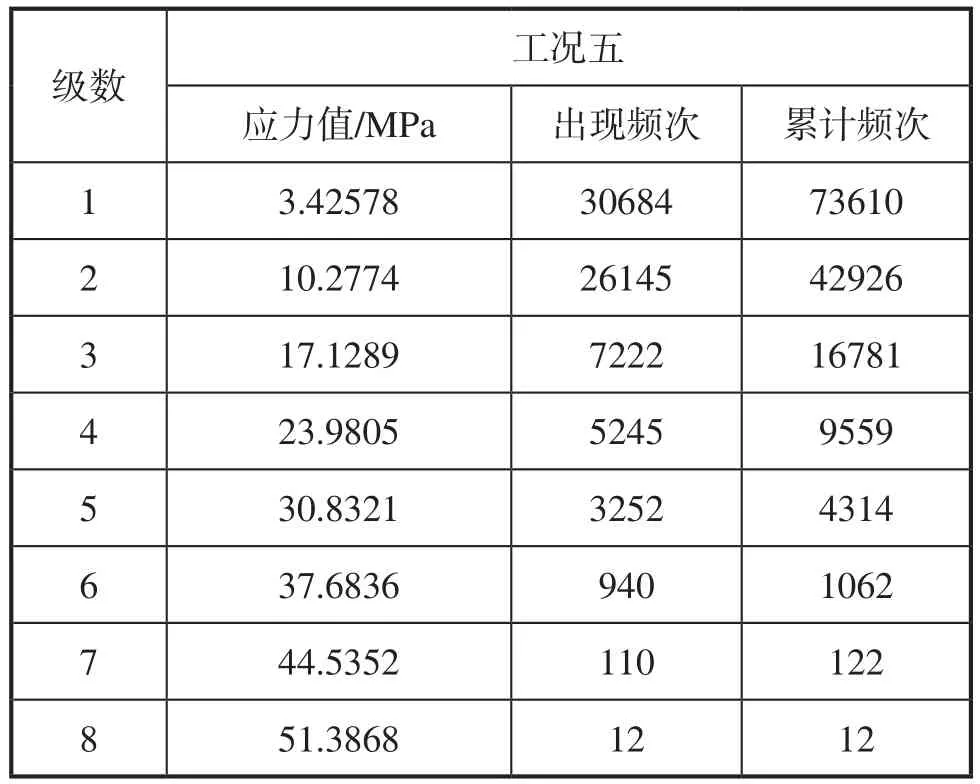
表5 工况五的8级动应力谱

3.3 载荷谱按里程外推

实验所测得到的塔机疲劳载荷谱只是塔机整个使用寿命中很小的一部分，所以在对载荷谱编制过程中需要对其测试统计的载荷谱外推以得到足够多的幅值和载荷频次。如果按照传统的方法对获得的载荷谱外推，只是单纯按载荷频数以比例的形式增加，从而使得塔机的载荷按照测得的载荷频数比例无线循环，其公式为

式中 Flife——外推后的载荷频次矩阵；

F1—— 实际测得塔机外推前的载荷频次矩阵；

M——扩展倍。

按上述公式外推，原来测得的数据会有规律的出现，而此方法会忽略实际工况中出现的最大应力值，塔机的疲劳破坏或寿命受最大值的影响较大，所以外推的结果与实际值有很大的误差。塔机在工作过程中会受到各种因素的影响，综合考虑各种因素外推，得到矩阵

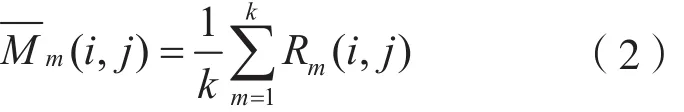
式中 m——塔机实际的工况频数；

i，j——塔机载荷的工作级别；

Rm（i，j）——塔机工况频数矩阵。

对工况五下的载荷谱进行外推，外推周期为40倍，即得到塔机在1年内的载荷谱。外推后的载荷谱结果图如6所示。

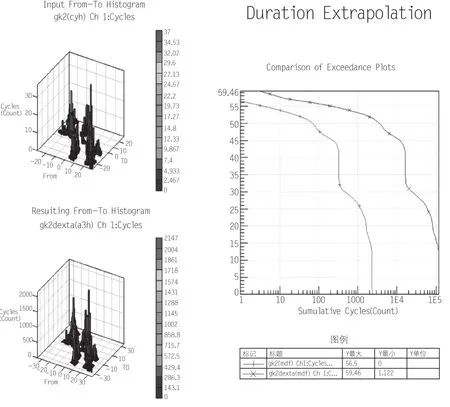
图6 载荷谱按里程进行外推图

从图6可以看出，外推后的载荷谱载荷频次增加到1E5次，而且其幅值也有所增加，这与塔机随时间推移的实际工况相一致。

4基于IIW标准的塔机疲劳分析

本文基于Miner准则和IIW标准，对塔机实测应力谱进行疲劳累积损伤及寿命预测，为塔机的稳定性分析和结构优化提供理论依据。塔机疲劳性能评定步骤如图7所示。

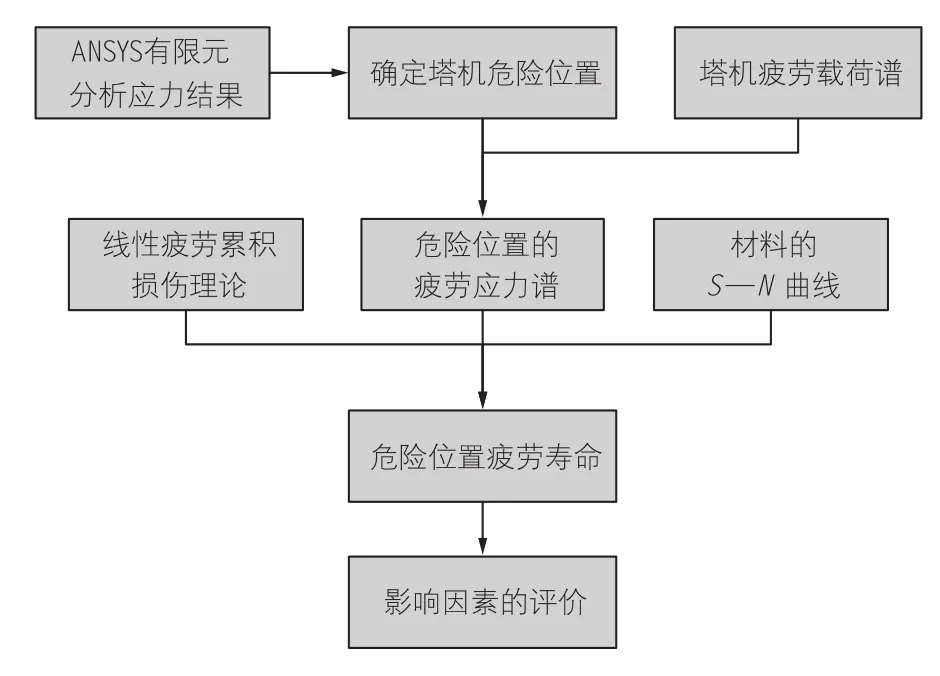
图7名义应力法分析塔机疲劳寿命的步骤

根据前面疲劳强度计算分析结果，取塔机关键部位的4条不同的焊缝类型进行疲劳寿命预测，焊缝的位置如图8所示。查阅文献确定相应的接头类型和对应的FAT值，如表6所示。

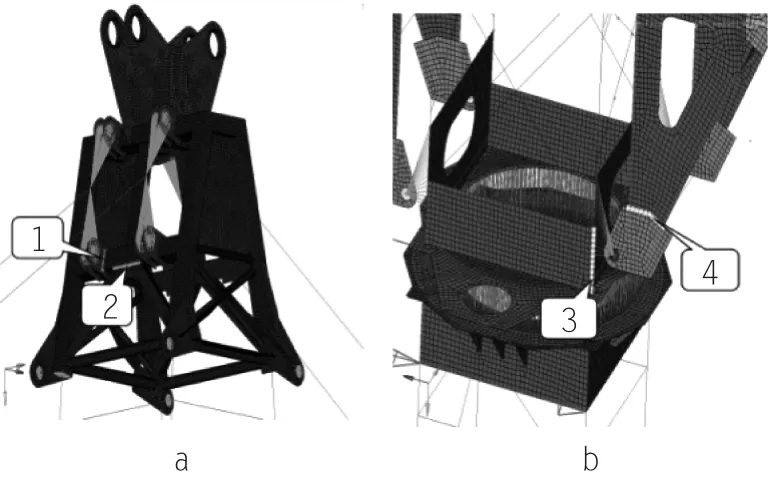
图8塔机焊缝位置图

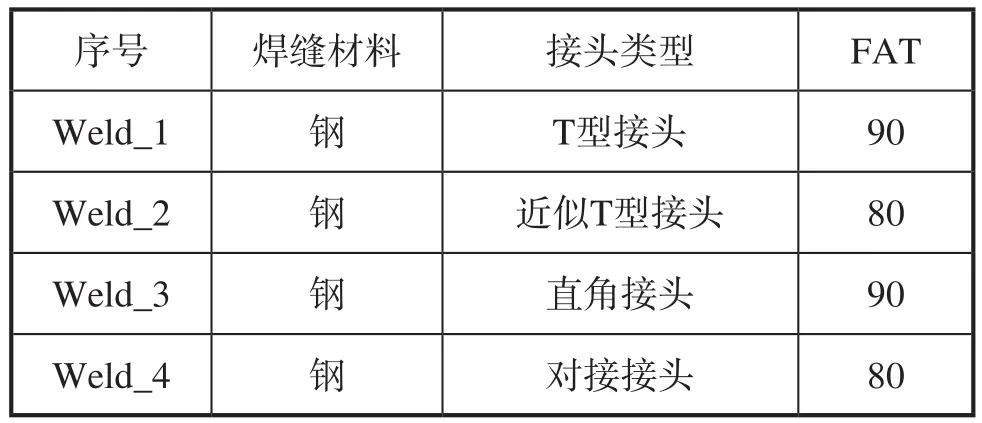
表6 塔机焊缝的位置和对应FAT值

线性疲劳损伤理论是指在不同载荷作用下，各部分的累积损伤值可以线性叠加，不同的应力循环互不干扰或相互独立，当累积损伤达到一定限值时，该零部件就会发生疲劳破坏。

Miner法则的表达式为

载荷在施加过程中，假设试样的载荷循环包括σ1，σ2，σ3，...，σi共i个不同的应力水平，不同应力水平对应的计算疲劳寿命依次为N1，N2，N3，...，Ni，各应力水平的实际循环数依次为n1，n2，23，...，ni，那么材料总的疲劳累积损伤为：

当损伤D=1时，试样发生疲劳破坏。

当把临界损伤和设为一个不等于1（即临界累积损伤值可能大于1，也可能小于1）的其它常数时，称为修正Miner准则。本文疲劳累积损伤过程符合Miner线性累积损伤法则，计算中认为α=1。

基于IIW标准对该塔机焊接部件进行疲劳寿命分析技术路线具体如下：

（1）确定构件结构疲劳部位，即容易产生疲劳裂纹扩展并致使结构不能正常运行的位置；

（2）如果能够测得构件疲劳损伤位置的动应力谱，那么可以通过雨流计数编制出该测点所对应的应力范围谱；

（3）根据预测点应力类别、焊接接头类型细节及所受载荷方向，在IIW中选择对应的用于建立S-N曲线的疲劳级别（FAT）及相关参数；

（4）根据Palmgren-Miner法则计算损伤比累积。

IIW疲劳损伤计算公式为

则第i级应力水平对结构构成的损伤为

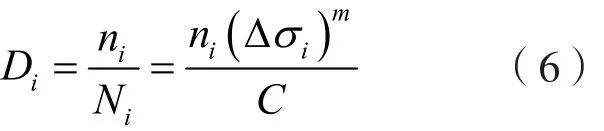
应力谱对结构构成的累积损伤比为

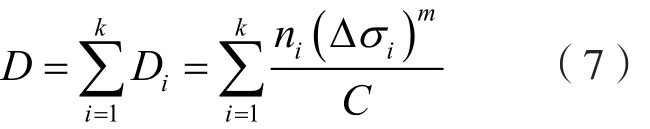
式中 C和m——材料S—N曲线参数；

ni——应力谱第i级应力水平的循环次数；

k——应力谱离散级数，本文取8级；

Δσi——应力谱第i级应力水平的应力范围。

根据表6中不同焊缝类型的FAT值，以及每个工况下所测试的8级动应力谱，结合IIW标准中典型的双斜率S-N曲线，确定每条焊缝所对应的C和m值。再根据公式可分别计算出塔机每条焊缝在不同工况下所对应的疲劳累积损伤，并经过换算得到塔机在不同工况下疲劳寿命，如表7所示。

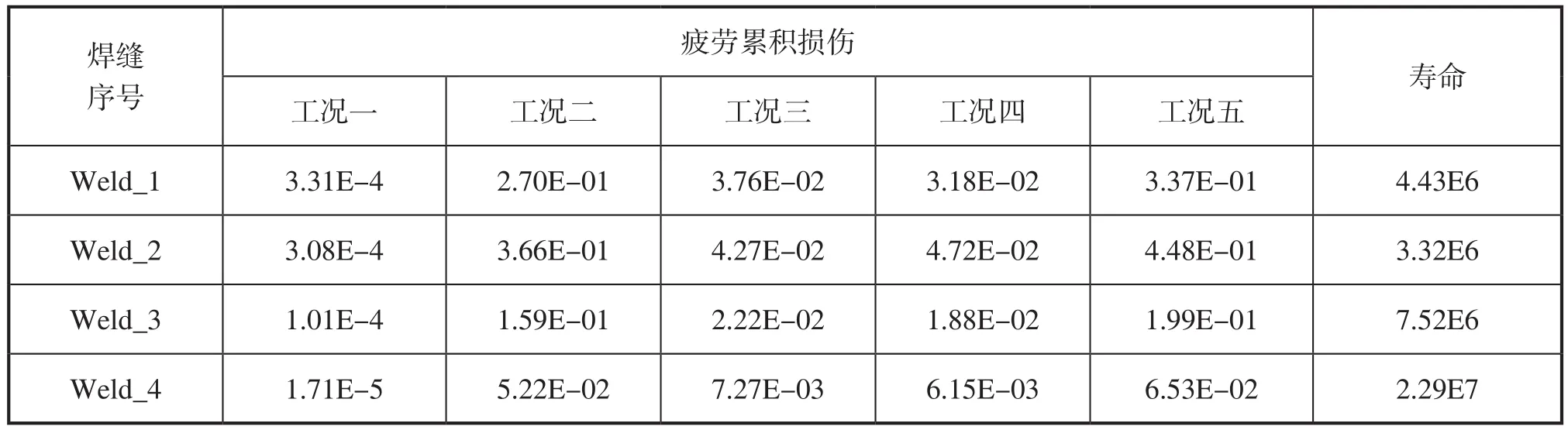
表7 塔机在不同工况下疲劳寿命

塔吊设计寿命为20年，预计每年工作时间为300天，每天工作9h，每小时起吊25次，那么需要经历的载荷循环次数为n=20×300×9×25=1.35E6次，对照上表可知，在Weld_2处疲劳寿命最小，但仍满足疲劳寿命设计要求，且其它焊缝的疲劳寿命也都远远大于计算的循环次数。因此，可认为该塔机设计满足疲劳设计的要求。