基于分段分区聚合近似和模糊聚类的风电出力特性分析

2018-03-25徐邦恩

水力发电 2018年12期

蔺红，徐邦恩

(新疆大学电气工程学院，新疆乌鲁木齐 830047)

随着风力发电技术的发展，风电装机容量在电网中所占比逐日俱增，风电出力具有间歇性和随机性及与负荷需求不同步、反调峰的特点，风电大规模并网对电网产生的影响也越来越明显，需要对风电场出力典型特性进行研究，为电力系统实时调度、调度计划安排、风电场规划及系统备用配置提供技术参考。

随着国内外风电数据信息的搜集、整理、分析工作的展开，许多学者从多角度构建反映风电运行特性指标体系研究风电出力特性。文献[1]构建了多时空尺度的风电特性评价指标体系；文献[2]引入指标体系的时段属性概念，提出面向系统运行的风电出力特性指标体系；文献[3]针对风电功率自身变化特性，定义了平稳性指标评价风电功率的波动程度，实现了风电功率变化特性的量化评估；文献[4]定量计算分析了风电出力的平滑效应；文献[5]从风电出力波动性、相关性、同时率方面，研究了各特性的计算指标及其时空变化规律。但针对提取风电出力典型特性曲线/区间带的研究还较少。

文献[6]从负荷曲线形态出发，提出基于云模型和模糊聚类算法的电力负荷模式提取方法。模糊聚类算法在电力负荷特性分类、电网故障诊断、暂态稳定机组分群等领域有较好的应用[7-9]。模糊聚类算法自身具有缺点[10]，需要事先给定聚类数目，对初始聚类中心敏感、容易陷入局部最优，许多学者对其不足进行了研究，文献[11]提出一种自适应FCM算法；文献[12]针对模糊聚类存在聚类数需要人为指定，不能自适应地进行聚类的缺点提出一种基于局部搜索的自适应核模糊聚类算法；为了提高计算速度，获得较高的聚类性能，文献[13]提出一种基于改进粒子群与模糊c-means的模糊聚类算法。以上算法的改进在一定程度上克服了模糊聚类算法对初始聚类中心敏感的问题，但均需多次迭代计算来确定聚类数目。

本文采用表征多时空尺度的风电波动性、同时率评价指标对风电出力数据进行归一化处理，分段聚合降低维度；对分段后的风电出力数据集，提出模糊聚类算法改进方法，建立自适应函数α(c)，快速地确定最佳聚类数c，对风电出力类型分类；引入变异离散度系数βi，剔除风电出力畸变数据；提出分区加权中位值法，辨识并提取风电出力特性概率区间带。针对新疆区域电网2015年1月份的风电出力数据仿真验证了本文所提方法的有效性及可行性。本文方法具有普及型，可以应用于多空间尺度(风电场或风电基地)及多时间尺度(月、季度或年)风电出力特性的分析计算，提取多时空尺度的风电出力特性概率区间带。

1 改进的自适应模糊聚类算法

1.1 模糊聚类法

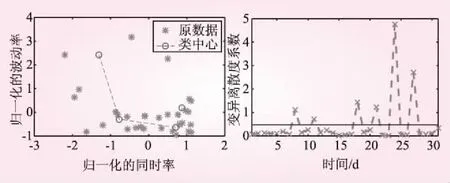
给定的有限数据对象集合X={x1,x2,…,xn},xi∈Rs,数据集合中每个样本是s维向量，把数据对象X聚合成c(2≤c≤n)类，各聚类中心向量矩阵V=(v1,v2,…,vc)，vj∈Rs(1

(1)

式中，q∈{1,+∞}称为模糊权重因子，控制分类隶属度矩阵的模糊度，q越大，分类的模糊度越高。隶属度U(k)、聚类中心矩阵V(k+1)计算公式为

(2)

(3)

1.2 改进的模糊聚类法

模糊聚类算法对给定的数据集进行聚类分析时，关键是最佳聚类数c的选取和模糊权重因子q的确定。

1.2.1 最佳聚类数c的选取

(4)

1.2.2 模糊权重因子q的优选

模糊权重因子值的选取直接决定分类结果的模糊性，数据集的划分尽可能分明，聚类结果不能太模糊，即划分模糊度不能太高。Pal等人则从聚类有效性试验研究中得到q的最佳选取区间为[1.5，2.5]，本文取q=2。

1.3 变异离散度系数

变异离散度系数值βi较大的样本数据说明是与数据特性具有弱相关性或者无相关的数据，将此数据样本删除，第i个样本的变异离散度系数定义为：

(5)

式中，QF(ai)为变异系数倒数表征不稳定性；QP(ai)为模糊离散度表征与聚类中心的远近；Di,k=|(ui,j)2(di,j)2-(uk,j)2(dk,j)2|；ui,j是第j类中第i个元素隶属度；di,j是第j类中第i个元素到该聚类中心距离；σ为模糊距离标准差；Di,k为样本i与其他样本k模糊距离。

畸变数据存在会导致模糊距离和模糊离散度增大，从而根据计算的βi值可以检测出畸变样本数据。

2 分段分区聚合近似

2.1 分区加权中位值法

风电出力是一种偏态分布，绝大多数时刻风电出力偏低，极端数据(如满发出力)会使平均数出现一定程度失真。中位值不易受到极端数据的影响，本文提出的分区加权中位值法更能准确表征风电出力典型特性。分区加权中位值的概率统计法的思路是：将各天j时刻风电出力数据点按总采样数的1/3或1/4来划分区间，先计算出各区间的中位值，再统计各出力数据点落在各区间的概率，以此概率作为中位值的权值，叠加各区间概率加权后的中位值，即为提取的j时刻风电出力典型特性点，分区加权中位值法表示为

(9)

式中，Median(pw,i,max,pw,i,min)为第i区间采样点的中位值；N为区间数；pw,i,max为i区间采样点的最大值；pw,i,min为i区间采样点的最小值；pri,j为采样点分布在i区间内的概率。

2.2 风电出力特性概率区间带

由于风电出力波动性及随机性强，用一条曲线无法表征一个月或一个季度的风电出力特性，采用本文提出的分区加权中位值法，首先计算j采样点的风电出力值pw,j与特性点值pc,j的差值，记为pw-c,j=pw,j-pc,j(下称差值)，差值有正有负，再计算j采样点风电出力特性概率值，确定区间带的上界pup,j和下界pdown,j，获得j采样点的出力特性区间带，依次计算出1到288个采样点(5 min间隔采样，一天有288个采样点)的特性区间带，就得到了风电出力特性区间带。

j采样点风电出力特性区间带上界pup,j和下界pdown,i为

(10)

(11)

2.3 分段分区聚合近似和自适应模糊聚类算法步骤

(1)基于风电出力样本数据，计算风电出力波动性及同时率，对其进行归一化处理。

(2)依据国网公司电价表的峰平谷时段，对风电出力分段聚合降维处理。

(4)按公式(4)计算自适应函数a(c)，返回c，如果c

(5)根据最佳模糊聚类数c，由1.3节的方法计算样本数据的模糊离散度及变异系数倒数，按公式(5)计算出样本数据的变异离散度系数βi。

(7)对删除畸变数据后的风电出力，采用本文提出的分区加权中位值法，即按2.1节方法计算各采样点特性点，获得风电出力特性曲线。

(8)根据2.2节方法计算获得风电出力特性区间带。

3 算例分析

新疆地区冬季时间长，冬季供热负荷大、供热机组多，调峰灵活性差，弃风严重。本文针对新疆达坂城地区2015年1月份风电出力数据，以5 min为一个采样点，共计8 928个数据样本，应用MATLAB软件仿真分析风电出力特性。

3.1 分段模糊聚类近似

负荷波动性具有较强的峰平谷规律性，根据国家电网公司新疆电力公司公布的乌鲁木齐最新电价表中的峰平谷时段，如表1所示，将风电出力按负荷的时段划分为5个时间段。低谷时间段00∶30～8∶30，平段时间段08∶30～10∶00及13∶00～19∶30，高峰时间段10∶00～13∶00及19∶30～00∶30。

图1 负荷峰段时风电出力聚类分布及各天变异离散度系数

按风电的同时率及波动率对风电出力进行归一化处理，再进行分段聚合降维近似，对各段的聚类数c初值选为2，计算自适应函数α(c)，返回各时段的最优聚类数：峰段最优聚类数为5、谷段最优聚类数为4、平段最优聚类数为2和5。风电出力在各峰段、谷段及平段的聚类分布及变异离散度系数如图1、2、3所示，依据变异离散度系数可确定畸变数据。