一类具有非线性发生率的非自治SEIQR模型

李冬梅　郭美静　董在飞　YUE Wu

摘要：考虑了疾病流行期间移民输入和接种、隔离对疾病的控制影响，建立了一类具有非线性发生率的非自治 SEIQR模型，给出模型一致持久性和稳定周期解存在的充分条件。应用模型结果数值模拟分析了隔离对手足口病发病控制的作用。

关键词：非自治；一致持久；周期解；模型的应用

DOI：10.15938/j.jhust.2018.01.027

中图分类号： O175.3

文献标志码： A

文章编号： 1007-2683（2018）01-0148-07

Abstract：Considering the influence of disease control with immigration input， vaccination and isolation during the disease epidemic， we set up a kind of nonautonomous SEIQR model with nonlinear incidence rate. Some sufficient conditions of consistent persistence and stability of the periodic solution of the model are given. The effect of isolation on the control of hand， foot and mouth disease is analyzed by numerical simulations the application of the model solution.

Keywords：nonautonomous， consistent persistence， periodic solution， application of the model

0引言

傳染病每次到来都会对人类的健康造成危害，许多传染病的发病与季节有关，如流感，风疹等疾病。在发病期间，染病者与潜伏者的输入，会引起疾病的蔓延，人们会采取接种疫苗、隔离和治疗等常见手段进行预防疾病的爆发和流行。考虑到疾病季节性的周期变化的关系，许多学者借助非自治传染病模型从理论上来研究防控方法对疾病控制作用，预测传染病的传播规律[1-3]。如下面具有双线性发生率的非自治SEIR传染病模型解的正性、疾病的持久性，周期解的存在性及稳定性研究疾病的发展规律[4-5]。

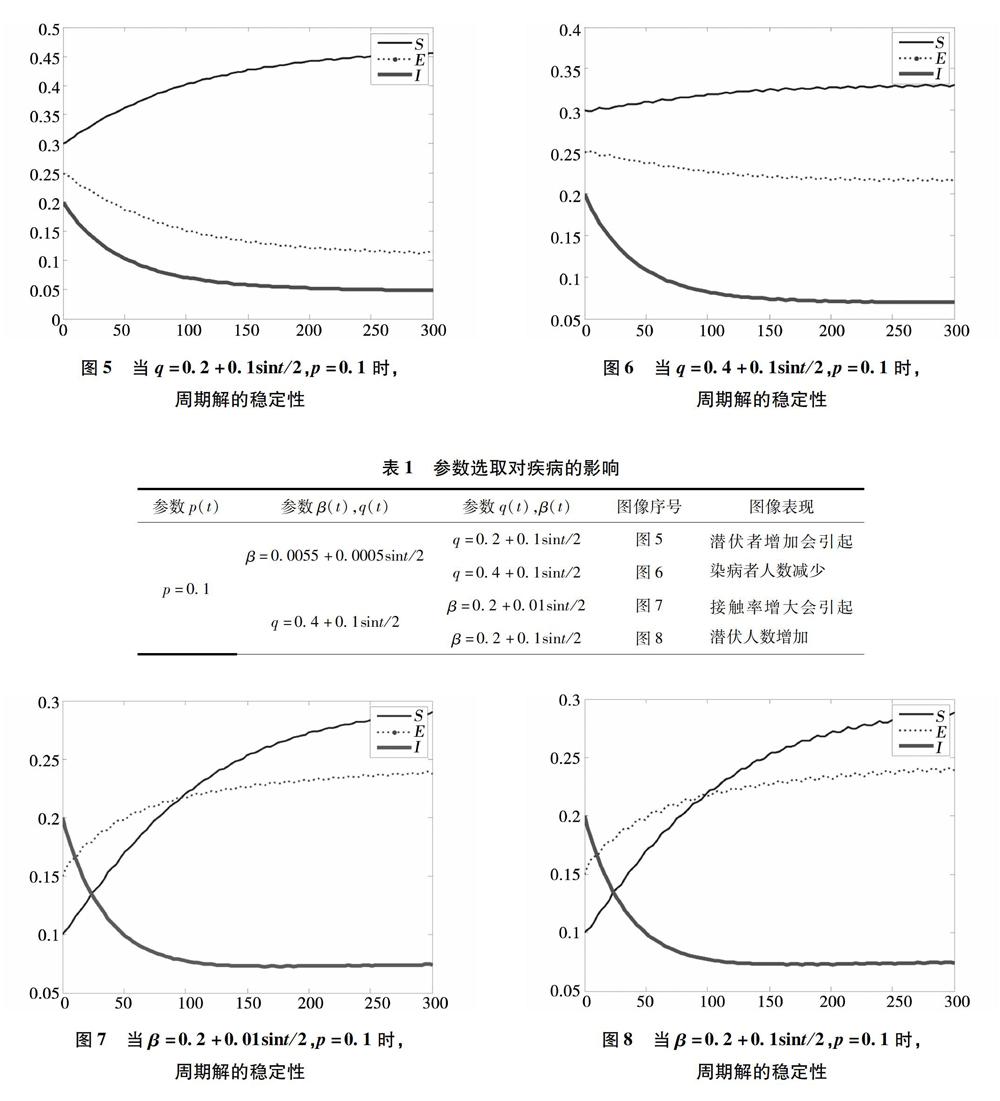
由于选取的各系数较小，并有出现明显的波动形态。但是对比图5和6可以发现：当潜伏者输入波动降低时，易感者人群数增加，潜伏者人群和染病者人群都减少，有利于疾病流行的控制。

对比图7和8可以发现：虽然最后易感者、潜伏者和患病者最终趋近的数值相同，但是图8在趋近的过程中波动较为明显，由于接触率的增加会蔓延到染病者的增加，最终会导致疾病的流行，不利于疾病的控制。

在手足口病发病期间，为防止病情的进一步发展，应减少重症病例的出现；加强检查，降低由潜伏者向患病者的转移率；加强疫情监测和疫情报告工作，及时发现病例并采取消毒隔离等防控措施；开展针对性的大众健康教育活动，提高防病意识，让群众掌握并落实相关的预防控制措施，增强基层医疗单位对手足口病的诊断和救治能力，加强对聚集场所的卫生管理，防止聚集性病例和爆发疫情的发生。

参 考 文 献：

[1]EISheikh MM A， EIMarouf S A A. Global Analysis of an Epidemic Model with General Incidence Rate[J].Journal of American Science， 2010， 6（11）： 770-783.

[2]TENG Z，LIU Y，ZHANG L. Persistence and Extinction of Disease in Nonautonomous SIRS Epidemic Models with Diseaseinduced Mortality[J].Nonlinear Anal，2008，69：2599-2614.

[3]LIU J，ZHANG T. Analysis of a Nonautonomous Epidemic Model with Density Dependent Birth Rate[J].Applied Mathematical Modelling，2010，34：866-877.

[4]李冬梅， 桂春羽， 方健. 潜伏期带有输入的非自治SEIR传染病模型[J]. 哈尔滨理工大学学报， 2013， 18（2）： 126-130.

[5]丁玲芬， 李建利. 一类具有垂直传染非自治的SEIR传染病模型[J]. 云南大学学报（自然科学版）， 2008， 30（2）： 139-143.

[6]马知恩， 周义仓.常微分方程定性与稳定性方法[M]. 北京： 科技出版社， 2001.

[7]杨俊仙，徐 丽.一类具非线性发生率的SIQS传染病模型的动力学性态分析[J].浙江大学学报（理学版）.2015，42（3）：271-275.

[8]BERETTA E， BREDA D. An SEIR Epidemic Model with Constant Latency Time and Infectious Period[J]. Mathematical Biosciences and Engineering， 2011，8（4）： 931-952.

[9]KOROBEINKOV A， MAINI P K. Nonlinear Incidence and Stability of Infectious Disease Models[J]. Mathematical Medicine and Biology， 2005， 22（2）： 113-128.

[10]宋修朝，李建全，杨亚莉.一类具有非线性发生率的SEIR传染病模型的全局稳定性分析[J].工程数学学报，2016，33（2）：175-183.

[11]宋燕， 庞天舒. 具有常数输入及非线性发生率的SIQR传染病模型[J]. 生物数学学报， 2013， 28（3）： 454-460.

[12]LI M Y，MULDOWNEY J S. Global Stability for the SEIR Model in Epidemiology[J]. Mathematical Bioscience，1995， 125（2）： 155-164.

[13]LIU W M，HETHCOTE H W， Levin S A. Dynamical Behaviour of Epidemiological Models with Nonlinearincidence Rates[J]. Journal of Mathematical Biology， 1987， 25（4）： 359-380.

[14]王娟，韓欲清，李学志.一类具有非线性发生率的传染病模型的稳定性[J].数学的实践与认识，2012，42（12）：112-117.

[15]李桂花，白京.一类具有非线性发生率和治疗函数的传染病模型研究[J].数学的实践与认识2014，44（21）：228-236.

[16]徐文雄，张太雷，徐宗本.非线性高维自治微分系统SIEQR流行病模型全局稳定性[J].工程数学学报，2007，24（2）：79-86.

[17]刘茉， 宋燕， 许浩然，等. 具有连续接种且是非线性传染率的SIQR传染病模型[J].渤海大学学报（自然科学版）， 2010， 31（4）： 335-338.

[18]胡跃华， 肖革新， 郭莹， 等. 2008-2011年中国大陆手足口病流行特征分析[J].中国疾病控制杂志， 2014， 18（8）： 693-697.

[19]田辉， 杨培荣， 巨洲峰， 等. 气象因素对手足口病发病影响及预测模型分析[J]. 中国学校卫生， 2013， 34（4）：451-453.

[20]杨芳， 于石成， 张菊英， 等. 2008-2011年中国大陆地区重症手足口病流行特征分析[J].传染病监测， 2013， 28（11）：888-893.

[21]姚兴宽， 于杰. 2012年安阳市手足口病流行特征及病原学分析[J]. 应用预防医学， 2014， 20（4）：223-227.

（编辑：温泽宇）