挤压成型金属波纹管机械密封结构设计及应用

李万祥，马文忠，何 玮

（1.兰州交通大学机电学院，甘肃 兰州 730070；2.兰州交通大学艺术设计学院，甘肃 兰州 730070）

机械密封就是利用旋转轴进行自动密封，它是利用一对或是多对垂直轴在补偿结构弹力和流体压力下辅助密封完成轴封装置的密封，也被称为端面密封。随着机械密封环境的不断变化，对于传统的弹簧式机械密封结构，已经满足不了需求了，特备是一些腐蚀介质、高温场合想要不断适应现代发展需求，利用挤压成型金属波纹管机械密封建立相关装置，会带来更大的优势［1］。

1 金属波纹管挤压成型机械密封结构原理

机械密封东环的受力情况见图1。其中密封端液膜反力是Fc，密封介质作用力是F1、波纹管弹力是Fs、密封端面流体压力是Fm。所以得到东环合理是：

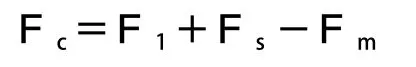
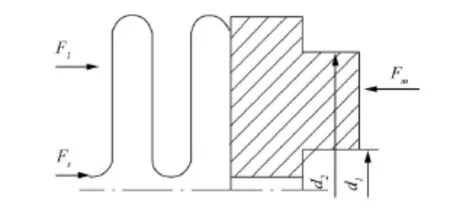
图1 波纹管密封机械东环受力

密封端面的介质不同压力也是不同的，其粘度也是不同的，得到液膜反压系数也是不同。

2 建立机械波纹管密封数学模型

关于选择金属波纹管挤压成型机械密封波纹管材料，需要具有耐腐蚀作用，以及也要有弹性，这里选择不锈钢0CR18Ni9材料，关于设计相关参数初始化见表1。

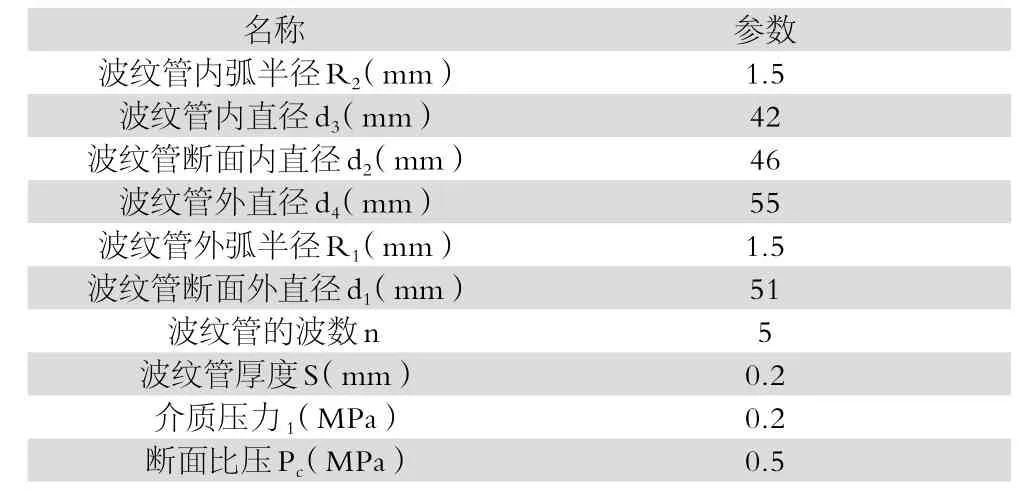
表1 机械波纹管密封设计初始参数

根据上述参数建立数学模型是：

（1）目 标 函 数（OBJ）：f（x）=f（x1,x2,……xn）；通过函数变量来判断方案设计的好坏，主要目的就是得到目标函数的极值。想要得到挤压成型波纹金属管机械密封管的尺寸，首先，要了解金属波纹管弹簧比压，根据密封断面和弹簧比压关系建立机械密封弹性力。如图1，初始化金属管的弹力是：

（2）变量状态（SV）。状态变量及时对因变量进行控制的值，它是变量的取值范围，以及状态变量限制空间条件，属于变量设计的函数。所以，设计机械密封时，最大的金属管应力强度（MaxN）需要符合使用材料的应力强度允许范围。

3 对机械密封结构模型进行求解

选择ANSYS优化设计方法将以增加问题的目标函数变成非约束形式的问题，建立目标函数、函数变量状态，来表达显函数。使用曲线拟合法，认为建立状态变量函数、目标函数的近似表达式，拟合状态变量和目标函数曲面公式：

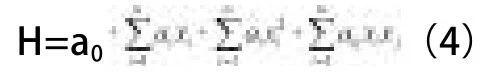
其中ai、bi、Cij属于方程的系数。在曲面拟合时，需要明确随机生成法建立的K组合变量，利用有限元方法得到相应的目标函数和状态变量值，这里K要比未知函数系数值大，即：得到每组结果总加权最小二乘误差是：

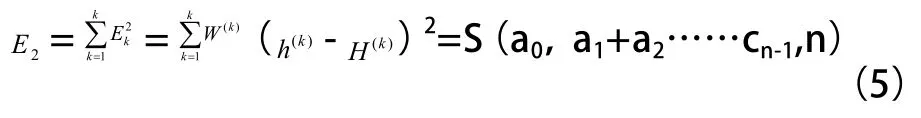
K是设计组数变量，H(k)是通过近似算法得到K组下的H值，h(k)是利用有限元法得到第K组的变量对应的H值，WK是K组变量的权，根据K组设计变量得到最小目标函数的设计空间和函数值。

4 机械密封模型最终优化设计结果

4.1 有限元模型的而建立

根据金属波纹管承载受力和结构特性，建立轴对称二维几何模型。利用4节点建立实体二维结构模型PLANE 42单元，将厚度分成3分，使用映射网格建立几何模型。通过计算得到6900个单元数目，节点术是9204。材料的参数是：泊松比µ＝0.3，弹性模量E＝195×103MPa，温度条件不考虑。加载有限元模型见图2。

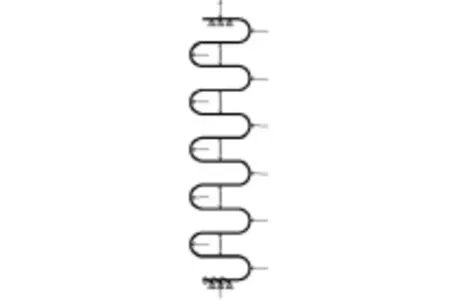
图2 有限元加载波纹管模型

4.2 结果优化

选择总长度是5%的初始位移波纹管压缩量，根据子步数200计算，将循环次数进行最大优化得到20，最终优化结果见表2。其中带有＊是最优化的结果。根据表中数据得到5次迭代程序收敛，得到最优化结果满足最大的应力强度是MAXN＝250.07MPa应力条件。

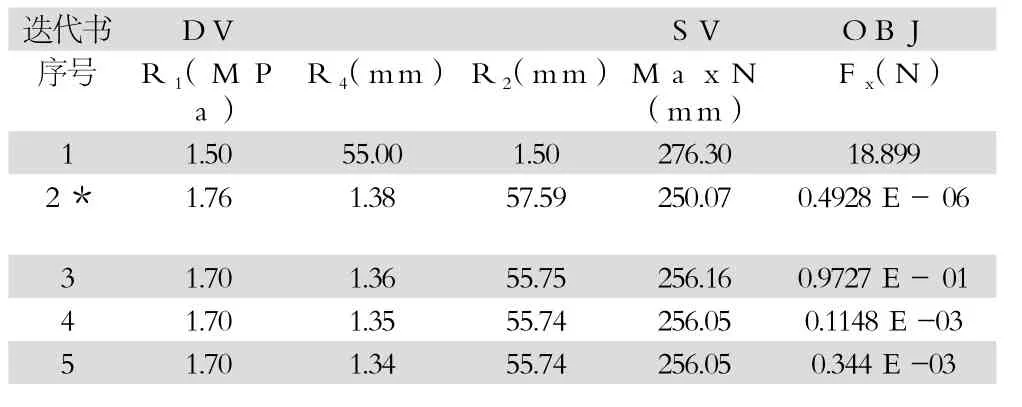
表2 迭代优化结果

5 结语

一般在选择挤压成型波纹管金属机械密封端面比压时，会先确定端面比压，在将金属波纹管弹力比压进行调整，这样可以保证密封端面压力不变，同时满足密封需求。根据上述数学模型的而建立，可以发现利用ANSYS有限元法对加压成型波纹管金属机械密封管进行优化，效果比较好，同时还能得到优化的金属波管结构，完成金属波纹管挤压成型机械密封设计。

[1]阿斯耶姆&#;肖开提,穆塔里夫&#;阿赫迈德,蒙伟安.焊接金属波纹管机械密封静环的温度场及热应力分析[C]//全国机械设计年会.2010.