基于菲涅尔衍射的圆孔直径测量

罗晓贺,惠 梅

(北京理工大学光电学院,北京 100081)

1 引 言

现有圆孔直径的高精度测量方法有很多,比较成熟的有采用工具显微镜和孔径干涉测量仪进行测量。其中工具显微镜可以达到微米级精度[1-3],孔径干涉测量仪可以达到亚微米级精度[3]。但是这些方法的测量仪器比较复杂,测量速度慢,同时对测量环境还有很高的要求,很难满足现代生产的需求。

为了实现在线测量,新的测量方法不断被提出,现主要有投影成像法和激光衍射法。

投影成像法是指在激光照射下将被测圆孔的阴影轮廓成像在光电探测器上,然后根据该阴影轮廓测量出圆孔直径。最典型的结构是准直系统加光电接收系统,该结构利用平行光投射被测物,并用已标定好放大率的光电接收系统对被测物阴影轮廓进行接收[4],最后利用图像处理的方法进行阴影轮廓的定位和尺寸测量[5],测得的阴影轮廓尺寸即为所求直径。该结构测量过程简单,但在测量过程中未考虑衍射效应造成的影响,使得阴影轮廓的定位误差较大。双光源投影法[6]针对上述结构进行了改进,该方法利用两个一定距离的点光源和无透镜的CMOS进行测量,设备简单；并在阴影轮廓定位时考虑了菲涅尔衍射的影响,将最大光强值的1/4处定位为轮廓。但是该定位方法受噪声影响比较大,进而精度受到限制。

随着衍射理论的发展,基于夫琅禾费衍射的尺寸测量方法被提出[7-9]。该方法利用圆孔的夫琅禾费衍射光强分布进行测量,精度较高。但是为了实现有限距离的夫琅禾费衍射,一般需要增加一个高精度的光学系统,在增加了测量成本的同时,还增加了仪器调整的复杂性。

本文将投影成像法和衍射理论进行结合,提出了一种新的测量方法——基于菲涅尔衍射的圆孔直径测量法。该方法由准直系统加无透镜CMOS组成。CMOS对平行光下的圆孔菲涅尔衍射光强分布图进行接收。通过探测光强分布图的峰值轮廓,再结合峰值轮廓尺寸和圆孔直径之间的关系式,达到直径测量的目的。该方法无需额外的光学系统,测量设备及测量过程简单,成本低,精度高,测量速度快,有望用于现代生产的在线测量。

2 测量原理

测量原理如图1所示。平行光束经过圆孔后发生菲涅尔衍射现象,衍射光强分布图被圆孔后距离d处的CMOS接收。CMOS被放置在电动平移台上,可以保证d在一定范围内高精度地变化。圆孔处的坐标系为o1x1y1,CMOS处的坐标系为oxy,oo1为光轴。圆孔所在的面和CMOS所在的面相互平行,且垂直于光轴。

在CMOS所接收的衍射光强分布图中,峰值轮廓和边界投影轮廓为同心圆,且半径差为m。2r为圆孔边界投影轮廓直径(等同于被测圆孔的直径),L是峰值轮廓直径,则2r=L+2m。L的具体数值可以通过对光强图进行图像处理获得,而m是关于λ、r和d的函数且未知。因而,本文的重点和难点是推导m关于λ、r和d的关系表达式(又称峰值定位公式)。

图1 测量原理图及衍射光强图。图示光强分布对应参数:

2.1 圆孔菲涅尔衍射光强分布

根据基尔霍夫衍射公式[10],平面波照射下,圆孔菲涅尔衍射的复振幅公式为:

(1)

根据光强和复振幅之间的关系,可得光强为:

I(x,y)=|E(x,y)|2

(2)

圆孔是一个中心对称的图形。故而只需求得其中一条直径线上各点的光强值即可。假设圆孔直径2r=5 mm,衍射距离d=300 mm,观察线为:y=0,x∈[-2.5,2.5] mm。根据公式(1)和(2),求得的观察线上各点的光强分布如图2中黑色实线所示。

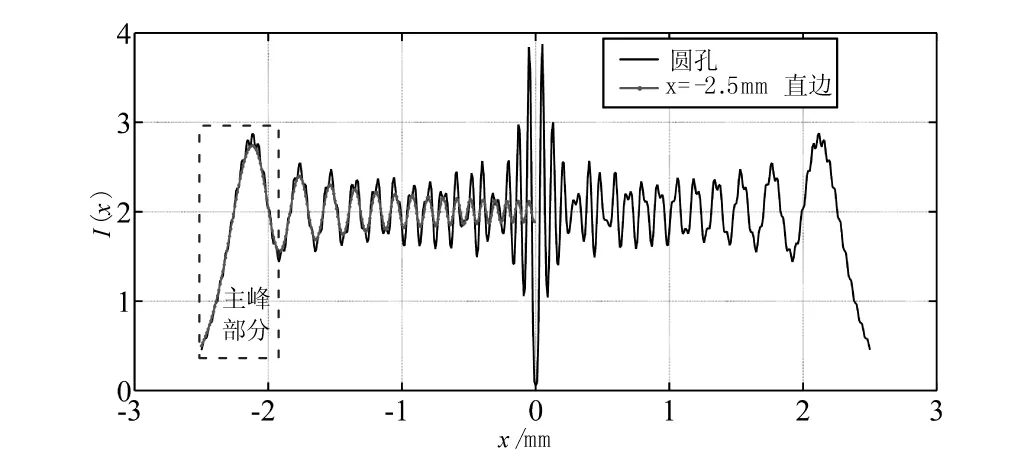
图2 圆孔及直边菲涅尔衍射光强分布曲线

2.2 峰值定位公式

根据文献[11],平行光照射下,直边菲涅尔衍射对应的峰值点和边界投影点之间的距离mz满足条件:(2/λd)0.5mz=1.2172,即mz=0.8607(λd)0.5。

在图2中,点实线表示位于x1=-2.5 mm处的直边菲涅尔衍射光强分布曲线,该曲线对应的观察线为:y=0,x∈[-2.5,0]。很显然,图2中两条光强分布曲线的主峰部分(即包含最大峰值在内的峰区域)非常相似,黑色实线相当于在点实线的基础上添加了一些小波动。如果忽略小波动的影响,圆孔菲涅尔衍射光强分布中峰值位置与边界投影的距离m等同于mz,即满足公式:

(3)

但是小波动的存在使得公式(3)有一定的误差Δm,为分析该误差数值,仿真如下:

假设圆孔直径2r=5 mm,衍射距离d∈[10,500] mm,观察范围为:y=0,x∈[-2.5,2.5] mm,光强图的像元尺寸为5.5 μm。通过对光强分布的主峰部分数据进行多项式拟合的方法获得峰值的精确位置,进而得到仿真的m值(称为“拟合值”)。不同衍射距离d对应的m的拟合值如图3(a)所示；根据公式(3)计算所得的m也同时绘制于图3(a)中,称为“理论值”。观察图3(a)可知,m的拟合值和理论值非常相近,两者的差值即为公式(3)的误差值Δm,峰值定位误差曲线d-Δm被绘制于图3(b)中。

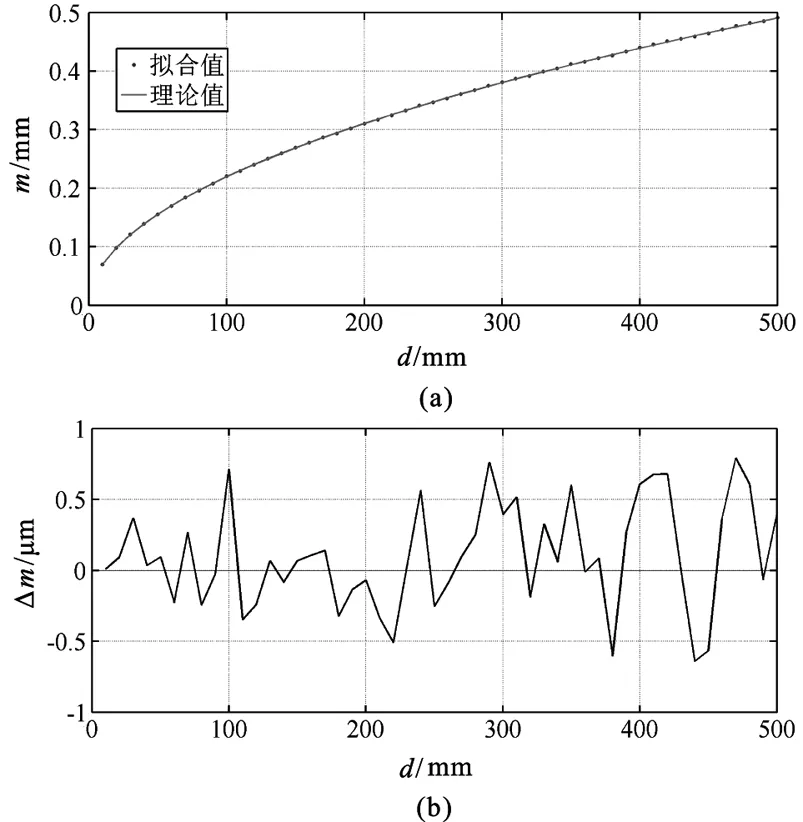
图3 峰值定位公式曲线及峰值定位误差曲线

图3(b)中的峰值定位误差曲线是针对2r=5 mm的情况。现改变2r的数值为7.5 mm、10 mm、12.5 mm和15 mm,可以得到其余四条峰值定位误差曲线。现对该5条误差曲线进行分析,提取出曲线的分段最大值,并列于表1中。

表1 峰值定位误差分段最大值

注：max(|Δm|)表示在一定衍射距离范围内|Δm|的最大值。

根据表1中的数据可得:(1)当衍射口径尺寸2r不变时,峰值定位误差的数值会随着衍射距离d的增加而增加；(2)当衍射距离d固定时,峰值定位误差的数值会随着衍射口径尺寸2r的增加而减小。

因此,针对每一个被测孔,为减小测量误差,实际测量中所用的衍射距离d应尽量小。

2.3 圆孔直径计算公式

根据公式(3),可以推出峰值轮廓的直径为:

(4)

在实际测量中,衍射距离d的绝对值很难精确得知,但是d的相对变化量可以非常精确(利用电动平移台可达到0.1 μm的精度)。故而我们采用两个不同衍射距离的衍射图来进行测量。具体的操作过程为:采集两个相对位置Δd已知的两衍射光强图,根据这两图得到对应的峰值轮廓直径L1和L2,结合公式(4)可得被测圆孔的直径为:

(5)

3 实 验

为了验证分析结果,在实验室中进行了一系列的实验。

3.1 实验装置

搭建实验装置如图4所示。

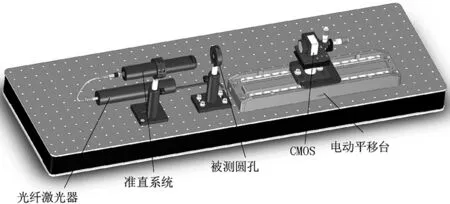
图4 实验装置示意图

在图4中,光源采用波长为647 nm的光纤激光器；准直系统选用口径为25 mm,焦距为200 mm的双胶合透镜；被测圆孔为三个标准圆孔,标称尺寸分别为5 mm、7.5 mm和10 mm；CMOS的像元尺寸为5.5 μm×5.5 μm,分辨率为2048×2048；CMOS被安装在一个电动平移台上,该平移台的移动灵敏度为0.1 μm。在采集图像之前,CMOS的靶面调整至与光轴方向垂直,平移台移动方向调整至与光轴方向平行。

3.2 图像采集及数据处理

3.2.1 10 mm圆孔的测量

先测量标称尺寸为10 mm的圆孔。

受限于机械结构,CMOS和被测圆孔之间的最小距离大于95 mm,故而我们移动平移台,使得初始衍射距离约为100 mm并采集图像,该位置记为初始位置。为了提高信噪比,我们控制CMOS在每个位置自动快速连续采集30幅图,然后计算出它们的均值图用于后续的计算。

以初始位置为基准,以1 mm的间隔向后连续移动电动平移台99次,总共获得100幅均值衍射图像,分别标记为I1～I100。现将I1～I100分为两组,I1～I50为第一组,I51～I100为第二组。根据公式(5),两组图两两结合计算圆孔直径,即I1和I51结合,I2和I52结合,依次类推。此时两图之间的位置间隔Δd=50 mm。图像处理的界面如图5所示,图中显示的为I1和I51的图像处理过程。

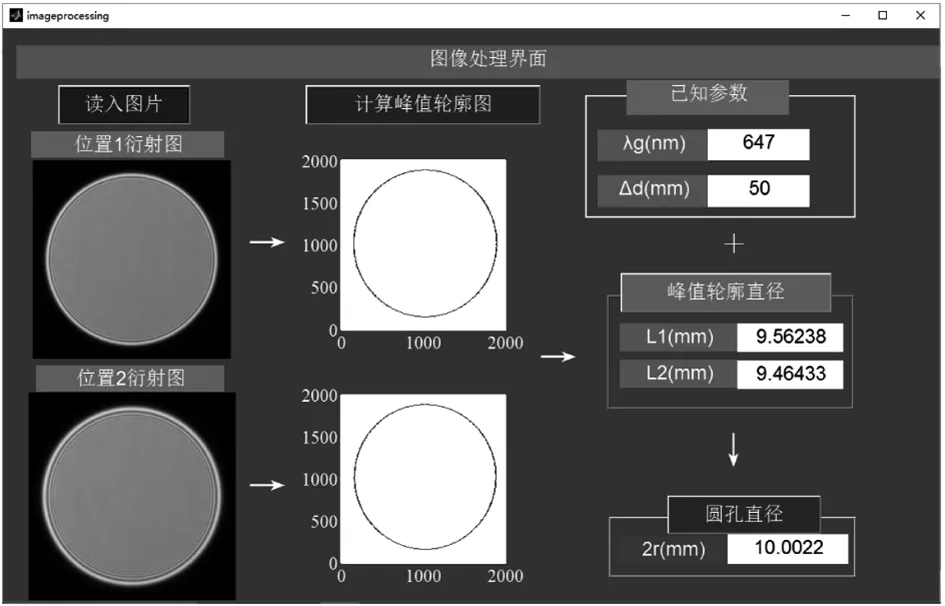
图5 图像处理界面

重复图5所示的过程,可以得到50个圆孔直径的测量值2r,并绘制于图6中。

图6 10 mm圆孔测量结果曲线

图6中的横坐标表示这50对衍射图像的序号,纵坐标为相应的圆孔直径测量值。我们以图I1～I50对应的衍射距离d表示这50对衍射图的位置。很显然,随着序号的增加,衍射距离逐渐增加,而对应的圆孔直径测量值没有明显的变化,因此这50个测量值的波动范围可以看作是该方法的测量精度。

根据图6曲线可知:50组测量值相对于均值的最大偏差为0.3737 μm。因此,利用菲涅尔衍射测量10 mm圆孔直径的测量精度为0.3737 μm。

3.2.2 7.5 mm和5 mm圆孔的测量

重复3.2.1的过程,测量标称尺寸为7.5 mm和5 mm的圆孔直径,所得的测量结果曲线分别如图7和8所示。

图7 7.5 mm圆孔测量结果曲线

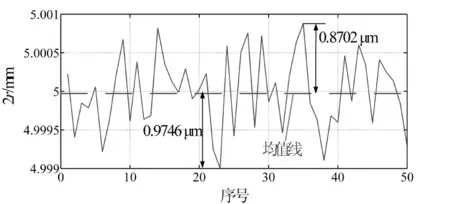
图8 5 mm圆孔测量结果曲线

根据图7和图8的曲线可知:利用菲涅尔衍射法测量7.5 mm和5 mm圆孔直径的测量精度分别为0.6726 μm和0.9746 μm。

综上,该方法对于5～10 mm范围内的圆孔可以达到亚微米级的精度；在相同的测量条件下,圆孔直径越大,测量精度越高,这和2.2的结论相同。

4 结 论

本文提出了一种基于菲涅尔衍射的圆孔直径测量的方法。该方法将直径测量转换为峰值位置的检测。该方法的测量仪器非常简单,仅仅需要一个平移台和一个CMOS即可；而且计算很快,只需要寻求峰值位置即可,所以可以用于在线测量。仿真和实验数据显示,该方法对于5～10 mm范围内的圆孔可以达到亚微米级的精度。

[1] JIN Ming.The uncertainty evaluation for measurement result of circle hole diameter with multi-tool microscope double-chord measured method[J].Metrology & Measurement,2007,34(11):11.(inChinese)

靳明.工具显微镜双弦法测量圆孔直径的测量结果的不确定评定[J].计量与测试技术,2007,34(11):11.

[2] JIE Sanxia,FAN Weijun.Research on application of image method detection based on visualuniversal tool-microscope[J].Laser & Infrared,2010,40(9):997-1000.(in Chinese)

解三霞,范伟军.目视万能工具显微镜的影像测量应用研究[J].激光与红外,2010,40(9):997-1000.

[3] LI Yan.Technology of precision measurement [M].Beijing:Standards Press of China,2008.(in Chinese)

李岩.精密测量技术[M].北京:中国标准出版社,2008.

[4] ZHANG Jianrong,JIANG Yuming.Research into a method for on-line CCD imaging measurement of the diameter of glass rod [J].J.Applied Optics,2004,25(3):53-56.(in Chinese)

张建荣,姜昱明.CCD成像在线测量玻璃棒直径的方法研究[J].应用光学,2004,25(3):53-56.

[5] ZHANG Tieying,BAI Fuzhong,SONG Xiaoyan,et al.Image measuring method for width of straight-edge object[J].Laser & Infrared,2014,44(2):222-226.(in Chinese)

张铁英,百福忠,宋小燕,等.一种直边缘物体宽度的图像测量法[J].激光与红外,2014,44(2):222-226.

[6] ZHAO Bin,YAN Weibin.Measurement of wire diameter by two point sources projection [J].Optics and Precision Engineering,2003,11(2):171-175.(in Chinese)

赵斌,颜伟彬.双光源投影法细丝直径测量[J].光学 精密工程,2003,11(2):171-175.

[7] ZHAO Yuliang,XU Zhaolin.Amelioration and precision improving of slit width measurement system based on the orthogonal linear CCD [J].Infrared and Laser Engineering,2006,35(1):75-77.(in Chinese)

赵育良,许兆林.基于CCD的微缝宽激光测量系统的改进[J].红外与激光工程,2006,35(1):75-77.

[8] YANG Ping,ZHANG Yujie.Research on laser diffraction in pass measurement of wire drawing dies[J].Laser & Infrared,2017,47(2):150-153.(in Chinese)

杨萍,张玉杰.激光衍射在拉丝模孔型测量中的研究[J].激光与红外,2017,47(2):150-153.

[9] YANG Sa.Using CCD censor to receive the Laser diffraction andmeasure the precise slot width and round hole radius [J].Journal of the Hebei Academy of Sciences,2009,26(3):13-15.(in Chinese)

杨飒.利用CCD 接收激光衍射的方法测量精密缝宽和圆孔直径[J].河北省科学院学报,2009,26(3):13-15.

[10] XIE Jinghui,ZHAO Dazun,YAN Jixiang.Physical optics course [M].Beijing:Beijing Institute of Technology Press,2012.(in Chinese)

谢敬辉,赵达尊,阎吉祥.物理光学教程[M].北京:北京理工大学出版社,2012.

[11] LUO Xiaohe,HUI Mei,ZHU Qiudong,et al.Quantum-mathematical model of edge and peak point in Fresnel diffraction through a slit [J].Chin.Phys.B,2017,26(5):054202.