碲锌镉晶体生长全局热传递模拟模型准确度研究

刘江高,吴 卿

(华北光电技术研究所,北京 100015)

1 引 言

碲锌镉单晶材料是制备高性能长波、甚长波碲镉汞红外焦平面探测器的最佳衬底材料。但是碲锌镉晶体作为化合物半导体材料,晶体的层错能以及临界剪切应力较低,使得高质量碲锌镉晶体的制备变得非常困难,成为限制其应用的关键所在。目前,垂直布里奇曼法(VB)和垂直温度梯度法(VGF)是生长碲锌镉晶体主流途径。而采用VB法或者VGF法生长碲锌镉晶体材料时,晶体的生长过程往往无法直观观察,晶体内部的温场也缺乏相应的手段检测,这对改进晶体生长工艺带来了诸多不便。随着数值模拟技术的发展,利用计算机仿真能够将晶体生长的过程重构或再现,很好地解决了这方面问题。同时,数值模拟软件可在任意改变热场结构和工艺参数的情况下研究不同晶体的生长过程,使其成为研究晶体生长、开发晶体生长工艺设备的越来越重要的工具。已经有相当多的报道[1-4]利用数字模拟的方法研究了晶体生长过程中各参数对晶体生长结果的影响规律。但是,在实际碲锌镉长晶设备以及长晶工艺开发过程中,从模拟计算得到的这些影响规律中寻找到适合晶体生长的外在条件还需要较大的实验量,晶体生长研发难度依然很大,研发周期也比较漫长。有鉴于此,如果能够建立与实际炉体对应的全局热传递模型,综合考虑整个体系的热传导、辐射以及对流等问题,最大化地减小模型和实际温场的差异,通过晶体生长模拟获得的最优结果能够直接应用于实际长晶过程,那么相应工艺的研发周期就能大大缩减,晶体生长工艺质量也能够获得明显提升。在B.Brikmann等人的研究[5]中,他们将模拟计算结果温度与实际温度差距缩小到19K,然后利用模拟的结果进行GaAs晶体实验生长,获得了非常好的结果。但是,对于采用VB法以及VGF法生长的碲锌镉晶体而言,其生长的温场温度梯度已经降到10K/cm以下,模拟计算的温度误差必须足够小才能将模拟计算的结果直接应用于碲锌镉晶体长晶设备以及工艺的开发。因此,提高碲锌镉晶体模拟技术的准确性显得尤为重要。本文即采用俄罗斯STR公司的CGSim晶体生长模拟软件,通过研究几何模型、材料物性参数、温度设定条件等对碲锌镉晶体单晶炉全局热传递模型准确性的影响,并比较计算结果和实际结果的差异,修正模型,最终获得了具有较高准确度的全局热传递模型。

2 模拟计算模型

图1是VB法生长碲锌镉单晶的单晶生长炉的理论计算模型,其整体高度为1.4 m,与实际炉体高度差距在3 cm以内。该炉体总共由六温区构成,每个温区由相应的控温热偶进行控温,为保证准确度,网格在界面处都进行了细化。研究过程中,为了能够评价模拟模型的准确度,本研究使用了S型热偶测量炉膛内部温度,将S型热偶插入炉膛中央,通过慢拉热偶并保温的形式测量炉膛各位置点温度,形成位置—温度曲线,作为模拟计算结果的参考标准。模拟计算过程,利用CGSim软件PID计算的功能[6-8],模拟实际设备控温热偶进行控温,通过给定特定位置点处温度,反向计算各温区需要的加热器的功率,然后获得炉体内部的温场曲线,并比较模拟获得的温场曲线与实际测温的曲线差异。模型中所用炉管的材质为康泰尔合金和高纯氧化铝陶瓷,炉壳为不锈钢结构,保温材料是由莫来石纤维压制。常见材质的物性参数如表1所示。

图1 模拟计算采用的炉体模型图

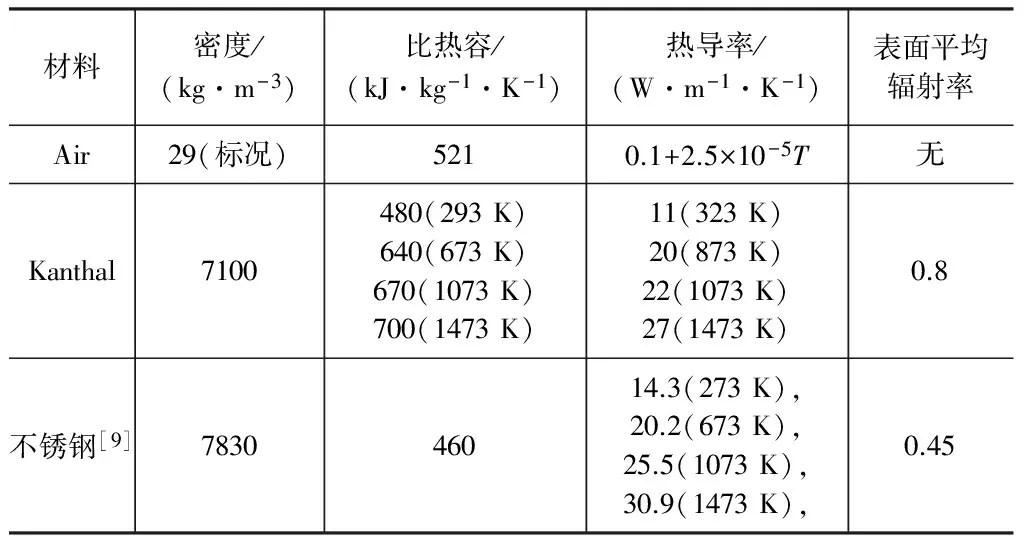
材料密度/(kg·m-3)比热容/(kJ·kg-1·K-1)热导率/(W·m-1·K-1)表面平均辐射率Air29(标况)5210．1+2．5×10-5T无Kanthal7100480(293K)640(673K)670(1073K)700(1473K)11(323K)20(873K)22(1073K)27(1473K)0．8不锈钢[9]783046014．3(273K)，20．2(673K)，25．5(1073K)，30．9(1473K)，0．45

注：T为开尔文温度。

3 各参数对全局热传递模型精度影响

3.1 几何模型对计算结果精度的影响

晶体生长过程涉及到固液界面在炉体中的位置。应用模拟的温场,必然需要准确的晶体生长位置,特别对于在炉体温场梯度区域。以一个温度梯度为5 K/cm的温场为例,当模拟结果与实际位置相差1 cm时温度就会差别5 ℃,这种误差对于我们管理籽晶处的温度将非常致命,可能使籽晶完全熔化。因此几何模型各温区与测温结果的对应显得尤为关键。图2给出了应用测温曲线位置偏差时的模拟温场的对比,温场中不仅相同位置温度差别巨大,同时模拟温场的形状也无法与实际温场对应。

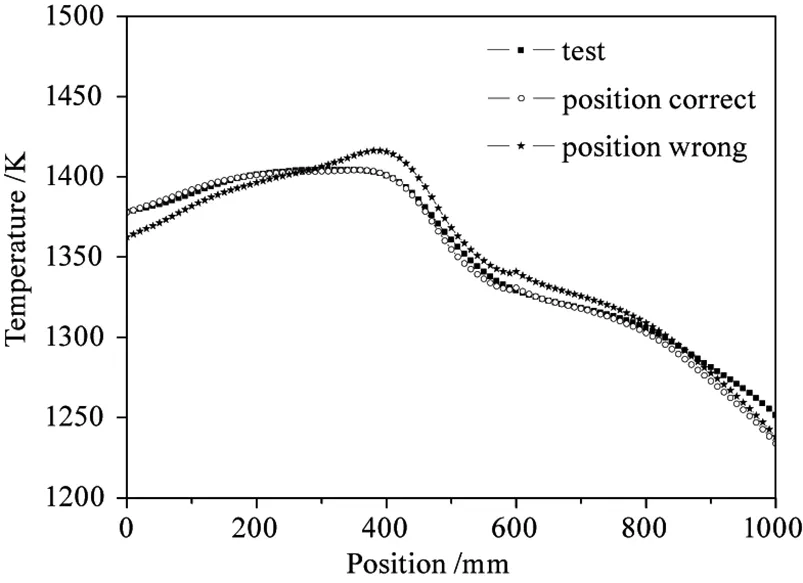
图2 几何位置不同时的模拟温场结果与真实测量值结果比较

另外在实际应用过程中,许多特殊的实际结构,由于模拟软件的限制,很多时候并不能建立与实际几何形状一样的模型。这种情况下需要我们进行相应的模拟修正。典型的如单晶炉中比较常见的炉丝结构是螺旋结构,这在平面2D模拟软件中无法实现。因此,2D模型中采用的炉丝一般结构如图3所示有两种。

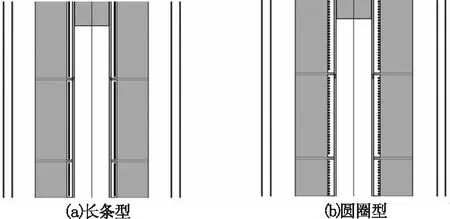
图3 两种炉丝结构模型

2D模型中的长条型结构实际对应于3维空间的圆筒式加热结构,而圆圈型结构对应于多炉丝环结构。在给出了以相同的控温设定情况下,二者对应炉体内部温场如图4所示,可以看到二者整个部分差别并不大。另外,根据各自功率计算情况,长条炉丝总加热功率为2580 W和圆圈炉丝的总加热功率为2610 W,在功率上也未有较大的差别。所以,对本案例来说,两种模型都可以用于全局模型的模拟计算。

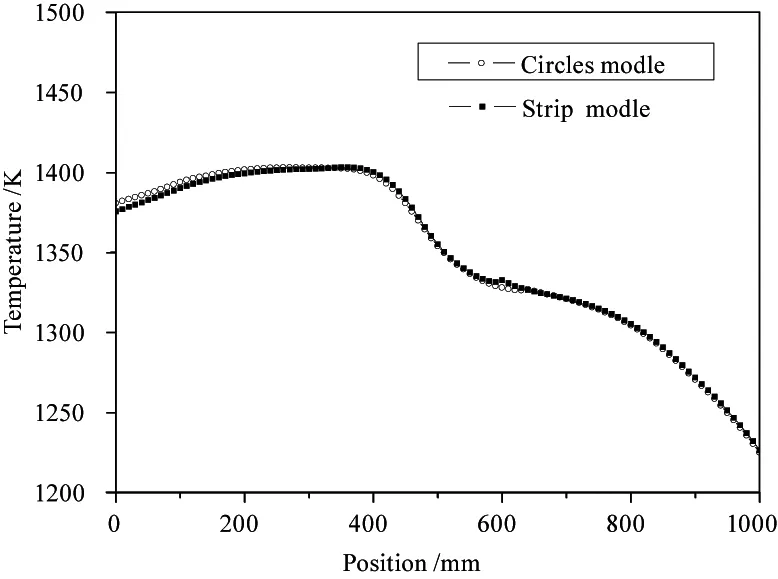
图4 两种炉丝结构下温场模拟结果对比

3.2 材料物性参数对计算结果的影响

相对准确的材料参数是建立准确全局热传递模型的前提。对于常见的碲锌镉晶体生长过程涉及到的材料,如石英,石墨,不锈钢等材料,它们的成分较为简单,物性参数可以通过各种工具书都能够查到比较准确可信的值。但对于有些材料的物性参数,无法在各文献中获得统一的值,需要模拟手段进行验证。如高纯氧化铝材质的炉管在常温时的热导率在文献[9]中就有两种不同的值。利用文献中氧化铝的热导率分别计算炉体内部温场结果如图5所示,差别主要在圆圈标记中有体现,差异的位置位于炉膛底部,对比发现高纯氧化铝的导热率为3 W/(K·m)时的温场结果与测温结果更加吻合,因此通过模拟计算与实际比较就可以确认高纯氧化铝常温时3 W/(K·m)将更适合用于建立准确的全局热传递模型。

图5 炉管材料在常温热导率不同时模拟结果与实际测温结果的对比

另外,对于一些未有标准制备工艺的材料,如炉体中的耐火保温材料,它们的物性参数直接受制备工艺和最终成型的特点影响,无法通过查阅文献获得参考值。而高温下其物性参数也与室温有较大的不同,这些参数在高温时测量起来也较为困难,要想获得准确值,也需要在模拟模型中计算验证。表2给出了在相同的模型以及设定温度条件下,通过CGSim软件计算获得了保温材料热导率不同时加热器的功率。可以看到随着保温材料的导热率上升,将加热器的功率将逐渐升高,而保温材料的热导率在0.24 W/(K·m)时模拟结果更为准确。

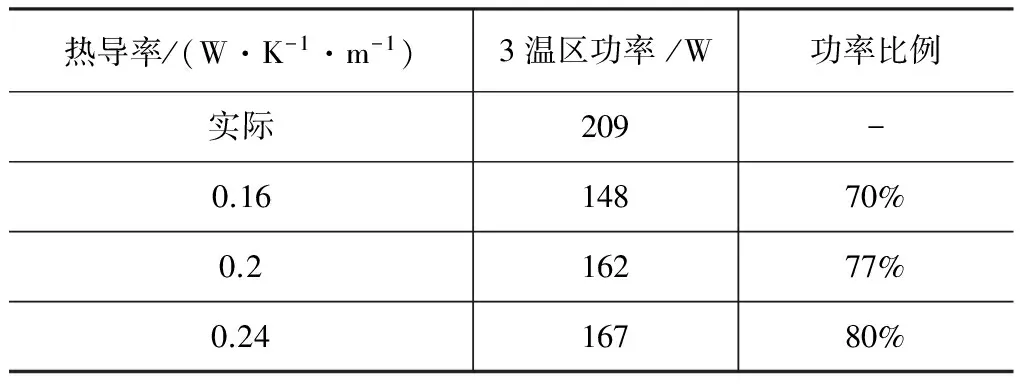
表2 耐火保温材料不同热导率情况下温区功率对比

3.3 温度设定边界条件对计算结果的影响

理论计算的模型,边界条件的准确与否也直接关系到计算结果的准确度。对于反向计算加热器功率的计算方式,非常重要的边界条件就是寻找加热器功率所需要的控温热偶的位置和温度。计算过程中,控温热偶的位置和温度直接影响炉丝加热功率的大小,继而决定炉膛内部温场。实际上,由于侧面控温热偶对测量点处温场影响较大,其测量温度相较于炉体内部单独的测温热偶有较大的偏差,图6即给出了采用控温热偶测量温度为边界条件设定得到的模拟结果。可以看出二者曲线温度存在较大的差异,部分位置温度差异在20 ℃以上。

因此要想得到准确的模拟模型,需要对控温热偶的边界条件进行修正。修正方式有两方面,一方面是选用实际控温热偶插入的位置,比较模拟结果的温度与控温热偶的温度,其差值作为体系模拟值与实际值的固定参考差值；另一方面是以实际控温热偶测量温度为准,选择合适的控温点位置,这种以测量温度为参考点,意味着模拟结果上所有等温线上的点都满足要求,所以一般以离炉丝较近处且区域的温度梯度不大的点作为控温点。而由于实际问题的复杂性,模型控温可能会与实际控温有较大的差异,这种修正后的结果还需要进行多次调温测温实验来验证,才能最终筛选出最优化的控温热偶的控温参考以及控温位置。具体而言,就是实际测温时改变温度设定然后在模拟模型中改变模型对应的温度设定相同的幅度进行模拟,并比较新温场设定下模拟结果与实际测温的差别。通过模拟结果与测温结果对比,如果模拟结果与实际结果还能吻合良好,说明模拟模型控温点的位置以及控温温度的设定准确度较高,能够在后续晶体模拟生长中使用。图7即在优化过的控温位置及控温温度的基础上,改变各控温点温度设定,比较模型模拟计算结果与实际测温结果。可以看到两种设定条件下,模型模拟结果都能与实际温场曲线吻合,证明了选择的控温点位置和参考温度的正确性。

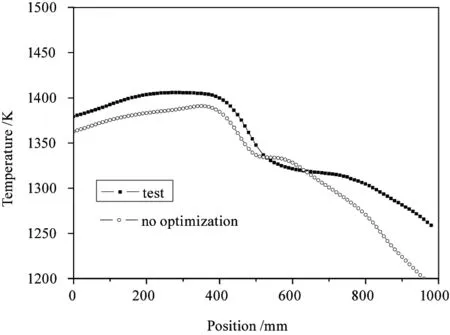
图6 温度设定边界条件未优化时模拟结果与实际对比

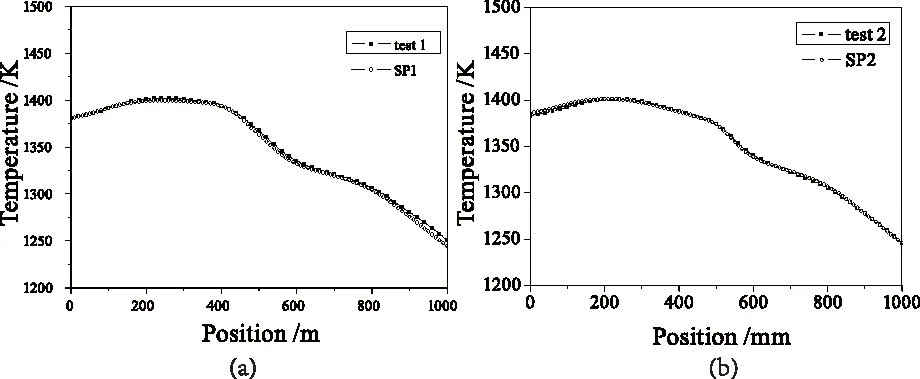
图7 两种设定温度条件下,模拟结果

在获得了以上各部分的最终优化后的全局热传递模型之后,本研究也利用该模型计算了碲锌镉晶体生长过程。图8给出了生长过程中晶体头部监测点实际监测温度与模拟模型中的对应监测点温度的比较。可以看到整个长晶过程,监测温度与模拟获得温度差异已经能控制到2 ℃以内,更加有利于我们研究碲锌镉晶体的生长过程。

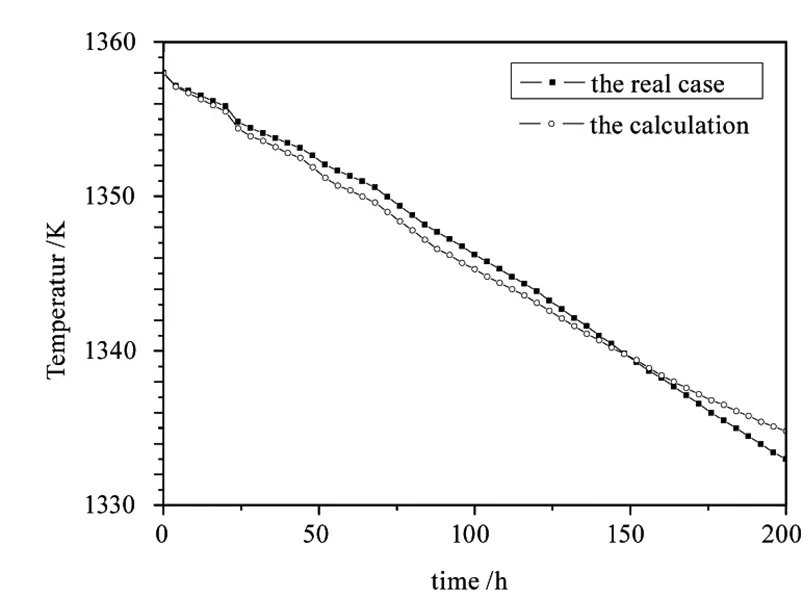
图8 实际晶体生长过程监测点的模拟结果与实际测量结果对比

4 结 论

全局热传递模型由于涉及到传热的三种基本机制,复杂程度较高,其准确度需要一定的方式进行校准提高。模型的几何参数、物性参数以及控温设定参数都会显著地影响全局热传递模型的准确度。在实际修正模拟模型过程中,可以以炉体中心准确测量的温度值以及各加热器的实际功率为参考,比较模型计算结果与实际结果的符合程度,修正模型各参数,然后并在不同的控温设定条件下验证模型的准确度,得出最优化的模型。在此基础上再进行晶体生长过程模拟,将更容易得到能够直接指导实际炉体调试的工艺参数。

[1] ZHANG Guodong,LIU Juncheng.Effect of temperature gradient on thermalstress filed of CdZnTebridgman crystal growth [J].Journal of Functional Materials and Devices,2009,(02):106-112.(in Chinese)

张国栋,刘俊成.温度梯度对碲锌镉单晶体生长过程热应力场的影响 [J].功能材料与器件学报,2009,(02):106-112.

[2] Nan Zhang,Anderew Yeckel,Jeffrey J Derby.Maintaining covex interface shapes during electrodynamic gradient freeze growth of cadmium zinc telluride using a dynamic bell-curve furnace profile [J].Journal of Crystal Growth,2012,355:113-121.

[3] WANG Siai,SU Xiaoping,ZHANG Fen,et al.Numerical simulation study on impact of cone angle of crucible on VGF GaAs monocrystal growth [J].Chinese Journal of Rare Matals,2011,35(4):525-530.(in Chinese)

王思爱,苏小平,张峰,等.数字模拟法研究坩埚锥角对VGF法GaAs单晶生长的影响 [J].稀有金属,2011,35(4):525-530.

[4] TU Fan,SU Xiaoping,ZHANG Fen,et al.Optimization of gap between crucible and support during growth of 6 Inch VGF GaAs single crystal by numerical simulation [J].Chinese Journal of Rare Matals,2011,35 (4):617-622.(in Chinese)

涂凡,苏小平,张峰,等.6英寸砷化镓单晶VGF法生长中坩埚-埚托间隙对晶体生长过程的影响 [J].稀有金属,2011,35 (4):617-622.

[5] B Brikmann,M Rasp,J Stenzenberger,et al.Growth of 3″ and 4″ gallium arsenide crystals by the vertical gradient freeze (VGF) method [J].Journal of Crystal Growth,2000,211:157-162.

[6] Yu E Egorov,Yu N Makarov,E A Smirnov,et al.Nelson (Eds.),Semiconductor Process and Device Performance Modeling [C].Mat.Res.Soc.Symp.Proc.,vol.490,MRS,Pennsylvania,1998:181.

[7] V V Kalaev,L Yu Evstratov,Yu N Makarov.Gas flow effect on global heat transport and melt convection in Czochralski silicon growth [J].Journal of Crystal Growth,2003,249:87-89.

[8] O V Smirnova,V V Kalaev.3D unsteady numerical analysis of conjugate heat transport and turbulent laminar flows in LEC growth of GaAs crystals [J].International J.of Heat and Mass Transfer,2004,47:252-371.

[9] YANG Jungang.Foundation of material heating furnace[M].Xi′an:Northwestern Polytechnical University press,2009:115-116.(in Chinese)

杨君刚.材料加热炉基础[M].西安:西北工业大学出版社,2009:115-116.