基于全采样和L1范数降采样的卷积神经网络图像分类方法

宋婷婷，徐世许

（青岛大学自动化与电气工程学院，山东 青岛 266071）

0 引言

近年来，随着计算能力的提升和卷积神经网络的发展，卷积神经网络在图像分类任务中的表现逐年变强，相比全连接神经网络[1-4]的性能提升了很多。自2012年，AlexNet[5]获得ILSVRC（ImageNet Large Scale Visual Recognition Challenge）图像分类项目冠军之后，2014年亚军、2014年冠军和 2015年冠军也分别被卷积神经网络 VGGNet[6]、Google InceptionNet[7]和ResNet[8]获得。在卷积神经网络中，池化层对分类性能有重要影响。根据 Springenberg等[9]的分析，池化层的作用相当于卷积层中的激活函数，只是用p范数替代了激活函数。池化层通过减小输入尺寸来减少后一层的参数量和计算量。在最大池化层中，每个池化窗口中最大值被认为是对分类“最有用”的信息而得以保留，其余信息被丢弃。而实际上，被丢弃的信息也可能对分类任务来说是有用的。针对最大池化的这一问题，本文提出全采样方法和基于 L1范数的降采样方法替代最大池化层，在CIFAR-10和MNIST数据集上的实验结果表明，在网络结构相同、参数不增加的情况下，所提方法的分类准确率高于最大池化方法。

1 全采样和基于L1范数的降采样

1.1 全采样

全采样包括重新组织输入信息和使用 1×1卷积恢复通道数两步。以尺寸为4×4、通道数为L的输入为例，介绍全采样是如何重新组织输入的。如图1所示，输入包括16个尺寸为1×1、通道数为L的张量（多维数组），并且进行了编号。一个尺寸为2×2，步长为2的窗口遍历输入，窗口中的四个张量被抽取出来，然后滑动窗口，重复上述操作，直至遍历结束。把每次抽取出来的相同位置上的张量拼成尺寸为2×2，通道数为L的张量，然后把这四个张量在通道维度上拼接成尺寸为2×2，通道数为4L的张量。为了把通道数恢复为L，后紧跟一个包含L个1×1卷积核的卷积层。

1.2 基于L1范数的降采样

如果要减少全采样过程中 1×1卷积层的参数量，可以保留每个窗口的4个张量中L1范数最大的k∈ { 1,2,3}个张量，而不是所有的张量，这就是基于L1范数的降采样方法。假设原输入尺寸为 DF×DF（要求 DF为大于零的偶数），通道数为 L。图 2给出了使用 L1范数进行降采样(k=3)的示意图，DF= 4 。使用tensorflow[10,11]实现的具体步骤为：

步骤一，对原输入进行切片，得到四个新输入，第一个新输入与原输入相同，第二个新输入是原输入右边 DF×(DF-1)的部分，第三个新输入是原输入下边(DF- 1 )× DF的部分，第四个新输入是原输入右下(DF- 1 )× ( DF- 1 )的部分；

步骤二，对每个新输入进行1×1、步长为2的最大池化，得到四个张量，每个张量的尺寸为

步骤三，计算步骤二得到的四个张量的 L1范数；

2 卷积神经网络结构

为了比较全采样方法、基于L1范数的降采样方法和最大池化方法，本文使用结构相同的四个神经网络：FS-CNN、L1-Norm-CNN(k=3)、L1-Norm-CNN(k=2)和MP-CNN。每个神经网络的结构和参数如表1所示。受VGGNet启发，堆叠3×3卷积层就可以获得不错的分类准确率，每个卷积神经网络都只使用 3×3的卷积层。每个卷积层后都紧跟一个BN（Batch Normalization 批归一化）层[12]用于加速训练过程，再使用ReLU（Rectified Linear Unit修正线性单元）层[13]作为激活函数。

（1）FS-CNN（Fully-Sampled-CNN）。第一层和第二层都是卷积层，分别包含96个3×3卷积核。第三层是全采样层，包含一个96个1×1卷积核的卷积层。第四层和第五层是卷积层，分别包含 192个3×3卷积核。第六层是全采样层，包含一个192个1×1卷积核的卷积层。第七层是包含192个3×3卷积核的卷积层。第八层是包含192个1×1卷积核的卷积层。第九层是包含10个1×1卷积核的卷积层。第十层是全局平均池化层，滑动窗口尺寸为7×7，得到尺寸为 1×1、通道数为 10的输出，正好对应下小节实验中CIFAR10和MNIST的图片种类。最后一层为softmax层。

（2）L1-CNN(k=3) (L1-Norm-CNN with k=3)。与FS-CNN的区别在于，L1- CNN(k=3)的第三层和第六层换成了基于 L1范数的降采样层，选取了 3个L1范数最大的张量。

（3）L1-CNN(k=2)。与 L1-CNN(k=3)的区别在于，L1-CNN(k=2)降采样层选取了2个L1范数最大的张量。

（4）MP-CNN（MaxPool-CNN）。为了说明FS-CNN比MP-CNN的性能提升既不是因为结构不同导致，也不是因为增加参数导致，把MP-CNN的最大池化层的输出拷贝4份，然后在通道维度上拼接起来，后接一层 1×1卷积层，使 MP-CNN和FS-CNN的结构和参数个数都相同。

3 实验结果

实验开发平台为Tensorflow 1.2 GPU版本，使用 Python 3.4作为开发语言，使用 cuda8.0和cudnn5.1作为运算平台，开发系统为ubuntu14.04。硬件平台主要元件的规格型号如表2所示。

图1 全采样过程示意图Fig.1 Full sampling process diagram

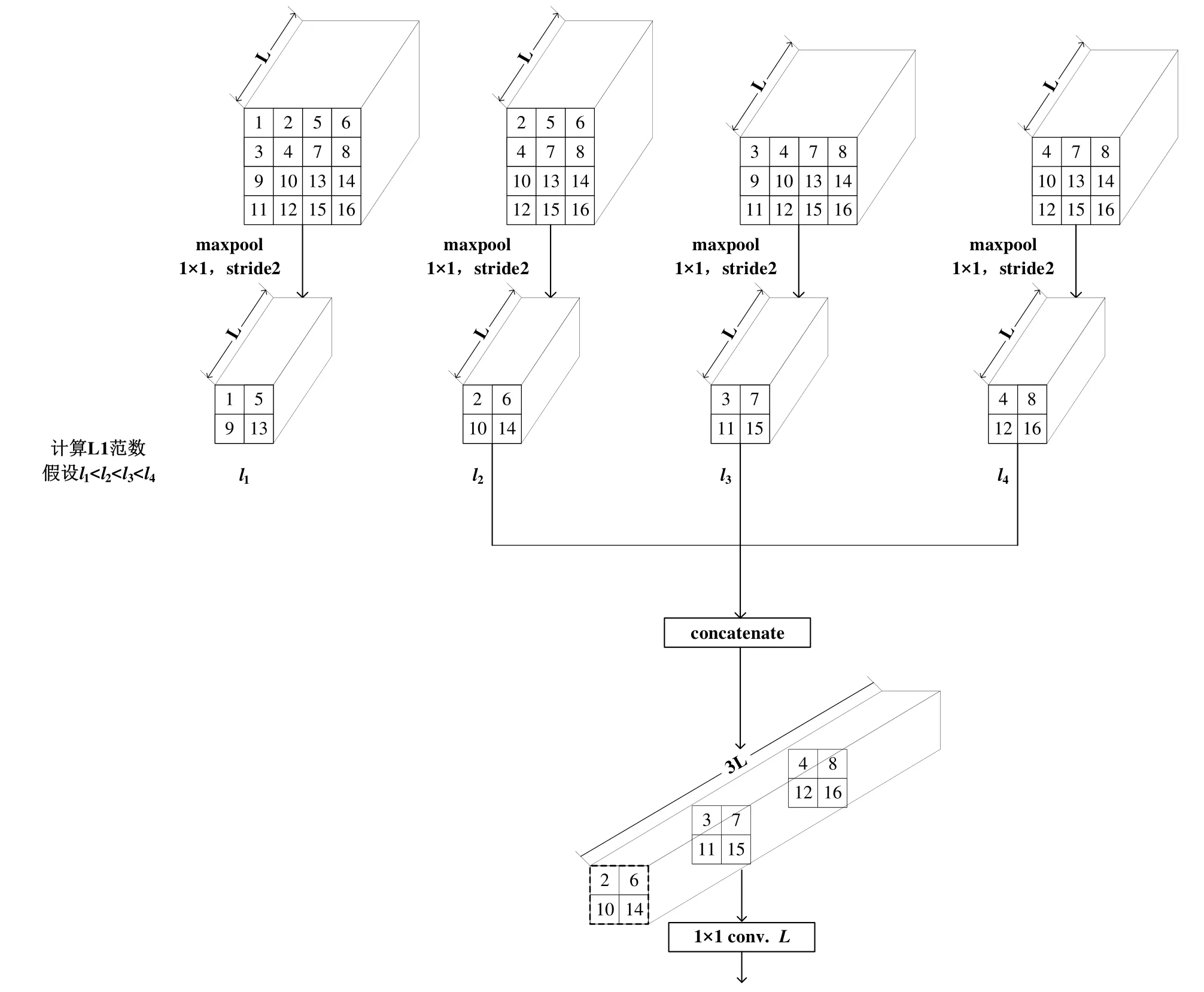
图2 基于L1范数的降采样方法的tensorflow实现示意图Fig.2 The diagram of tensorflow implementation of the down-sampling method based on L1 norm

表1 实验使用的卷积神经网络的结构Tab.1 The structure of the convolutional neural networks used in experiments

3.1 CIFAR-10数据集上的实验结果

CIFAR-10数据集包含10类物体的图像，每类物体有6000张图片，50000张用于训练，10000张用于测试，图像尺寸为32×32。实验使用了数据增强（data augmentation）技术，包括随机剪切、左右翻转、调整亮度、调整色调、调整饱和度和调整对比度。随机剪切时从原图像中随机截取28×28的连续像素区域。归一化数据增强后的图像作为神经网络的输入。训练方法采用最小批梯度下降法（Mini Batch Gradient Descent），使用交叉熵函数作为损失函数，每批训练数据包含50张图片。采用Xavier[14]方法对参数初始化，每层神经网络的参数按照下列均匀分布进行初始化：

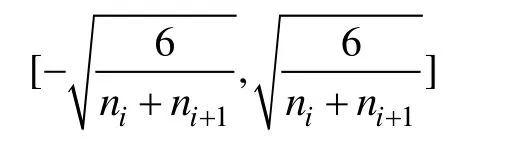
其中，ni表示当前层神经网络的参数量，ni+1表示下一层神经网络的参数量。参数更新采用Adam方法[15]。训练总迭代次数设置为300000次。为了比较不同卷积神经网络的性能，将四个网络分别进行三次实验，每次实验包括一个训练过程和一个测试过程。

表2 硬件平台主要元件的规格型号Tab.2 Specifications of the main components of the hardware platform

表3 CIFAR-10数据集上的平均分类准确率（单位：%，使用了数据增强）Tab.3 The average classification accuracy on CIFAR-10 datasets. (Unit: %, with data augmentation)

表4 卷积神经网络的参数量（单位：百万）Tab.4 The number of parameters of the convolutional neural networks. (Unit: million)

所有神经网络的平均分类准确率如表3所示，参数量如表4所示。平均准确率是三次实验结果的平均值。从表3可以看到，分类准确率最高的神经网络是 FS-CNN，L1-CNN的分类准确率低于FS-CNN、高于MP-CNN。表4给出了所有神经网络的参数量，FS-CNN与 MP-CNN的参数量相同，L1-CNN的参数量略少一些。从表3和表4中可以看出，当输入的四分之一被丢弃时（L1-CNN(k=3)），分类准确率与输入全部保留时（FS-CNN）相比下降了 0.49%，当输入的四分之二被丢弃时（L1-CNN(k=2)），分类准确率继续下降，与丢弃四分之一输入时相比下降了0.41%，已经与MP-CNN的分类准确率89.60%差别不大。这说明输入信息都是对分类“有用的”，尽管贡献大小可能不一样，丢弃的输入越多，对分类越不利。

3.2 MNIST数据集实验结果

MNIST数据集包含60000张手写体阿拉伯数字图片，训练集包含55000张图片，验证集包含5000张图片，测试集包含10000张图片。所有图片都是灰度图，尺寸为28×28。训练迭代次数为20000次，没有使用数据增强，直接把28×28原始灰度图片作为卷积神经网络的输入，实验所用的神经网络结构、训练方法和参数设置与 CIFAR-10相同。平均分类准确率如表5所示，MNIST上平均分类准确率的排名与CIFAR-10相同。因为MNIST相比CIFAR-10分类难度低，所以神经网络的分类准确率都比较高。因为MNIST实验所用的神经网络结构与CIFAR-10数据集相同，所以参数量与表4相差很小，故不再单独列出。MNIST实验也说明，与MP-CNN相比，FS-CNN和L1-CNN (k=3)使用了更多对分类“有用”的输入信息，从而提高了分类准确率因为大部分神经网络的平均分类准确率较高。

表5 MNIST数据集上的平均分类准确率（单位：%，没有使用数据增强）Tab.5 The average classification accuracy on MNIST datasets. (Unit: %, without data augmentation)

4 结束语

本文从卷积神经网络的降采样层入手，针对最大池化丢弃对图像分类“有用”的信息这一问题，提出了全采样方法和基于L1范数的降采样方法。分别保留全部输入和部分输入。在 CIFAR-10和MNIST上的实验表明，在神经网络结构相同、参数量也相同甚至更少的情况下，所提方法比最大池化的分类准确率高，说明使用的输入信息越多，分类准确率越高。

[1] 杨燕, 刘刚, 张龙. 基于2DPCA和LDA的人脸图像预处理与RBF神经网络的人脸图像识别研究[J]. 软件, 2014,35(2): 115-118.

[2] 王宏涛, 孙剑伟. 基于BP神经网络和SVM的分类方法研究[J]. 软件, 2015, 36(11): 96-99.

[3] 安大海, 蒋砚军. 基于BP神经网络的人脸识别系统[J]. 软件, 2015, 36(12): 76-79.

[4] 王新年, 张涛, 王海姣. 基于神经网络和先验知识的低分辨率车牌字符复原方法[J]. 新型工业化, 2011, 1(6): 78-83.

[5] A. Krizhevsky, I. Sutskever, and G. E. Hinton, Imagenet classification with deep convolutional neural networks[C],Advances in neural information processing systems, 2012:1097-1105.

[6] K. Simonyan, A. Zisserman, Very deep convolutional networks for large-scale image recognition[J], arXiv preprint arXiv: 1409. 1556, 2014.

[7] C. Szegedy, W. Liu, Y. Jia, et al, Going deeper with convo-lutions[C], Proceedings of the IEEE conference on computer vision and pattern recognition, 2015: 1-9.

[8] K. He, X. Zhang, S. Ren, et al, Deep residual learning for image recognition[C], Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.

[9] J. T. Springenberg, A. Dosovitskiy, T. Brox, et al, Striving for simplicity: The all convolutional net[J], arXiv preprint arXiv: 1412. 6806, 2014.

[10] 才云科技Caicloud, 郑泽宇, 顾思宇. TensorFlow: 实战Google深度学习框架[M]. 北京: 电子工业出版社, 2017.

[11] 山姆·亚伯拉罕著. 段菲, 陈澎译. 面向机器智能的TensorFlow实践[M]. 北京: 机械工业出版社, 2017.

[12] S. Ioffe, C. Szegedy, Batch normalization: Accelerating deep network training by reducing internal covariate shift[C], International Conference on Machine Learning,2015: 448-456.

[13] V. Nair, G. E. Hinton, Rectified linear units improve restricted boltzmann machines[C], Proceedings of the 27th international conference on machine learning, 2010: 807-814.

[14] X. Glorot, Y. Bengio, Understanding the difficulty of training deep feedforward neural networks[C], Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 2010: 249-256.

[15] 何宇健. Python与机器学习实战: 决策树、集成学习、支持向量机与神经网络算法详解及编程实现[M]. 北京: 电子工业出版社, 2017.