基于改进HMM的驾驶疲劳险态识别方法

张 明 恒， 翟 晓 娟， 朱 有 明， 赵 秀 栋

( 1.大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024； 2.大连理工大学 汽车工程学院, 辽宁 大连 116024 )

0 引 言

疲劳驾驶是引发高速公路交通事故尤其是重大交通事故的主要原因[1]．据美国高速公路安全管理局(National Highway Traffic Safety Administration，NHTSA)统计，在美国每年由疲劳驾驶引发约10万起交通事故，其中约1 500起导致直接死亡[2]．研究结果表明[3]，如果在危险发生前0.5 s对驾驶人进行预警，则可减少60%左右的碰撞交通事故发生．因此，在完全智能化的无人驾驶技术距离实际应用尚有差距的现阶段，研发车载预警辅助驾驶系统是满足市场需求、有效降低交通事故发生的可行途径．

驾驶疲劳险态辨识的本质，即是基于相关特征信息识别即将出现的危险状态，以及时提醒驾驶人或对车辆实施主动干预，其主要包括两方面：与疲劳形成相关的关键特征指标析取和依据相关指标对疲劳险态发生进行动态辨识．

特征指标的检测总体上可分为主观和客观两类方法．主观指标检测大多基于驾驶人主观感受的调查，统计分析疲劳险态的诱因，评测标准有皮尔逊疲劳量表[4]、斯坦福嗜睡量表[5]等．客观指标检测可分为两种：接触式和非接触式．其中，接触式方法以检测驾驶人脑电(electroencephalogram，EEG)、心电(electrocardiogram，ECG)等生理参数为主[6-9]．该类方法的优点是客观性强，能比较准确地反映驾驶个体精神状态的变化；但缺点也很明显，均需测量装置与驾驶人身体有关部位接触，这在很大程度上限制了其推广应用．基于上述研究局限性，研究人员试图从驾驶人外在表观指标推断驾驶安全性[10-13]．其中，卡内基梅隆研究所发现PERCLOS(percent eye closure)特征中的P80特征与驾驶疲劳程度的相关性最好[13]，这被NHTSA认可为驾驶疲劳监测的有效方法之一．

在疲劳险态辨识机理研究方面，所采用的模型主要包括贝叶斯网络[14-15]、神经网络[16-19]和隐马尔可夫模型(HMM)[20-21]等．综合来看，多特征信息融合已经成为该领域当前的研究热点和趋势，由于驾驶疲劳的产生是渐进的动态生成过程，利用HMM可以更好地反映该种特性变化．然而，受限于HMM参数优化过程的随机性及训练过程易陷入局部最优的问题，基于群集智能方法对相关参数进行优选是该领域较新的研究热点．

基于此，本文利用粒子群优化(PSO)算法对所构建的HMM驾驶疲劳辨识模型中的相关参数进行优选，以解决参数训练过程出现的相关问题，并结合模拟实验数据集对所提出的改进方法进行有效性对比验证．

1 问题描述

1.1 表征指标分析

为实现对险态的有效监测，首先需寻求能反映驾驶状态变化的关键特征．目前，PERCLOS特征已被证明为反映驾驶疲劳状态的最有效特征之一，其定义为单位时间内(一般取1 min或30 s)眼睛闭合一定比例(50%、70%或80%)的时间所占的比率[22]，包括P70、P80和EM共3个特征指标，分别表示眼睑盖过瞳孔的面积超过70%、80%和50%所占的时间比例．其中，P80特征已被证实与疲劳程度的相关性最好，因此在一些基于视觉的疲劳检测系统中一般采用P80作为疲劳识别的判据．其具体确定方法如图1所示．

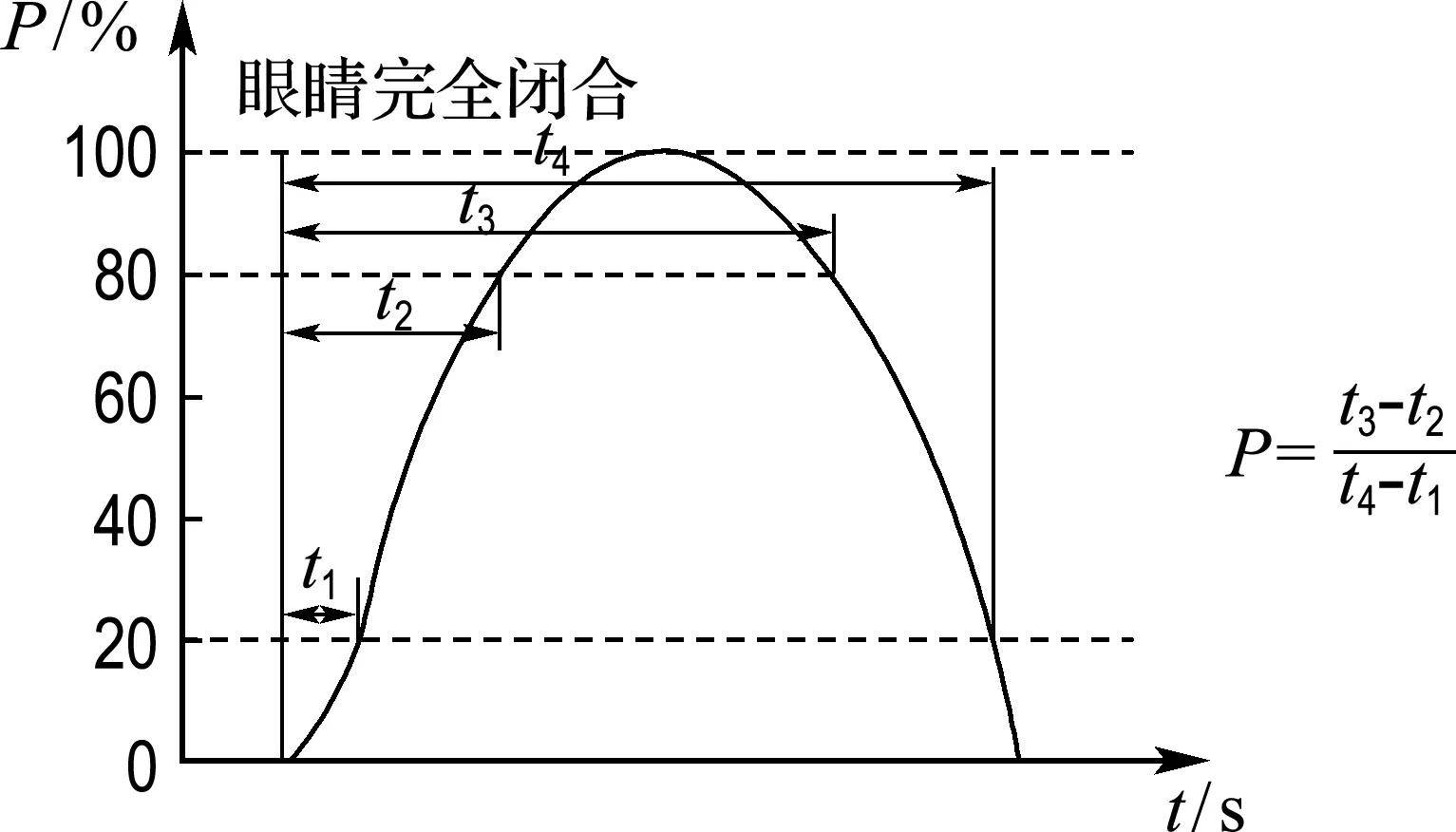
图1 PERCLOS指标(P80)示意图Fig.1 Schematic diagram of PERCLOS (P80)

1.2 HMM分析

典型HMM问题可简记为λ=(π，A，B)，即HMM由两部分组成：其一为马尔可夫过程，由初始概率矢量π和隐含状态转移概率矩阵A描述，它直观地反映了隐含状态序列的变化情况；其二为观察值随机过程，由混淆矩阵B描述，其输出为观察值序列．对于离散HMM问题，初始参数π、A对模型准确度影响不大，可随机分布或均匀分布，但需满足以下条件：

(1)

式中：aij为隐含状态从i转移到j的概率，P(qi=θi)为t时刻对应马尔可夫链上的状态q属于有限状态θ的概率．

对于混淆矩阵B，其初值的选取很大程度上会对最终模型准确度产生影响，分析其主要原因在于HMM训练过程所基于的BW算法[23]易陷入局部最优．因此，在具体实施时要求选取的初始B恰当才能使结果接近全局最优，这为HMM的实际应用带来了一定困难．目前，利用近年来发展起来的进化算法(evolutionary algorithm，EA)结合HMM训练过程对相关参数进行选优逐渐成为该领域的研究热点问题．考虑到EA中PSO算法实现容易、精度高、收敛快等优点，本文提出一种改进的BW-PSO算法分别对模型参数进行训练．其基本工作流程如图2所示．

图2 基于BW-PSO算法改进的HMM参数训 练流程Fig.2 Training diagram of improved HMM based on BW-PSO algorithm

BW-PSO算法的基本计算流程为

初始化：依据训练规模，随机生成n个A0和B0；

初值选取：对所有A0和B0分别基于传统BW算法训练得到更新后的n个A1和B1；

适应度函数：基于更新的所有A1、B1进行最大可能状态估计并得到对应的状态估值序列

Q＾

=(

q＾

1

q＾

2…

q＾

i)，i=1,…,n，则该状态估值序列与状态基准序列Q=(q1q2…qi)的差值为X=

Q＾

-Q，选择X的方差作为适应度判定准则，即

(2)

粒子位置和速度更新：通过比较每次更新后的适应度δ大小来调整粒子的位置和速度：

(3)

式中：r为随机数；微粒群体规模为N，其中每个微粒在D维空间中的坐标位置向量表示为xi=(xi,1xi,2…xi,d…xi,D)，速度向量表示为vi=(vi,1vi,2…vi,d…vi,D)，微粒个体最优位置(即该微粒经历过的最优位置)记为pi=(pi,1pi,2…pi,d…pi,D)，群体最优位置记为pg=(pg,1pg,2…pg,d…pg,D)．

终止条件：以充分保证算法收敛为原则，确定最大训练次数Tmax，当训练次数达到上限时，状态估计值对应的状态转移概率矩阵A和混淆矩阵B即为全局最优值．

此外，由于马尔可夫链状结构可以分为左右链型(left-right model)和各态遍历型(ergodic model)，所建立的HMM需针对实际问题进行相应选择．图3为一典型的各态遍历型结构，在该类HMM中，某一时刻可以处于任何状态，并且都能在有限次数的转移后处于马尔可夫链中的其他任何状态．而左右链型规定了随着时间的变化状态向原状态转移，或者向规定大序号状态转移，该类HMM能够更有效地应用到各种随时间变化的参数数据建模，如语音信号识别、驾驶疲劳险态的生成等．

图3 各态遍历型HMM结构Fig.3 Ergodic model of HMM

1.3 HMM验证

吻合度分析是验证模型准确性的关键．在本研究中，利用优化后的HMM推理得到最可能状态序列

Q＾

，基于该序列结合状态基准序列Q来验证模型的准确性．其中，状态基准序列是根据生理参数测试仪、基于视频客观评价以及主观打分3种方式获得．吻合度分析包括以下两方面：

(1)计算状态估值序列

Q＾

与状态基准序列Q的相似度百分比．对于序列长度为N的情况，若两序列中的状态重合数为s，则相似度Si定义为

(4)

(2)计算状态估值序列

Q＾

X=Q＾-Q，V=∑ni=1Xi/N，

与状态基准序列Q差值向量X的方差．定义则其方差

(5)

2 驾驶疲劳险态HMM构建

2.1 特征参数预处理及HMM转移模型确定

基于已有研究结果[24]，本研究将HMM状态数定为两级：清醒和疲劳．与此相对应，各观测变量也分为两类，即数据正常或异常．基于文献[25]研究结果，这里设定PERCLOS的阈值为0.15，则特征参数经阈值处理后如表1所示．

表1 特征参数的二值化Tab.1 Characteristics parameters binary

由于HMM结构可分为左右链型和各态遍历型，考虑实际疲劳形成为一渐进的动态生成过程，该规律符合左右链型结构的本质特征．然而，由于本文仅定义了两种状态水平，从HMM各态遍历型的结构拓扑图上可以看出，此时各态遍历型退化为左右链型结构，由此本文将该研究的基本HMM划分为各态遍历型结构．基于以上分析，本文所建立的HMM结构如图4所示．

图4 马尔可夫链示意图Fig.4 Schematic diagram of Markov chain

2.2 HMM构建

在进行HMM构建时，鉴于初始模型参数的选取对于模型训练和最终准确度影响较大，本文对关键性参数概率矩阵A和混淆矩阵B的初始取值作如下考虑：

(1)由于矩阵A的初值对模型训练结果影响不大，只需满足式(1)的要求即可，这里考虑为均匀分布或随机分布．

(2)为方便后续对所提出的BW-PSO算法进行对比分析，这里依据有无先验条件对矩阵B的初值选取分两种情况，即随机分布和有先验条件分布．先验条件可描述为定义规定时段内的PERCLOS观察值序列长度为N，对其阈值化处理后的状态为M，状态基准序列为Q．利用数理统计方法统计出该时段内基准状态为j的个数Qj，观测值状态为i的个数Mi，则矩阵B中的各元素取值为

(6)

(3)对于BW-PSO算法，矩阵A、B的初值选择为随机分布．

基于以上分析，所建立的3个基本HMM参数如表2所示．

表2 各模型初值选取汇总表Tab.2 Summary sheet of all models′ initial values

3 参数优化

利用BW算法对HMM进行训练时，在模型参数初始值选定基础上利用式(7)进行反复迭代，最终通过转移概率估计值进行评估，直到矩阵A和B达到最优解．

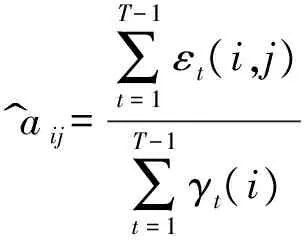
a＾ij=∑T-1t=1εt(i，j)∑T-1t=1γt(i)

b＾j(k)=∑Tt=1，ot=kγt(j)∑Tt=1γt(j)

(7)

在利用PSO算法对HMM参数寻优时，把BW-PSO算法结合后嵌入HMM，不需对初始参数A、B进行特别选取，只需随机选取，在不断的优化过程中即可达到全局最优．具体PSO算法的内部参数设定如表3所示．

表3 PSO算法参数Tab.3 Parameters of PSO algorithm

基于上述参数设定，整个训练过程各参数的收敛曲线如图5所示，横坐标β为迭代次数，寻优过程计算时间统计及最终参数优化结果如表4、5所示．其中，在图5中，考虑到矩阵A和B每行元素总和为1，故只选取第一列元素进行比较，即只选取A矩阵中的元素a11和a21，B矩阵中的元素b11和b21．

对上述参数优化过程及统计结果进行分析，可得以下结论：

(1)矩阵A各参数的迭代收敛过程一致．初值选取对模型训练精度影响不大，但基于先验知识和PSO策略的初值选定方法可在一定程度上加快训练进程．

(2)矩阵B各参数的迭代收敛过程差别较大．随机选定初值时，模型易陷入局部最优，导致最终训练结果出现较大误差；基于先验知识和PSO策略的初值选定方法各参数的迭代变化过程一致，但PSO方法可以在一定程度上加快训练进程．

(a) 矩阵A参数优化过程对比曲线

(b) 矩阵B参数优化过程对比曲线

图5 矩阵A、B参数优化过程Fig.5 Optimizing process of matrix A and B

表4 3个模型参数寻优计算时间Tab.4 Parameter optimizing time of three models

(3)基于先验知识和PSO策略的初值选定方法可有效减少模型训练迭代次数，但由PSO引入所带来的计算时间复杂度较其他方法要大得多．由此可见，对于小规模复杂问题，基于BW-PSO算法的模型训练方法尚可接受，但随着问题复杂度的增大，需在其计算成本与计算精度间进行折中．

(4)基于BW算法的模型训练结果准确性严重依赖于矩阵B的初始估值，基于先验知识和PSO策略的方法具有较稳定的模型训练结果准确性；但由于先验条件的引入，其条件策略设定需针对不同问题进行具体制定，不利于算法的自动化实现；基于PSO策略的方法除具有较稳定的结果输出外，由于不需人为制定相应条件规则，更有利于实现算法的智能化．

表5 优化后的各模型参数Tab.5 Parameters of all the optimized models

4 实证分析

4.1 实验数据

为比较上述所建立模型在疲劳险态识别上的差异，进行了数据测试．招募了20名年龄段在24～26岁且驾龄在2～3 a的驾驶人，对每名实验者以1 min为单位用SMI-HED头盔式眼动仪在驾驶模拟器上获取相应的PERCLOS特征观察值序列，原始数据序列时长为3 h．为降低模型计算复杂性，从中抽取具有代表性的20组长度为30的样本进行建模，其特征参数时序变化曲线如图6所示．

图6中，阈值线以上为驾驶人疲劳状态采样数据，以下为清醒状态采样数据．从曲线变化趋势来看，在选定时段内驾驶人经历了“疲劳-清醒-疲劳-清醒-疲劳-清醒”的状态转变，可以用于验证所建模型的准确性．

图6 PERCLOS曲线图Fig.6 Curve graph of PERCLOS

4.2 结果对比分析

4.2.1 模型稳定性分析 对于模型1和模型3，随机选取10组不同的初值进行稳定性验证；由于模型2是模型1的特例(模型1先验条件下的输出)，从20组样本数据中抽取10组进行先验统计得到10组初值后，再统一和模型1以及模型3进行稳定性比较．模型的具体准确度稳定性分析对比结果如图7所示，横坐标η为初值选取次数．

图7 3个模型准确度对比图Fig.7 Contrast diagram of the change of three models′ accuracy

由此可见，模型1准确度变化曲线起伏最大，稳定性最差；模型2相比于模型1稳定性较好，但相对模型3也存在一定差距．

4.2.2 模型准确性分析 考虑到3个模型各自对初值选取的不同要求以及随机初值的重要性，本文分别从1次初值选取和10次随机初值选取两方面验证3个模型的准确性：

(1)在实验时段内，3个模型得到的最可能状态序列与状态基准序列的比较如表6所示，基准状态为

表6 各模型误判次数统计Tab.6 Statistics of all the models′ mistakes

由表6可知，模型1输出结果与基准状态有较大差别，准确率与稳定性最差；模型2输出结果与基准状态差别较小，准确率与稳定性较好；模型3较模型1和2准确率及稳定性要好，与基准状态吻合度较高．

(2)随机选取10个不同初值以验证3个模型的整体准确度，其对比结果如图7所示．可见：模型1的准确度起伏在10.0%～76.7%，仅在第3次和第7次初值选取时，达到了较高的76.7%和73.3%；模型2的准确度起伏在66.7%～76.7%，整体准确度相比于模型1高；模型3的准确度起伏在76.7%～83.3%，模型整体准确度高于前两个模型．

5 结 语

在HMM应用过程中，混淆矩阵的初值选取对于模型最终准确性有较大影响．本文在对驾驶疲劳险态动态生成特性分析基础上，提出利用改进的BW-PSO算法对所建立的HMM进行训练，以克服实际应用过程中面临的困难．与传统BW算法的结果对比分析表明，本文所提出的方法无须考虑HMM初值的选取即可达到全局最优，省略了复杂的初始参数运算估计，较BW算法具有更高的准确性和稳定性．基于已取得的研究成果，下一阶段应从多源信息融合角度对所建立的模型进行拓展，以进一步提高模型的适用范围和鲁棒性．

[1] 孟宪超. 疲劳驾驶致交通事故特点及有效预防分析[J]. 物流工程与管理, 2014,36(8):187-188.

MENG Xianchao. Driving fatigue caused by traffic accident characteristics and effective prevention analysis [J].LogisticsEngineeringandManagement, 2014,36(8):187-188. (in Chinese)

[2]李都厚,刘 群,袁 伟,等. 疲劳驾驶与交通事故关系[J]. 交通运输工程学报, 2010,10(2):104-109.

LI Duhou, LIU Qun, YUAN Wei,etal. Relationship between fatigue driving and traffic accident [J].JournalofTrafficandTransportationEngineering, 2010,10(2):104-109. (in Chinese)

[3]WANG C D, THOMPSON J P. Apparatus and method for motion detection and tracking of objects in a region for collision avoidance utilizing a real-time adaptive probabilistic neural network: U. S. Patent 5613039 [P]. 1997-03-18.

[4]CARROLL R J. Ocular measures of driver alertness: FHWA Technical Report No. FHWA-MC-99-136 [R]. Washington D C: Federal Highway Administration, 1999.

[5]HODDES E, ZARCONE V, SMYTHE H,etal. Quantification of sleepiness:a new approach [J].Psychophysiology, 1973,10(4):431-436.

[6]DA SILVEIRA T L T, KOZAKEVICIUS A J, RODRIGUES C R. Automated drowsiness detection through wavelet packet analysis of a single EEG channel [J].ExpertSystemswithApplications, 2016,55:559-565.

[7]SAN P P, LING S H, CHAI R,etal. EEG-based driver fatigue detection using hybrid deep generic model [C] //ProceedingsoftheAnnualInternationalConferenceoftheIEEEEngineeringinMedicineandBiologySociety,EMBS. Orlando: IEEE, 2016:800-803.

[8]BORGHINI G, ASTOLFI L, VECCHIATO G,etal. Measuring neurophysiological signals in aircraft pilots and car drivers for the assessment of mental workload, fatigue and drowsiness [J].NeuroscienceandBiobehavioralReviews, 2014,44:58-75.

[9]付荣荣,王 宏,张 扬,等. 基于可穿戴传感器的驾驶疲劳肌心电信号分析[J]. 汽车工程, 2013,35(12):1143-1148.

FU Rongrong, WANG Hong, ZHANG Yang,etal. An analysis on EMG and ECG signals for driving fatigue detection based on wearable sensor [J].AutomotiveEngineering, 2013,35(12):1143-1148. (in Chinese)

[10]MITTAL A, KUMAR K, DHAMIJA S,etal. Head movement-based driver drowsiness detection:A review of state-of-art techniques [C] //Proceedingsof2ndIEEEInternationalConferenceonEngineeringandTechnology,ICETECH2016. Coimbatore: IEEE, 2016:903-908.

[11]ANIL P C, ARAVIND B, SARITHA S,etal. Development of a headband for acquisition and analysis of forehead EOG signal for driver fatigue detection based on eye-blink patterns [J].InternationalJournalofComputerApplications, 2014,96(23):42-46.

[12]SIGARI M H, POURSHAHABI M R, SORYANI M,etal. A review on driver face monitoring systems for fatigue and distraction detection [J].InternationalJournalofAdvancedScienceandTechnology, 2014,64(5):73-100.

[13]DINGES D F, GRACE R. PERCLOS: A valid psychophysiological measure of alertness as assessed by psychomotor vigilance [R]. Washington D C: Office of Motor Carriers, Federal Highway Administration, 1998.

[14]王连震,裴玉龙. 基于贝叶斯网络的驾驶疲劳程度识别模型[J]. 城市交通, 2014,12(3):66-74.

WANG Lianzhen, PEI Yulong. Driving fatigue recognition model based on Bayesian network [J].UrbanTransportofChina, 2014,12(3):66-74. (in Chinese)

[15]GUO Wenqiang, ZHANG Baorong, XIA Lingjun,etal. Driver drowsiness detection model identification with Bayesian network structure learning method [C] //Proceedingsofthe28thChineseControlandDecisionConference,CCDC2016. Yinchuan: IEEE, 2016:131-136.

[16]TABAL K M R, CALUYO F S, IBARRA J B G. Microcontroller-implemented artificial neural network for electrooculography-based wearable drowsiness detection system [J].LectureNotesinElectricalEngineering, 2016,362:461-472.

[17]YAN Chao, JIANG Huiying, ZHANG Bailing,etal. Recognizing driver inattention by convolutional neural networks [C] //Proceedings—20158thInternationalCongressonImageandSignalProcessing,CISP2015. Shenyang: IEEE, 2015:680-685.

[18]SINGH A, KAUR J. Driver fatigue detection using machine vision approach [C] //Proceedingsofthe20133rdIEEEInternationalAdvanceComputingConference,IACC2013. Washington D C: IEEE Computer Society, 2013:645-650.

[19]KRISHNASREE V, BALAJI N, SUDHAKAR RAO P S. A real time improved driver fatigue monitoring system [J].WSEASTransactionsonSignalProcessing, 2014,10(1):146-155.

[20]FU Rongrong, WANG Hong, ZHAO Wenbo. Dynamic driver fatigue detection using hidden Markov model in real driving condition [J].ExpertSystemswithApplications, 2016,63:397-411.

[21]XIANG Yu. Eye fatigue state recognition of Gabor wavelet optimization HMM algorithm [J].InternationalJournalofHybridInformationTechnology, 2016,9(9):189-198.

[22]BAUM L E, PETRIE T, SOULES G,etal. A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains [J].TheAnnalsofMathematicalStatistics, 1970,41(1):164-171.

[23]ELMEZAIN M, AL-HAMADI A, APPENRODT J,etal. A hidden Markov model-based continuous gesture recognition system for hand motion trajectory [J].Proceedings—InternationalConferenceonPatternRecognition, 2008:4761080.

[24]DESMOND P A, HANCOCK P A. Active and passive fatigue states [M] // PA H, PA D, eds.Stress,WorkloadandFatigue. Mahwah: Lawrence Erlbaum Associates, 2001:455-465.

[25]郭永彩,李文涛,高 潮. 基于PERCLOS的驾驶员疲劳检测算法[J]. 计算机系统应用, 2009,18(8):54-57.

GUO Yongcai, LI Wentao, GAO Chao. Fatigue detection algorithm based on PERCLOS [J].ComputerSystems&Applications, 2009,18(8):54-57. (in Chinese)