Excel 中地学矢量数据处理方法探讨

秦 红

（上海市青浦区水文勘测队，上海 201799）

1 问题的提出

与地学有关的诸多问题，都涉及到对矢量的分析，比如水文学中水流的流速流向、气象学中的风速风向、海洋学中的海流和波浪等。对矢量的研究，除了要分析其大小变化特征，还要分析其方向变化特征。因此矢量分析是地学研究中非常重要又相对较难的内容。

随着监测和信息技术的快速发展，大范围在线连续监测得以广泛应用，并因而产生了大量的数据需要处理。计算机技术大大提高了数据处理的效率，但也存在着一些问题。在对矢量数据的处理上，因坐标系定义的不同，常常引起一些不必要的困惑和麻烦。以日常工作中常用的数据处理软件Excel 为例，该软件的坐标系实质上是数学坐标系，在处理矢量数据时，以X轴正方向（地理意义上的正东方向）作为角度起点，沿逆时针方向角度逐渐增大。但地理坐标系的角度，是以Y轴正方向（地理意义上的正北方向）作为起点，沿顺时针方向逐渐增大。二者之间存在明显的差别。

上述问题其实是坐标系转换的问题。有关坐标系转换的研究，国内外开展比较多，但绝大多数都集中在不同投影坐标系如高斯—克吕格、通用横轴墨卡托、兰勃脱等投影相互之间的转换[1–5]，以及这些投影坐标系与大地坐标系之间的换算上[6–9]。但是对于地理与数学坐标之间关系的研究和数据处理方法，却鲜有涉及。那么，如何利用 Excel 等软件来处理地学中的矢量数据，使之符合要求呢？这正是所要解决的问题。

2 通过分量获得矢量地理角度

2.1 对应关系

地理和数学坐标，由于起算点不同，旋转的方向相反，存在着较大的差别。以几个特殊角度为例，有表 1 和图 1 所示的对应关系。

2.2 对应关系

从图 1 可以看出，地理和数学坐标存在着严格意义上的分段线性对应关系，只是在数学角度 90°这个位置产生了跃变。

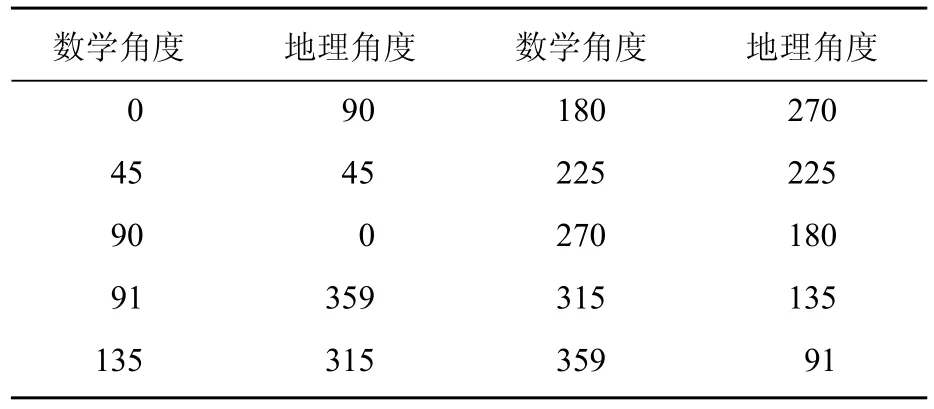
表 1 地理与数学角度的对应关系 （°）

图 1 地理与数学角度对应关系图

进一步分析它们之间的分段对应关系可知，设数学坐标系角度为X，地理坐标系角度为Y，则有：

2.3 用 Excel 进行角度转换

ADCP 测量获得的流速通常以东向x、北向y和垂向z的 3 个分量表示。如果不考虑垂线流速分量，只考虑东向和北向分量的话，那么水平方向上合成流速的角度α可以先通过以下 Excel 内置的公式计算：

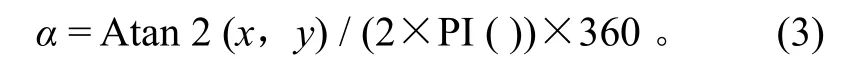
式 (3) 中 Atan 2 (x，y) 是根据东向和北向流速分量计算出来的数学坐标系的流向，单位为弧度，需要通过弧度和角度的关系转换成度。由于 Excel 软件本身的特征，式 (3) 中计算出的角度，当 ＞180° 时就变成了负值。必须通过下面的判别函数，再转换为真正的数学坐标系的流向角度A数：

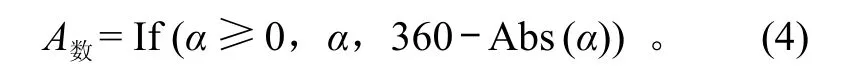
将数学坐标系的流向计算出来以后，再根据上式 (1) 和 (2) 中地理和数学坐标系之间的换算关系，通过 Excel 的判别函数，计算出最终所需的地理坐标系流向角度值A地：

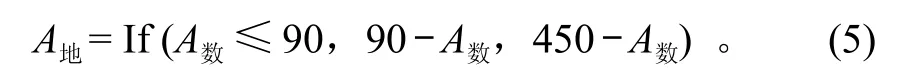
以上式 (3)，(4)，(5) 还可以通过嵌套判别的方法，直接计算出最终流向角度值。

2.4 计算实例

以 2015 年 5 月长江口科研调查中 ADCP 测验成果为代表，根据东向、北向流速值，通过 Excel 计算各水层水流流向角度，结果如表 2 所示。计算结果与ADCP 显示的垂线平均流向角度相比较，是一致的，说明本文所提供的方法是正确、可行的。

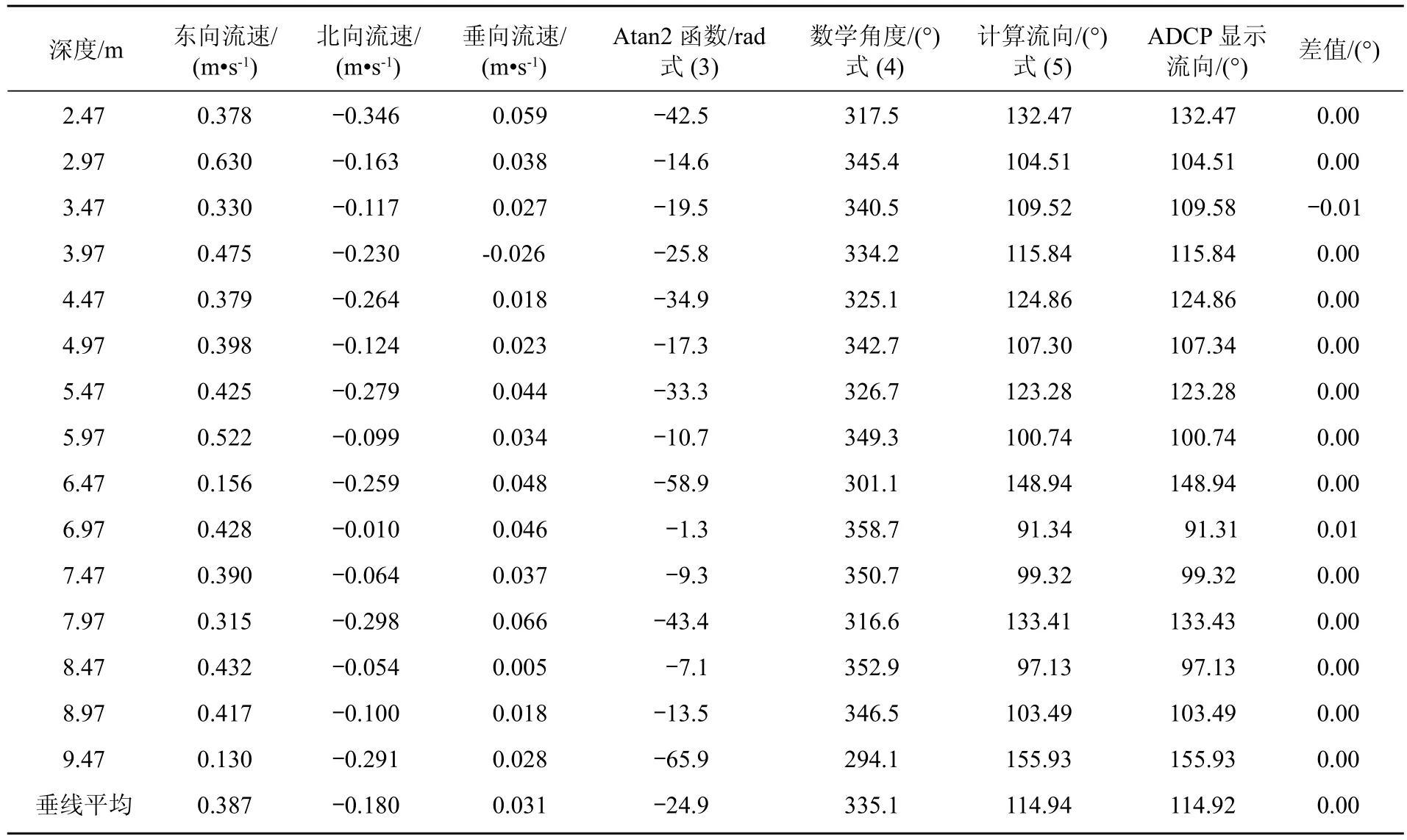
表 2 实测资料计算实例

3 通过矢量角度获得各向分量

3.1 计算方法

前文论述了用 Excel 如何通过地学矢量的各向分量来计算其地理坐标角度，即该矢量的方向。那么，如果知道地学矢量的大小和角度，如何计算其在北向和东向的分量呢？

由于 Excel 默认的坐标系为数学坐标系，地学矢量数据中的角度在 Excel 中会被“误认为”是数学意义上的角度，即以x轴正方向为起算点，沿逆时针方向增大。由于坐标系的不同，计算过程中会遇到问题，出现北向和东向分量值相互颠倒的错误结果。比如，正北方向的风，风速为 9.5 m/s，风向为 0°，按照地学意义上的理解，北向（对应数学坐标系的y轴）的风速分量应为 9.5 m/s，东向（对应数学坐标系的x轴）的风速分量应为 0 m/s。但是按照通常的方法，在 Excel 中求y轴的分量应该用正弦函数，求x轴的分量应该用余弦函数。如果这样直接计算，则北向的风速分量变成 0 m/s，而东向的风速分量变成9.5 m/s，这显然是不对的。

经过试验发现，如果用余弦函数直接计算矢量数据的北向分量，用正弦函数直接计算矢量数据的东向分量，能够得到完全正确的结果。

3.2 计算实例

利用 Excel 软件，以长江口某站 2014 年 2 月每天上午 8 时的风速风向资料为例，通过上述方法计算各向风速，结果如表 3 所示。计算结果表明，用该方法在 Excel 中计算地学矢量的各向分量，与用数学解析方法计算的结果一致。说明该方法是可行的。

4 结语

由于数学和地理坐标系之间的差异，在使用诸如 Excel 等数据处理软件分析计算地学中的流速流向、风速风向等矢量数据时，要特别注意在处理角度数据时坐标系之间的这种差异，不能盲目地直接计算，否则会得到匪夷所思的结果。

数学和地理坐标系之间的转换关系虽然比较简单，但是在各种分析计算过程中经常用到，具有较大的实用性。将这种关系应用到 Excel 的实际数据处理过程中，得到了正确的结果。这种方法在其它类似的数据处理软件中也能得到较好的应用。

表 3 长江口某站风速风向资料计算实例

[1] 李冰峰，陈华荣，王显金. 利用 Excel 实现不同坐标系间的坐标转换[J]. 地矿测绘，2007，23 (3): 13-16.

[2] 杨战辉，韩东明. 浅谈 ARCGIS 中地图投影和坐标换算[J]. 测绘技术装备，2014，16 (4): 69-70.

[3] 顾秀梅，杨斌，高德政，等. ArcGIS 空间数据投影坐标转换方法研究[J]. 测绘科学，2012，37 (4): 164-166.

[4] 赵远. 国际工程中 UTM 投影与高斯投影的转换研究[J].有色金属文摘，2016，31 (1): 180-181.

[5] 盛业华，韩国建，郭达志. 地理信息系统中多种投影转换的实现[J]. 江苏测绘，1996 (1): 7-11.

[6] 高德章. 大地坐标系与投影坐标系[J]. 物探化探计算技术，2011，33 (1): 51-55.

[7] 方杨. 任意带任意投影面的平面坐标转换方法研究[J]. 铁道勘察，2011 (3): 18-20.

[8] 刘延斌，凡春明，陈永立. 投影变形对坐标转换精度的影响[J]. 测绘与空间地理信息，2014，37 (7): 184-186.

[9] 侯国超，刘蜀，杨琳. 墨卡托投影三维动态坐标转换方法研究[J]. 舰船电子工程，2017，37 (3): 44-45，130.