一种MEMS可重构群时延均衡器的设计

贾世旺，赵 飞

(中国电子科技集团公司第五十四研究所，河北 石家庄050081)

0 引言

随着各类装备要融入网络信息体系的要求，航天测控、卫星通信和导航等综合射频系统对低轮廓有源相控阵天线需求越来越迫切，同时系统对射频信道引入的非线性相位(群时延)失真也非常关注。文献[1]分析了全频谱合成阵列天线T/R组件间群时延失真分布差异性对合成信噪比的影响，研究结果表明：天线阵元数量越多，带宽越宽，群时延分布差异性越大，合成信噪比损失越大。文献[2]分析了卫星通信转发器群时延特性对传输性能的影响，当转发器工作带宽为36 MHz时，由于信道群时延波动，造成信道的Eb/N0传输性能恶化0.5 dB以上。文献[3]针对阵列天线设计出一种新型负群时延电路结构，有效提高了工作带宽；文献[4]对负群时延电路进行了研究，提出了多种工作频段为3 GHz左右的电路，电路工作带宽400 MHz，调整范围7.4 ns；文献[5]设计了一种利用有源FET管结合巴伦结构实现的3.5～5.5 GHz新型负群时延电路；文献[6]采用环行器与波导加载谐振腔级联设计的Ku频段群时延均衡器，群时延调整范围达到10 ns。

本文对S频段群时延均衡网络开展研究，并结合微纳工艺加工技术特点，提出了一种利用MEMS工艺技术制造的小型化新型全通网络电路结构方案，实现了群时延均衡器可重构设计。

1 全通网络

群时延表示系统在某频率下相位对频率的负微分，表达式为：

(1)

群时延失真会使传输信号的波形失真，增加系统误码率，降低系统性能。为了改善传输信道性能，常采用增加群时延均衡器对系统相移失真进行补偿和调节的办法。

群时延均衡器一般采用全通网络实现，理想的全通网络应具备以下特点：

① 网络输入/输出的幅度变化与传输的信号频率无关，幅度不随频率变化而改变；

② 网络输入/输出相位变化与频率的关系是一条过原点直线，相移随着频率的改变而变化。

全通网络理论上是一个无幅度失真网络(全频范围内)，理想桥型全通网络结构如图1所示。

图1 全通网络结构

图1中，Zc为传输网络特性阻抗，与Z1、Z2之间的关系如下：

(2)

(3)

(4)

式中，g0为传输常数，由固有衰减a0和固有相移b0组成；Z1、Z2分别由纯电抗元件X1、X2组成，且为了满足全通网络的构成条件，X1、X2必须异号[7]。

当X1、X2异号时，固有衰减a0为零，固有相移b0则与比值有关，全通网络的输入输出阻抗Zc为纯电阻阻抗R。

(5)

2 发射组件群时延特性

发射组件由放大器、移相器、衰减器、滤波器及延时线等元器件组成，其中放大器群时延特性变化一般在1 ns以下，衰减器和开关等群时延可忽略[8]，作为频率选择的滤波器，由于边带幅度变化大，导致群时延可达数十ns以上，对组件群时延贡献最大。矩形系数越高的滤波器，其群时延指标也越高。

某型号多路S频段发射组件群时延实测指标如表1所示。组件中滤波器采用矩形系数高、Q值高、带外抑制度特性好的六腔介质滤波器，此类滤波器具有群时延波动大的特点。

表1 某型S频段发射组件群时延实测结果

f2插损/dBf1群时延/nsf2群时延/nsf3群时延/ns1．7126．0311．8918．091．2726．2113．1421．561．3124．5513．7017．161．5227．0213．2119．271．3824．2515．6219．181．5625．0511．7120．871．8923．7912．8821．38

表1中，f1为滤波器低端截止频率；f2为中心频率；f3为高端截止频率。对表1中的数据进行统计分析可知，滤波器群时延特性差异明显，不同滤波器间群时延差异可以达到4 ns左右；高、低端频率与中心频率间群时延差异达到15 ns以上。

文献[1]理论分析表明：在100个阵列单元、1 GHz工作带宽的天线阵列系统中，当工作带宽高、低端边缘群时延差异大于4 ns时，合成信噪比将恶化0.5 dB以上。一般工程上要求群时延失真带来的合成信噪比损失要小于0.5 dB[9]，因此系统必须增加补偿网络，降低T/R组件高、低端频率群时延与中心频率群时延之间的差异。

为了改善信道的群时延特性需要完成两方面工作：一是调整高、中、低各频率间群时延的差异；二是调整不同信道间同频的群时延差异。因此，群时延均衡网络应满足谐振频率、群时延大小可重构要求。

考虑到S频段发射组件中元器件批次性差异，群时延均衡网络的群时延大小调整范围为5～20 ns，可均衡频率范围为2.40～2.65 GHz。

3 可重构均衡网络及元件实现

采用全通网络实现可重构均衡器设计，难点在于谐振频率、群时延大小可调的要求。必须对理想全通网络拓扑结构进行优化，增加可调元件。

3.1 新型可重构网络

根据微波理论，在全通网络中增加阻性元件，可以调整网络Q值大小，以增加网络插入损耗的办法，来实现群时延大小可调的目的。

在图1所示的电路基础上，提出了新型网络拓扑结构，同时为了便于与其他电路相连，将全通网络的平衡结构转换为不平衡的网络结构。图2是将理想全通网络转换为可重构的容抗二阶桥T型结构示意图，其中C1、L2、R1为可调元件。

图2 可重构容抗二阶桥T型结构

经分析，通过调节阻性元件大小，改变了L2、C3支路群时延特性，实现群时延大小可重构要求。可调电容C1、可调电感L2实现均衡网络频率的调整。

网络中的各元件参数的计算公式如下：

(6)

(7)

(8)

(9)

式中，R为二阶全通网络输入/输出阻抗；kn、ωn表示网络零极点实部及虚部的绝对数值。

若要实现可均衡频率2.40～2.65 GHz，调整群时延大小范围5～20 ns，结合图2网络拓扑结构，采用GENESYS软件对群时延网络进行分析，仿真结果如图3所示。

图3 单级群时延网络仿真结果

图3中，曲线fL最大值、fH最大值是指单级均衡网络单元可实现的群时延调整至最大值时的低端频率和高端频率；fL最小值、fH最小值是指单级均衡网络单元可实现的群时延调整至最小值时的低端频率和高端频率。单级均衡网络单元可实现频率2.38～2.84 GHz，群时延大小2～23 ns调整。

根据系统要求可采取多级级联的方式，增大群时延频率和大小调整范围。结合系统对均衡补偿网络的要求，采用三级二阶全通网络单元实现，三级均衡网络的谐振频率分别为：2.437 GHz、2.521 GHz和2.631 GHz。增加三级均衡网络，组件均衡后的群时延仿真结果见图3所示，频率调整范围大于450 MHz，调整群时延大小20 ns以上，发射组件均衡后在带内群时延波动小于2 ns。

三级均衡网络中可调元件取值范围：C1为7.0～10.2 pF、L2为18.7～24.2 nH、R1为0.1～20 Ω。

在理论分析时，电感、电容均假定为理想元件，实际电感还存在着电阻损耗、涡流损耗及介质损耗等；同样电容介质损耗和漏导等也不能忽略不计。由于各种损耗的存在，使得全通网络产生了与频率相关的衰减，而且输入输出的阻抗也不再是理想的纯电阻阻抗。

实现全通网络的电容、电感种类很多。为了保证性能，特别是降低网络带来的传输损耗，保证全通网络传输幅度不受影响，电路设计时应选择高Q值、高自谐振频率元件。部分文献中不同类型电感性能比较如表2所示。

表2 不同类型电感的性能比较

类型电感值/nH谐振频率/GHz品质因数绕线电感(高Q值)1～10002．020绕线电感(BondWire)[10]0．432．49-MEMS电感(Si)[11]2．724．236印刷电感(GaAs)[12]1．121．039印刷电感(PCB)[13]181．450薄膜电感(BCB)[14]6．27．948．5厚膜电感(LTCC)[15]13-30．6

根据不同类型L、C元件的优缺点，并考虑工艺实现难度及小型化要求，选择硅基MEMS的电感和电容来实现全通网络。MEMS元件是通过外部施加不同控制电压，静电驱动元件中可动结构，改变元件内部物理结构，实现了电感及电容的调节。

3.2 电感

采用MEMS工艺的3D螺旋电感具有体积小、易与其他元件集成的特点。为了实现电感可调，常采用分段切换开关、金属帽或者通过液体通道改变介质特性等不同方案。

图2中电感L2调整范围为18.7～24.2 nH，为了优化电感制作方案，采用固定感值电感与可调金属帽电感串联形式实现L2的可调范围。固定电感为16 nH，可调电感为2.7～8.2 nH。

S Mohan提出的基于Wheeler结论的公式是常用的平面螺旋电感计算方法[16]。

(9)

式中，μ为磁导率；n为螺旋电感圈数；dout、din分别为电感外径和内径；K1、K2分别为电感的结构因子，如表3所示。

表3 不同螺旋电感结构K1、K2值

螺旋电感结构类型K1K2方形2．342．75六边形2．333．82八边形2．253．55

固定和可调电感均选用方形结构，电感选用厚度为0.4 mm高阻硅(电阻率4 000 Ω· cm)，线宽20 μm，间距10 μm，线圈金属层厚度4 μm，内圈电极引线与平面螺旋线圈间增加聚酰亚胺材料进行绝缘。

由式(9)计算可知，固定电感线圈匝数为12.5圈，电感面积为0.8 mm×0.8 mm；可调电感匝数为3.5，面积为0.3 mm×0.3 mm。单位面积的电感密度大于20 nH/mm2，由于采用了MEMS加工技术，单个电感面积与普通PCB平面螺旋电感相比减小了80%以上，小型化效果明显，可调电感结构示意图如图4(a)所示。

利用MEMS工艺实现可调电感金属帽结构，通过施加控制电压，改变螺旋电感线圈与金属帽间距，影响磁通量和涡流的大小，使得等效电感值发生变化。

经软件仿真，可调电感金属帽与螺旋电感间距调整范围应满足10～50 μm，金属帽尺寸大小为250 μm×250 μm，可调电感仿真结果如图4(b)所示。

图4 MEMS可调电感结构示意及仿真结果

硅基衬底上生长一定厚度多晶硅和二氧化硅，溅射所需膜层，经过光刻、电镀及刻蚀制作螺旋电感；利用厚胶工艺在电感结构表面涂覆光刻胶，再次溅射、光刻、电镀和刻蚀，完成金属帽加工；最后进行可动结构释放，去除电感与金属帽间光刻胶，完成可动结构梁的制造。

为了提高电感性能，可以考虑采用MEMS硅腔刻蚀技术，制作悬浮螺旋电感结构，即螺旋电感上、下面均为空气介质，进一步降低电感与基板间涡流；也可增加新型磁性高分子材料膜层，通过提高磁导率的办法，提升单位面积电感密度。

3.3 电容

实现可调电容的方式有多种，常用的有变容二极管、MEMS可动结构等。

采用MEMS方式实现的可变电容具有噪声低、损耗小及可调范围大的特点，MEMS可调电容示意图如图5(a)所示。

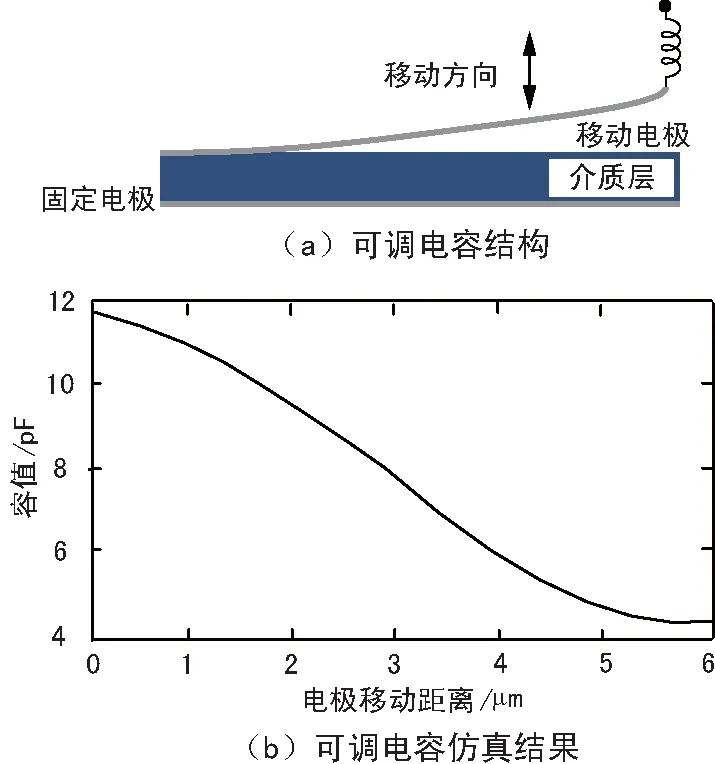
图5 MEMS可调电容结构及仿真结果

MEMS可调电容是通过固定电容一端电极，另一电极设计成悬浮结构，施加电压由静电驱动调整两电极间间距。用MEMS可动梁制造工艺完成移动电极的制作，通过调节两电极间距，实现容值调整。

电容调整范围要求为7.0～10.2 pF，采用硅基衬底上MIM(Metal-Insulator-Metal)电容实现，MIM电容由金属—绝缘体—金属3层结构组成，将上层的金属结构改为可垂直移动结构。

当MIM电容尺寸小于工作频率0.1 λ时，容值大小可由式(10)计算得出：

(10)

式中，εrd为电容材料的介电常数；w、l、d分别为电容的宽、长、高，单位μm。

当电容的长宽均为2 000 μm、介质层的厚度为35 μm时，硅基上实现的MIM电容的最大容值为12.04 pF，大于10.2 pF的要求。

将电容模型带入软件进行仿真分析，仿真结果如图5(b)所示。当电容上电极在原始锚点时，电容值为11.8 pF；当施加外部电源，电极移动6 μm时，电容值为4.2 pF，满足了均衡网络对可调电容的要求。

MEMS可调电容的工艺制作过程与电感类似。通过工艺控制，保证可动结构一致性是工艺制造的难点。

3.4 方案可行性

经过以上计算分析，带阻性可调元件的新型全通网络能够实现均衡器的可重构要求。采用MEMS工艺实现可调电感、可调电容的方案可实现性强。

采用传统集中元件，实现该三级全通网络体积不小于90 mm×55 mm×15 mm。采用MEMS元件的电路体积小于30 mm×15 mm×3 mm，小型化效果显著。由于MEMS元件的调整是通过电压来控制，对均衡器的电性能调整，该方案更加合理和实用。

在实际电路应用时，还要考虑以下问题：

① MEMS可调元件与固定值元件相比，制造复杂程度大，设计全通网络时应尽可能减少可调元件数量；

② 若全通网络的元件值取值不合适，易引起电路谐振，恶化电路性能，因此在确定元件值时要考虑温度、振动等外部环境条件对MEMS可动结构的影响，并进行敏感性统计分析；

③ 对于非理想元件组成的全通网络，接入电路后会产生一定损耗，需要增加放大电路进行增益补偿。

4 结束语

以全通网络理论为基础，优化电路网络结构，增加了阻性可调元件，实现了群时延补偿网络可重构的要求。提出了用MEMS工艺技术实现可调元件制造的思路，并对MEMS电感、电容等进行了设计仿真分析，均衡器小型化效果明显。

MEMS工艺适用于群时延均衡补偿网络设计，在应用时还需考虑元件外部控制电路的复杂程度、元件一致性、MEMS可动结构可靠性等问题。

[1] 焦义文，王元钦，马宏，等.群时延失真对天线组阵合成信噪比的影响分析[J].信号处理，2015，31(2)：145-151.

[2] 张金贵.信道特性对卫星通信系统性能影响仿真[J].无线电工程，2015，45(4)：9-11.

[3] ALOMAR W，MORTAZAWI A.Elimination of Beam Squint in Serially Fed Arrays with Negative Group Delay Circuits Incorporating Antenna Elements[C]∥Proceedings of the 42nd European Microwave Conference，2012：625-627.

[4] 邓良.负群时延微波电路的研究与设计[D].南京：南京理工大学，2015：1-74.

[5] RAVELO B，PERENNEC A，ROY M.Broadband Balun Using Active Negative Group Delay Circuit[C]∥Proceedings of the 37th European Microwave Conference，2007：466-469.

[6] 杨林川，李茂辉，张德伟，等.一种Ku波段群时延均衡器的设计[J].信息工程大学学报，2014，15(5)：576-579.

[7] 陈叔远，颜绍书.相移均衡器[M].北京：人民邮电出版社，1984：5-80．

[8] 江涛.变频链路群时延特性研究[J].现代雷达，2008，30(5)：112-115．

[9] 侯利明，孙宝升，陆晓明.群时延特性对卫星高速数传中继系统的影响[J].飞行器测控学报，2006，25(2)：54-58．

[10] RICHARD L.A Handbook Formula for the Inductance of a Single-layer Circular Coil[J].Proc.IEEE，1985，73(9)：1428-1429.

[11] BURGHARTZ J N，REJAEI B.On the Design of RF Spiral Inductors on Silicon[J].IEEE Trans.on Electron Devices，2003,50(3)：718-729.

[12] PIERNAS B，NISHIKAWA K，KAMOGAWA K，et al.High Q-Factor Three-Dimensional Inductors[J].IEEE Trans.on Microwave Theory Tech.，2002，50(8)：1942-1949.

[13] WU H C,TZUANG C K C.PBG-Enhanced Inductor[C]∥IEEE MTT-S Int.Microwave Symp.Dig.，2002：1087-1090.

[14] PIETERS P，VAESEN K，BREBELS S，et al.Accurate Modeling of High-Q-Spiral Inductors in Thin-Film Multilayer Technology for Wireless Telecommunication Applications[J].IEEE Trans.Microwave Theory Tech.，2001，49(4)：589-599.

[15] SUTONO A，HEO D.High-QLTCC-based Passive Library for Wireless System-on-Package Module Development[J].IEEE Trans.on Microwave Theory and Tech.，2001,49(10)：1715-1724.

[16] 孟真，刘燕春，赵文英，等.采用磁性基板的高感值PCB平面电感器设计[J].电子与封装，2015，15(1)：14-18.