有序化砂轮磨削表面粗糙度仿真

赵国伟，吕玉山，李雨菲，李伟凡

（沈阳理工大学 机械工程学院，辽宁 沈阳 110159）

1 引言

随着科学技术的发展，磨削技术已经成为精密加工技术领域的重要支撑技术。但是传统的砂轮表面的磨粒排布是无序的，这使得在磨削过程中很容易造成砂轮表面阻塞，使得工件的表面质量下降，砂轮的寿命降低，而且磨料的利用率也相对较低。因此在砂轮制造工艺过程中，保证磨粒的有序化排布是提高砂轮磨削性能的关键技术[1]。为了提高超硬磨料砂轮的磨削性能，很多学者已经对砂轮表面的磨粒有序化排布进行过探讨，并取得了一些非常重要的成果。文献[2]对磨粒规则几何分布砂轮进行了仿真优化，基于此设计制造出了最佳有序排布磨粒的电镀砂轮结构，实验证明该砂轮的磨削工件表面得到改善。文献[3]在利用金刚石有序排列技术制造出的单层钎焊金刚石磨轮进行精密磨削加工时，得到的加工工件表面粗糙度明显降低。文献[4]对有序排布磨粒砂轮的磨料分布高度和分布间距等对表面粗糙度的影响规律进行了研究，结果表明：经过磨粒的错位排布，可以适当降低磨削表面粗糙度值。文献[5-6]在2010年CIRP中关于超精密磨削的年度报告中指出，使用有序排布磨粒的砂轮能够实现超精密磨削。文献[7]进行了磨料优化排布磨盘实验，结果表明磨料优化排布能够改善磨具的磨削性能。在相同磨粒密度下通过对叶序、错位和无序排布磨粒砂轮的磨粒运动轨迹建模，将所有参与切削的磨粒运动轨迹通过合理算法叠加生成工件表面形貌，然后仿真了不同排布磨粒砂轮在缓进给过程中的工件表面粗糙度。

2 磨粒有序化排布砂轮设计

根据文献[8]提出的柱面叶序排布理论，得出磨料叶序排布砂轮上任一磨粒的柱面坐标公式：

式中：n—种子在圆柱表面上的序数，从圆柱的底部算起；φ，R，H—圆柱坐标（第n个种子的）；α—叶序发散角，为137.508°；h—叶序生长系数，控制着磨粒之间的间隙。

错位排布与叶序排布具有相同的磨粒密度，在相同直径ds下，由相同的磨粒数N可推得错位排布砂轮中，磨粒之间的间距K为：

式中：k=0.5，由磨粒间距K可得出砂轮周向磨粒行数b和轴向磨

粒行数j分别为：

则在磨削过程中，磨粒错位排布砂轮上任一磨粒的圆柱坐标公式为：

对于磨粒无序排布砂轮，指磨粒随机分散在砂轮圆柱表面，并没有确定的间距，在磨削过程中，无序排布磨粒点的圆柱坐标公式为：

式中：random—随机函数。

一些文献[9]表明磨粒矩阵排布砂轮的磨削性能较差，砂轮表面粗糙度较大，因此，不进行讨论和仿真分析。基于上面的磨粒排布理论，砂轮表面的磨粒排布就可以依据以上方程式子来设计。利用三维软件设计的砂轮图，如图1所示。可明显看出相同磨粒密度下不同排布方式的砂轮表面对比情况，其中叶序排布磨粒可使相邻四个磨粒实现错位互补。

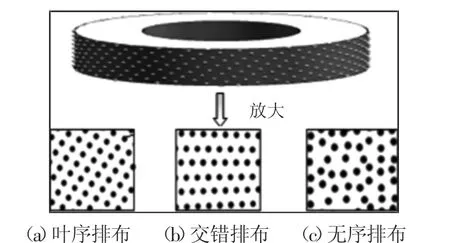
图1 磨粒不同排布砂轮的整体与局部图Fig.1 The Whole and Partial Amplification Figure of Grinding Wheel With Different Patterns

3 仿真模型的建立

3.1 磨粒运动轨迹

在磨削运动过程中，砂轮上的磨粒对于砂轮做高速旋转运动，相对于工件不停做进给运动。磨粒运动几何模型，如图2所示。以磨粒最低点 o’为原点，建立坐标系 o’xyz，o点为砂轮中心，ds为砂轮直径，vs、vw、aP分别为砂轮线速度、工件进给速度和磨削厚度，θ为砂轮在单位时间内转过的角度，ω为砂轮角速度，y为沿砂轮轴向分布的磨粒位置。假设磨粒切削刃在最低点o’和工件开始接触，磨粒向上运动，则在任意时刻t，磨粒的运动轨迹，如图2所示。磨粒在磨削工件时，后进入切削区的砂轮磨粒要切削先前磨粒切削表面，因此需要对相邻磨粒进行讨论，2颗相邻磨粒磨削轨迹示意图，如图3所示。

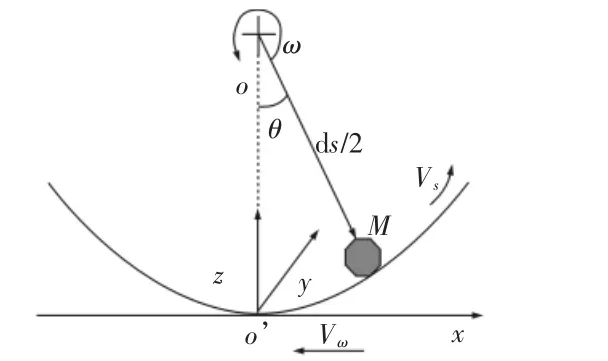
图2 单颗磨粒运动示意图Fig.2 Schematic Diagram of a Single Grain Motion Trail

图3 相邻2颗磨粒磨削轨迹示意图Fig.3 Schematic Diagram of Two Adjacent Grain Motion Trail

建立第一颗磨粒M1局部坐标系o1’，并且使得该局部坐标系与总体坐标系o重合。同样建立第二颗磨粒M2的局部坐标系o2’，并将磨粒M2在局部坐标系o2’下的运动轨迹经过平移变换转换到全局坐标系o’下，首先确定其横向距离Δs，再确定其纵向距离Δr，最终推倒出第i颗磨粒ni的运动轨迹方程。针对叶序、交错、无序三种不同的砂轮排布方式，分别对砂轮表面任意一颗磨粒的运动轨迹进行分析与推倒。两个坐标系之间的径向距离Δr，由图4可以看出，即为磨粒M1与磨粒M2的半径之差，推广到第i颗磨粒，则可以表示为：

砂轮由第一颗磨粒运动到第二颗磨粒，在工件表面形成划痕，划痕之间的间距Δs均可以表示为：

式中：K—磨粒之间间距，在叶序排布砂轮中k=1，在交错排布砂轮中k=0.5。

结合图3所示相邻两磨粒之间的运动关系，依据单颗磨粒的运动轨迹方程，将以上横向和纵向距离带入推倒，可得出叶序、交错和无序排布下砂轮表面第i磨粒的运动轨迹方程：

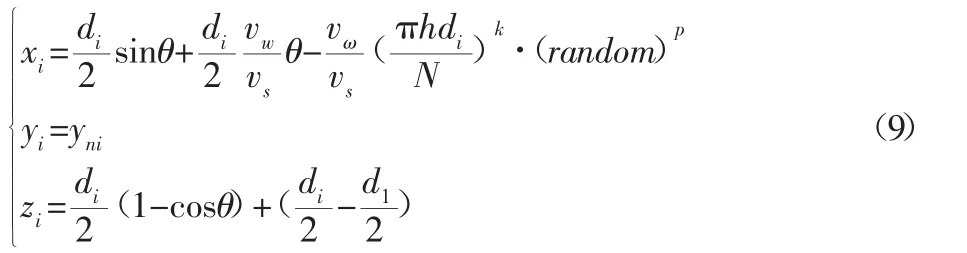
式中：h—叶序生长系数；dS—砂轮直径；N—磨粒在砂轮基体表面穿过的磨粒数；k，p—系数，在叶序排布中k取1，p取0，在错位排布中k取0.5，p取0，在无序排布中k取1，p取1。random—随机数，j—沿砂轮轴向位置分布的行数；di—砂轮中心至磨粒顶点的距离，可表示为：

式中：hi—不同磨粒在砂轮表面的的切刃突出高度。

3.2 磨粒切削刃突出高度

磨削工件表面粗糙度不仅与砂轮单位面积磨粒数、磨粒分布及切削痕迹有关，而且与磨粒在砂轮表面的切削刃突出高度分布更存在直接关系。研究表明，磨粒的切削刃裸露高度服从正态分布[10]，其概率密度分布函数 h（i）：

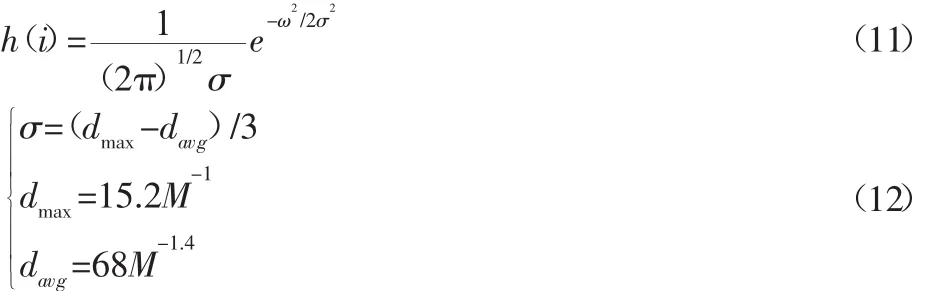
式中：M—磨粒的粒度；dmax、davg—磨粒的最大直径和平均直径。将h（i）带入上述磨粒的运动轨迹方程，可得出磨粒的切削深度。

3.3 工件表面形貌生成过程

磨削工件表面是由外圆砂轮表面上所有磨粒共同切削后生成的，是由所有参与切削的磨粒运动轨迹叠加而成。由于外圆砂轮表面磨粒高低不等，排布不同，疏密不均，磨粒的切削运动轨迹不断发生变化，最终在砂轮一次次切削工件后留下高低起伏的痕迹，形成工件表面粗糙度曲线，通过叠加沿砂轮径向和轴向分布的磨粒运动轨迹，提取残留在工件表面的最低轨迹线，最终生成工件的三维表面形貌。

4 磨削工件表面仿真

4.1 磨削工件工件表面仿真设计流程

为提高运算速度，采用球型磨粒进行仿真，设定其突出高度和分布状态，然后设置仿真区域，输入砂轮几何参数和磨削参数，利用循环语句对所有参与切削的磨粒运动轨迹进行迭代，最后提取留在工件表面的最低切削曲线，即得到磨削工件表面三维形貌。

4.2 磨削工件表面仿真结果与分析

在仿真过程中，设置砂轮直径ds=100 mm，砂轮宽度H=10mm，磨粒粒度为 45#～50#，叶序系数 h=0．0016，砂轮表面总磨粒数6250个，砂轮与工件轴线的变量角度α为0°。图4（a）～图4（c）分别是叶序、错位、无序排布砂轮在砂轮速度vs=50 m/s，工件速度vw=50mm/min，切削厚度ap=0．4mm时，生成的最具代表性的工件三维形貌。从图4中可以明显看出，在相同的磨削条件下，叶序排布外圆砂轮磨削工件表面留下的圆弧形磨粒切削痕迹趋于平稳，仿真表面趋于光滑。错位排布和无序排布砂轮磨削的工件表面沟槽间距不匀，有明显的切削痕迹，尤其是无序排布，沟痕最深，表面形貌最差。在磨削过程中，砂轮速度vS，工件速度vw，切削厚度ap都对工件表面粗糙度产生一定的影响，取叶序系数h=0．0016，对不同磨粒排布方式下砂轮磨削进行模拟仿真。取工件速度vw=50mm/min，切削深度ap=0．4mm，不断改变砂轮的磨削速度，砂轮磨削的工件表面粗糙度变化趋势，如图5所示。从图5中可看出，适当提高砂轮的转速有助于改善砂轮磨削工件的表面质量，各种砂轮磨削的工件的表面粗糙度在vs=50m/s时比vs=20m/s时有所改善，叶序砂轮表面粗糙度由最初的2．0μm降低至0．88μm，叶序砂轮与其他排布的砂轮在相同的砂轮速度下，得到的工件表面粗糙度值最小，其次是错位排布，无序排布最大。随着砂轮速度的提高，单位时间内参与切削的有效动态切削刃增多，因此，得到的表面粗糙度较低。

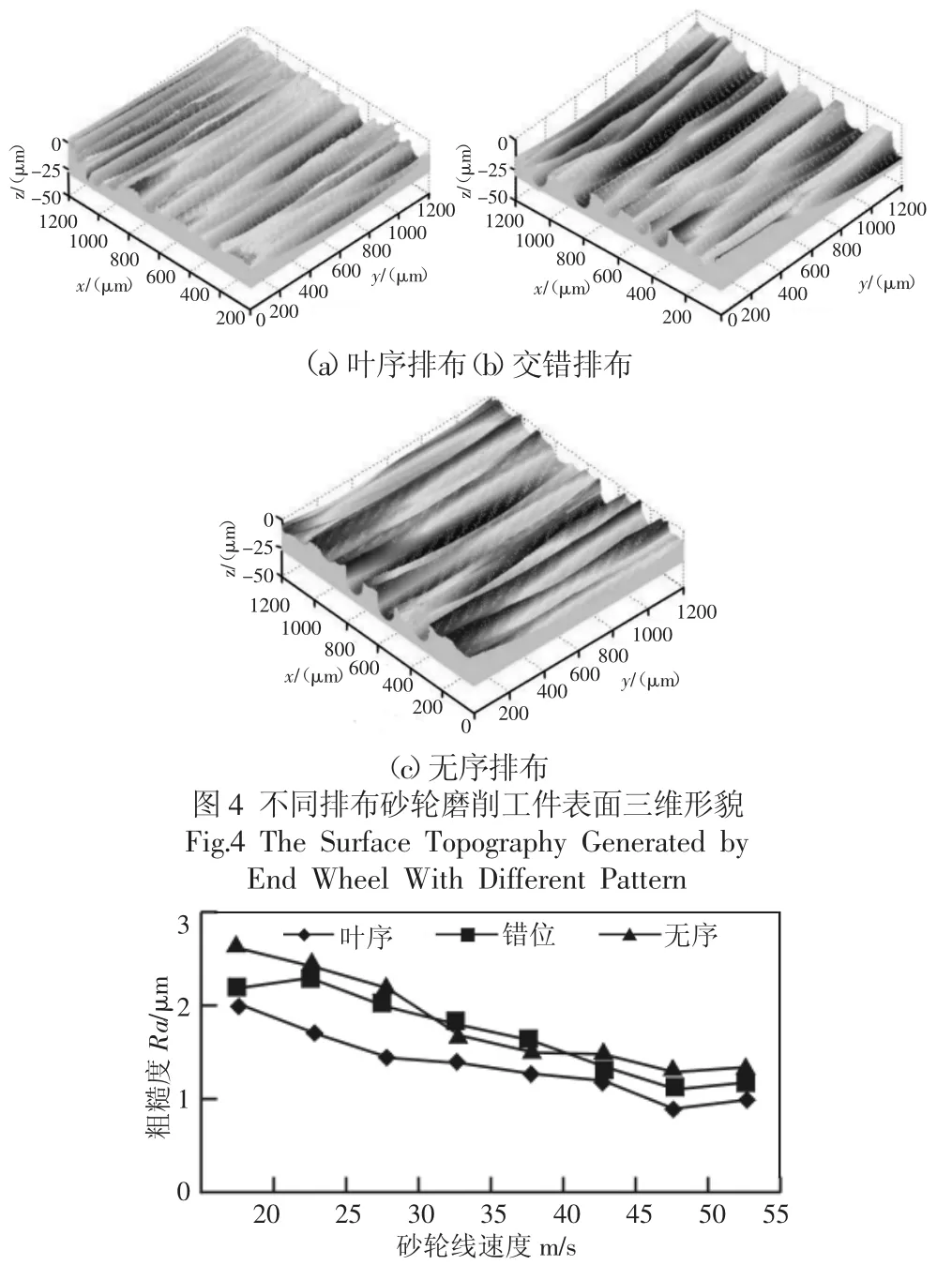
图5 砂轮速度的变化对磨削工件表面粗糙度的影响Fig．5 The Effects of Grinding Wheel Speed on the Surface Roughness

取磨削深度ap=0．4mm，砂轮速度vs=45m/s时，不断改变工件进给速度，砂轮磨削的工件表面粗糙度变化趋势，如图6所示。从图6中可以看出，在保证砂轮速度和切削深度不变的情况下，随着工件进给速度的增加，工件表面粗糙度呈上升趋势。由于叶序排布砂轮磨粒达到最大饱和状态，在单位时间内参与切削的动态有效磨粒数比错位和无序的多，其获得的工件表面粗糙度最低。在工件进给速度为80mm/min时，由仿真数值计算得到的叶序排布工件表面粗糙度为 0．9μm，错位为 1．12μm，无序为 1．43μm。当工件进给速度 vw=50mm/min，砂轮速度vs=45m/s，不断变换磨削深度，砂轮磨削的工件表面粗糙度变化趋势如图7所示。由图7可看出，当磨削深度为0．4mm时，不同磨粒排布下工件表面粗糙度较小，叶序砂轮得到的粗糙度值最小为1．05μm。磨削深度越大，磨粒切削切痕越深，磨粒之间的干涉越率越低，得到的工件表面粗糙度越大。当磨削深度为3．2mm时，叶序、错位、无序排布得到的表面粗糙度分别为2．8μm、3．2μm、3．43μm。在不同的磨削深度下，叶序排布砂轮得到的工件表面粗糙度值低于其他排布方式的砂轮。

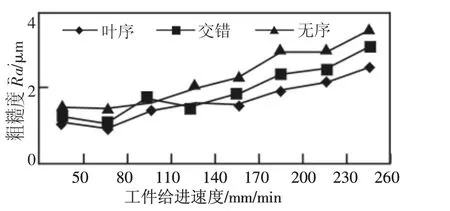
图6 工件速度的变化对磨削工件表面粗糙度的影响Fig．6 The Effect of Workpiece Feeding Speed on the Surface Roughness

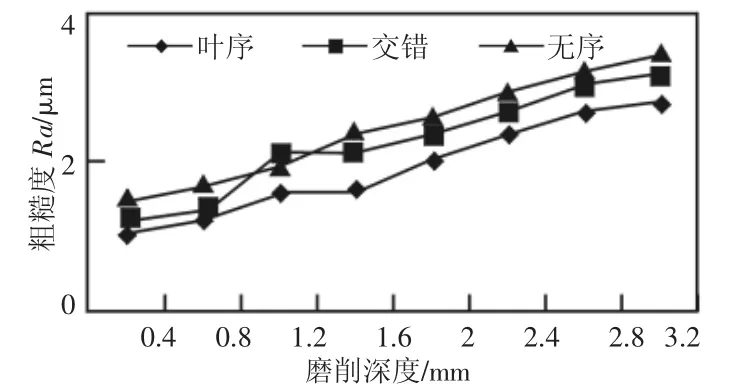
图7 切削深度的变化对磨削工件表面粗糙度的影响Fig.7 The Effects of Grinding Depth on the Surface Roughness

5 结论

根据磨粒运动轨迹，建立了叶序、错位、无序三种不同磨粒排布下的仿真模型，生成了工件表面三维形貌。在相同的磨削参数下，叶序排布砂轮相比错位和无序砂轮，得到的磨削工件表面较光滑，工件表面粗糙度值较低，磨削性能较好。在缓进给磨削过程中，随着砂轮速度的增大，工件进给速度的减小，磨削深度的减小，磨削工件表面粗糙度值皆变小。

［1］王涛，李剑，高航.磨削技术的现状与发展趋势［J］.机械设计与制造，2003.（Wang Tao，Li Jian，Gao Hang.Status and progress of grinding technology［J］.Joumal of Mechanical Design and Manufacturing，2003.）

［2］Aurich J C，Herzenstiel P，Sudermann H.High-performance dry grinding using a grinding wheel with a defined grain pattern［J］.CIRP Annals-Manufacturing Technology，2008.

［3］T.0hi Trends and future development for diamond CMP pad conditioners［J］.IDR，2004.

［4］Koshy P，Iwasaki A，Elbestawi M.Surface generation with engineered diamond wheels：insights from simulation［C］.Annals of the CIRP，2003.

［5］BrinksmeierE.，MutlugunesY.，KlockeF.Ultra-precisiongrinding［J］.Annals of The CIRP，2010.

［6］Ahearne E.，Byrne G..Simulation of the local kinematics in rotational grinding［J］.Annals of The CIRP，2008.

［7］Butler-Smith P.W.，Axinte D.A.Daine M.Ordered diamond micro-arrays for ultra-precision grinding—An evaluation in Ti-6Al-4V，International［J］.Journal of Machine Tools&Manufacture，2011.

［8］Van Iterson G.Mathematische und mikroskopish-anatomische Studien iiuber Blattstellungen［J］.Gustav Fischer，Jena，1907.

［9］周生合.叶序排布CBN电镀砂轮磨削的表面粗糙度研究［D］.沈阳：沈阳理工大学，2014.（Zhou Sheng-he.Research on the grinding surface roughness of the electroplated CBN wheel with phyllotactic pattern［D］.Shenyang：Shenyang Ligong University，2014.）

［10］Zhong De-shi.Grinding with electroplated Cubic Boron Nitride（CBN）wheels［D］.Dissertation of Doctor the University of Massachusetts Amherst，2004.