两片变刚度全啮合钢板弹簧粒子群优化设计
2018-03-21游雄杰干年妃
游雄杰,干年妃,程 超
(湖南大学 汽车车身先进设计制造国家重点实验室,湖南 长沙 410082)
1 引言
少片钢板弹簧作为汽车悬架的弹性元件在重量上有很大的优势,能够有效的降低整车自重。同时它的材料利用率高,能够节约原材料,降低成本。而少片变刚度钢板弹簧不仅能够实现轻量化,还能显著提高整车的舒适性能。少片变刚度钢板弹簧己经成为重型载货汽车的发展趋势[1]。
目前,少片变刚度钢板弹簧广泛应用于轻、微型汽车的悬架系统。主副簧接触型式主要是抛物线型或渐开线型,对于少片变刚度钢板弹簧的优化设计与计算中的应力计算一般采用经验公式修正[2],对整个接触过程的板簧应力变化研究较少。主要是使用优化工具箱或其它优化算法,对板簧进行单目标轻量化的优化设计[3]。单目标轻量化的优化算法虽然对应力和刚度有约束,但仍具有很大的盲目性和随机性,有时甚至会优化不出结果,得不到满意的结论,导致做到轻量化的同时,悬架的可靠性能和平顺性能又难以达到要求。
在原有设计理论的基础上[4-6],采用全啮合曲线型的接触型式,提出一种新的少片变刚度板簧的设计计算方法。以某重卡牵引车少片变刚度全啮合钢板弹簧为例,进行试验设计,建立三个目标之间的二次多项式函数近似模型,将多目标优化算法引入到板簧优化设计过程中,找到几个目标和变量之间的变化关系,从而得到一个非劣解集,根据设计需求从解集中选取期望的设计参数,以克服单个目标优化的盲目性。最终对少片变刚度全啮合板簧进行优化设计,取得了良好的效果。
2 建立两片变刚度全啮合主副簧数学模型
由于钢板弹簧左右对称,故可取其一半进行分析。对于梯形变截面板簧,其设计参数包括:半主簧长度lm;主簧板端长度x(1);主簧根部长度lm2;主簧板端厚度x(2);主簧根部厚度x(3);半副簧长度 x(4);副簧根部长度 la2;副簧板端厚度 x(5);副簧根部厚度x(6)。主副簧共同作用时板簧二分之一模型,如图1所示。

图1 主副簧共同作用时板簧二分之一模型Fig.1 One Half of Leaf Spring Model When Main Spring and Auxiliary Spring Acting Together
当主副簧开始共同起作用,即从开始接触,直到完全接触,主副簧质量与空载偏频不随接触过程变化。单片板簧的质量与刚度空载偏频计算[7],此处不再赘述,全啮合过程主副簧最大工作应力的计算方法推导如下。
当主副簧接触位置距离主簧端部为x,此时加载在主簧端部的载荷为:

式中:p1—主副簧刚要开始接触时加载在主簧端部载荷p的取值;p2—主副簧刚好完全接触时加载在主簧端部载荷p的取值。
接触过程中主副簧最大工作应力按以下两种情形计算:
第一种情形:当 x(1)≤lm-x(4)时;
当 0≤x≤x(1),hz=(2);

第二种情形:当 x(1)≥lm-x(4)时;
当 0≤x≤lm-x(4),hz=x(2);

当 lm-x(4)≤x≤x(1),hz=x(2),变截面区间 hf与 x 呈线性变化;

式中:pw—满载时主簧端部载荷;wz—主簧各截面断面系数;Iz—主簧各截面惯性矩;wf—副簧各截面断面系数;If—副簧各截面惯性矩;σmax_z—主簧最大工作应力;σmax_f—副簧最大工作应力。
主副簧的最大工作应力可按下式计算:

3 两片变刚度全啮合主副簧多目标优化试验设计
以该牵引车两片变刚度全啮合钢板弹簧的多目标优化设计为例来验证结果是否可靠。该牵引车的前桥钢板弹簧已经做到两片变截面定刚度钢板弹簧,原质量为37kg。具体设计参数如下:lm=765mm,lm2=la2=115mm,B=90mm。按超载设计,空载轴荷:19000N;满载轴荷:47400N。板簧材料为51CrV4,抗拉强度达到1350MPa以上。
一般来说,板簧质量越轻,满载刚度越小,满载偏频越小,这两者不相矛盾,不用寻求平衡解。而理想的板簧设计参数是在做到轻量化的同时可靠性能和平顺性能都较优,因此利用多目标算法对板簧质量、最大工作应力以及空载偏频进行优化,以寻求三个目标之间的平衡解,找到满足理想性能的板簧设计参数。板簧的多目标优化问题可以用公式表示:

式中:fm—钢板弹簧质量;
σmax—主副簧最大工作应力;
fz—空载偏频。
而在影响质量、应力和空载偏频的诸多因素中,对板长和板厚的优化是最为可行的,因此选取板簧主簧板端长度x(1);主簧板端厚度 x(2);主簧根部厚度 x(3);半副簧长度 x(4);副簧板端厚度 x(5);副簧根部厚度 x(6)作为此次优化的设计变量[8]。上述的取值范围是根据板簧设计规格和加工要求确定的。各变量的优化区间,如表1所示。

表1 设计变量的优化区间Tab.1 Design Variable Bounds
其具体优化流程,如图2所示。
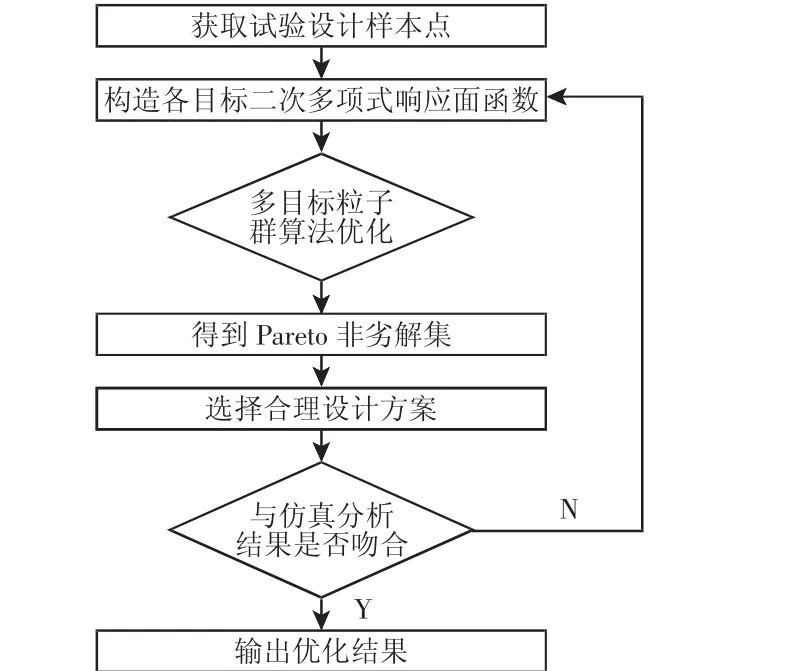
图2 板簧多目标优化流程图Fig.2 Flow Chart of Leaf Spring Multi-Objective Optimization
3.1 试验设计方法
基于回归分析的近似模型方法是针对样本数据进行操作的,因此样本点选取的优劣决定了所构建的近似模型的正确性。为建立精度和效率都较高的近似模型,需要选取合适的样本点,如果样本选择不当则有可能造成近似模型精度较低,甚至错误等结果。采用拉丁超立方试验设计方法,该方法的基本思想是将每个设计参数的设计空间均匀地划分为边长为N的方阵,然后在方阵中随机取得不同行不同列的N个采样点。此方法的采样点比较均匀,可获得充分的模型信息。
采用拉丁超立方试验设计方法,获取100组样本点。即得到100组板簧长度厚度参数,由于篇幅原因仅列出一些样本,数据所列,如表2所示。

表2 板簧参数样本点Tab.2 Parameters of Leaf Spring Sample Points
根据100组样本点,分别建立100组板簧的数学模型,计算出各自的质量,并得到每组的最大工作应力值和空载偏频。
3.2 二次多项式响应面模型
近似模型的基本思想是,通过数理统计和试验设计的方法,在设计变量和相应值之间建立一种现实的函数关系来近似复杂的实际问题或函数。常用的近似模型方法有Kriging响应面法、径向基函数法、多项式响应面法及移动最小二乘法等。
求解复杂问题时通常需要更高阶次的多项式函数来提高拟合精度,此时响应面模型的回归系数也会随之大幅增加,尤其对于多变量的问题,其计算量很大且计算时间长,难以满足工程需求。研究表明,二阶多项式响应面模型基本能满足绝大多数工程问题的求解,有较好的计算精度和求解效率,因此,采用二次多项式响应面模型来构造目标与变量之间的函数关系,其对目标估计的基本形式可以表示为[9]:
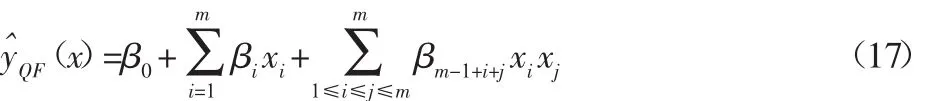
式中:x∈Rm—设计变量;m—x 的维数;β0、βi、βm-1+i+j—常数项系数、一次项系数、二次项系数。
由样本点得到二次多项式近似模型的关键是求解系数矩阵β,该矩阵可通过最小二乘法求得:

质量fm本身就是关于x的二次多项式响应面函数,其系数矩阵β1为:
β1=[0,0,0.4592,0.6217,0,-0.0812,0.0812,0,0,0,0,0,0,0.0007,
-0.0007,0,0,0,0,0,0,0,0,0,0,0.0007,0.0007,0]。
对于应力的二次多项式响应面函数σmax的系数矩阵,系数矩阵β2取如下值时,二阶多项式响应面模型与采样点拟合最好。

对于空载偏频的二次多项式响应面函数fk的系数矩阵,系数矩阵β3取如下值时,二阶多项式响应面模型与采样点拟合最好。

3.3 基于粒子群算法的优化设计
粒子群优化算法源于对鸟类群体觅食行为的研究,有学者观察到鸟类在寻觅食物的时候会经常变换寻找方向,并且有时聚拢、有时分散,飞行轨迹难以猜测,但是全体鸟群却总是能够持续同步,鸟群中每个个体之间同样能够维持适当的距离,学者们对这种生物种群进行了深入的研究,他们发现在种群活动时群体内会进行信息传递与沟通,这就为种群的共同进化创造了条件,这便是PSO优化算法形成的基础。该种理论的核心便是个体间的沟通和交流,这是在全局范围内寻找最优解的基础,通过群体中每个个体之间的相互协作和信息交流来寻求问题的全局最优解。
对于多数的多目标寻优问题,其各目标往往不可比较,有时甚至会互相冲突,提升一个目标的性能往往会导致其它目标性能的下降,因此,此类问题无法找到确定的最优解来同时满足所有目标,但我们能够寻求满足如下条件的解:其中的某个或者多个目标无法获得更优值,而其余所有目标的性能也不会恶化,我们通常利用这种Pareto非劣解集来指导工程中的优化设计[10-12]。利用多目标粒子群算法对钢板弹簧三个目标函数寻找平衡解,设置粒子群算法控制参数:取惯性权值w=0.7,加速因子c1=c2=1.5,种群规模nPop=100,存储大小nRep=100,最大迭代次数MaxIt=100,经过100代优化计算,得到满足设计要求的Pareto非劣解集。根据设计需求从Pareto解集中选取期望的设计参数,最后选取的一组优化目标值:质量为31kg,最大工作应力为629.7MPa,空载偏频为3.173Hz。对应板簧设计参数为 X=[149.5,14.1,24.7,498.4,9.1,19.2]。
3.4 优化结果分析
将优化后的板簧设计参数代入到数学模型中计算得到空载偏频为2.998Hz,满载偏频为1.865Hz,质量为31kg,最大工作应力为654.6MPa。在MATLAB中画出最大工作应力,如图3所示。
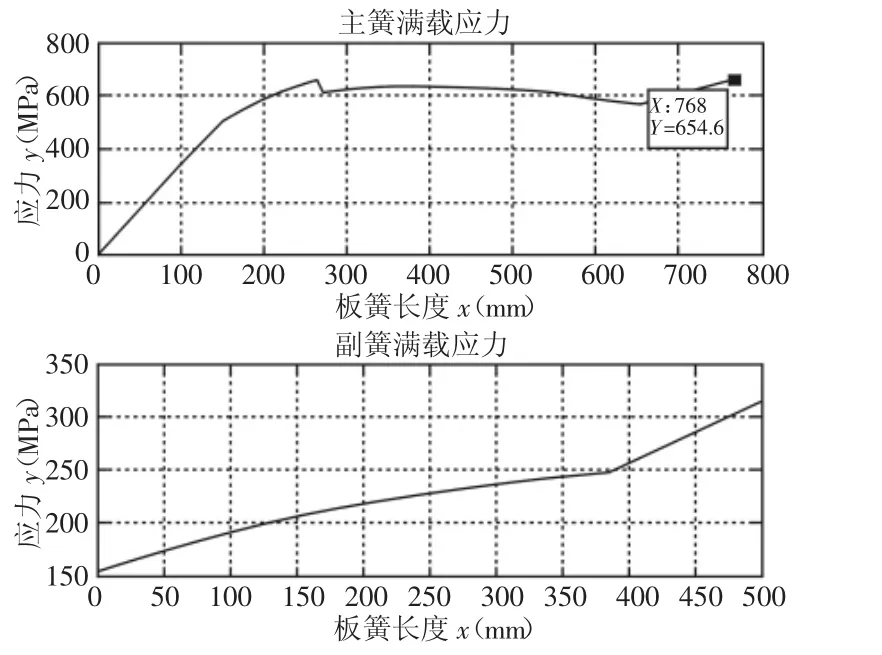
图3 MATLAB工作应力图Fig.3 Stress Drawing in MATLAB
利用优化后得到的板簧设计参数拟合出板簧自由状态曲线,在三维软件中建模,通过专业的有限元前处理软件Hypermesh和ANSYS后处理功能,得到新的结构应力云图,如图4所示。结果显示板簧的最大工作应力为644.4MPa。对比近似模型的优化结果和图3、图4可以看出:优化后利用理论数学模型与有限元模型都验证了结果的可靠性。其最大工作应力值(均在650MPa左右)远低于其材料的抗拉强度1350MPa,安全系数为2.1,可以满足材料应力要求。由多目标粒子群算法优化所得的板簧性能参数与优化前的设计对比,如表3所示。

图4 ANSYS工作应力云图Fig.4 Stress Drawing in ANSYS

表3 优化前后悬架性能对比Tab.3 The Performance of Suspension Before and After Optimization
4 结论
针对某牵引车钢板弹簧的优化问题,建立该车型的两片变刚度全啮合钢板弹簧数学模型,对钢板弹簧质量、最大工作应力和空载偏频进行多目标粒子群优化设计,再通过仿真和有限元分析验证了结果的可靠性。变刚度全啮合钢板弹簧保证了主副簧每一点都充分接触,由图4可知,板簧材料的利用率非常高,大部分区域应力都按等强度分布。两种仿真应力预测结果相对误差在5%以下。由表3可知,在保证可靠性的前提下,空满载偏频分别从3.5Hz和1.91Hz降到了2.998Hz和1.865Hz,空满载平顺性能得到了较大改善,同时,板簧质量在少片簧的基础上由37kg减少到了31kg,又减轻了16.2%,实现了轻量化。
[1]马文伦.重型载货车少片变截面钢板弹簧的研究[D].哈尔滨:哈尔滨工程大学,2009(3):1-18.(Ma Wen-lun.Research of a heavy duty truck taper-leaf spring[D].Harbin:Harbin Engineering University,2009(3):1-18.)
[2]韦进光,李宏典,麦承贤.渐变刚度板簧(单片副簧)的经验算法[J].装备制造技术,2009(5):63-68.(Wei Jin-guang,Li Hong-dian,Mai Cheng-xian.Experiential calculation for leaf spring with single auxiliary leaf andy way[J].Equipment Manufacturing Technology,2009(5):63-68.)
[3]郑银环,张仲甫.少片渐变刚度钢板弹簧的优化设计与计算[J].机床与液压,2005(3):44-48.(Zheng Yin-huan,Zhang Zhong-fu.Optimum design and calculation of variable rate leaf spring[J].Machine Tool and Hydraulics,2005(3):44-48.)
[4]唐应时,付建朝,姚汉波.两片变截面变刚度钢板弹簧遗传优化设计[J].湖南大学学报:自然科学版,2011(10):39-43.(Tang Ying-shi,Fu Jian-chao,Yao Han-bo.Optimal design of taper leaf spring with variable stiffness based on genetic algorithms[J].Journal of Hu’nan University,2011(10):39-43.)
[5]陈凯.某平衡悬架少片变截面钢板弹簧结构分析与关键技术研究[D].长沙:湖南大学,2013(3):8-28.(Chen Kai.The structural analysis and the key technology research of a balanced suspension taper-leaf spring[D].Changsha:Hunan University,2013(3):8-28.)
[6]王霄锋.汽车底盘设计[M].北京:清华大学出版社,2010:282-297.(Wang Xiao-feng.Automotive chassis design[M].Beijng:Tsinghua University Press,2010:282-297.)
[7]王望予.汽车设计[M].北京:机械工业出版社,2007:181-190.(Wang Wang-yu.Automotive design[M].Beijing:China Machine Press,2007:181-190.)
[8]I.Rajendran,S.Vijayarangan.Optimaldesignofacomposite leaf spring using genetic algorithms[J].Computers&Structures,2001(4):1121-1129.
[9]张勇.基于近似模型的汽车轻量化优化设计方法[D].长沙:湖南大学,2008(12):13-17.(Zhang Yong.A method of vehicle lightweight optimization design basing on the approximate model[D].Changsha:Hu’nan University,2008(12):13-17.)
[10]Q M Fan.Multi-objective optimization design for gradient stiffness leaf spring[J].Fourth International Conference on Information&Computing,2011:354-357.
[11]纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社,2009:21-50.(Ji Zhen,Liao Hui-lian,Wu Qing-hua.Particle swarm optimization(pso)algorithm and application[M].Beijing:Science Press,2009:21-50.)
[12]Cocllo C A C,Pnlido GT,Lechnga M S.Handling multiple objectives with particle swarm optimization[J].IEEE Transactions on Evolutionary Computation,2004:256-279.
