滚齿机刀架传动系统刚度对其性能的影响研究

赵江坤，王时龙，胡宗延

（重庆大学 机械传动国家重点实验室，重庆 400044）

1 引言

齿轮是装备制造业中极为重要的基础件，精密超精密齿轮加工是机械制造业的发展方向，高精度齿轮机床是实现精密齿轮加工的首要条件。齿轮机床的精密传动系统的性能直接决定机床的加工精度和性能，而机床精密传动系统的性能受到了诸多因素的影响，比如接触部件间间隙，传动链的刚度以及机电系统参数多元耦合等[1-4]。现代精密机床大都采用位置环反馈来保证精度，位置闭环控制对刚度非常敏感。保证传动系统刚度才能避免其发生电子学振荡。而且系统伺服刚度是影响系统加工精度的重要因素。国内外学者在该领域做了大量的研究工作，文献[5]通过建立考虑传动链刚度和间隙的二自由度数学模型并基于机床进给系统的传动函数模型，分析了其对系统输出的影响。文献[6-7]建立了直驱进给伺服系统的刚度模型，分析了系统伺服参数对跟随误差和进给系统稳定性的影响。文献[8]利用闭环传递函数的灵敏度研究了数控机床传动刚度的变化对运动精度稳定性的影响。文献[9]建立了某传动链刚度模型，得到了传动链每个元件对整体刚度的影响因子，研究了传动链刚度对其输出行为的影响。但是文中用工艺系统刚度的方法来等效传动链刚度，忽略了啮合刚度的影响。另外中外文献中鲜有提及控制系统参数与机械参数之间的耦合关系。不匹配的控制参数容易导致系统出现振荡、超调、运行不稳定等问题，直接影响到设备的稳定性和效率[10]。

从全局机电耦合分析的角度，建立了某型滚齿机刀架传动系统机电耦合模型。然后基于静刚度定义，建立计及齿轮副啮合刚度、传动轴扭转刚度的动力学模型，获取刀架传动链的机械刚度模型。深入研究了机械刚度、系统伺服刚度、系统跟踪误差以及控制器参数之间的匹配关系，揭示了机械刚度和系统伺服刚度对刀架传动系统性能的影响规律。

2 刀架传动系统建模

2.1 传动系统机电耦合模型的建立

某型滚齿机刀架传动系统的机构简图，如图1所示。采用电机经三级齿轮减速驱动滚刀轴旋转。第一级为直齿轮传动，后两级为斜齿轮传动。该系统是内环为速度环，外环为位置环的双闭环控制系统。可针对每一模块的物理特性（机理建模方法）单独建立其数学模型。分析每一模块间的相互耦联关系，根据它们的耦联参数便可建立传动系统全局机电耦合模型。

图1 刀架传动系统机构简图Fig．1 Schematic Diagram of Tool Carrier Transmission System

2.1.1 伺服电机

输入为电枢电压Ud，输出为电动机转角。根据牛顿第二定律，基尔霍夫电路定律可得到以下方程式：

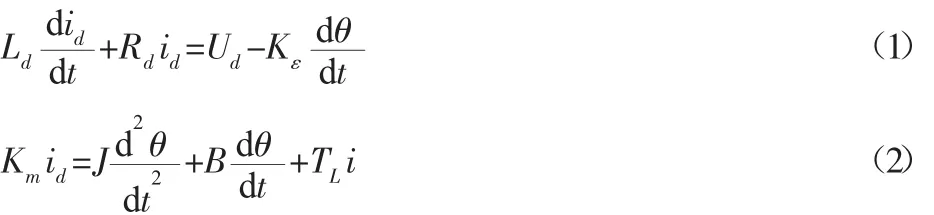
式中：Ld、id—电枢电感、电枢电流；Rd—电枢电阻；TLi—等效负载转矩；Km、Kε—电矩系数和反电势系数；J、B—电机转动惯量和阻尼系数。

2.1 .2机械传动装置

刀架传动系统的机械装置为三级齿轮减速机构，输入为电机转角θ，输出为滚刀轴转角θL。可得方程式：

式中：K—传动系统机械刚度；JL、BL—传动系统转动惯量和阻尼系数。

根据输入偏差信号可将式（1）电流方程变形为：

将式（2）～式（4）进行拉布拉斯变换，联立可得系统的机电耦合控制方框图，如图2所示。

图2 系统传递函数结构框图Fig．2 Block Diagram of System Transfer Function

2.2 机械刚度建模

在齿轮传动过程中，即使加工制造、装配没有误差。也会因为齿轮副，转轴的弹性变形而使输出转角产生一定的偏差，这个偏差值即为静传递误差。在不考虑机械系统加工制造、装配误差时，刀架传动系统的机械刚度即为负载转矩和传动链组成件弹性变形所产生的滚刀轴转角误差之间的比值。可得：

刀架传动链为4轴3齿轮副的3级减速机构，建立计及齿轮副啮合刚度和轴扭转刚度的动力学模型。取传动链中间一对齿轮副进行受力分析，如图3所示。

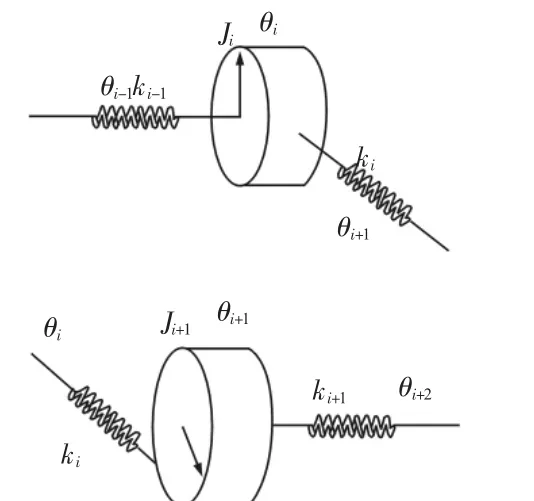
图3 齿轮副受力简图Fig．3 Force Diagram of Gear Pair

假设齿轮制造误差为零，齿廓曲线为标准渐开线，并忽略齿侧间隙和轴承间隙。从图中可以看出每个齿轮既受到由传动轴扭转变形产生的扭矩又受到齿轮副轮齿变形产生的力矩。图中：Ji、Ji+1—两齿轮的转动惯量；ki—两齿轮的啮合刚度；ki-1、ki+1—两轴的扭转刚度。可得两齿轮动力学方程分别为：

式中：rb—齿轮基圆半径。

令：qi=θi-1-θi；qi+1=rbiθi-rbi+1θi+1；qi+2=θi+1-θi+2

即：qn=θn-θn+1n=odd；qn=rbnθn-rbn+1θn+1n=even

初始条件：k1·q1=T

式中：k1—三级齿轮减速机构输入轴扭转刚度；T—减速机构输入转矩。

刀架传动系统，如图1所示。具体结构参数，如表1所示。

表1 结构参数 单位（mm）Tab.1 Structure Parameters

根据式（8），刀架传动系统的机械刚度为：

2.3 伺服刚度建模

伺服系统的伺服刚度和机械刚度是两个不同的概念。伺服刚度是指当存在扰动误差时整个伺服系统，从控制系统到滚刀轴所表现出来的抵抗外力而不产生位置偏差的能力。伺服刚度即为当系统输入信号为0时，干扰信号与其产生的稳态误差值的比值。为了更好的分析伺服刚度，将图2简化变形成方框，如图4所示。

图4 干扰模型传递函数方框图Fig．4 Block Diagram of Interference Model

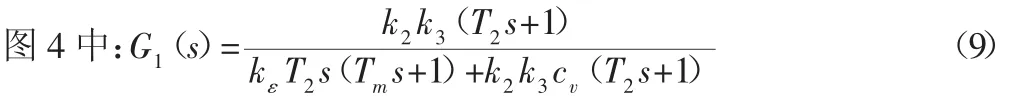
式中：k2—速度环比例增益—速度环积分增益；T—电机时

m间常数。

图4中的反馈通道函数即为扰动点前传递函数G前（S）可得：

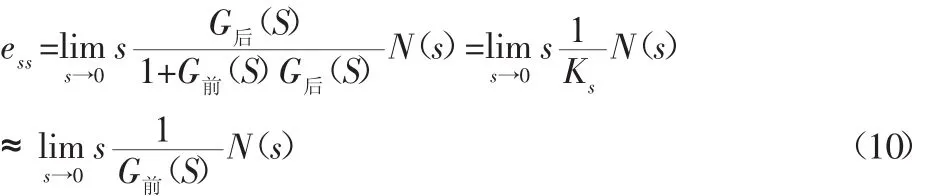
由上式可知，系统由干扰产生的稳态误差与干扰信号的形式和大小有关。而且与扰动作用点前的传递函数的放大倍数成反比。即伺服刚度由扰动点前的传递函数所决定。所以我们只考虑扰动前传递函数的增益值。

G前（S）的增益值为k1k2k3km，所以增大位置环增益k1，增大速度环增益k2k3，或者选用力矩系数大的伺服电机都可以提高Ks。

3 仿真分析

应用Matlab／Simulink对系统进行仿真，根据系统传递函数结构框图从simulink模块库窗口依次选取单元模型，连接后得到系统模型，如图5所示。仿真参数，如表2所示。信号源为单位阶跃信号，从输出模块组中选取示波器模块作为显示器来观察系统阶跃响应。

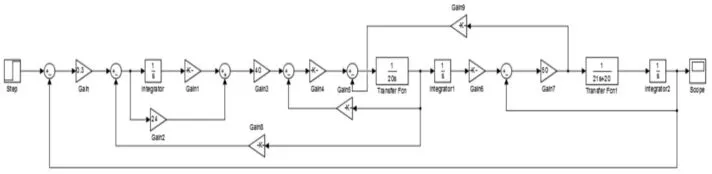
图5 系统的simulink模型Fig．5 System Simulation

表2 仿真参数Tab.2 Simulation Parameters

运行仿真模型，得到的系统阶跃响应特性曲线，如图6实线所示。由仿真分析结果可知，该系统的响应时间为3．1s超调量为15%，动态性能较好。同时也说明了所建模型的正确性。

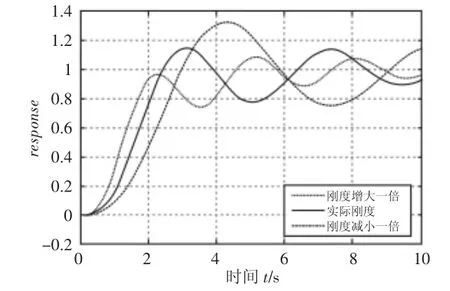
图6 系统的单位阶跃响应Fig．6 Unit-step Response of System

通过改变机械刚度的值来观察机械刚度对系统性能的影响，通过对比分析可得，随着机械刚度的提升，系统的超调量从30%下降到10%，响应时间从4．2s上升到5．1s。而且系统的平滑性变差。由2．2节机械刚度的数学模型可以找出传动链刚度的薄弱环节，有效的增强系统的抗振性能，提高机械刚度，减小弹性变形产生的转角误差，提高传动精度。从系统的仿真分析中可以发现适当提高机械刚度可以改善系统的动态性能，但过大的机械刚度会使系统响应变慢。应综合考虑刚度与系统匹配关系，选取合适的刚度值。在系统的simulink模型上按图4所示加入单位阶跃干扰并令输入信号为0，运行仿真模型，如图7所示。然后改变系统伺服刚度来观察伺服刚度对系统性能的影响。通过对比结果可知，提升系统的伺服刚度，其位置偏差从0．018下降到0．004。极大的增强了系统的抗干扰能力。

图7 系统在干扰下的响应Fig．7 Response of Interference System

另一方面，由于速度误差δv（指令速度V与kv的比值）的存在会影响伺服系统的跟踪精度。

式中：G（S）—系统的前向通道传递函数。

kv和KS是由控制参数决定的，所以kv和KS不能无限增大，当位置环增益增大到一定值后，系统就变得不稳定了。kv和KS同时又受到机械刚度的限制。其匹配条件是：ω＞12ωc。ω是机械装置的谐振频率

4 结论

（1）针对某型滚齿机刀架传动系统，建立了该系统的数学模型。（2）基于静力平衡条件，建立了计及齿轮副啮合刚度、传动轴扭转刚度的传动链等效机械刚度数学模型。得出了传动链每个元件刚度对整体机械刚度的影响因子。（3）运用Matlab／Simulink对系统模型进行了仿真研究，仿真分析了系统的机械刚度对系统的影响。仿真结果表明：机械刚度的提升可以降低系统的超调量但会牺牲一定的响应时间，而且也会令系统的平滑性变差。（4）最后分析了机械刚度、系统伺服刚度及速度误差与系统闭环控制参数之间的匹配关系。得出了参数的限制条件和取值范围。系统在干扰下的仿真结果表明：提高系统的伺服刚度可以增强系统抗干扰能力。

［1］刘丽兰，刘宏昭，吴子英.考虑摩擦和间隙影响的机床进给伺服系统建模与分析［J］.农业机械学报，2010，41（11）：212-218.（Liu Li-lan，Liu Hong-zhao，Wu Zi-ying.Modeling and analysis of machine tool feed servo systems with friction and backlash［J］.Journal of Agricultural Machinery，2011，41（11）：212-218.）

［2］Atsumi T，Arisaka T，Shimizu T.Head-positioning control using resonant modes in hard disk drive［J］.IEEE/ASME Transactions on Mechatronics，2005，10（4）：378-384.

［3］张建伟，张莉军.机械传动部件影响伺服机构性能的因素［J］.机械设计与制造，2001（1）：76-76.（Zhang Jian-wei，Zhang Li-jun.Research on the influence factors of mechanical transmission parts on servo mechanism［J］.Machinery Design&Manufacture，2001（1）：76-76.）

［4］钟掘，陈先霖.复杂机电系统耦合与解耦设计—现代机电系统设计理论的探讨［J］.中国机械工程，1999（9）：1051-1054.（Zhong Jue，Chen Xian-lin.Coupling and decoupling design of complex electromechanical system-discussion on design theory of modern electromechanical systems［J］.Chinese Mechanical Engineering，1999（9）：1051-1054.）

［5］Ebrahimi M，Whalley R.Analysis，Modeling and simulation of stiffness in machine tool drives［J］.Computers&Industrial Engineering，2000（38）：93-105.

［6］Min-SeokKim，Sung-ChongChung.Integrateddesignmethodologyofballscrew driven servomechanisms with discrete controllers Part I modelling and performance analysis［J］.Mechatronics，2006（16）：491-502.

［7］王建明，李萍奎，马术文.数控系统伺服参数对跟随误差影响的研究［J］.机械设计与制造，2011（11）：152-154.（Wang Jian-ming，Li Ping-kui，Ma Shu-wen.Analysis of influence of servo system parameters of CNC on follower error［J］.Machinery Design&Manufacture，2011（11）：152-154.）

［8］刘辉，黄莹，张会杰.数控机床进给系统传动刚度变化对运动精度稳定性的影响规律［J］.机械工程学报，2014（23）：128-133.（Liu Hui，Huang Ying，Zhang Hui-jie.Effects of transmission stiffness variations on the dynamic accuracy consistency of CNC feed drive systems［J］.Journal of Mechanical Engineering，2014（23）：128-133.）

［9］吴子英，刘宏昭，原大宁.某重型车床横向进给系统传动刚度分析与实验研究［J］.实验力学，2011，26（4）：457-463.（Wu Zi-ying，Liu Hong-zhao，Yuan Da-ning.A heavy duty lathe transverse feed system transmission stiffness analysis and experimental research［J］.Experimental mechanics，2011，26（4）：457-463.）

［10］Robert L H，Thomas R B.Starting characteristics of electric submergible oil well pumps［J］.IEEE Transaction on Industry Applications，1986，22（1）：133-144.