五轴数控机床旋转轴转角定位误差建模及补偿
2018-03-21黄奕乔冯文龙沈牧文杨建国
黄奕乔,冯文龙,沈牧文,杨建国
(上海交通大学 机械与动力工程学院,上海 200240)
1 引言
随着现代制造业的不断发展,对具有复杂几何形状的高精度机械零件的需求量大幅增加。由于五轴数控机床具有可加工各种曲面、装夹简便、生产高效、灵活性强等特点,越来越多的五轴数控机床被应用于模具制造、航空部件制造等领域。然而,五轴数控机床的结构复杂,刚度较低,精度低于传统的三轴机床[1]。
目前,五轴数控机床平动轴的定位误差已经被广泛研究[2]。ISO 230-3和ISO 1079-10给出了标准的旋转轴变形测量与辨识方法。常见的旋转轴误差直接检测法有激光干涉仪测量转角定位误差;常见的联动检测方法有球杆仪法[3]、平面光栅法[4]和R-test装置法[5]。旋转轴的各项误差元素中,转角定位误差对加工精度的影响最大[6]。针对旋转轴除转角定位误差之外的与位置相关误差,文献[7]提出了相应的数学模型并补偿,但转角定位误差建模与补偿问题并未涉及。
对旋转轴转角定位误差进行测量,对测量所得的误差值,运用插值节点自适应选择的三次样条插值进行建模,该模型具有拟合精度高、计算简便直观的优点。建立基于数控系统外部坐标原点偏置功能和以太网通讯的误差实时补偿系统,在VMC0656型五轴数控机床上进行补偿实验,验证了模型的正确性和有效性,机床的转角定位精度得到明显提升。
2 基于三次样条插值的转角定位误差建模
运用Renishaw激光干涉仪XR20-W对五轴机床VMC0656旋转轴转角定位误差进行测量,其数据曲线,如图1所示。转角定位误差曲线呈现非线性、变化波动大、正反向形状不同的特点,需要建立相应的数学模型,对其进行拟合。三次样条曲线的光滑性好,通过插值节点的自适应选择,用较少的插值节点实现对非线性、波动大的误差数据的高精度拟合。

图1 C轴转角定位误差测量值Fig.1 Measured Rotary Positioning Error of C-Axis
2.1 三次样条插值模型
在实际工程中,形状曲线由一些离散的数据点来描述大致走向。为了进一步分析曲线,保证一定的光滑性要求,工程中普遍采用样条插值拟合[8]。对曲线参数域[a,b]分段 Δu:a=u0<u1<…<un=b,若实值函数 s(u)满足条件:
(1)每个小区间[ui,ui+1](i=0,1,…,n-1)上是三次多项式;

则称s(u)是f(u)的三次样条插值函数。第i段三次多项式样条插值函数表达式为:
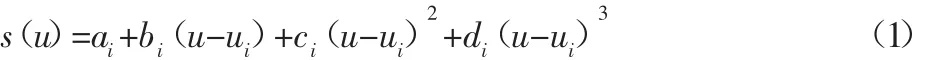
式中:ui≤u≤ui+1,i=0,1,…,n-1;。将连续性条件:

代入三次多项式样条插值函数,得:

式中:hi=ui+1-ui;gi=(Pi+1-Pi)/hi;Pi—第 i个插值节点函数值,Pi=f(ui)。
由式(3)、式(4)和式(5)可解得:

将自然边界条件 s″(u0)=s″(un)=0 代入式(6),可解得三次样条插值函数表达式。
2.2 插值节点自适应选择
运用样条插值的方法进行数据处理时,要求在给定的逼近容差范围内,用尽可能少的插值节点逼近数字化数据描述的原始几何,因此要求作为插值节点的数据点能很好地表达数据的几何信息[9]。
对旋转轴转角定位误差测量获得的误差数据点Pi(i=0,1,…,m)运用均匀参数化法进行参数化,获得参数值ui,以及各数据点的曲率信息ki。三次样条插值节点自适应选择算法选用两个端点和局部最大曲率点作为插值根节点。局部最大曲率点[10]需要满足要求:ki>ki-1,且 ki>ki+1。局部最大曲率点按照曲率 ki大小进行排序。两个端点和曲率值最大的前n-1个局部最大曲率点作为n+1个插值节点,代入三次多项式样条插值算法获得初始插值函数s(u)。为了保证插值模型精度,令初始插值函数的预测残差:
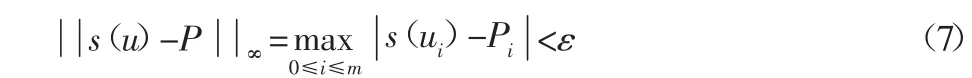
式中:i=0,1,…,m;s(ui)—模型预测误差值;
Pi—误差实际测量值;
ui—数据点Pi的参数化值;
ε—模型预测容许残差。
若式(7)成立,即初始插值函数的预测残差满足容许残差要求,则建模完成;若式(7)不成立,将残差超过容许残差的误差数据点添加为新的插值节点,得到新的三次样条插值模型,并根据式(7)对新模型进行精度判定。重复此过程直到模型残差满足精度要求,算法结束,获得旋转轴转角定位误差的三次样条插值模型。三次样条插值节点自适应选择算法流程图,如图2所示。

图2 三次样条插值节点自适应选择算法流程图Fig.2 Algorithm Flow Chart of Cubic Spline Interpolation Nodes Adaptive Selection
2.3 正反双向转角定位误差模型
由图1可知,在旋转运动方向不同时,正、反向转角定位误差曲线形状相差较大,并存在交叉点,仅通过反向间隙补偿效果不佳。需要对正、反向误差曲线分别进行三次样条插值建模,以此进行双向补偿。

图3 正、反向转角定位误差模型预测值与测量值比较Fig.3 Comparison Between Measured and Predicted Rotary Positioning Error of Forward and Backward Direction
运用节点自适应选择的三次样条插值算法对正、反向转角定位误差曲线进行建模。正、反向误差曲线的预测误差值、测量误差值以及两者相减所得的建模残差,如图3所示。可见正、反向转角定位误差模型的拟合精度非常高,分别为1.2″和-0.86″。
3 补偿实施及其结果
利用数控系统的外部坐标原点偏置功能和以太网数据通讯功能,自主研发了误差补偿系统,并在双转台五轴机床VMC0656上进行试验,对转角定位误差进行补偿,并将三次样条插值模型与其他常见的误差拟合模型进行了对比分析。
3.1 误差补偿系统
开发的误差补偿系统结构,如图4所示。补偿系统的硬件平台使用嵌入式计算机,通过数控机床以太网接口与Fanuc 31i数控系统进行通讯。数控系统可编程机床控制器(PMC)中的原点偏移功能将与实际误差大小相等、方向相反的误差补偿值信号叠加到伺服控制信号中,实现误差补偿。一个补偿循环可以在8ms之内完成,Fanuc 31i数控系统的以太网数据交互速度为100Mbps,可以满足误差误差补偿实时性的要求。补偿系统的结构,如图8所示。

图4 补偿系统结构框架图Fig.4 Schematic Diagram of Compensation System
补偿流程为:
(1)将测量仪器获得的误差测量文件导入补偿软件;
(2)补偿软件通过以太网交互方式读取PMC中的机床旋转轴坐标值和伺服运动方向信息;
(3)误差预测模型以误差测量值、机床坐标值和伺服运动方向作为输入,输出误差预测值;
(4)通过以太网交互方式向PMC输出误差预测值;(5)PMC模块通过外部坐标系原点偏移功能将误差补偿值与NC程序叠加,误差补偿值与误差预测值大小相等、方向相反。PMC将原点偏移叠加后的NC程序输出到伺服控制器中,实现旋转轴转角定位误差的正反向实时补偿。
3.2 实验验证与模型对比
在VMC0656型五轴数控机床上进行了误差补偿实验。目前数控系统自带的螺距误差补偿功能可实现平动轴和旋转轴的定位误差补偿,输入测量点的测量误差值即可实现补偿;但由于旋转轴正、反向转角定位误差曲线形状差异较大,并存在交叉点,螺距误差补偿功能无法实现对正、反向转角误差分别进行误差补偿值输入,因此补偿效果较差。使用开发的误差补偿系统进行实验,安装,如图5所示。为了比较三次样条插值建模方法和其他常用误差建模方法的差异,分别使用六次多项式模型、斜线插值模型、非均匀有理B样条(NURBS)插值模型和三次样条插值模型进行补偿,四种模型的补偿结果,如图10、表1所示。其中三次样条插值和非均匀有理B样条插值模型的补偿精度最高,斜线插值模型和六次多项式模型补偿效果较差。

图5 误差补偿系统安装图Fig.5 Installation of Compensation System
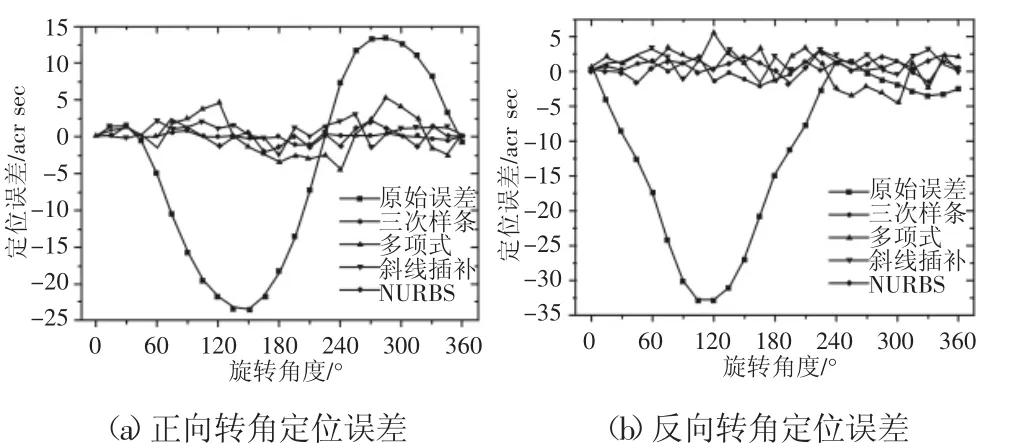
图6 不同模型转角定位误差补偿前后对比Fig.6 Comparison of Rotary Errors with and without Compensation by Different Models
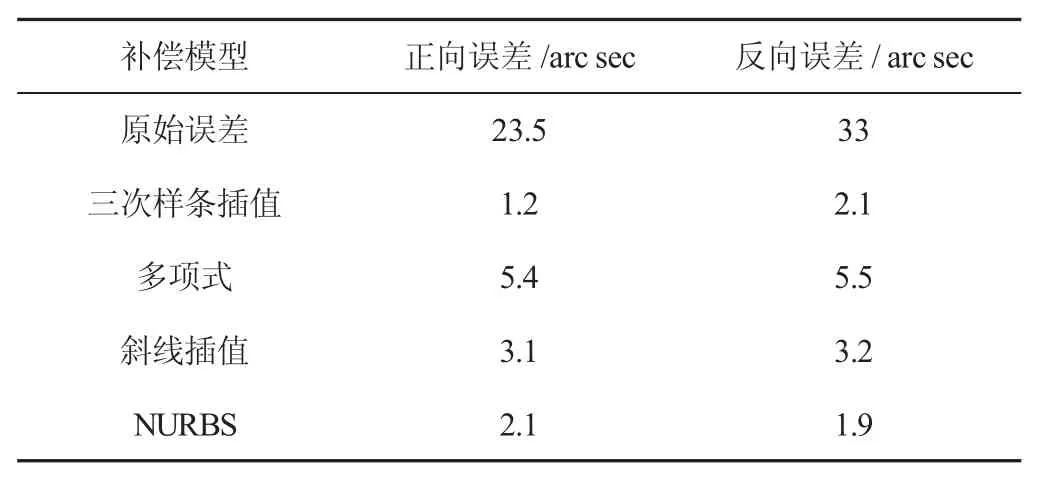
表1 不同模型补偿前后转角定位误差值Tab.1 Rotary Errors with and without Compensation by Different Models
多项式模型通过最小二乘法对误差数据进行拟合,其优点是可以保证转角定位误差拟合曲线二阶导数的连续性,避免速度和加速度突变;但多项式模型的拟合精度较低,并存在高阶过拟合现象,不易获得较高的补偿精度。
斜线插值使用各测量点的测量误差值进行补偿,各测量点之间使用直线连接,插值曲线在插值点处导数不连续,补偿时会导致速度和加速度的突变,影响补偿效果。
NURBS插值模型使用B曲线作为基函数进行分段插值,其优点是插值点处可以保证误差拟合曲线二阶导数连续,避免速度加速度突变,补偿效果好;但其求解过程复杂,计算量较大。
三次样条插值模型可以保证误差曲线的二阶导数连续,避免速度和加速度突变;每段插值曲线为三次多项式,表达式简洁直观;通过自适应插值节点的选取,在满足插值精度的前提下,尽可能减少插值节点数,减少了计算量;结合旋转轴转动方向进行双向补偿,解决了正、反向误差曲线差异大、有交叉的问题。通过补偿实验验证,转角定位误差降低了94%,补偿效果很好。
4 结论
(1)建立了基于Fanuc数控系统外部坐标原点偏移功能和以太网通讯的误差实时补偿系统,结合三次样条插值误差预测模型对五轴数控机床旋转轴转角定位误差进行了补偿。
(2)建立了基于三次样条插值的旋转轴转角定位误差预测模型,通过插值节点的自适应选择,保证模型拟合精度和计算速度;
(3)结合旋转轴运动方向,对转角定位误差进行正反双向建模与补偿,补偿结果表明:转角误差降低了94%。
[1]Ramesh R,Mannan M,Poo A.Error compensation in machine tools—a review:Part II:thermal errors[J].International Journal of Machine Tools and Manufacture,2000,40(9):1257-1284.
[2]关贺,杨建国.数控机床体积定位精度的测量与补偿[J].机械设计与制造,2003(1):78-81.(Guan He,Yang Jian-guo.Measurement and compensation of volumetric positioning errors for CNC machines[J].Machinery Design and Manufacture,2003(1):78-81.)
[3]Ihara Y.Ball bar measurement on machine tools with rotary axes[J].International Journal of Automation Technology,2012,6(2):180-187.
[4]Du Zheng-chun,Zhang Shu-jie,Hong Mai-sheng.Development of a multi-step measuring method for motion accuracy of NC machine tools based on cross grid encoder[J].International Journal of Machine Tools and Manufacture,2010,50(3):270-280.
[5]Ibaraki S,Oyama C,Otsubo H.Construction of an error map of rotary axes on a five-axis machining center by static R-test[J].International Journal of Machine Tools and Manufacture,2011,51(3):190-200.
[6]Hong C,Ibaraki S,Matsubara A.Influence of position-dependent geometric errors of rotary axes on a machining test of cone frustum by five-axis machine tools[J].Precision Engineering,2011,35(1):1-11.
[7]Gebhardt M,Thermal Behaviour and Compensation of Rotary Axes in 5-Axis Machine Tools[M].Diss.,Eidgenossische Technische Hochschule ETH Zürich,Nr.21733(2014):2014.
[8]Wahba G,Spline Models for Observational Data[M].Siam:1990.
[9]田锡天.五次样条在数控加工中的全过程应用技术[D].西安:西北工业大学,2003.(Tian Xi-tian.Application of quintic spline interpolation in numerical controlprocessing[D].Xi’an:NorthwesternPolytechnicalUniversity,2003.)
[10]陈露.基于特征性质的三次B样条拟合算法[D].大连:大连理工大学,2009.(Chen Lu.Cubic B-spline fitting method based on dominant information[D].Dalian:Dalian University of Technology,2009.)
