粘弹性层厚度对复合材料夹芯梁自由振动的影响

翟彦春，王绍清，梁 森

（青岛理工大学 机械工程学院，山东 青岛 266520）

1 引言

在当今的工业领域，比如帆桅杆以、机器人手臂及直升飞机机翼等等，复合材料结构在其整体结构中的使用比例正变得越来越高。这是因为复合材料的大量应用在最大化的降低结构的重量的同时还能极大地提高结构的强度、可设计性以及疲劳寿命。帆桅杆、机器人手臂、风力发电机叶片及直升飞机机翼等类似结构可以近似的看成是复合材料层合梁结构[1-3]。

国内外许多学者专家对这一结构进行了研究。文献[4]在高阶剪切理论的基础上基于有限元模型研究了不同边界条件和边长比下的复合材料梁的自由振动；文献[5]基于Kirchhoff-Love理论和C1型有限元模型研究了梁的弯曲振动；在文献[5]的基础上，考虑横向剪切变形影响的基础上，又研究了梁的自由振动[6]。文献[7]基于渐进数值方法结合有限元模型对复合材料结构进行了研究；文献[8]基于有限元模型，采用一阶折线理论对五层复合材料梁的阻尼特性进行了研究；文献[9]应用三节点有限元模型分析了层合梁的自由振动，使用正弦函数表征了沿厚度方向振动位移的变化规律，使用余弦功能函数表征了横向剪切应变，得到了正弦振动模型。文献[10]建立了复合材料薄壁梁的模型及非线性平衡方程，得到了在不同铺层角度下时间位移曲线和非线性振动幅度随铺层角的变化情况；文献[11]分别使用FSDT和HSDT对四边简支矩形复合材料三明治板的自然振动进行研究，结果表明这两种理论对于分析中厚三明治板的动态特性具有较高的准确性。文献[12]使用扩展哈密尔顿原理和瑞利-里兹法研究了包含增强型主动约束阻尼层的对边简支梁的模型频率和损耗因子。

由于经典的欧拉-伯努利梁理论忽略了梁在振动过程中的剪切变形的影响，使得对于中厚板的振动计算中精度不够，因此，考虑剪切变形影响的铁木辛柯梁理论被采用。在之前研究的基础上，基于铁木辛柯梁理论结合哈密尔顿原理推导了粘弹性复合材料梁的振动平衡方程，并通过与公开发表的文献的计算数据对比，验证方程推导的正确性，最后研究了粘弹性层厚度对阻尼层复合材料梁的振动平衡方程的影响，即对构件的频率和损耗因子的影响，得到的结论可为工程人员设计复合材料梁提供参考。

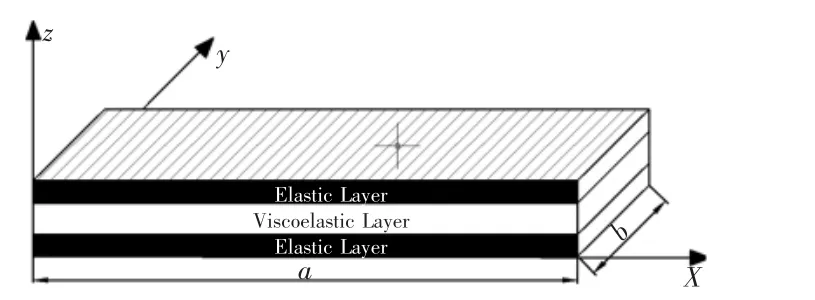
图1 粘弹性复合材料梁结构Fig．1 Structure of Viscoelastic Layer Composite Beam

2 振动平衡方程的推导

铁木辛柯梁理论位移模型：

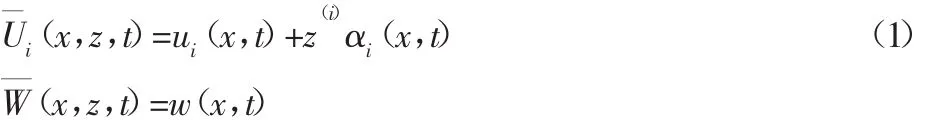
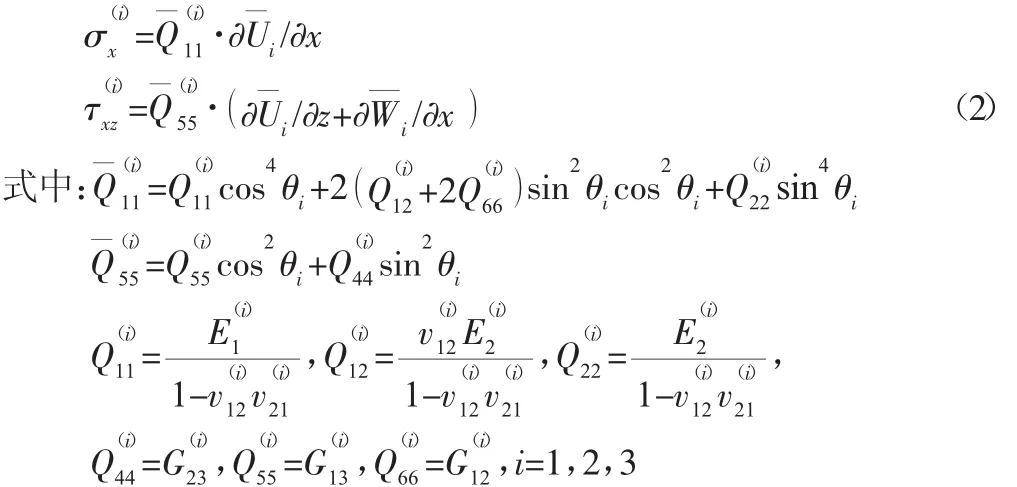
根据弹性体动力学的哈密尔顿原理，粘弹性复合材料梁结构的自由振动的变分方程为：

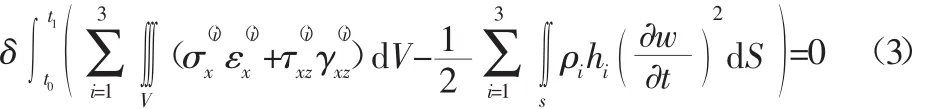
由于面内位移较横向位移小得多，为简化计算，只考虑横向位移的动能。将式（2）、带入式（3），整理可得振动平衡方程。

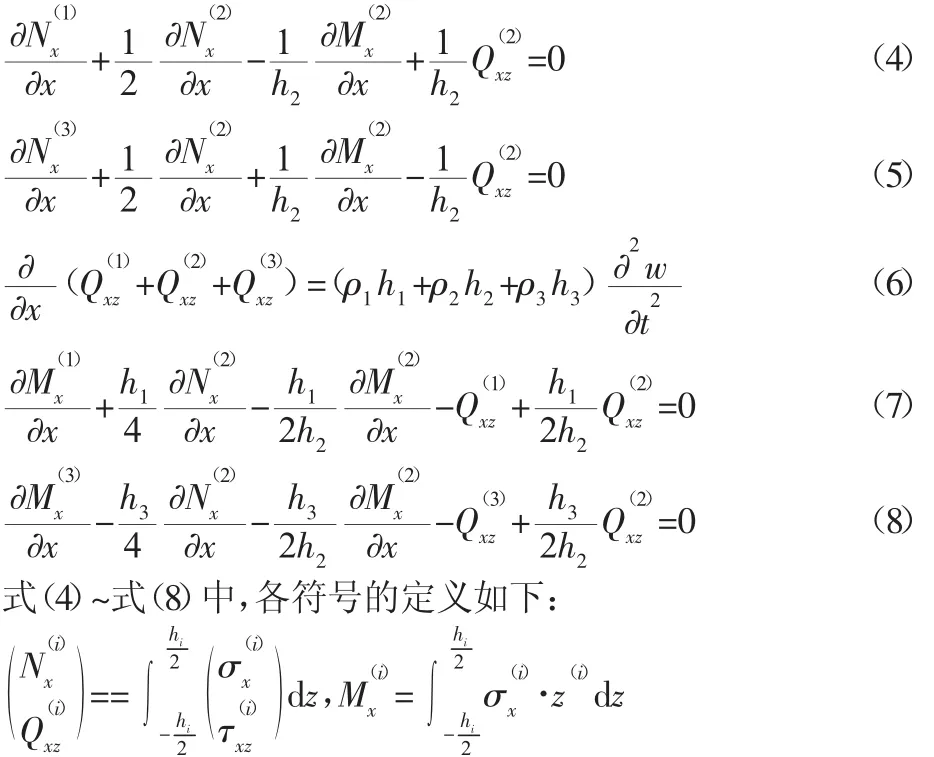
3 振动分析

3.1 模型验证

采用Navier型解法，使用MATLAB软件对满足对边简支边界条件的（0°/90°/0°）铺设的阻尼层复合材料梁的振动平衡方程进行求解。文献[13]中的模型尺寸为：长度为300mm，表层和底层梁的厚度分别为 0．5mm 和 5mm，他们的密度都是 7．8×103kg/m3，并且他们的弹性模量同为E=207×109Pa；阻尼层厚度hc=2．5mm，密度为 2×103kg/m3，剪切模量 G*=0．2615MPa，损耗因子 0．38。经计算得到的固有频率和损耗因子的对照结果，如表1、表2所示。

从表1和表2可以看出，固有频率的计算误差都在5%以内，损耗因子的误差都在9%以内，说明所推导的公式是正确的。之所以存在一定的误差，在于和文献[13]采用的计算方法不同，采用Navia型解法，而文献中采用的是广义微分积分法。

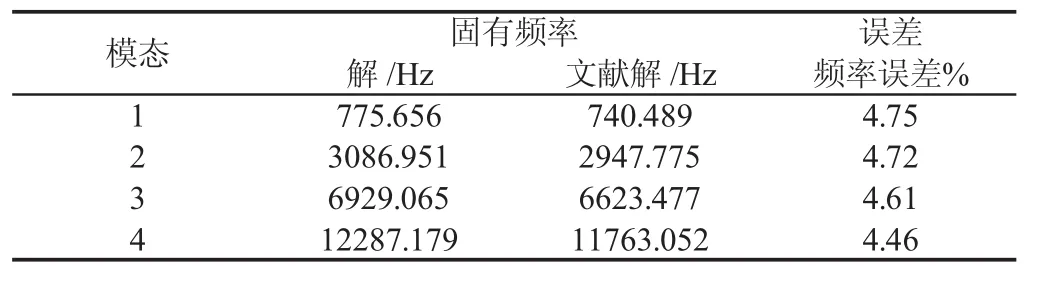
表1 固有频率对照表Tab.1 Contrast of Inherent Frequency

表2 损耗因子对照表Tab.2 Contrast of Loss Factor

3.2 弹性层厚度不定，阻尼层厚度对自振的影响

保持弹性层梁的厚度不变，通过改变粘弹性层梁的厚度来探究阻尼层厚度对频率和损耗因子的影响，如表3和表4所示。

从表3和表4可以看出，随着阻尼层厚度的增大，损耗因子值逐渐增大，而固有频率的值逐渐减小。并且一阶固有频率和四阶损耗因子的变化区间最大，而四阶固有频率和一阶损耗因子的变动最小，基本趋于直线状态。

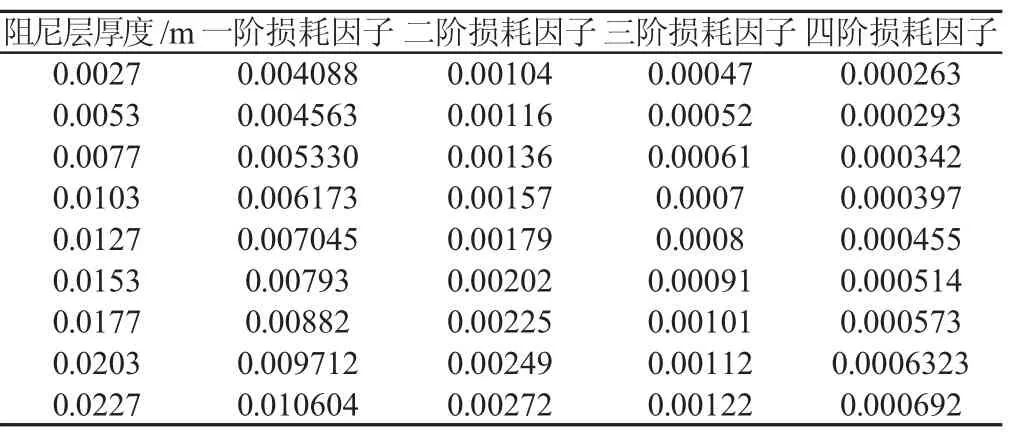
表3 阻尼层厚度对损耗因子的影响Tab.3 Influence of Damping Layer Thickness on Loss Factor

表4 阻尼层厚度对固有频率的影响Tab.4 Influence of Damping Layer Thickness on Inherent Frequency

3.3 总厚度不定，阻尼层厚度对自振的影响

在保持粘弹性复合材料梁总厚度不变的前提下，逐渐增大阻尼层的厚度，同时复合材料层的厚度会逐渐减小。在此种计算情况下，梁的结构参数如下：总厚度=80mm，底层和表层的厚度相等，性能参数不变，计算结果，如表5、表6所示。

从表5和表6中可以看出，前四阶固有频率的变化趋势随厚度的增大而减小，变化趋势与上一种情形相同，但是变动区间更大，呈现急剧下降的趋势。

损耗因子变化趋势在阻尼层厚度值小于0，005时基本不变，变化较平缓，但是当厚度大于0.005时，整体构件的损耗因子值急剧增大，并且越接近阻尼层的损耗因子值。

表5 阻尼层厚度对固有频率的影响Tab.5 Influence of Damping Layer Thickness on Inherent Frequency

表6 阻尼层厚度对损耗因子的影响Tab.6 Influence of Damping Layer Thickness on Loss Factor

4 结论

基于铁木辛柯梁理论位移模型，推导了阻尼层复合材料梁的振动平衡方程，使用Navier型解法验证了所推导方程的正确性，其次分两种情况研究了阻尼层厚度对复合材料梁的自由振动的影响，结果表明：

（1）分别保持梁的复合材料层厚度不变和总厚度不变的情况下，都是随着阻尼层厚度的增大，前四阶固有频率逐渐降低，损耗因子值逐渐增大。

（2）梁的总厚度不变时，前四阶固有频率随阻尼层厚度的增大而减小，变动区间较大，呈现急剧下降的趋势；损耗因子在阻尼层厚度值小于总厚度的一半时基本不变，变化较平缓，但是当厚度大于总厚度的一半时，整体构件的损耗因子值急剧增大，并且越接近阻尼层的损耗因子值。

［1］Mead D J.The effect of a damping compound on jet-efflux excited vibrations：an article in two parts presenting theory and results of experimental investigation part i the structural damping due to the compound［J］.Aircraft Engineering and Aerospace Technology，1960，32（3）：64-72.

［2］曹岩，沈冰，刘红军.某太阳能无人机复合材料机身结构梁选型与优化［J］.机械设计与制造，2016（7）：205-208.（Cao Yan，Shen Bing，Liu Hong-jun.Selection and optimization of new solar uav composite fuselage structural beams［J］.Mechinery Design&Manufacture，2016（7）：205-208.）

［3］江舒扬，蔡晶，傅洁.夹芯复合材料风力机叶片的结构设计方法［J］.机械设计与制造，2014（1）：33-36.（Jiang Shu-yang，Cai Jing，Fu Jie.Structural design method of sandwich composite wind turbine blade［J］.Mechinery Design&Manufacture，2014（1）：33-36.）

［4］Marur S R，Kant T.Free vibration analysis of fiber reinforced composite beams using higher order theories and finite element modelling［J］.Journal of Sound&Vibration，1996，194（3）：337-351.

［5］Ahmed K M.Free vibration of curved sandwich beams by the method of finite elements［J］.Journal of Sound&Vibration，1971，18（1）：61-74.

［6］Ahmed K M.Dynamic analysis of sandwich beams［J］.Journal of Sound&Vibration，1972，21（3）：263-276.

［7］Akoussan K，Boudaoud H，Carrera E M E.Vibration modeling of multilayer composite structures with viscoelastic layers［J］.Mechanics of Advanced Materials&Structures，2015，22（1-2）：136-149.

［8］Adessina A，Hamdaoui M，Xu C.Damping properties of bi-dimensional sandwich structures with multi-layered frequency-dependent viscoelastic cores［J］.Composite Structures，2016（154）：334-343.

［9］Vidal P，Polit O.Vibration of multilayered beams using sinus finite elements with transverse normal stress ［J］.Steel Construction，2010，92（6）：1524-1534.

［10］朱由锋，薛风先.复合材料薄壁箱梁的非线性自由振动分析［J］.机械设计与制造，2015（1）：7-10.（Zhu You-feng，Xue Feng-xian.Non-linear free vibration analysis of composite thin-walled box beams［J］.Mechinery Design&Manufacture，2015（1）：7-10.）

［11］Meunier M，Shenoi R A.Free vibration analysis of composite sandwich plates［J］.ARCHIVE Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science，1999，213（7）：715-727.

［12］Gao J X，Liao W H.Vibration analysis of simply supported beams with enhanced self-sensing active constrained layer damping treatments［J］.Journal of Sound&Vibration，2005，280（1-2）：329-357.

［13］Arikoglu A，Ozkol I.Vibration analysis of composite sandwich beams with viscoelastic core by using differential transform method［J］.Composite Structures，2010，92（12）：3031-3039.