基于广义霍夫变换的粘连字符验证码的识别

汪志华

(集美大学计算机工程学院，福建 厦门 361021)

0 引言

验证码最初是一种用于区分用户是计算机还是人的测试程序，它通过生成测试并对用户作答进行评判,后来，逐渐发展成为网站防范攻击的一种安全技术而受到广泛的应用。按照内容划分，验证码主要分为字符验证码、图像验证码、声音验证码等。字符验证码具有生成成本低、答案比较确定、对用户友好等优点，目前被大多数网站采用。由于普通字符验证码容易被程序自动识别，为提高网站安全性，在生成字符验证码时，可以通过增加干扰线条、扭曲字符、粘连字符、旋转字符、混合不同字体的字符等方法，增大验证码自动识别的难度。本文研究的对象即为此类具有粘连字符、旋转字符的验证码。

粘连字符验证码的识别难度较大，对于粘连字符验证码的识别，大多数研究者主要采用字符分割、特征提取、字符识别等流程。如：王璐等[1]基于局部极小值和最小投影值的方法来分割字符，然后采用卷积神经网络进行训练和识别，但对于粘连字符验证码的识别率只有38%；张亮等[2]采用水平和垂直投影进行字符分割，然后通过递归神经网络进行识别，对不同测试集识别率在20%～60%之间；唐海涛[3]提出一种基于PNN-SOINN-RBF网络构建的自组织增量神经网络模型对验证码进行识别，该方法的识别率在60%～85%之间，对于一些测试集可以达到95%；汪洋等[4]采用轮廓差投影法与水滴算法对验证码进行字符切割，然后利用KNN算法进行字符识别，识别率为81%；陈以山等[5]利用传统的数字图像形态学处理技术对可分割字符的验证码进行识别，识别率约为60%；尹龙等[6]提出基于密集尺度不变特征变换和随机抽样一致性算法的识别方法，能够较好地处理一般性的粘连字符，其识别率为88%，并对于扭曲粘连较严重的验证码也取得了一定的实验成果；Wang Ye等[7]提出基于自适应的算法来对验证码图像进行去噪和分割，并利用OCR和模板匹配的方法来识别分割后的字符；Garg Geetika等[8]利用CNN和RNN组建深度神经网络来对文本验证码进行识别，对于字符数确定和不确定的验证码识别率分别达到99.8%和81%。

验证码的识别需要综合数字图像处理、机器学习、人工智能等学科知识。研究验证码的识别可以发现验证码设计的漏洞，有助于改进验证码的设计，提高网站的安全性，防范恶意批量操作和暴力破解数据库等行为。同时验证码的识别技术也可以用于车牌识别、光学字符识别、手写字识别等领域。目前大部分识别方法对于可分割的验证码识别效果较好，但在处理粘连字符时由于无法准确地进行字符分割，使系统的识别正确率受到影响。因此，研究验证码的识别特别是粘连字符验证码的识别具有一定的理论和实践意义。

1 基于广义霍夫变换的验证码识别

本文提出一种基于广义霍夫变换(generalized Hough transform,GHT)的识别方法。首先将验证码图片和模板图像进行预处理和骨架化，对模板图像中的图像边缘像素点提取两个局部特征(重心夹角和重心距离)作为参考表中的内容，再对验证码图片中的每个像素根据其与参考表的匹配情况进行投票，从而确定验证码中是否存在模板图像，进而达到字符识别的目的，最后通过干扰分析，来剔除形状类似的字符对识别结果的干扰。系统的识别结构如图1所示。

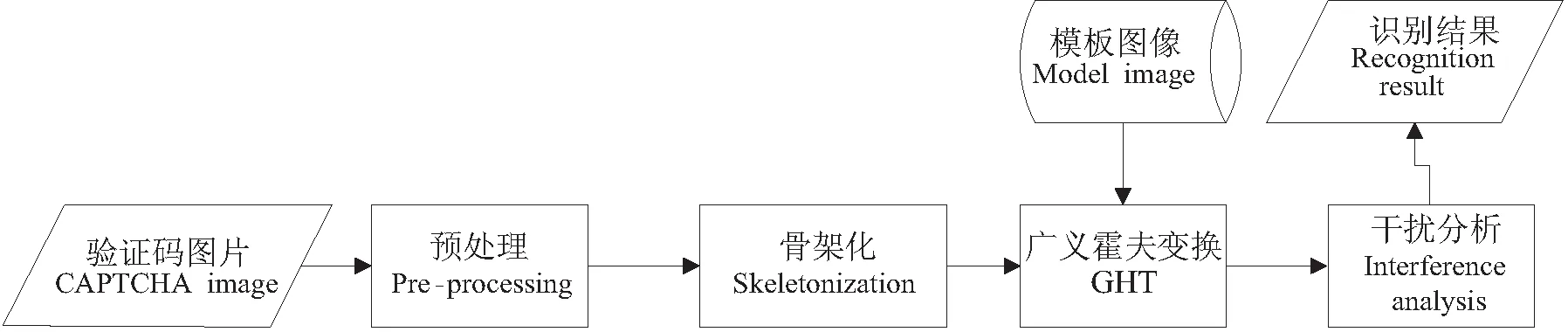
图1 验证码识别结构图

1.1 预处理

验证码图片一般为彩色图像，为降低计算复杂度，需要将其灰度化，并转换成二值图像进行处理。灰度化转换公式为Y=0.3R+0.59G+0.11B。图像转换成灰度图后，采用最大类间方差法(Otsu)将图像分为前景和背景两部分。在Otsu算法中用类间方差作为标准来衡量前景和背景，类间方差越大，说明两者的差别就越大，错分的概率也就越小[9]。设图像的总像素数为N，前景的像素点数为N0，前景所占总像素的比例为P0，且P0=N0/N，前景的平均灰度值为U0，背景的像素点数为N1，背景所占总像素的比例为P1，且P1=N1/N，背景的平均灰度值为U1，则图像的总体平均灰度值U=P0U0+P1U1，类间方差δ2=P0(U-U0)2+P1(U-U1)2。因此，分割阈值T就是使得δ2取得最大值的阈值。图像预处理的结果如图2所示。

1.2 骨架化

骨架由曲线及弧线构成，它是物体的中轴，是对物体形状特征的一个描述方法。骨架一般宽度为单个像素，它接近图像的位置中心，对边缘噪声不敏感，可以表达出人对物体形状描述的视觉特征。本文采用Zhang快速并行细化算法[10]来寻找字符的骨架，该算法具有运算速度快，细化后的曲线保持连通性等优点。

设二值图像中，目标点标记为1，背景点标记为0，则定义边界点标记为1且其8-连通邻域中至少有1个标记为0的点。图3所示为二值图像中像素P1的8-连通邻域。

算法对边界点进行以下两次迭代[10]：

大渡河长河坝砾石土心墙堆石坝坝高240 m，建于覆盖层最大厚度79.3 m的地基上，处于高地震烈度区，100年超越概率2%基岩水平峰值加速度为0.359 g。该工程采用两道全封闭混凝土防渗墙，在主防渗墙顶设置了城门洞型式的廊道与心墙连接，如图1(a)、图1(b)所示，廊道内部尺寸3 m×4 m，侧墙厚2 m，底板厚3 m。该廊道在河床段沿纵向不设结构缝，原设计在基岩覆盖层分界线处分缝与两岸灌浆平洞连接，但采用类似结构的跷碛及瀑布沟等工程均出现了廊道开裂及止水破坏的现象[3-4]。经深入研究后，坝基廊道改为深入基岩1 m与两岸灌浆平洞有缝连接[5]，如图1(c)所示。

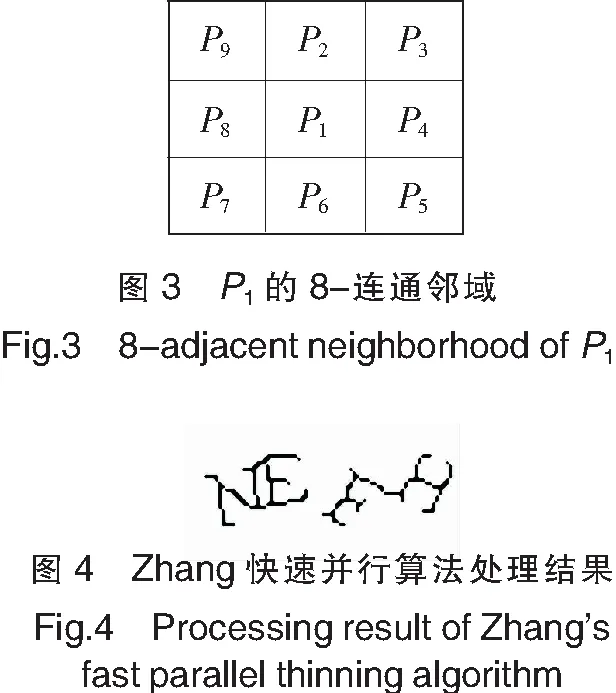
1)第一次迭代，若P1满足下列4个条件，则进行标记。①2≤N(P1)≤6，N(P1)表示P1非0邻点的个数；②S(P1)=1，S(P1)表示按P2,P3,…,P9排列时，出现01模式的个数；③P2×P4×P6=0；④P4×P6×P8=0。当迭代完成后，清除所有标记了的点。

2)第二次迭代，标记满足条件的点P1。P1也需要满足4个条件，前两个条件即第一次迭代的条件①和条件②，第三个条件为P2×P4×P8=0，第四个条件为P2×P6×P8=0。当迭代完成后，清除所有标记了的点。

重复上面两次迭代，直到没有点满足标记条件，则剩下的点就是目标的骨架。对图2c应用Zhang快速并行细化算法[10]进行处理的效果如图4所示。

1.3 广义霍夫变换

当图像被处理成骨架后，可以把字符看成具有一定形状的物体，因而可以通过广义霍夫变换来搜索在验证码图片中是否出现了某个字符及其出现的位置。

1.3.1 广义霍夫变换的原理

在广义霍夫变换[11]中，任意形状可以定义为：

ω(θ,b,λ,ρ)=b+λR(ρ)ν(θ),

(1)

其中：ν表示模板的曲线定义，b=(x0,y0)是平移向量，λ是尺度因子，R(ρ)是旋转矩阵。因此，形状的位置由式(2)给出：

b=ω(θ)-λR(ρ)ν(θ)，

(2)

假设称ωi=(ωxi，ωyi)为图像上的点，那么：

b=ωi-λR(ρ)ν(θ),

(3)

式(3)定义了1个具有4个未知量的方程系统，将图像点映射到累加器空间，通过检查图像点与模板图像的特征是否匹配，从而收集获得目标形状的证据。

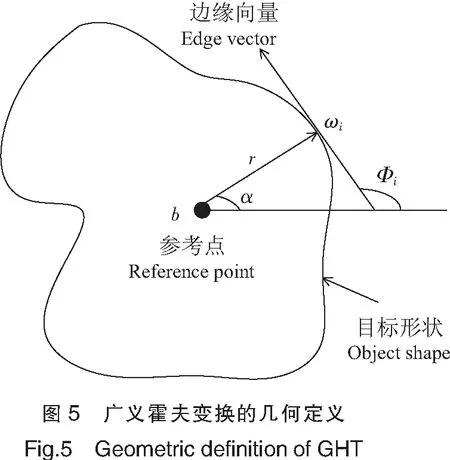
广义霍夫变换的几何定义如图5所示，其映射函数的极坐标方程可以表示为：

b=ω(θ)-reα，

(4)

其中，Φ(θ)=arctan(y(θ)/x(θ))，α=Φ(θ)+ρ，r=λΓ(θ)，Γ(θ)=sqrt(x(θ)×x(θ)+y(θ)×y(θ))。

1.3.2 模板图像的R-表结构

由于模板图像为任意的形状，没有简单的曲线方程能够描述，在广义霍夫变换中采用了建立R-表(参考表)来描述参考点和边缘点的关系。本文选取模板字符的重心作为参考点，将边缘像素点的重心夹角和重心距离记录到参考表中。重心夹角指模板图像边缘像素点与模板图像重心连线形成的向量的方向角，即图5中的α。重心距离指模板图像边缘像素点与模板图像重心之间的距离，即图5中的r。重心夹角与重心距离具有平移和旋转的不变性，但不具有尺度不变性，因此选取的特征无法处理缩放字符的识别。参考表的结构如表1所示。

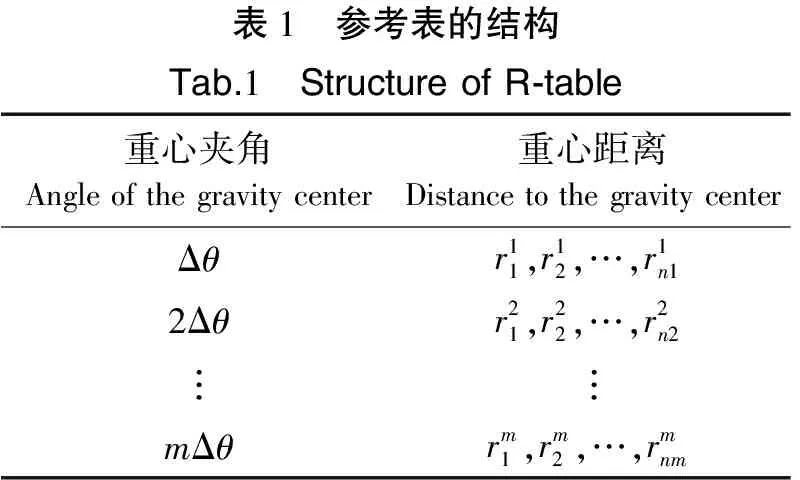
表1 参考表的结构Tab．1 StructureofR⁃table重心夹角Angleofthegravitycenter重心距离DistancetothegravitycenterΔθr11，r12，…，r1n12Δθr21，r22，…，r2n2︙︙mΔθrm1，rm2，…，rmnm

1.3.3 证据收集算法

对骨架化后的验证码图像上的目标像素点，根据模板图像的R-表进行评价，得到参考点的坐标，然后对累加器数组进行累加投票，最后将投票的极大值输出即得该模板图像的参考点(重心)位置。 设骨架化后的验证码图像和模板图像记为I和Q，I的大小为M×N，Q的参考表记为RTable，重心夹角记为A，投票累加器数组记为a，大小为M×N，累加器阈值记为T，该阈值表示在I中与Q相似的目标点数量的最小值，如果累加器的数值超过此阈值，可以认为在I中存在Q。证据收集的算法如下：

1) 顺序取出模板图像Q以及它的参考表RTable；

2) 投票累加器数组a清零；

3) 对验证码图像I中的所有目标点(x,y)，遍历所有的重心夹角A(0≤A<2π，增量为Δθ)，计算参考点的坐标(x0,y0)；

4) 如果(x0,y0)合法，则a[x0,y0]增1；

5) 扫描累加器数组，如果a[i,j]为极大值，且a[i,j]≥T，则(i,j)即为模板图像Q的重心，输出该模板对应的字符、重心坐标(i,j)以及投票累加器的值a[i,j]。

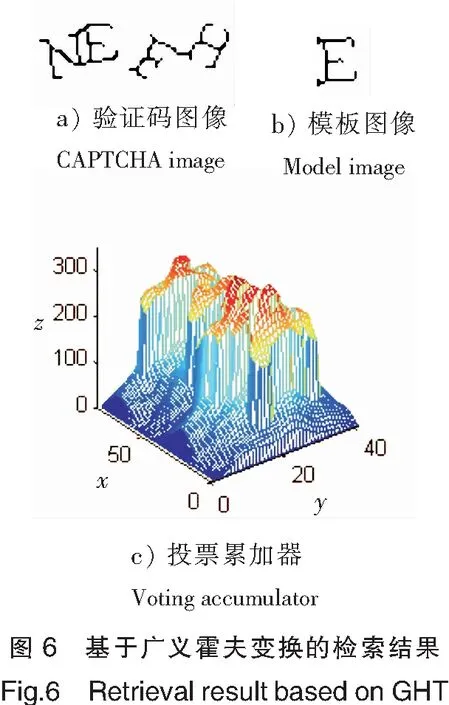
基于广义霍夫变换对验证码图像进行检索的结果如图6所示。图6a为骨架化后的验证码图像，图6b为骨架化后字符模板图像，图6c为使用模板图像在验证码图像中进行检索后得到的投票累加器，该累加器在(27,16)具有极大值且累加器的数值大于阈值T，说明在验证码中出现了字符E，且重心坐标为(27,16)。

1.4 干扰分析

由于字符之间的相似性，在验证码图像中检索目标字符时会产生重复识别的情况。例如，如果验证码中含有字母“B”，则广义霍夫变换也会检测出字母“P”，因此需要对这种相似性导致的识别干扰进行排除。当两个字符的距离很近时，这时就出现了干扰，此时需判断两者的累加器数值，累加器数值大的获胜，因为这意味着有更多的目标点类似于该模板图像。

干扰分析的算法如下：

1)将广义霍夫变换识别的结果按照重心x坐标从小到大排列。

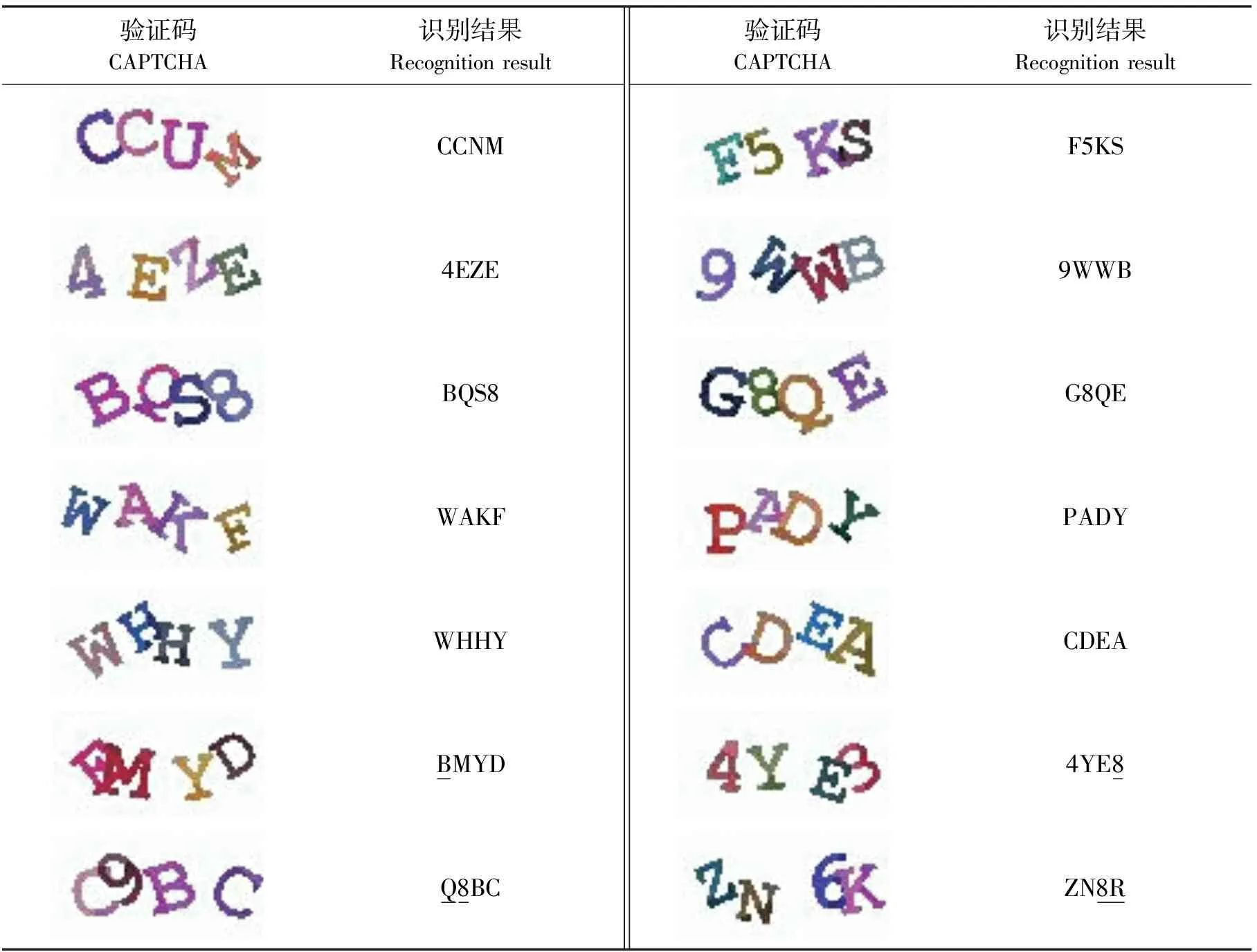
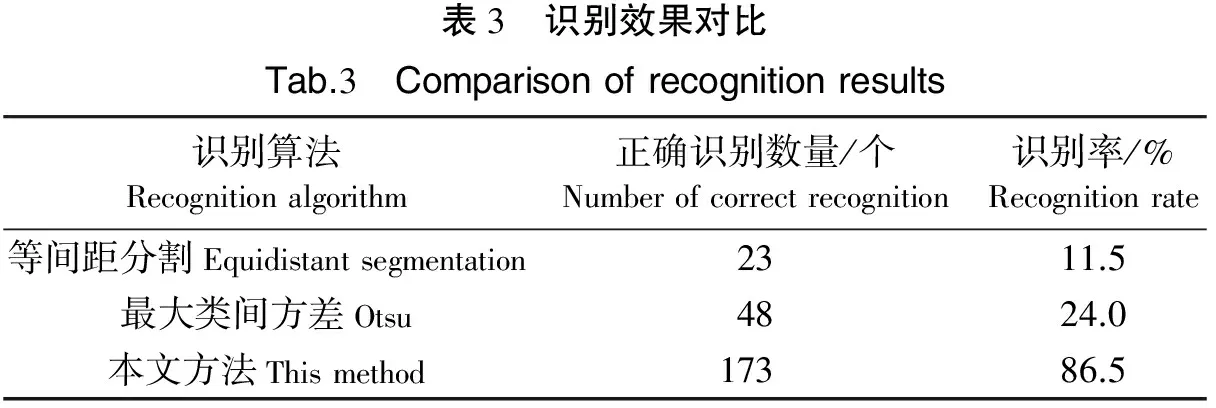
2)遍历上述数组，如果某字符c1与紧邻的字符c2重心之间的横向距离d=|x1-x2|

3)按重心x坐标从小到大输出对应的字符，此即为验证码识别结果。

2 实验结果

本文采用自主测试集，测试集包括200张验证码图像，图像中以英文大写字母和数字0～9为字符集，每个图片包含4个字符，每个字符随机旋转1个角度，旋转角度介于-40°到+40°之间，每个字符颜色随机。部分识别结果如表2所示，其中字符的下划线表示该字符识别错误。

表2 部分识别结果

从实验结果来看，本文提出的方法能够正确识别具有字符旋转、字符轻微粘连的验证码，但如果字符粘连严重，则邻近字符的干扰增大，导致识别正确率下降。由于在GHT中，需要对验证码图像中的所有目标点根据公式(4)计算参考点的坐标，如果字符粘连严重，则相邻的目标像素就会对累加器数组进行累加计数，影响正确的参考点的坐标，从而导致字符的识别错误。

表3 识别效果对比Tab．3 Comparisonofrecognitionresults识别算法Recognitionalgorithm正确识别数量/个Numberofcorrectrecognition识别率/%Recognitionrate等间距分割Equidistantsegmentation2311．5最大类间方差Otsu4824．0本文方法Thismethod17386．5

作为对比，本文选用等间距字符分割法和最大类间方差法两种传统的字符分割方法与本文方法一起对验证码图像进行分割，再用ABBYY FineReader OCR软件来识别分割后的字符。实验对比结果如表3所示，其中测试集为200张验证码图像。从结果可以看出，传统方法的实验识别率较低，原因主要有3点：1)由于验证码中的每个字符都有1个随机的旋转变换(旋转角度-40°～+40°)，经过等间距分割或类间最大方差分割后，没有对字符进行倾斜纠正，而直接由该OCR软件识别，因此识别率较低；2)由于验证码中字符的旋转导致一些字符粘连在一起，无论等间距分割或类间最大方差分割都无法将字符正确分割开，因而导致该OCR软件无法正确识别；3)验证码的识别是需要将图片中4个字符都成功识别，才算成功，只要有1个字符识别错误，则判定为错误。如果字符正确地进行了分割，该OCR软件对单个字符的识别率可以达到90%以上，但对仅轻微旋转或受扰的字符的正确识别率大概只有50%～75%。在验证码分割中由于字符的粘连，总有个别字符识别效果很差，从而使得整体的识别率非常低。因此传统字符分割再识别的方法无法适应粘连字符验证码的识别，而本文方法则比较有效。

3 结束语

针对粘连字符验证码，本文提出了一种基于广义霍夫变换的识别方法，该方法通过对字符模板和验证码图片进行二值化和骨架化，通过对字符模板的每个目标点像素抽取局部特征建立参考表。对于验证码图片，采用像素逐点匹配和投票的方式进行广义霍夫变换，最后对相邻字符间的干扰进行分析，排除干扰字符。由于采取重心夹角和重心距离等局部特征具有平移和旋转不变性，因此本算法能够处理字符局部形变和字符旋转。并且广义霍夫变换不需要对验证码图片进行分割，它能够适应并有效处理字符轻度粘连的情况，具有一定的抗干扰性。但本算法中选择的局部特征不具备尺度不变性，因此本方法不适用于字符具有缩放、形变或粘连严重的验证码识别。

[1]王璐,张荣,尹东,等.粘连字符的图片验证码识别[J].计算机工程与应用,2011,47(28):150-153.

[2]张亮,黄曙光,石昭祥,等.基于LSTM型RNN 的CAPTCHA识别方法[J].模式识别与人工智能,2011,24(1):40-47.

[3]唐海涛.自组织增量神经网络的验证码识别模型与算法[D].广州: 广东工业大学,2016.

[4]汪洋,许映秋,彭艳兵.基于KNN 技术的校内网验证码识别[J].计算机与现代化,2017(2):93-97.

[5]陈以山,张勇.基于字符的图片验证码识别算法的设计与实现[J].电脑知识与技术,2017,13(1):190-192.

[6]尹龙,尹东,张荣,等.一种扭曲粘连字符验证码识别方法[J].模式识别与人工智能，2014,27(3):235-241.

[7]WANG YE,LU MI.A self-adaptive algorithm to defeat text-based CAPTCHA[C]//2016 IEEE International Conference on Industrial Technology.Taipei:IEEE,2016:720-725.DOI:10.1109/ICIT.2016.7474839.

[8]GARG GEETIKA,POLLETT CHRIS.Neural network CAPTCHA crackers[J].IEEE Conference Proceedings,2016,FCT:853-861.

[9]瞿中.基于改进的最大类间方差算法的图像分割研究[J].计算机科学,2009,36(5):276-278.

[10]章毓晋.图像工程：中册 图像分析[M].2版.北京：清华大学出版社,2005:222-223.

[11]MARK S NIXON,ALBERTO S AGUADO.特征提取与图像处理[M].2版.李实英，杨高波,译.北京:电子工业出版社,2010:179-185.