分数阶非线性Schrödinger方程的时间分裂算法
2018-03-21,
,
(集美大学理学院,福建 厦门 361021)
0 引言
分数阶微积分的计算是一个古老而新鲜的研究领域,特别是近年来,分数阶偏微分方程在数学,生物,化学,医学,控制理论,信号和图像处理,以及物理中的应用受到越来越广泛的关注。因为分数阶微分算子在很多地方比整数阶微分算子更贴近实际,如分数阶微分算子具有的非局限性,使得它能较好地用于描述事物的记忆性以及遗传性质。在数值计算方面,由于分数阶微分方程的解析解或者很难显式给出,或者含有特殊函数,使其计算相当困难。所以,用数值方法模拟其解是一个自然的想法,也使得分数阶偏微分方程的数值解法成为国内外研究的热点之一,很多学者对此也已取得了一定的研究成果,如:文献[1-2]对时间分数阶慢扩散问题,用G-L逼近建立了向前Euler差分格式和加权差分格式,并分析了两种差分格式的稳定性;文献[3-4]对慢扩散方程初边值问题建立了几个隐式差分格式,并分析了差分格式的稳定性和收敛性;文献[5]对该问题进行数值离散,分析了差分格式的逼近误差,并用Fourier方法分析了所得差分格式的无条件稳定性;文献[6]对时间分数阶扩散方程提出在时间方向采用有限差分,在空间方向采用谱方法,并证明了时间方向上(2-α)阶收敛,而空间方向上具有谱精度;文献[7]对时间分数阶导数,用换元法将一个高阶方程转化成低阶扩散方程组来逼近并构造其差分格式,且严格证明了时间方向上的收敛阶为(2-α)阶。
作为经典的Schrödinger方程,其数值解法一直是学者关注的热点之一,由应用而扩展出的分数阶Schrödinger方程,也有不少成果,如:文献[8]针对线性分数阶Schrödinger方程提出了配点法;文献[9]对Hartree方程提出了时间分裂拟谱法。这些研究主要集中在线性方程,对分数阶非线性微分方程还没有太多的数值解法,文献[10]通过能量方法研究了分数阶非线性Schrödinger方程光滑解的整体唯一性;文献[11]则对耦合非线性分数阶Schrödinger方程给出了Crank-Nicolson(C-N)格式。
本文利用分裂算法来研究一维分数阶非线性Schrödinger方程,将原方程分裂成一个线性方程和一个非线性方程。对线性方程采用C-N格式离散,其中Riesz分数阶导数-(-Δx)α/2u采用了中心差分算子近似。对非线性方程利用其“点点守恒”的特性可精确求解。本文提供了一种分步计算方法,首先证明了该分裂算法在离散意义下保持了原方程所具有的质量及能量守恒性,也证明了格式的收敛性和稳定性,收敛精度为二阶精度,且无条件稳定。最后利用数值例子验证了质量及能量的守恒性及收敛精度,理论和数值都表明,该方法是一个简单有效且守恒的新的算法。
1 分数阶非线性Schrödinger方程
本文考虑如下分数阶非线性Schrödinger方程初边值问题:
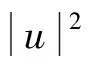
(1)
u(x,0)=u0(x),a≤x≤b,
(2)
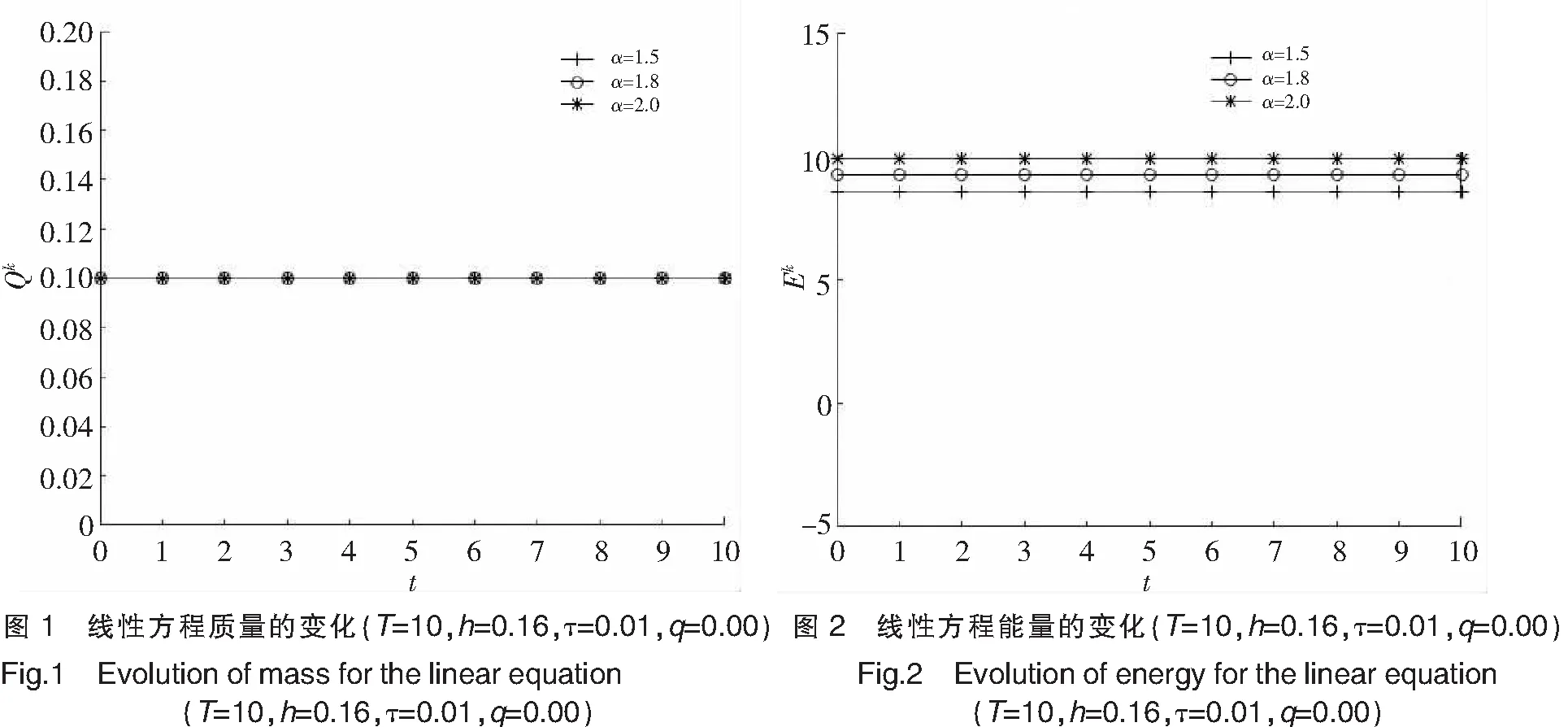
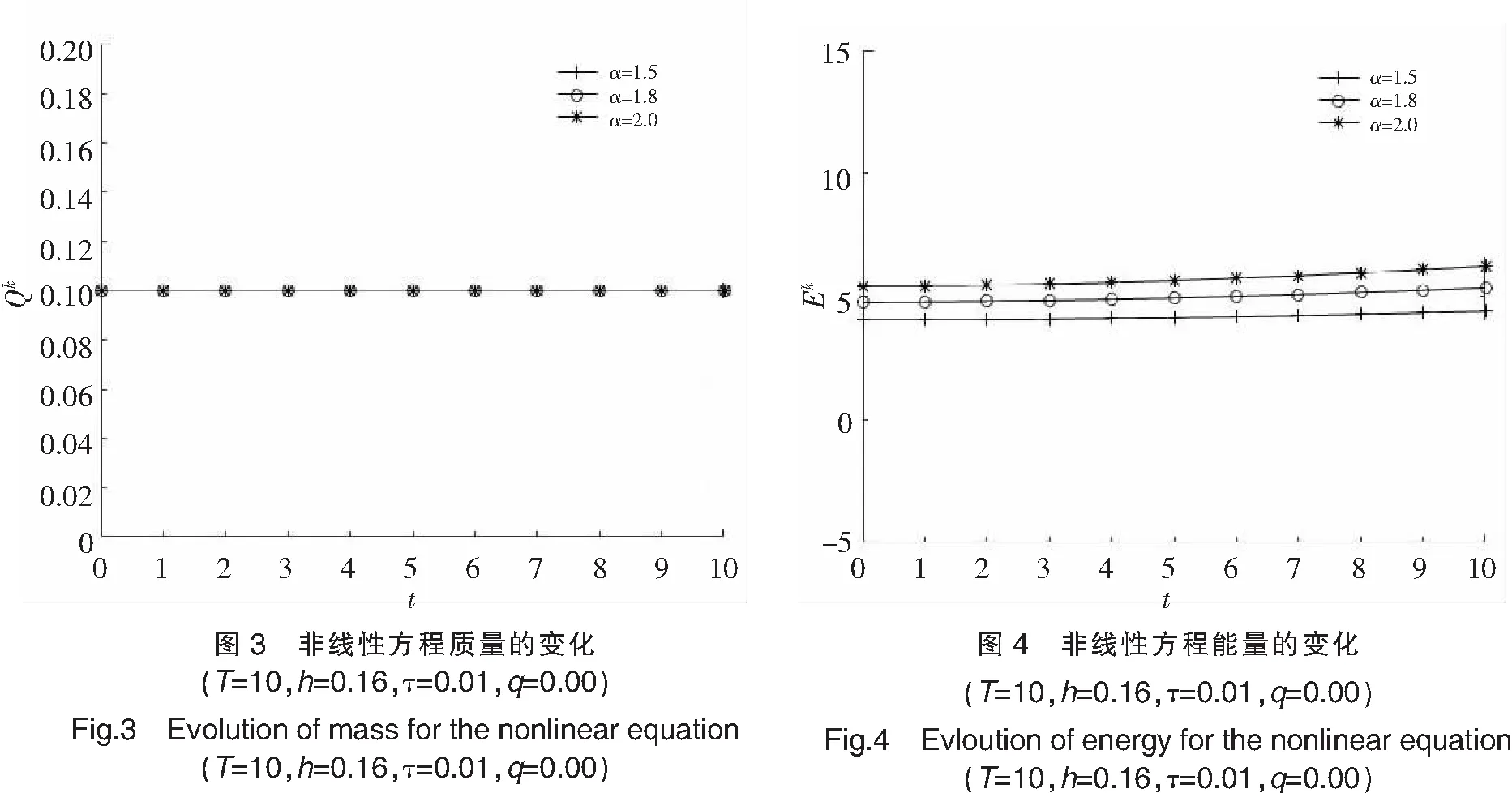
u(a,t)=u(b,t)=0, 0 (3) (4) 引理1[13]设u(x,t)是问题(1)~(3)的解,问题(1)~(3)具有质量守恒Q(t)和能量守恒E(t)两个守恒律。 Q(t)=Q(0), 0≤t≤T,E(t)=E(0), 0≤t≤T。 (5) 一个算法的好坏,除了精度、收敛速度、稳定性问题之外,还有一个很重要的指标,即构造的格式是否很好地模拟了原方程具有的特性,如守恒性。 引理2 对于0<α≤2,Riesz分数阶导数-(-Δx)α/2u中心差分算子定义[2]如下: 因为当x∈(-∞,a)∪(b,+∞)时,u*(x,t)=0,从而 (6) (7) 对于分数阶非线性Schrödinger方程,采用时间分裂方法。 对时间变量从t=tn到t=tn+1,将式(1)分裂为两个方程来进行分步计算。 第一步是计算线性方程 i∂tu(x,t)-(-Δx)α/2u(x,t)=0,a (8) 其满足齐次边界条件式(3)。 第二步是计算非线性方程 (9) (10) 即 (11) 对式(9)在(tn,t)上积分,并利用式(11)得 u(x,t)=eiq|u(x,tn)| 2(t-tn)u(x,tn),a (12) 对线性方程式(8),考虑如下的Crank-Nicolson差分格式,并利用引理1得 (13) (14) (15) (16) (17) 将式(15)改写成 (18) 记μ=τ/(2hα),式(18)也可写成(I+iμCx)U(2)=(I-iμCx)U(1)的矩阵表示形式,于是对式(1)可建立如下时间为二阶的分步计算格式: (19) (I+iμCx)U(2)=(I-iμCx)U(1), (20) (21) (22) (23) 该分裂算法是一个守恒的格式,即在离散意义下满足质量和能量守恒这一原方程的特性。由Cx的性质可知(I+iμCx)可逆,于是 U(2)=(I+iμCx)-1(I-iμCx)U(1)=HU(1), (24) 其中H∶=(I+iμCx)-1(I-iμCx)。 引理4 矩阵H是酉矩阵(H*为H的酉共轭矩阵)。 证明因为Cx对称,(I+iμCx)-1与(I-iμCx)可交换,H*=(I-iμCx)*((I+iμCx)-1)*=(I+iμCx)((I+iμCx)*)-1=(I+iμCx)(I-iμCx)-1=(I-iμCx)-1(I+iμCx),所以HH*=I,故H是酉矩阵。 (25) 图1和图2分别表明了α各种取值状态下的质量值和能量值,从图1和图2可以看出,其质量值Qk和能量值Ek基本保持了一个数值,且质量值Qk与α的取值无关,而能量值Ek则与α相关,与理论完全相吻合,同时时间步长和空间步长取得较大。 对于分数阶非线性Schrödinger方程,取q=1,从图3和图4可以看出,该数值格式也保持了质量和能量的守恒。同时注意到,该计算格式是在取得步长较大的情况下进行模拟的,数值结果仍然保持了非常好的稳定性,这也很好地说明了该格式的优越性。 对于非线性方程,取时间区间为[0,1],α分别取1.3,1.6及2,计算相同时间步长及空间步长下能量的误差值及误差的阶,阶的计算公式为:order=log2(e(τ1,h1)/e(τ2,h2))。从表1中可以看出阶的精度达到O(h2+τ2),完全符合理论结果。由表1还可以看出,随着α值的增加,阶的精度在提高,表明其收敛阶与α有关,具体需进一步研究讨论。 表1 T=1,q=1时不同的α,τ,h计算出的能量误差 αh=0.2,τ=0.2h=0.1,τ=0.1h=0.05,τ=0.051.3eEOrder1.229548e-014.279556e-021.52261.451656e-021.59361.6eEOrder7.481111e-02 1.630393e-022.19803.502252e-032.21892.0eEOrder3.549441e-02 3.954015e-033.16624.641902e-043.0905 本文对分数阶非线性Schrödinger方程构造了一个守恒的数值格式,对分数阶微分算子Riesz分数阶导数利用中心差分算子进行了离散,利用二阶时间分裂算法将一非线性问题转化成了一线性子问题和一可精确求解的非线性子问题。从数值实例中也可以看出,该方法简单有效,并保证了原方程的质量守恒和能量守恒,且可以取大步长的,无条件稳定的,其精度为二阶精度。该方法不仅适用于一维问题,而且多维问题及耦合分数阶非线性方程也可以采用该算法进行数值模拟。下一步将继续深入研究,致力于寻找更高效率、高精度的数值解法。 [1]YUSTE S B.Weighted average finite difference method for fractional diffusion equations[J].Comput Phys,2006,216:264-274.DOI:10.1016/j.jcp.2005.12.006. [2]YUSTE S B,ACEDO L.An explicit finite difference method and a new von Neumann-type satability analysis for fractional diffusion equations[J].SIAM J Numer Ana,2005,42:1862-1874.DOI:10.1137/030602666. [3]CHEN C M,LIU F,ANH V,et al.Numerical schemes with high spatial accuracy for a variable-order anomalous subdiffusion equations[J].SIAM J Sci Comput,2010,32:1740-1760.DOI:10.1137/090771715. [4]ZHUANG P,LIU F,ANH V,et al.New solution and analytical techniques of the implicit numerical method for the anomalous subdiffusion equations[J].SIAM J Numer Anal,2008,46:1079-1095.DOI:10.1137/060673114. [5]LANGLANDS T A M,HENRY B I.The accuracy and stablility of an implicit solution mehod for the fractional diffusion equations[J].Comput Phys,2005,205:719-736.DOI:10.1016/j.jcp.2004.11.025. [6]LIN Y M,XU C J.Finite difference/spectral approximation for the time fractional diffusion equations[J].Comput Phys,2007,2(3):1533-1552.DOI:10.1016/j.jcp.2007.02.001. [7]SUN Z,WU X.A fully discrete difference scheme for a diffusion-wave system[J].Appl Numer Math,2006,56(2):193-209.DOI:10.1016/j.apnum.2005.03.003. [9]BAO W Z,DONG X C.Numerical mathods for computing guound state and dynamics of nonlinear relativestic Hartree equation for boson stars[J].J Comut Phys,2011,230:5449-5469.DOI:10.1016/j.jcp.2011.03.051. [10]郭柏灵,蒲学科,黄凤辉.分数阶偏微分方程及其数值解[M].北京:科学出版社,2011. [11]WANG D L,XIAO G A,YANG W.Crank-Nicolson difference scheme for the coupled nonlinear Schrödinger equation with Riesz space fractional derivative[J].J Comput Phys,2013,242:670-681.DOI:10.1016/j.jcp.2013.02.037. [12]孙志忠,高广花.分数阶微分方程的有限差分方法 [M].北京:科学出版社,2015. [13]WANG D L,XIAO A G,YANG W.A linearly implicit conservative difference scheme for the space fractional coupled nonlinear Schrödinger equations[J].Comput Phys,2014,272:644-655.DOI:10.1016/j.jcp.2014.04.047.
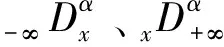
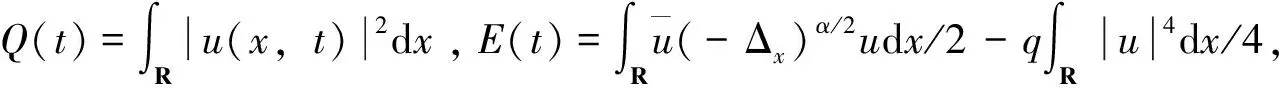
2 时间分裂算法
2.1 记号

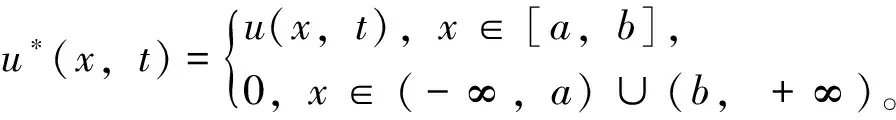
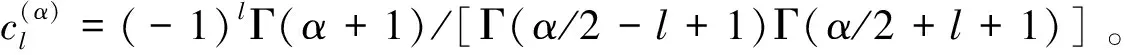
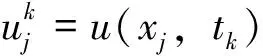

2.2 分数阶非线性Schrödinger方程时间分裂方法



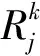
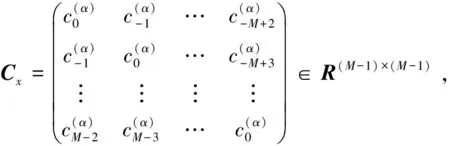

2.3 分裂算法解的守恒性


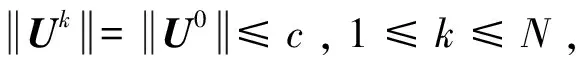


2.4 分裂算法的收敛性
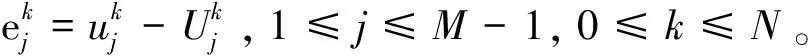
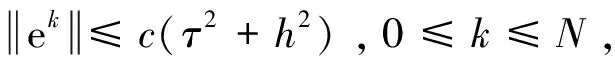
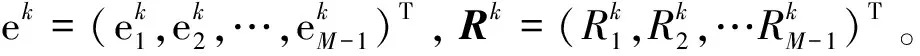
3 数值实验


4 结论
