年龄结构、产出效率和经济增长关系的理论与实证

2018-03-21朱波侯亚楠

统计与决策 2018年4期

朱波，侯亚楠

（山西财经大学统计学院，太原030006）

0 引言

近年来，我国人口老龄化问题备受关注。人口老龄化进程逐步加快，使得我国的劳动力缺口和养老金支付压力日趋增大。对此，一些学者认为延迟退休是应对人口老龄化的必然之举[1,2]，客观分析老年人的劳动生产率和收入分配机制，是有效探索延迟退休经济影响的关键。

截至目前，国内学者关于劳动生产率和劳动收入的研究很少涉及年龄因素。张晓青（2009）[3]基于扩展的Cobb-Douglas生产函数研究山东县域经济和人口数据，认为劳动生产率随年龄增长而呈显著下降趋势。魏下海等（2012）[4]对中国家庭营养与健康调查数据（CHNS）进行分析，认为年龄—劳动收入呈“倒U”型曲线，峰值在55岁左右。徐升艳和周密（2013）[5]研究我国2000年和2005年的城市相关数据，认为东部和中部城市60～64岁年龄组的劳动生产率高于15～19岁年龄组，延迟退休有助于开发老年人的劳动力资源。可见，我国年龄—劳动生产率曲线形状如何尚无定论，年龄—劳动收入曲线形状如何也无文献可征。

因此，本文借鉴HNT模型的研究框架，重点分析年龄—劳动生产率、劳动收入曲线的四种典型特征及各情形下延迟退休年龄对经济增长和就业的影响，并基于我国1987—2016年间宏观经济和人口数据对构建的理论模型进行实证分析，研究结果具有一定的理论和现实意义。

1 理论研究

1.1 生产函数

为了便于分析，本文假定产出主要取决于劳动和资本两个生产要素，并采用扩展的Cobb-Douglas生产函数：

其中，Q为产出；A为技术水平；K为资本投入；L为劳动力人数，λL为有效劳动投入。

假定：①不存在“退而不休”和“提前退休”现象；②各年龄组劳动者是可以完全替代的。则根据Stoeldraijer等（2010）[6]及Mahlberg（2013）[7]的研究成果，有效劳动投入可以表示为：

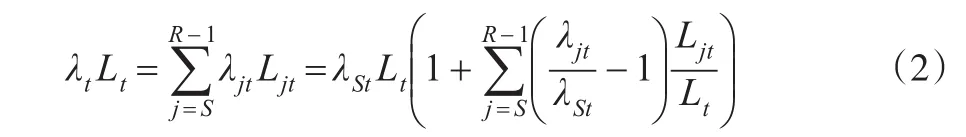
其中，S表示起始工作年龄；R表示退休年龄；Lj表示j年龄组劳动力人数，选择LS为参照组，则有不同年龄组边际产出的比值为：

若假定生产函数规模报酬不变(α+β=1)，对生产函数（1）两边取对数，可调整为便于实证分析的回归模型：

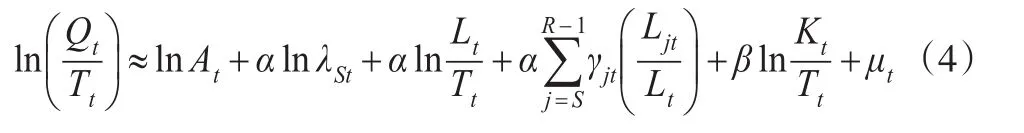
其中，T为总人口；γjt=(λjtλSt-1)，表示j年龄组劳动者与新入职劳动者的边际产出相对差距；αγjt反映了就业人口中j年龄组人口占比每增加1个百分点，人均产出的相对增长速度。

1.2 劳动收入

在市场出清假定下，一般认为劳动的边际产出等于工资收入。然而，老年人的经济负担、再就业成本要远远高于年轻人，使得工会、社会保障等部门更多关注老年人的收入和就业保障[6]。因此，本文假定企业发放工资时，有两种方式可以选择：一是按劳分配，按照劳动者的边际产出发放工资；二是按资分配，按照劳动者的资历（本文特指年龄）发放工资。

在按劳分配模式下，劳动的边际产出等于劳动收入，则有：

在按资分配模式下，企业首先根据全体劳动者的平均边际产出计算平均工资，然后根据各职工的工作年限具体发放工资：

其中，MP为劳动者的平均边际产出；Wjt为j年龄组劳动者的劳动收入为全部人口为基数计算的人均劳动收入；f()取决于按工龄计发工资的具体模式，一般可选择线性函数、指数函数或二次函数等。

不管是何种收入分配模式，人均劳动收入Wˉ都可以表示为：

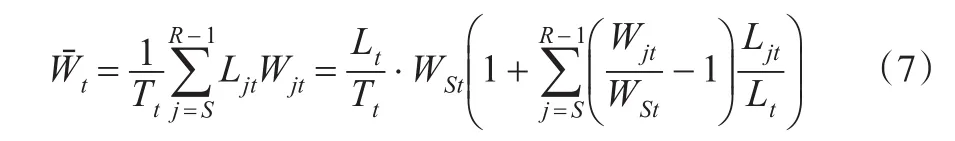
则有：

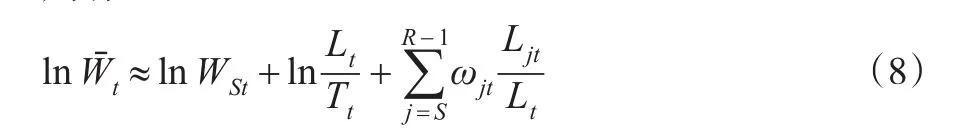
若假定劳动者边际产出、劳动收入的相对差距每年基本保持不变，则有“γjt=γj”和“ωjt=ωj”。比较γj和ωj的大小，可以研究劳动生产率和劳动收入差距如何随年龄增长而变化。由于模型（4）和模型（8）是两个独立的模型，为了合理比较γj和ωj，可将模型（4）两边同时除以α，并与模型（8）两边相减，经过整理后可得模型：

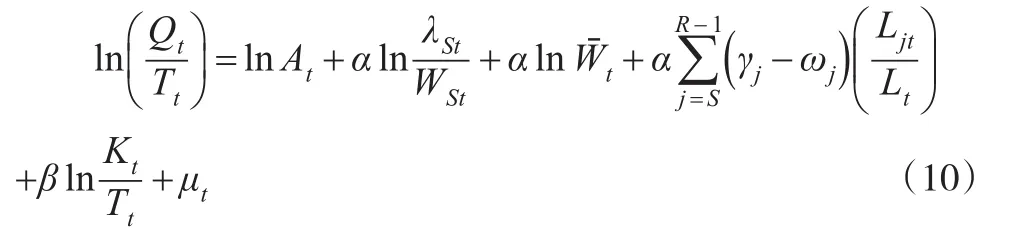
可见，若劳动力市场出清，劳动的边际产出等于劳动收入（γ=ω），则人均产出主要取决于技术进步、平均边际产出（平均劳动收入）和人均资本投入；若劳动力供给明显大于需求（存在人口红利），劳动的边际产出一般高于劳动收入（γ＞ω），则人均产出将呈现更快的增长速度。

1.3 典型情形下延迟退休的经济影响

1.3.1 按劳分配模式

情形1（图1左）：年龄—劳动生产率曲线呈“倒U”形状，峰值在退休后

由模型（10）可知，若γ=ω，则延迟退休对人均产出增长速度的影响主要由劳动者的平均边际产出水平来决定。由于劳动生产率的峰值出现在退休年龄之后，退休年龄从R延迟到R+1，平均劳动生产率将显著提高，则人均产出增长速度将显著提升。此时，若总产出超过全社会的需求能力，则延迟退休将冲击年轻人就业。

情形2（图1右）：年龄—劳动生产率曲线呈“倒U”形状，峰值在退休前

此情形下，延迟退休对就业和经济增长的影响，关键取决于新延退的老年人与新成长劳动力的边际产出相对差距γR。若γR＞0，则延迟退休将冲击年轻人就业，但有助于提高人均产出的增长速度。若γR＜0，企业只有增加对年轻人的雇佣，增加就业人数，才能提高以总人口为基数计算的平均边际产出水平，进而维持人均产出的合理增长速度。

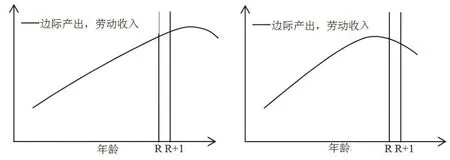
图1 按劳分配时年龄—劳动生产率、劳动收入曲线典型形状

1.3.2 按资分配模式

情形3（下页图2左）：年龄—劳动生产率曲线呈“倒U”形状，峰值在退休后

由模型（9）可知，若γ≠ω，则延迟退休对人均产出增长速度的影响将由边际产出与劳动收入差距、劳动者年龄结构和平均边际产出水平共同决定。在按资分配情形下，对于老年人，γ＜ω；对于年轻人，γ＞ω。因此，延迟退休在提高劳动年龄人口平均劳动生产率的同时，也将因为企业对老年人薪酬的过度支付而抑制经济增长。此时，企业可增加对年轻人的雇佣，平衡其薪酬支付结构，则人均产出增长速度和就业人数将呈现同时增长。

情形4（图2右）：年龄—劳动生产率曲线呈“倒U”形状，峰值在退休前

此情形下，延迟退休对就业和经济增长的影响将由γR和(γR-ωR)共同决定。若γR＞0和(γR-ωR)＞0，延迟退休将冲击年轻人就业，但有助于提高人均产出的增长速度；若γR＞0和(γR-ωR)＜0，企业将增加对新成长劳动力的雇佣，平衡其薪酬支付结构，才能有效维持合理的平均劳动生产率水平和人均产出增长速度；若γR＜0和(γR-ωR)＜0，延迟退休不仅会降低劳动者的平均劳动生产率，还会增加企业对老年人的薪酬支付负担，最终使得企业陷入发展困境。

2 实证分析

2.1 数据及描述性统计

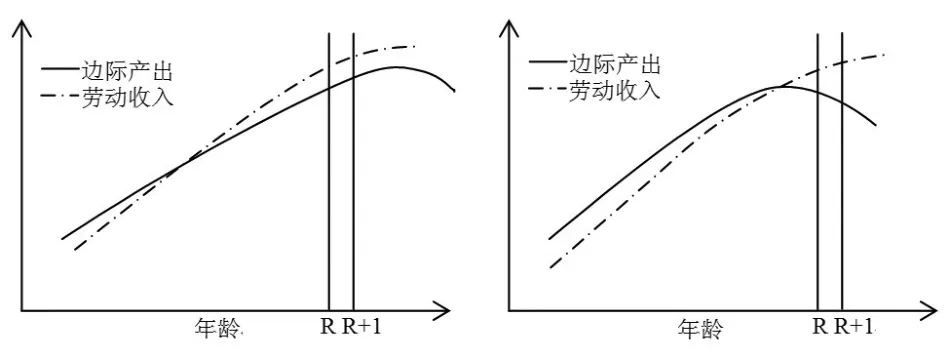
图2 按资分配时年龄—劳动生产率、劳动收入曲线典型形状

为了有效评估年龄—劳动生产率曲线和年龄—劳动收入曲线之间的关系，西方学者一般采用企业微观调查数据。由于缺乏我国的企业微观调查数据，本文选择我国宏观经济和人口数据做近似研究，相关数据全部由历年《中国统计年鉴》整理而得。

（1）产出指标（Q）。选择我国1987—2016年GDP数据，并根据GDP平减指数调整为以1985年价格核算的实际数据。

（3）资本投入指标（K）。在估计资本存量时，学术界一般采用Goldsmith(1951)[8]开创的永续盘存法，计算公式为：

其中，I表示固定资产投资，δ为存量资本的综合折旧率，P为固定资产投资价格指数。《中国统计年鉴》从1990年开始公布固定资产投资价格指数，本文采用工业生产者出厂价格指数作为自变量对1980—1989年间的固定资产投资价格指数进行估算。参照王小鲁等（2000）[9]和郭玉清（2006）[10]的研究成果，折旧率δ取值5%。本文借鉴郭玉清（2006）[10]的研究成果，将我国1980年的资本存量确定为5307.97亿元（按1985年价格核算为6207.3亿元），进而可以推算出历年的资本存量，见表1。

（4）劳动力投入指标（L）。劳动力投入，一般指生产经营活动中实际投入的劳动量。学术界在研究生产函数时，一般选用就业人口数衡量劳动力投入，如郭玉清（2006）[10]、王金营和戈艳霞（2012）[11]等。由于《中国统计年鉴》和《中国人口和就业统计年鉴》等资料中都没有提供就业人口的年龄结构数据，本文选择我国1987年以来15～59岁的5岁间隔细分人口数据作为替代变量。其中，L15、L20、L25、L30、L35、L40、L45、L50和L55分别表示15～19岁、20～24岁、25～29岁、30～34岁、35～39岁、40～44岁、45～49岁、50～54岁和55～59岁人口数。由图3可知，我国劳动力人口平均年龄呈显著上升趋势，1987—2016年间，20～29岁人口占比下降2.3个百分点，30～39岁人口占比下降0.57个百分点，而40～49岁人口占比却上升7.89个百分点，50～59岁人口占比上升5.56个百分点。

2.2 产出模型估计

对于产出模型（4），采用OLS估计，结果见表2。可见，调整后R2为0.999，F统计量为5063.157，回归模型整体上是显著的；稳健标准误对应的t统计量显示，在5%显著性水平下，选择的劳动力人口结构变量对人均产出都有显著影响。由于本文选择劳动年龄人口作为劳动力人口的替代变量，使得劳动力人口占总人口比重对数的系数估计值将是α的有偏估计。郭庆旺和贾俊雪（2005）[12]、郭玉清（2006）[10]等学者都认为我国经济基本上是规模报酬不变的，则本文根据人均资本投入对数的系数估计值推算出α^约为0.484。将各劳动力年龄结构变量的回归系数除以0.484，即可计算20～24岁、25～29岁、30～34岁、35～39岁、40～44岁、45～49岁、50～54岁和55～59岁人口相对于15～19岁人口的边际产出（γj+1），分别为13.02、5.78、14.37、12.36、15.67、8.75、13.43和8.32。可见，我国年龄—劳动生产率曲线总体上呈“倒U”形状，峰值出现在40～44岁，50～54岁人口也有较高的边际产出水平（见图4）。我国总人口中40～44岁人口占比从2007年开始下降，从2007年的9.75%逐渐下降到2016年的8.18%。与此同时，我国GDP增速也从2007年的最高值14.2%逐渐下降到2016年的6.7%。可见，我国主要年龄段劳动力人口规模下降，是我国近几年经济增速下滑的主要原因之一。此外，由于55～59岁劳动者的边际产出水平较低，则延迟退休将降低当前就业者的平均劳动生产率。

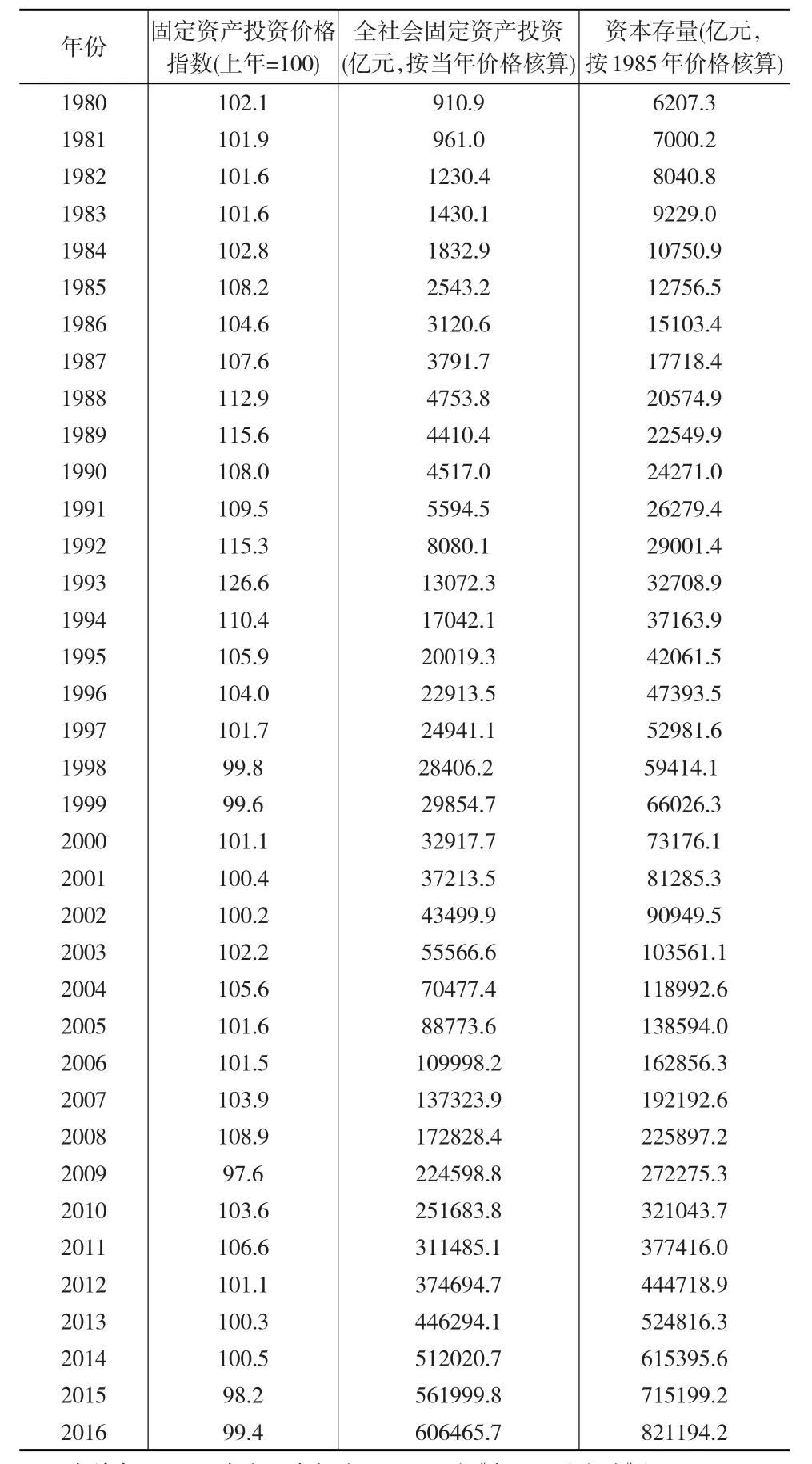
表1 1980—2016年资本存量估算

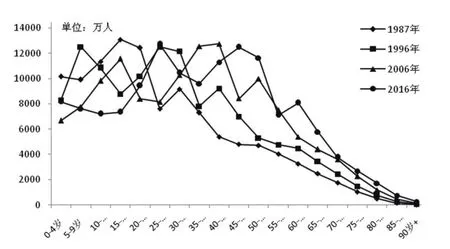
图3 主要年份我国5岁间隔细分人口数

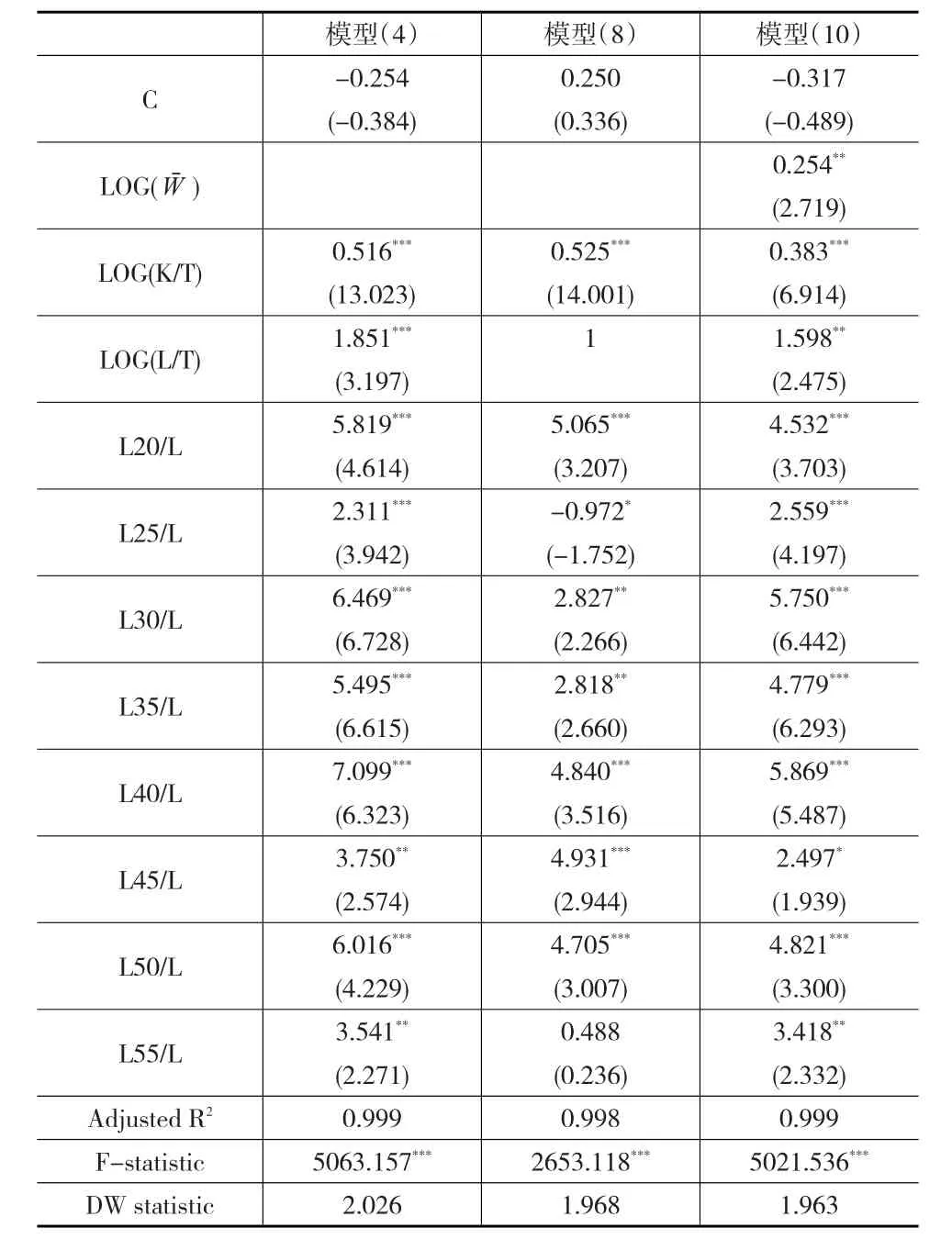
表2 模型估计结果（1）

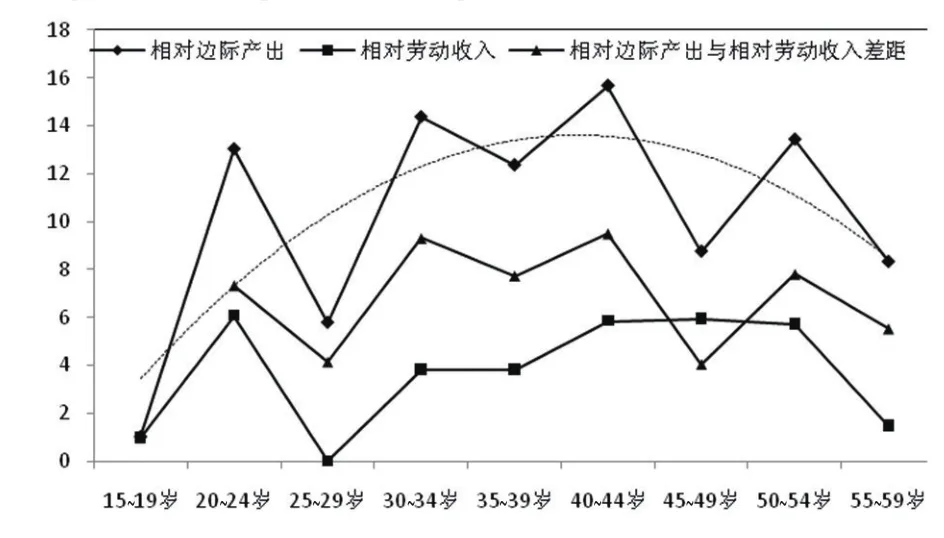
图4 我国劳动力人口的相对边际产出和相对劳动收入

2.3 收入决定模型

对于收入决定模型（8），在按劳分配模式下，无需对回归系数ωj作任何限制，将人均资本投入作为控制变量加入模型，并将劳动力人口占总人口比重对数的系数控制为1，OLS估计结果见表2。可见，被解释变量的总离差有99.8%由回归模型做出解释；t统计量显示，在5%显著性水平下，20～24岁、30～34岁、35～39岁、40～44岁、45～49岁及50～54岁人口相对于15～19岁人口的劳动收入(ωj+1)有明显差别，相对劳动收入分别为6.07、3.83、3.82、5.84、5.93和5.71；25～29岁和55～59岁人口相对于15～19岁人口的劳动收入差别不明显。

在按资分配模式下，分别假定回归系数ωj为工龄①的线性函数、指数函数和二次函数，采用OLS估计，估计结果见表3。相对于表2的估计结果，ωj受约束回归模型的调整后R2较低，AIC和SC值较高，DW统计量显示模型存在自相关问题。综合比较表2和表3的估计结果，本文认为ωj无约束的回归结果更能有效反映人均劳动收入与劳动力人口结构变量之间的关系，各年龄段劳动力人口的相对劳动收入与相对边际产出之间相关程度高于相对劳动收入与年龄之间相关程度，基本支撑我国以按劳分配为主体的收入分配制度。

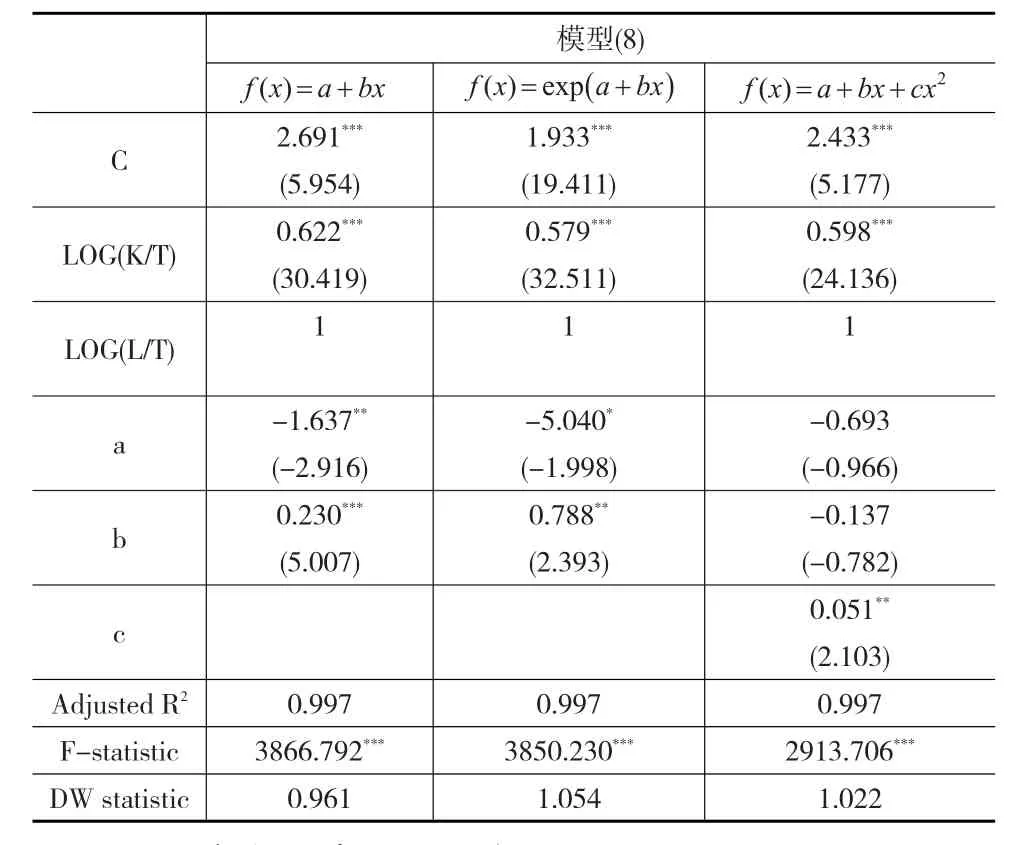
表3 模型估计结果（2）

2.4 边际产出—劳动收入差距模型

对于边际产出—劳动收入差距模型（10），选取劳动力人口占比的对数序列作为控制变量，OLS估计结果见上文表2。可见，模型拟合程度较高，被解释变量的总离差有99.9%可由回归模型做出解释；稳健标准误对应的t统计量显示，在5%显著性水平下，劳动力人口结构变量的回归系数都显著大于0，则认为各年龄段劳动力人口的相对边际产出明显大于相对劳动收入。可见，我国同样存在“productivity-wage gap”现象，相对边际产出与相对劳动收入的差值随年龄增长而变化的曲线呈“倒U”形状，20～24岁、25～29岁、30～34岁、35～39岁、40～44岁、45～49岁、50～54岁和55～59岁年龄段对应的差值分别为7.34、4.14、9.31、7.74、9.5、4.04、7.81和5.53（见图4），峰值同样出现在40～44岁，与模型（4）和模型（8）系数估计值的差值基本相符，相关系数达到了0.92，进一步证实模型构建的合理性。我国劳动力人口的边际产出整体上大于劳动收入，即存在“人口红利”现象，这也是我国近30年保持较快经济增长速度的主要原因。

可见，延迟退休年龄将如何影响我国的经济增长和就业，关键取决于60～64岁人口相对于新成长劳动力的边际产出和劳动收入水平。根据模型（4）和模型（10）的估计结果，构建相对边际产出、相对边际产出与相对劳动收入差值关于工龄的半对数回归模型，估计结果见表4。工龄平方项在5%显著性水平下都是显著的，而且系数为负，进一步证实边际产出、相对边际产出与相对劳动收入差值的年龄曲线呈“倒U”形状，并可预测出60～64岁人口的相对边际产出为3.909，相对边际产出与相对劳动收入的差值为2.708。可见，60～64岁人口的边际产出水平仅高于15～19岁年龄组。

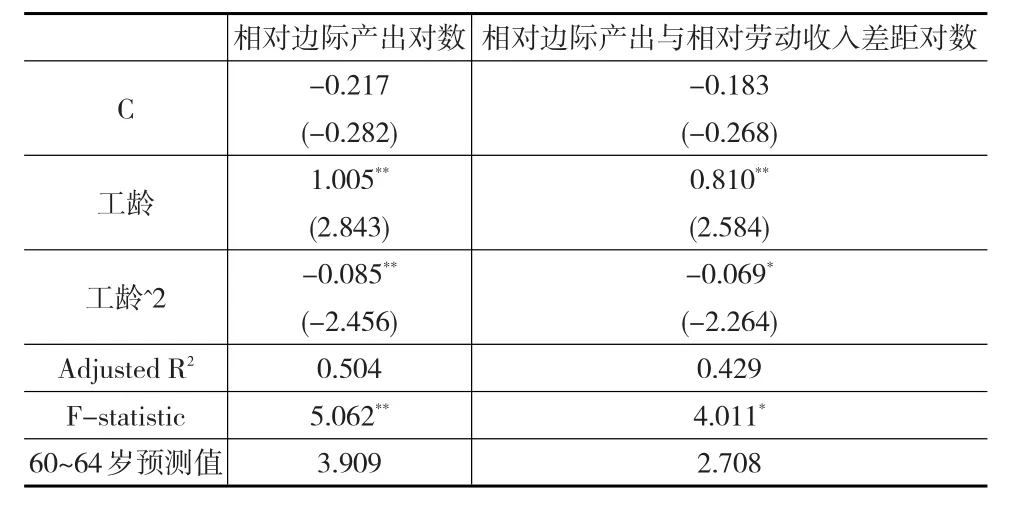
表4 60～64岁人口相对边际产出及相对劳动收入预测

因此，若近阶段实施延迟退休年龄政策，将直接增加劳动力供给，这对经济的影响主要体现在两个方面：一是有利于企业维持目前边际产出与劳动收入的差值(γ-ω)，进而缓解经济下行压力；二是形成老年雇员与新成长劳动力的替代效应。目前，我国的新成长劳动力主要集中在15～24岁年龄段，包括未能继续升学的初、高中毕业生及全日制大中专院校毕业生。60～64岁人口的边际产出高于15～19岁年龄组，但低于20～24岁年龄组。企业增加对20～24岁新增劳动力的雇佣，有助于提高平均边际产出水平。因此，延迟退休有助于提高人均产出的增长速度，但将冲击15～19岁新增劳动力的就业，对20～24岁新增劳动力的就业影响较小。

3 结论

通过实证研究，本文认为我国年龄—劳动生产率曲线总体上呈“倒U”形状；相对于15～19岁年龄组，各年龄段劳动者的相对边际产出显著大于相对劳动收入，不存在对老年雇员的过度支付现象。因此，实证结果一定程度上解释了我国近30年经济高增长和近10年经济增速下滑现象。在此背景下，实施延迟退休年龄政策，将有助于提高人均产出的增长速度，但也会冲击15～19岁新增劳动力的就业，对20～24岁新增劳动力的就业影响较小。

由于60～64岁老年人的劳动生产率水平较低，该人群一旦失业，很难在短时间内获得新的就业机会，即再就业成本较高。因此，出台延迟退休年龄政策，还须进一步完善老年人的就业保障，不仅要加强对临近退休人员的法律保护，还要加大对临近退休前失业人员的财政补贴力度。

此外，我国目前每年新增15～19岁城镇劳动力约750万（主要包括职业学校毕业生、初高中后不再继续升学的），该人群劳动生产率水平最低。政府应加大对该人群的职业技能培训，提高他们的劳动生产率水平。此时，实施延迟退休年龄政策，将在提高人均产出增长速度的同时，还有助于提高新成长劳动力的就业水平。

[1] 陈春，杨琴，杨洁.谈我国退休制度的改革[J].中国劳动，2013，(8).

[2] 王晓军，赵明.寿命延长与延迟退休：国际比较与我国实证[J].数量经济技术经济研究，2015，(3).

[3] 张晓青.人口年龄结构对区域经济增长的影响研究[J].中国人口·资源与环境，2009，(5).

[4] 魏下海，董志强，赵秋运.人口年龄结构变化与劳动收入份额：理论与经验研究[J].南开经济研究，2012，(2).

[5] 徐升艳，周密.东中西地区城市不同年龄组劳动生产率的比较研究[J].上海经济研究，2013，(3).

[6] Stoeldraijer L.Age,Wage and Productivity[R].IZA DP No.4765,Feb⁃ruary 2010.

[7] Mahlberg B,Freund I,Cuaresma J C.Ageing,Productivity and Wages in Austria[J].Labour Economics,2013,(22).

[8] Goldsmith R W.A Perpetual Inventory of National Wealth[J].Nber Chapters,1951,(12).

[9] 王小鲁，樊纲等.中国经济增长的可持续性——跨世纪的回顾与展望[M].北京：经济科学出版社，2000.

[10] 郭玉清.资本积累、技术变迁与总量生产函数——基于中国1980—2005年经验数据的分析[J].南开经济研究，2006，(3).