三峡水库汛末蓄水对鄱阳湖水位的影响研究
2018-03-21刘章君成静清温天福赵楠芳
刘章君,成静清,温天福,牛 娇,赵楠芳
(1. 江西省水利科学研究院,南昌 330029; 2. 水利部鄱阳湖水资源水生态环境研究中心,南昌 330029; 3. 江西省鄱阳湖水资源与环境重点实验室,南昌 330029)
鄱阳湖是中国第1大淡水湖,位于江西省北部、长江中下游南岸,承纳赣江、抚河、信江、饶河、修水等5大河(以下简称“5河”)之来水,经湖盆调蓄后,通过入江水道在湖口注入长江,是一个过水性、吞吐性和季节性湖泊。鄱阳湖水系流域面积16.22 万km2,约占江西省版图面积的97%,占长江流域面积的9%;流域年降水量约1 645 mm,经湖口站出湖入江的多年平均水量为1 436 亿m3,入江水量占长江年径流量的15.5%[1]。鄱阳湖在维护生物多样性、调节长江水量和蓄洪等方面具有重要的作用[2]。
鄱阳湖水位是综合反映湖区水文情势的重要指标。三峡水库建成运行后,汛末蓄水改变了长江中下游的水文过程,对鄱阳湖水位存在潜在影响[3,4]。因此,亟待开展三峡水库汛末蓄水对鄱阳湖水位影响研究。汪迎春等[5]运用长江中游江湖耦合水动力模型的计算结果表明减泄流量1 000~7 653 m3/s使得鄱阳湖湖口、星子和都昌站水位分别降低0.11~1.55、0.10~1.32和0.09~1.11 m,康山站水位变化很小,对鄱阳湖水位影响呈现北高南低的格局。董增川等[6]通过建立反映水文情势变化的人工神经网络模型,根据大通站丰、平、枯典型年模拟三峡水库10月份减少泄流对星子站水位的影响,模拟结果表明水位最大降幅为1.41~2.12 m,平均降幅为0.67~1.12 m。方春明等[7]通过机理研究发现三峡水库运用30 a后,在河道冲刷、鄱阳湖可补水量减小和三峡蓄水的共同作用下,蓄水期湖口站水位下降将为2.00 m左右,相当于把鄱阳湖的枯水季节提前了接近1个月。赖锡军等[8]运用长江中游江湖耦合水动力学模型,以2006年三峡蓄水试验为例,结果表明受蓄水影响鄱阳湖湖口、星子、都昌和康山站水位平均下降0.94、0.74、0.50和0.03 m,水位影响格局呈北高南低。许继军和陈进[9]选取典型水文年,在演算分析基础上认为三峡水库汛末蓄水将降低湖口水位0.40~1.60 m,导致湖区水位相应下降0.30~1.20 m。张奇等[10]采用水动力模拟和湖泊水量平衡方法就鄱阳湖近10 a多来的低枯水位发生机制开展深入研究,结果发现相对于鄱阳湖流域气候变化的影响,长江来水减少是造成湖泊秋季异常低水位的主要因素,长江的拉空作用甚至可以波及至湖泊上游约100 km湖面。这些研究对深入认识和理解三峡水库对鄱阳湖水位的影响作用机制及定量评价其影响程度具有重要参考价值。
以上研究大多采用较为复杂的水文-水动力耦合模型进行分析计算,但是该类方法往往需要大量的水文、气象、地理地貌、工程布局及运行等信息,当资料条件难以满足时将限制其实际应用。为此,一些基于宏观因果关系的系统分析方法,如神经网络模型、多元回归模型、线性动态系统模型等,因其对资料条件要求相对较低,在水文实际应用中也发挥着重要作用[11]。因此,本文将采用多元线性回归模型定量评价三峡水库蓄水对鄱阳湖水位的影响。首先,对蓄水期长江汉口平均流量和5河平均入流量进行独立性检验;然后,采用多元线性回归模型建立鄱阳湖水位与汉口平均流量、5河平均流量的函数关系,并假设该函数关系在三峡水库运行前后保持不变;最后,通过分析三峡蓄水后长江汉口平均流量的改变量,进而得出鄱阳湖水位的变化。
1 研究数据
1.1 基本数据
本文使用的基本资料为1953-2007年的日资料,包括长江水情代表站汉口站流量;鄱阳湖5河入湖流量,由赣江外洲站、抚河李家渡站、信江梅港站、饶河(乐安河)虎山站、饶河(昌江)渡峰坑站、修水万家埠站和虬津站的流量相加得到;鄱阳湖湖区星子站、都昌站和康山站的水位。
1.2 蓄水方案拟定
三峡水库是目前世界上最大的水电站,坝址位于湖北省宜昌市上游40 km处的三斗坪。控制流域面积100 万km2,多年平均年径流量4 510 亿m3。设计正常蓄水位175 m,总库容393 亿m3,防洪库容221.5 亿m3。它是综合治理长江中下游防洪问题的一项关键性措施,并兼有发电、航运和发展库区经济等巨大效益。
按照三峡水库的调度运行方式,每年汛末水库开始蓄水,水库水位从145 m蓄至175 m,与天然入流相比,减少下泄流量,将会影响鄱阳湖湖区的水位。不同的蓄水方案,由于蓄水时段的不同,相应减少的下泄流量也有所变化,对鄱阳湖水位的影响程度也不同。因此,为了比较不同蓄水方案对鄱阳湖水位的影响,本文拟定了三峡水库3种蓄水方案进行分析。其中,方案1为原设计方案,方案2为2009年水利部批准的优化方案,方案3为文献[12]推荐的最优提前蓄水方案。各方案的蓄水起止日期、蓄水天数和平均减泄流量分别见表1。
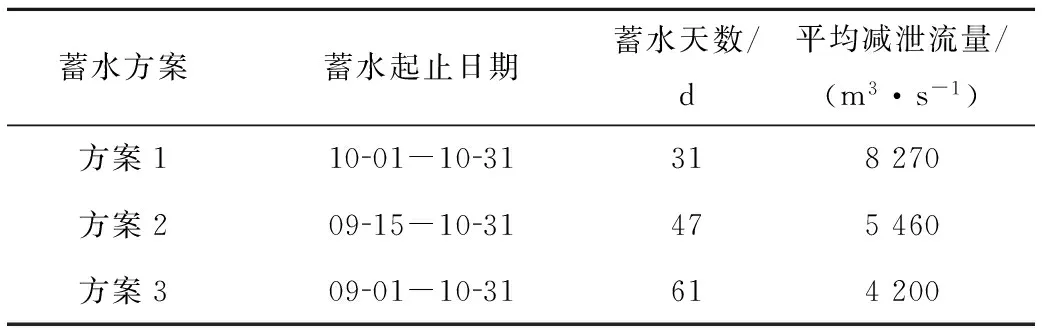
表1 三峡水库3种蓄水方案及平均减泄流量Tab.1 Three impoundment schemes of Three Gorges Reservoirand average reduced discharge
1.3 取样方法
汉口平均流量、5河平均流量和湖区星子站、都昌站和康山站平均水位系列通过考虑水流传播时间的相应取样方式确定。三峡水库蓄水期间长江宜昌至湖口站间水流传播时间的确定参考文献[13]的研究成果。以蓄水方案1为例,根据蓄水起止日期10月1日至10月31日,将时间向后推5 d(水流从三峡水库坝址至汉口的平均传播时间),选取对应10月6日至11月5日期间内汉口的平均流量,再将时间向后推4 d(水流从汉口至鄱阳湖湖口的平均传播时间),选取对应10月10日至11月9日期间内5河的平均流量和湖区星子站、都昌站和康山站的平均水位,这样就构成蓄水方案1的汉口平均流量系列、5河平均流量系列和湖区星子站、都昌站和康山站平均水位系列。其他蓄水方案下的汉口平均流量系列、5河平均流量系列和湖区星子站、都昌站和康山站平均水位系列也采用同样的方法得到。
2 研究方法
2.1 独立性检验
衡量变量之间相关程度的强弱,并用适当的统计指标表示出来,这个过程就是相关分析。常用的相关系数主要有Pearson线性相关系数r、Kendall秩相关系数τ和Spearman秩相关系数ρs[14]。一般来说,如果2个随机变量的相关性越高,则相关系数的绝对值会越大;反之,则相关系数的绝对值越小。但是,有时即使2个随机变量的不相关,甚至相互独立,由于抽样的随机性仍有可能有较大的样本相关系数。因此,有必要对相关系数ρ是否显著进行检验。
提出原假设:
H0:ρ=0,H1:ρ≠0
采用统计量t进行显著性检验,计算公式如下[15]:
(1)
式中:n为样本数。
当统计量 的显著性概率p<0.05时,拒绝原假设,说明2个变量间相关性显著,相关系数不为零;否则,接受原假设,说明2个变量的相关系数为零。在工程实际中通常认为这2个变量是相互独立的。
2.2 多元线性回归
在实际问题中,因变量的变化往往受几个重要因素的影响,此时就需要用2个或2个以上的影响因素作为自变量来解释因变量的变化,这就是多元回归。当多个自变量与因变量之间是线性关系时,所进行的回归分析就是多元线性回归。
设y为因变量,x1,x2,…,xk为自变量,并且自变量与因变量之间为线性关系时,则多元线性回归方程为:
y=b0+b1x1+b2x2+…+b2xk
(2)
式中:b0为常数项;bi(i=1,2,…,k)为偏回归系数。
在进行多元线性回归时,一般要求各自变量之间是相互独立的。在求出回归方程后,必须进行统计检验,才能确定回归方程是否有效。采用确定性系数R2作为检验多元线性回归方程与样本值拟合优度的指标,R2越接近于1,表示回归方程与样本拟合的越好;反之,回归方程与样本值拟合较差。利用F检验法检验回归方程的显著性,当统计量F的显著性概率p<0.05时,认为多元线性回归方程是显著的,自变量和因变量在总体上存在显著的线性关系。利用t检验法检验回归方程中各个偏回归系数的显著性,当统计量t的显著性概率p<0.05时,认为此自变量对因变量的作用是显著的。
多元线性回归方程中,由于各自变量的单位和波动程度可能不同,其偏回归系数之间是无法直接比较的。需要对偏回归系数进行标准化,以消除量纲和波动程度的影响。标准化的偏回归系数的计算公式为[16]:
(3)
式中:σXi、σY分别为自变量Xi和Y的标准差;βi绝对值的大小,可以用来说明各自变量在多元回归方程中的相对重要性,即衡量自变量对因变量贡献的大小。
3 结果与分析
3.1 汉口流量和5河入流的独立性检验
在建立多元线性回归方程之前,先对汉口流量和5河入流量进行独立性检验。采用1953-2002年的资料点绘了3种蓄水方案下汉口流量和5河入流的相关图,见图1。可以看出,散点均匀的散布在二维空间区域,表明汉口流量和5河入流相关性不高。

图1 汉口流量和五河入流相关图Fig.1 Scatter diagram of Hankou flow and catchment inflow
为了定量分析汉口流量和5河入流之间的相关程度,计算了2者的Pearson线性相关系数r、Kendall秩相关系数τ和Spearman秩相关系数ρs,结果见表2。可以发现,3种蓄水方案下统计量 的显著性概率p>0.05,接受原假设,说明2个变量的相关系数为零,在工程实际中可以认为这2个变量是相互独立的。因此,满足了多元线性回归模型中的各自变量相互独立这一基本要求。
3.2 鄱阳湖水位函数的建立
采用多元线性回归模型分别建立鄱阳湖湖区星子站、都昌站和康山站水位与汉口平均流量、5河平均流量的函数关系。式(2)可具体表达为:
y=b0+b1x1+b2x2
(4)
式中:y为鄱阳湖湖区水位;x1、x2分别为汉口平均流量和5河平均流量。

表2 3种相关系数及统计检验结果Tab.2 Three correlation coefficients and statistical test results
将1953-2007年资料分为蓄水前的率定期(1953-2002年)和蓄水后的检验期(2003-2007年)。采用率定期的资料系列,利用统计软件SPSS 19.0计算各回归方程的偏回归系数bi、标准化的偏回归系数βi和确定性系数R2,结果见表3。F检验和t检验的统计量值及相应的显著性概率p,结果分别列于表4和表5。
由表3可以发现,3种蓄水方案下星子站、都昌站和康山站水位回归方程的确定性系数R2均较高(0.831~0.917),表明多元回归方程与样本的拟合效果较好。时间上,从蓄水方案1到方案3,起蓄时间提前,确定性系数R2增加;空间上,从星子站到康山站,由北向南距离湖口越来越远,确定性系数R2也增加。表4的结果显示,3种蓄水方案下统计量F的显著性概率p<0.05,说明多元线性回归方程是显著的,即鄱阳湖水位与汉口平均流量、5河平均流量在总体上存在显著的线性关系。表5中各个偏回归系数的统计量t显著性概率p<0.05,进一步表明汉口平均流量、5河平均流量对鄱阳湖水位的作用均是显著的。
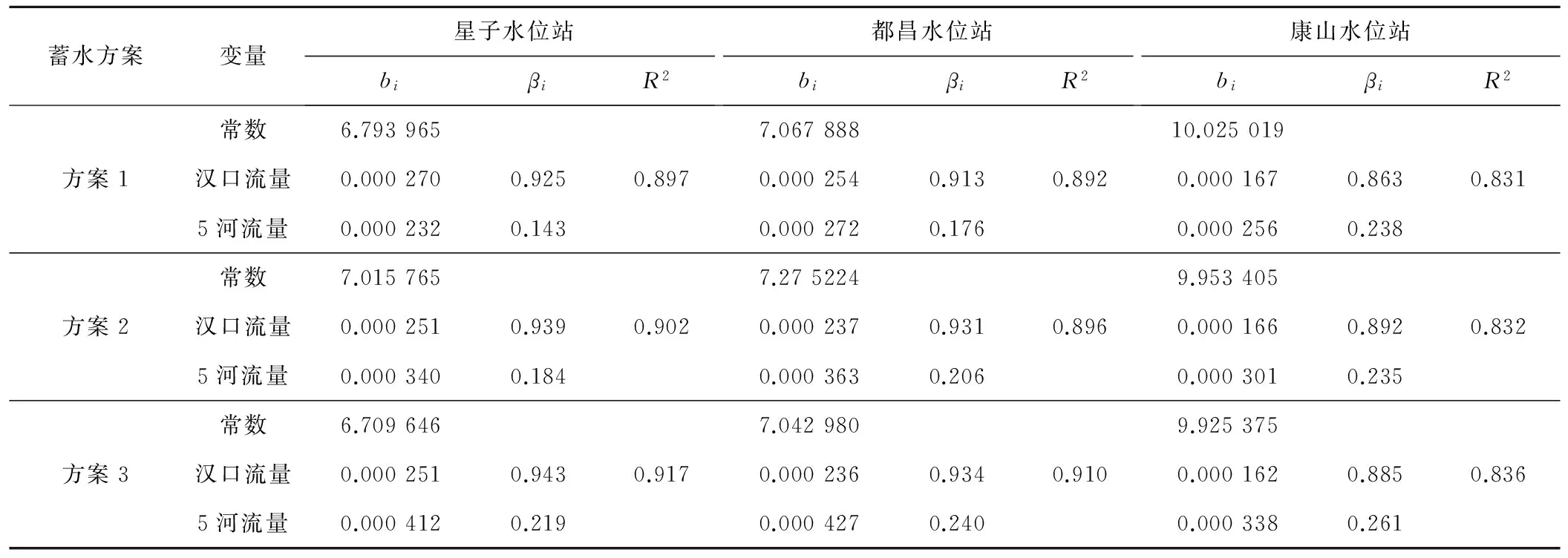
表3 多元线性回归方程参数估计结果Tab.3 Parameter estimation results of multiple linear regression equation

表4 多元线性回归方程的F检验结果Tab.4 F test results of multiple linear regression equation
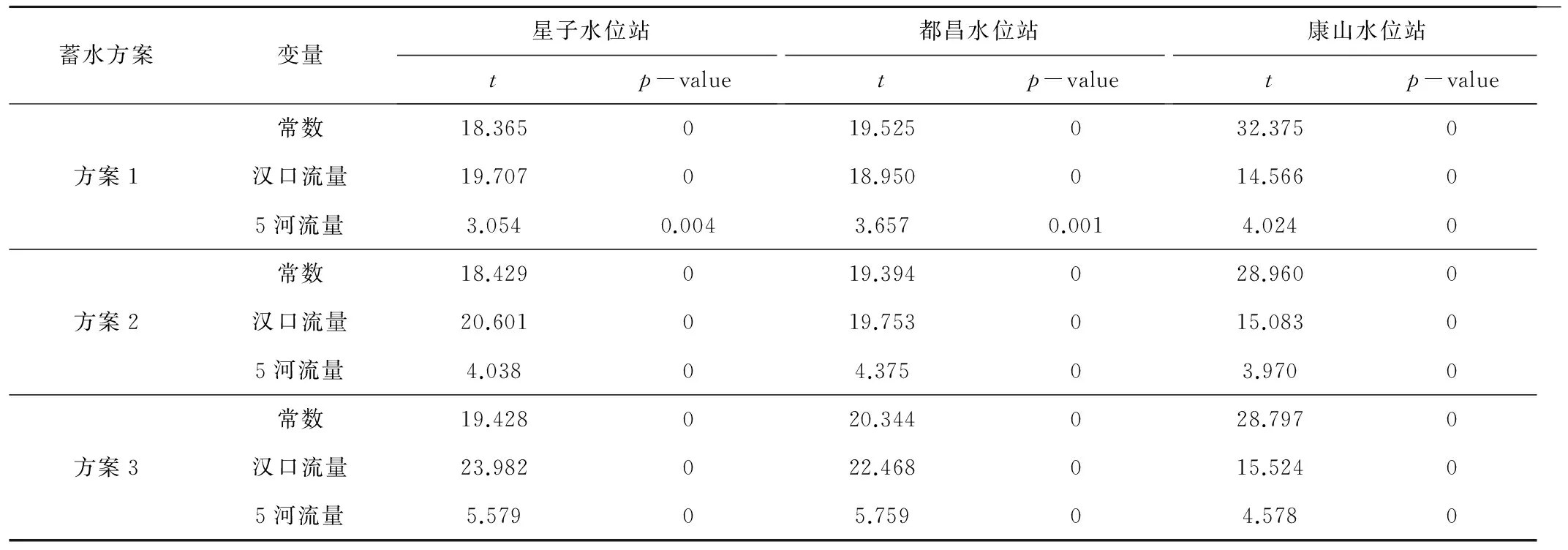
表5 偏回归系数的t检验结果Tab.5 t test results of partial regression coefficent
图2给出了率定期和检验期的星子站、都昌站和康山站多元线性回归水位模拟结果和实测值对比图。可以看出,模拟值和实测值总体上拟合效果均较好,且拟合效果随着起蓄时间的提前,星子站到康山站逐步提高。率定期和检验期多元线性回归模型的平均相对误差绝对值统计见表6。率定期星子站、都昌站和康山站的平均误差分别为2.34%~3.01%、2.28%~2.70%
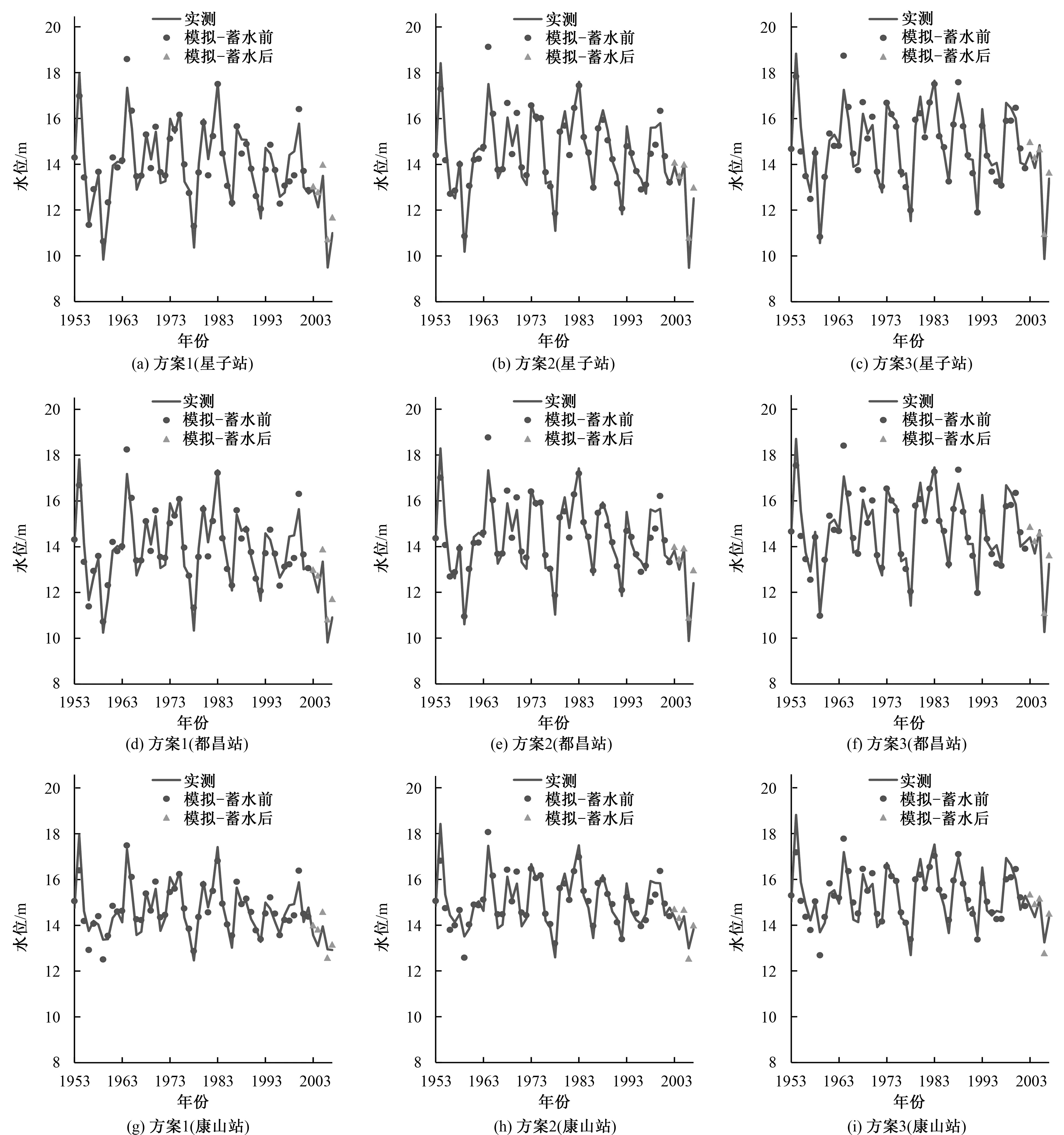
图2 多元线性回归水位模拟结果和实测值对比Fig.2 Comparison of observed and simulated water levels by multiple linear regression model
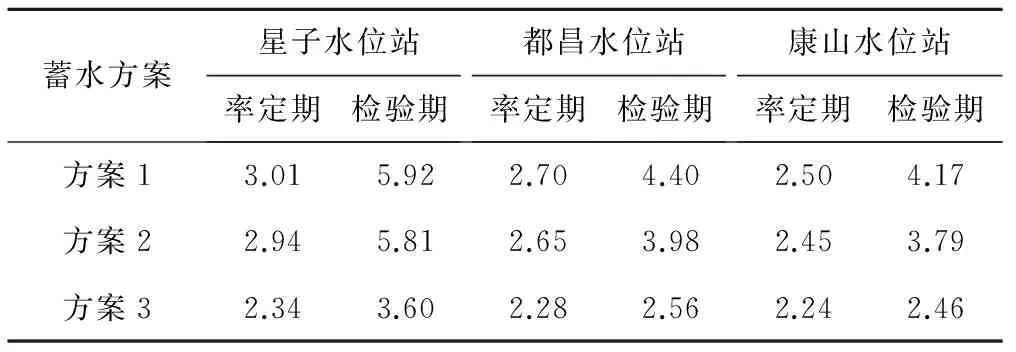
和2.24%~2.50%,检验期分别为3.60%~5.92%、2.56%~4.40%和2.46%~4.17%。可知,率定期和检验期多元线性回归模型的精度均较高,表明假设鄱阳湖水位函数关系在三峡水库运行前后保持不变具有一定的合理性。
以上结果和分析表明采用本文建立的多元线性回归模型来预测三峡水库运行后的鄱阳湖星子站、都昌站和康山站的水位,进而定量评价三峡水库蓄水对鄱阳湖区水位的影响是合理可行的。从表3标准化的偏回归系数结果可以发现,汉口流量对鄱阳湖水位的贡献比5河入流要大,即说明汉口流量在多元回归方程中相对更重要。从长江-鄱阳湖-5河系统的相互关系上看,三峡水库蓄水期间长江水情对鄱阳湖水位具有主导地位。相对于鄱阳湖流域气候变化引起的5河流量减小,长江对鄱阳湖的拉空作用比人们想象的要大,长江来水减少是造成鄱阳湖秋季异常低水位的主要因素,这与文献[10]采用水文-水动力耦合模型的研究结果是一致的。
3.3 蓄水对鄱阳湖水位的影响分析
对式(4)求微分可得:
Δy=b1Δx1+b2Δx2
(5)
式中:Δy为鄱阳湖水位变化量;Δx1、Δx2分别为汉口流量和5河流量的变化量。
在评价三峡水库汛末蓄水的影响分量时,假设5河平均流量不变,即式(5)中Δx2=0,因此有Δy=b1Δx1,表明三峡水库蓄水对鄱阳湖水位的影响是通过改变长江水情而起作用的。通过分析三峡蓄水后长江汉口平均流量的改变量Δx1,进而得出鄱阳湖水位的变化。根据表1给出的3种蓄水方案下星子站、都昌站和康山站的平均减泄流量值Δx1(假定三峡水库减泄的那部分流量,不会在中途减少或增加)和表3中相应的汉口流量偏回归系数b1就可以求出对应的鄱阳湖区水位变化量Δy,结果见表7。
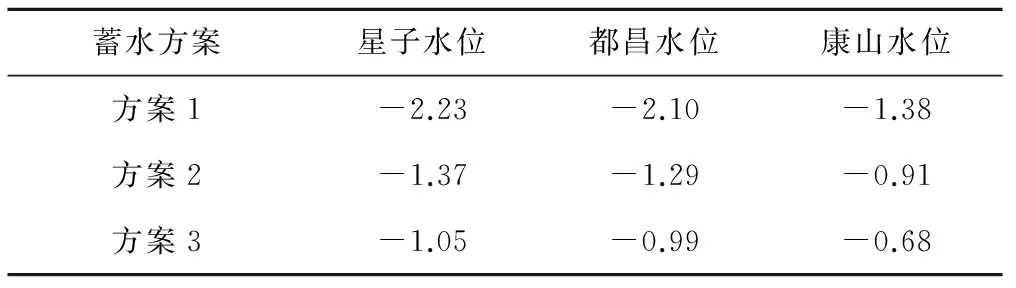
表7 三峡水库不同蓄水方案下鄱阳湖湖区水位变化量 m
注:表中水位变化量为负数表示水位降低。
由表7可以发现,三峡水库运行后鄱阳湖湖区的水位都将有所降低,且不同蓄水方案降低幅度不同:从方案1到方案3,蓄水天数逐渐延长,减泄流量减少,所以鄱阳湖湖区的水位的降低幅度也在减小。以星子站为例,方案1、2和3对应的水位降低值分别为2.23、1.37和1.05 m。此外,从星子站到康山站,由于距离湖口越来越远,受长江水情的影响程度逐渐减弱,水位的降低幅度也在减小,蓄水影响呈北高南低的空间格局。按2009年水利部批准的优化方案(方案2),星子站、都昌站和康山站的水位降低值分别为1.37、1.29和0.91 m。
4 讨 论
三峡水库汛末蓄水将降低鄱阳湖湖区水位,对湖区生态环境及湖区生产、生活用水产生较大的不利影响。针对这些影响,本文从优化三峡水库和鄱阳湖5河支流水库的运行调度等方面提出一些保护对策与措施,供鄱阳湖的综合开发治理参考。
4.1 优化三峡水库汛末蓄水调度
由上述分析可知,长江水情对鄱阳湖水位具有主导地位,长江来水减少是造成鄱阳湖秋季异常低水位的主要因素,可以预见这种影响将随着长江上游干支流大量水库群的投入运行变得更加严重[10]。因此,需要优化三峡水库汛末蓄水调度,科学把握三峡水库汛末蓄水时机,慎重地综合考虑蓄水期间三峡水库上游来流、5河入流以及湖区退水过程等水情预报因素,适当调整三峡水库蓄水进程。可以考虑将三峡水库汛末蓄水时间适当提前,尽量减轻水库减泄流量过程对鄱阳湖水位变化的干扰,避免出现极端的枯水水情。从本文计算结果来看,三峡水库汛末蓄水时间10月1日、9月15日和9月1日对应的星子站水位降低值分别为2.23、1.37和1.05 m,都昌站分别为2.10、1.29和0.99 m,康山站分别为1.38、0.91和0.68 m。可以发现,适当提前三峡水库汛末蓄水时间对减轻鄱阳湖不利影响效果显著。按2009年水利部批准的优化方案,目前起蓄时间已经优化调整到9月15日,但能否继续提前需要进一步的分析论证。
4.2 加强鄱阳湖5河支流蓄水工程的调度
5河入湖流量对鄱阳湖水位的变化也有重要的作用。从表3中的结果可以得到不同三峡水库蓄水方案下蓄水期间5河入湖流量增加对鄱阳湖水位的影响。以2009年水利部批准的优化方案(方案2)为例,当长江汉口流量不变时,蓄水期间5河入湖流量每增加1 000 m3/s,鄱阳湖星子站、都昌站和康山站的水位分别增加0.340、0.363和0.301 m。加强5河支流蓄水工程调度的主要目的,是想提高5河支流洪水资源利用率,5河支流水库在8-9月份汛期结束之前,适当多拦蓄一些汛末洪水,留存库中,这样在三峡水库蓄水期间,可在一定程度上增加5河入湖流量,弥补和减轻三峡水库减泄的不利影响。
5 结 论
本文在对蓄水期汉口平均流量和5河平均入流进行独立性检验的基础上,分别采用多元线性回归模型建立鄱阳湖星子站、都昌站和康山站平均水位与汉口平均流量、5河平均流量的函数关系,通过拟定3种不同的蓄水方案得到三峡水库蓄水后长江汉口平均流量的变化量,分析了鄱阳湖水位的变化大小和空间格局特征。主要研究结论如下。
(1)蓄水期间汉口平均流量和5河平均流量之间相互独立,鄱阳湖平均水位与2者存在显著的线性关系。利用本文建立的多元线性回归模型来预测三峡水库运行后的鄱阳湖水位,进而定量评价三峡水库蓄水对鄱阳湖区水位的影响是合理可行的。
(2)三峡水库汛末蓄水将降低鄱阳湖湖区的水位,且不同蓄水方案和不同站点的降低幅度不同。起蓄时间10月1日、9月15日和9月1日对应的星子站水位降低值分别为2.23、1.37和1.05 m,都昌站分别为2.10、1.29和0.99 m,康山站分别为1.38、0.91和0.68 m。鄱阳湖水位受三峡蓄水的影响随着起蓄时间的提前而减弱,空间上呈北高南低的格局。
(3)从长江-鄱阳湖-5河系统的相互关系上看,三峡水库蓄水期间长江水情对鄱阳湖水位具有主导地位。相对于鄱阳湖流域气候变化引起的5河流量减小,长江对鄱阳湖的拉空作用比人们想象的要大,长江来水减少是造成鄱阳湖秋季异常低水位的主要因素。
□
[1] 谭国良, 郭生练, 王 俊, 等. 鄱阳湖生态经济区水文水资源演变规律研究[M]. 北京: 中国水利水电出版社, 2013.
[2] Jiao L. Scientists line up against dam that would alter protected wetlands [J]. Science, 2009,326:508-509.
[3] 刘文标. 三峡水库运行初期对鄱阳湖汛期高水位出现时间的影响[J]. 中国农村水利水电, 2014,(12):77-78.
[4] 杨沛钧, 廖智凌. 鄱阳湖流域江湖关系研究综述[J]. 中国农村水利水电, 2017,(3):65-67.
[5] 汪迎春, 赖锡军, 姜加虎, 等. 三峡水库调节典型时段对鄱阳湖湿地水情特征的影响[J]. 湖泊科学, 2011,23(2):191-195.
[6] 董增川, 梁忠民, 李大勇, 等. 三峡工程对鄱阳湖水资源生态效应的影响[J]. 河海大学学报(自然科学版), 2012,40(1):13-18.
[7] 方春明, 曹文洪, 毛继新, 等. 鄱阳湖与长江关系及三峡蓄水的影响[J]. 水利学报, 2012,43(2):174-181.
[8] 赖锡军, 姜加虎, 黄 群. 三峡工程蓄水对鄱阳湖水情的影响格局及作用机制分析[J]. 水力发电学报, 2012,31(6):132-136.
[9] 许继军, 陈 进. 三峡水库运行对鄱阳湖影响及对策研究[J]. 水利学报, 2013,44(7):757-763.
[10] Zhang Q, Ye X, Werner A D, et al. An investigation of enhanced recessions in Poyang Lake: comparison of Yangtze River and local catchment impacts[J]. Journal of Hydrology, 2014,517:425-434.
[11] 梁忠民, 郭 彦, 胡义明, 等. 基于copula函数的三峡水库预泄对鄱阳湖防洪影响分析[J]. 水科学进展, 2012,23(4):485-492.
[12] 李 雨, 郭生练, 郭海晋, 等. 三峡水库提前蓄水的防洪风险与效益分析[J]. 长江科学院院报, 2013,30(1):8-14.
[13] 肖 魁, 陈 进. 长江宜昌-九江站间水流传播时间分析[J]. 中国农村水利水电, 2011,(4):1-5.
[14] Yu K, Xiong L, Gottschalk L. Derivation of low flow distribution functions using copulas [J]. Journal of Hydrology, 2014,508:273-288.
[15] Sun S, Chen H, Ju W, et al. On the attribution of the changing hydrological cycle in Poyang Lake Basin, China [J]. Journal of Hydrology, 2014,514:214-225.
[16] 黄振平. 水文统计学[M]. 南京:河海大学出版社, 2003.
