2参数月水量平衡模型在尼洋河流域的应用研究

张东艳，杨欣玥，侯雨坤

(1. 西藏农牧学院，西藏 林芝 860000；2.河海大学水文与水资源学院，南京 210098；3. 武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

在分析气候变化对水资源的影响方面，传统的随机或统计水文学方法所提供的信息量已不能满足实际需要，因此，流域水文模型作为水文科学中最重要的分支之一，得到了广泛地推广。其中水量平衡模型简单实用，在水利工程规划设计、流域中长期水文模拟、洪水预报、水资源开发利用中已经得到了广泛应用[1]，为解决各种工程水文问题和提高人们对水文规律的认识起到了巨大作用。

目前，国内外水文学者研发了较多的月水量平衡模型[2]，月模型的主要输入为月降雨量和月蒸发量，输出为月径流。月模型主要结合流域土壤中的含水量，以质量守衡原理为理论基础，将各个水文过程或变量之间的关系概化成经验函数或表达式来模拟流域水文过程。相对于对资料要求较高的其他月水量平衡模型，熊立华、郭生练等提出了2参数月水量平衡模型(简称TPWB模型)，在东江、赣江和汉江的70个子流域进行了检验和校核，结果表明模型结构简单，模拟效果较好[3-5]。因此，本文采用2参数月水量平衡模型模拟尼洋河流域自然条件下的径流变量。

1 尼洋河流域背景概况

尼洋河流域位于西藏自治区东南部，东经92°10′～94°35′、北纬29°28′～30°30′，发源于念青唐古拉山南麓工布江达县西部的错水果拉冰川湖，流经工布江达县和林芝县，于林芝县的格则村附近汇入雅鲁藏布江。流域内山峦起伏，山脉纵横交织，形成了许多沟壑谷川，流域平均海拔在4 000 m以上，河谷海拔3 000～3 500 m，最高山峰海拔6 800 m，其中农田主要分布在尼洋河河谷及沿河支沟沟谷内，海拔4 200 m以下一般为森林，4 200～4 500 m为灌丛草甸带，4 500～5 200 m为高山草甸带，5 200 m以上为高山寒冷带和高山冰雪带。

尼洋河流域水系发达，全长307.5 km，流域面积达17 732 km2，其中大于100 km2的1级支流有白曲、娘曲、巴朗曲、巴河和八及曲等19条，尼洋河流域水系见图1。

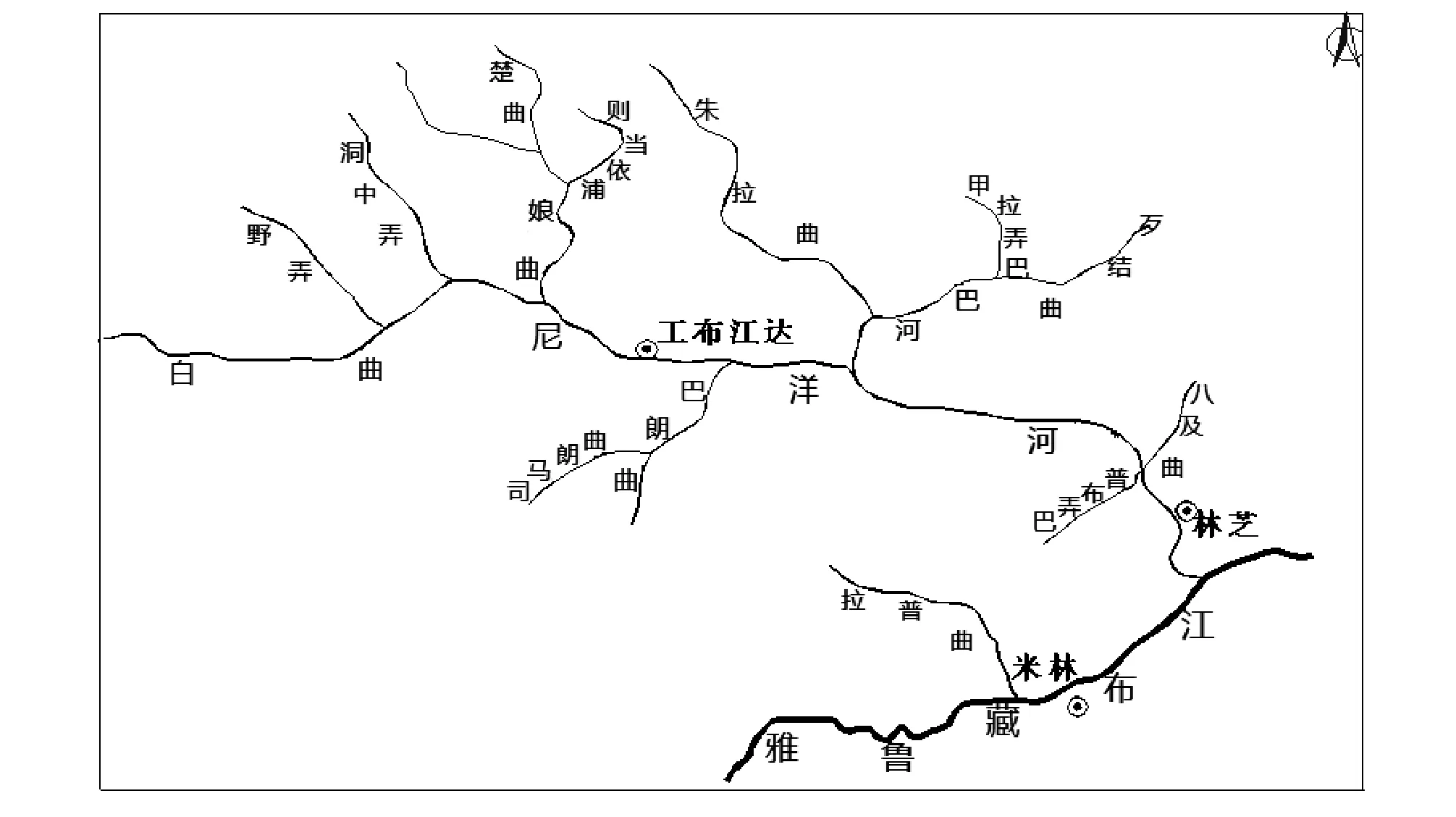
图1 尼洋河流域水系Fig.1 The water system images of Niyanghe basin

尼洋河流域水系发达，支流众多，上游最大支流为娘曲，河长86 km，,中游河段最大支流巴河，河长106 km。尼洋河流域径流补给形式主要有雨水、冰雪融水和地下水3种，其中雨水受到降水、蒸发、气温等气象因素的影响，该流域多年平均降水量为700～1 100 mm，降雨主要集中在6-9月，占全年降雨量的75%以上。冰雪融冰主要集中于尼洋河上游，内冰川及永久性积雪面积975 km2，占流域总面积的5.47%。地下水受到地壳运动的影响，裂隙水和断层水形成的泉水涌水量大。全球气候变化带来的水资源演变规律的异常，增加了尼洋河流域水资源管理的复杂性和不确定性。同时，随着全球气候变暖，将出现更多高温、暴雨洪涝、干旱等极端天气，因此在未来气候变暖背景下极端天气事件对尼洋河流域防灾减灾、经济社会发展的影响亟待进行深入研究。

2 2参数月水量平衡模型结构

2参数月水量平衡模型主要用来模拟和预测不同气候条件下流域上的月径流量，较之日径流过程，月径流过程已经概化掉了存在于较短时间尺度上的一些随机不确定因素，土壤—植被—大气系统(SPAC)之间的相互作用，相互反馈使得月降水、月蒸发，月径流这3个水文变量之间的相关关系更加密切。在自然条件下，假如无明显的蓄水或取水，一次降雨一般都能在1个月内转化为径流或被蒸发，仅有小部分仍滞留在土壤中。因此，在月水量平衡模型中已没有区别产流与汇流的必要，所以模型结构简单，参数较少，便于推广应用。

2.1 模型计算

2.1.1 月实际蒸发量E的计算

现有很多计算流域实际蒸发量的公式，实际应用中主要是根据流域所能提供的资料来选择合适的公式。事实上，水文学家和工程师接触最多，利用最多的蒸发资料通常就是蒸发皿观测值，并用它来近似代替流域的蒸散发能力。如何把蒸发皿观测值转化为实际蒸散发，普遍的做法是乘以一个小于1.0的折减系数，这个系数一般被视为土壤含水量的函数。当流域降水比较丰富时，土壤中湿度比较大，空气湿度也比较大，故实际蒸发值与观测值的反差并不强烈；当流域上降水比较少时，空气中水分不饱和系数比较大，蒸发皿观测值很大，然而同时因土壤湿度也很低，可供蒸发水量少，实际蒸发值很低，如此一来，实际蒸发量与蒸发皿观测值的反差很大。关于降水与蒸发之间的作用与反作用问题，Morton[6]已给出过相当精辟的分析和讨论，在此暂不详述。

Ol'dekop曾于20世纪60年代建议采用下式来计算流域的年实际蒸发量：

E(t)=EP(t) tanh[P(t)/EP(t)]

(1)

式中：E(t)表示年实际蒸发值，mm；EP表示年蒸发皿观测值，mm；P表示年降水量，mm；tanh[P/EP]被看作从蒸发皿观测值到实际蒸发值的转换系数，它是降水量P与蒸发皿观测值EP比值的双曲正切函数，其值上限为1.0。

公式(1)可写成另一种形式：

E(t)/EP(t)=tanh[P(t)/EP(t)]

(2)

式(2)更加清楚地反映出E、EP和P3者之间的内在关系：P/EP的值越大，E就越趋近EP，例如，当P/EP的值等于1.0时，E/EP的值为0.816；当P/EP的值等于2.0时，E/EP的值为0.98。还有一点值得注意，那就是函数tanh(x)是变量x的压缩变换，反映了流域土壤较之空气对水文现象或过程更大的缓冲和调节能力。式(1)乘以一个系数后用来计算月实际蒸发值，以反映降水和蒸发的年内变化规律，即：

E(t)=cEP(t) tanh[P(t)/EP(t)]

(3)

式中：E代表流域月实际蒸发值；EP代表月蒸发皿观测值；P代表月降水量；系数c是本文模型中的第1个参数，综合反映蒸发和降水变化情况。

在实际计算中用蒸发蒸腾量(PET)代替蒸发皿观测值，在PET的计算方面采用世界粮农组织(FAO)推荐的参照蒸发量的标准计算方法彭曼蒙泰斯(Penman-Monteith， P-M)公式：

(4)

式中：PET为潜在蒸散量，mm/d；T为平均气温，℃；Δ为温度～饱和水汽压关系曲线上在T处的切线斜率，kPa/℃；Rn为净辐射，MJ/(m2·d)；G为土壤热通量，MJ/(m2·d)；γ为湿度表常数，kPa/℃；u2为距离地面2 m高处风速，m/s；ea为饱和水汽压，kPa；ed为实际水汽压，kPa。

2.1.2 月径流量Q的计算

月径流量Q与该月土壤中的净含水量S(即扣除了蒸发之后的剩余水量，mm)有着十分密切的关系，S越大，水分流出土壤的可能性越大，则Q越大。如若把整个流域的调蓄作用当作一个“水库”(尽管“水库”中还有土壤和空气)，Q便可简化为S线性或非线性函数，这是一种简单和常用的方法。假定月径流为土壤含水量的双曲正切函数关系：

Q(t)=S(t) tanh[S(t)/SC]

(5)

式中：Q(t)是月累积径流深，mm；S(t)是当月土壤净含水量；SC是本模型中所用的第2个参数，即流域最大蓄水能力。

假设土壤中某时刻的稳定含水量(即扣除了出流Q和蒸发E之后的土壤含水量)与土壤的当时蓄水能力Wm(t)成正比关系，那么Wm(t)的表达式为：

Wm(t)=[S(t)-Q(t)]SC/S(t)=[1.0-Q(t)/S(t)]SC

(6)

把公式(5)代入式(6)可得：

Wm(t)={1.0-tanh[S(t)/SC]}SC

(7)

此时Wm(t)是一个关于S(t)的单调减函数，其最大值为流域最大蓄水能力SC。

2.1.3 模型的数值计算方法

已知月降水量P(t)，月蒸发皿观测量EP(t)，则流域月实际蒸散发量E(t)可采用公式(3)来计算。扣除蒸散发之后的土壤含水量为S(t-1)+P(t)-E(t)，其中S(t-1)为第t-1个月底，第t个月初的土壤含水量。然后再根据公式(5)来计算流域月出流量Q(t)：

Q(t)=[S(t-1)+P(t)-E(t)]×

tanh{[S(t-1)+P(t)-E(t)]/SC}

(8)

最后得到第t个月底，第(t+1)个月初的土壤含水量S(t)[7]：

S(t)=S(t-1)+P(t)-E(t)-Q(t)

(9)

2.2 模型率定和评价准则

模型率定是指在模型结构(或程序)已经选定条件下，通过对历史资料的模拟分析，由给定的输入(降雨量及蒸散发量)和输出(径流过程)来确定模型中的参数，以用于未来情景下的模拟预测。根据我国水情预报规范，选用下列2个指标来评定模型或洪水预报方案的优劣。径流总量相对误差为：

(10)

3 2参数月水量平衡模型在西藏尼洋河流域应用结果分析

基于尼洋河流域所在站点降雨蒸发以及径流数据，率定月水量平衡模型参数，构建适合尼洋河流域径流模拟效果的2参数月水量平衡模型，并加以验证。

3.1 数据选择

收集了林芝站点、巴河站点1979-2005年月径流、月蒸发量数据和月降水数据，本研究将1979-1998年作为模型的率定期，1999-2005年作为模型的检验期。参数率定采用自动优选和人工相结合的方法，使用确定性系数R2作为目标函数。1999-2005尼洋河流域特征参数见表1。

表1 尼洋河流域特征参数Tab.1 Characteristic parameters of Niyanghe basin

1999-2005年尼洋河年平均降水量为710.93 mm，月平均降水量为59.24 mm，且年内变化大，分配很不均匀，每年11-4月降水少为枯水季节，6-9月多为雨季；蒸发强度受太阳辐射、气温、湿度及风速等因素的影响，尼洋河流域地区湿度小，多风且风速较大，1999-2005年平均蒸发量为1 747.22 mm，月平均蒸发量为145.6 mm；尼洋河流域的自然地理、气候等要素影响着河流径流的形成，1999-2005年平均径流为151.81 亿m3，月平均蒸发量为12.65 亿m3。

3.2 模型率定

为了能够很好地模拟尼洋河流域实际径流深的模型参数，模型参数率定可以通过一段系列的月径流、降水、蒸发资料找出c，SC值。考虑水平衡方程的简单特性，自动率定模型参数基于Matlab代码编制，算法计算过程见图2。

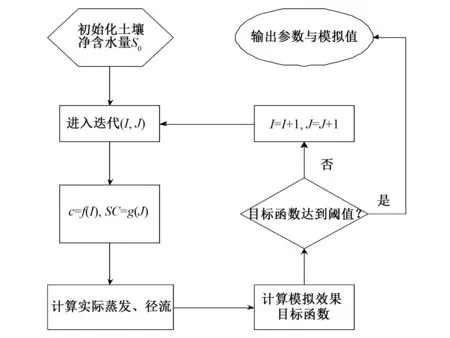
图2 2参数月水量平衡模型建立过程Fig.2 The flowchart of the calculation by two-factor monthly water balance model

通过尼洋河流域第1个月的径流深估算S0，模型的预热值采用c取1.0，SC取500计算获取。模型参数的率定取自1979年1月到1998年12月共324个月尼洋河流域站点的月径流、降水、蒸发数据，其中Nash指数值最高的c、SC值可采用自动率定参数小模块自动寻找，同时，另外2个模型效率指数RE尽可能接近于0，最终找出适合尼洋河流域的模型参数c、SC。

3.3 模拟结果分析

下面对其模拟结果进行分析，采用模型效率系数R2(确定性系数)、水量平衡系数RE来评价模型模拟的精度，R2值越接近于1表明模型效率越高，RE值越接近于0表明模型模拟得越好。表2给出了2参数月水量平衡的模拟结果。

表2 尼洋河流域率定期和检验期的模拟结果 %

从表2中可以看出，2参数月水量平衡模型径流的模拟基本令人满意。率定期内径流过程确定性系数达到78.8%，年径流相对误差均值为10.5%，模拟精度较高；检验期内径流过程确定性系数均值达到74.0%，年径流相对误差15.8%。从指标的确定性系数和相对误差可以看出，模拟效果均较为理想，且与通常的水文模型模拟结果相同，率定期模拟效果要好于检验期。由此可见，2参数月水量平衡模型在资料较为稀缺的尼洋河流域具有良好的适应性，模拟结果基本能模拟反映尼洋河流域的降雨径流特性。图3和图4分别绘出了尼洋河流域率定期和检验期的模拟结果、实测月径流过程及比较。

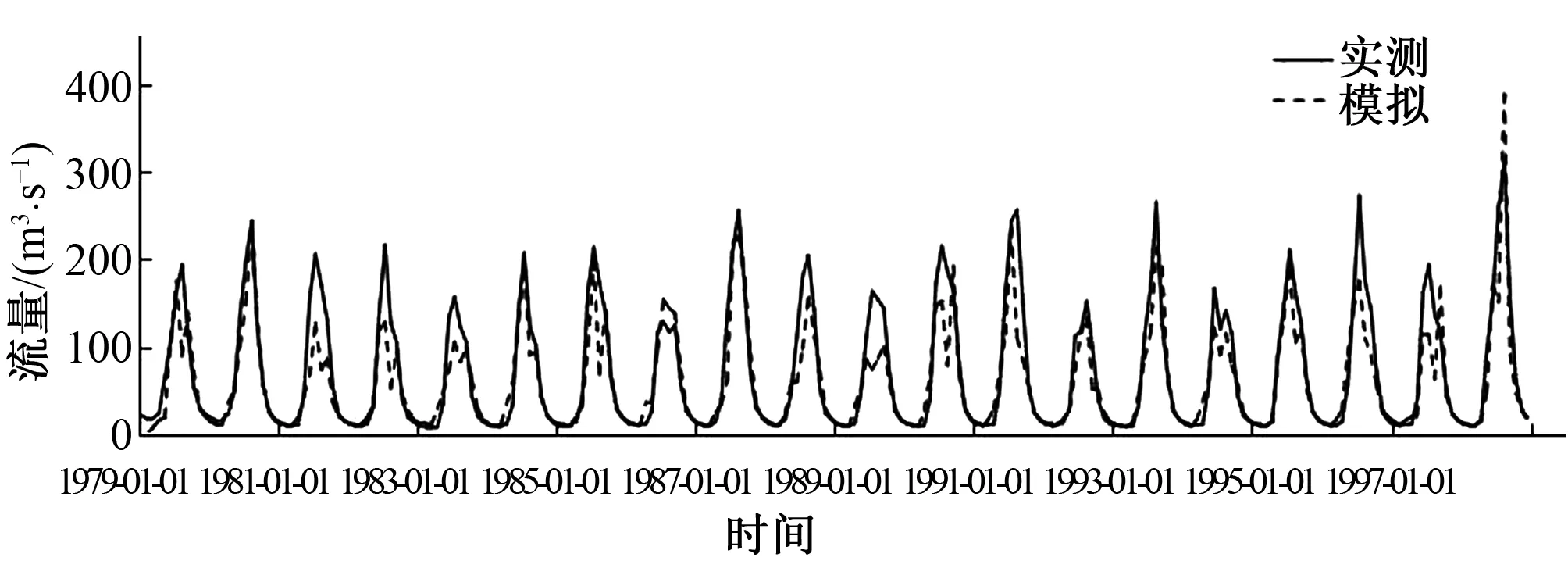
图3 率定期2参数月水量平衡模型模拟结果Fig.3 The simulation results for calibration period based on Two-factor monthly water balance model

图4 检验期2参数月水量平衡模型模拟结果Fig.4 The simulation results for validation period based on Two-factor monthly water balance model

从图3、图4中可以看出，2参数月水量平衡模型整体展现了良好的效果。率定期中，2参数月水量平衡模型在枯水期模拟过程十分贴近实测序列，而在丰水期，模型较为精确的重现了率定期月洪峰流量，仅在1998年对洪峰有轻微高估，高估的主要原因可能为98年洪涝灾害受到了明显的人为控制(包括水库等调蓄措施)。而在检验期，虽然模拟效果较率定期有所下降，仅在2005年的洪峰峰值有所低估，众所周知2005年发生了重旱，人为的补水可能是实测径流较高的主要原因。从整体模拟结果来看，尤其在资料稀缺的情况下，2参数月水量平衡模型可以较好地模拟流量过程。

4 结 语

相对于其他月水量平衡模型，本文采用结构相对简单、参数较少、对资料要求不高的2参数月水量平衡模型，结合尼洋河区域的水文资料，将1979-1998年作为模型的率定期，1999-2005年作为模型的检验期，得出了尼洋河流域率定期和检验期的模拟结果。

(1)2参数月水量平衡模型径流的模拟基本令人满意，模型在尼洋河流域具有良好的适应性，基本能模拟反映尼洋河流域的降雨径流特性。

(2)通过绘制出的尼洋河流域控制站率定期和检验期的模拟结果和实测径流过程，可以看出2参数月水量平衡模型可以较好地模拟流量过程。

另外通常枯水年的人类活动比较频繁，尤其在干旱地区，实测流量系列已受人类河道取水活动的干扰，而水文模型未考虑河道人为取水的影响，这也可能产生模型计算的误差，有待进一步研究。

□

[1] 李 帅, 熊立华,万 民.月水量平衡模型的比较研究[J].水文,2011,31(5):35-41.

[2] 陈瑜彬,杨文发.基于水量平衡的月水资源量长期预测方案探讨[J].人民长江,2013,44(11):9-13.

[3] 熊立华, 郭生练, 付小平, 等. 两参数月水量平衡模型的研制和应用[J]. 水科学进展, 1996,7(Z):80-86.

[4] 熊立华, 郭生练. 分布式流域水文模型[M]. 北京：中国水利水电出版社, 2004.

[5] Xiong Lihua, Guo Shenglian. A two-parameter monthly water balance model and its application[J]. Hydrol,1999,216:315-347.

[6] Morton F I. Operational estimates of areal evapotranspiration and their significance to the science and practice [J]. Journal of Hydrology, 1983,66:1-76.

[7] 詹道江.工程水文学[M]. 北京：中国水利水电出版社,2000.