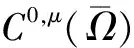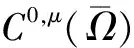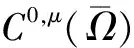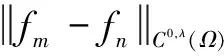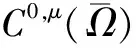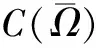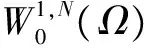Holder连续函数空间的插值空间的不等式
2018-03-20邢家省杨义川
邢家省, 杨义川
(1.北京航空航天大学数学与系统科学学院, 北京100191;2.数学、信息与行为教育部重点实验室, 北京100191)
引言
Holder连续函数空间是一类重要的函数空间[1-10],在偏微分方程[1-8]和泛函分析[9-21]的研究中得到广泛使用。Holder连续函数空间的完备性[1-8],嵌入的空间和紧嵌入的空间都得到充分的研究[1-10]。
Holder连续函数空间的嵌入空间和紧嵌入的空间,在文献[1-8]都是分别进行的,没有形成统一的理论方法。本文在文献[1-8]的基础上建立了Holder连续函数空间的插值空间不等式这一结果,并将这个结果应用于Holder连续函数空间的嵌入的空间和紧嵌入的空间,对分散的经典结果给予系统的明确改造,表现学术发展,推进学术认识。
1 Holder连续函数空间
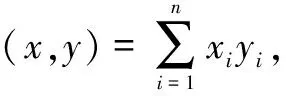
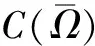
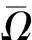
CB(Ω)是由定义在Ω上的有界连续函数全体组成。类似地可以定义
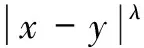
∀x,y∈Ω,0≤|α|≤m
这里K是常数,它可以依赖于函数
中元素f的范数由等式
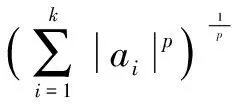
证明设
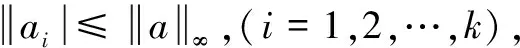
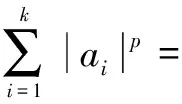
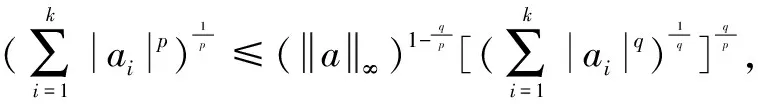
定理2设0 (1)对任意实数x≥y≥0,成立xp-yp≤(x-y)p; (2)对任意实数u,v,成立 |f(x)-f(y)|=|(|x-x0|λ-|y-x0|λ)|≤ 显然 显然,对每一x∈Ω,有 |f(x)|≤|f(x)-fN+1(x)|+|fN+1(x)|≤ 可知,f(x)在Ω上有界;再由fN+1(x)在Ω上一致连续,对上述ε>0,存在δ>0,当x,y∈Ω且|x-y|<δ时,成立|fN+1(x)-fN+1(y)|<ε。于是 |f(x)-f(y)|≤|f(x)-fN+1(x)|+ |fN+1(x)-fN+1(y)|+|f(y)-fN+1(y)|<3ε 定理3的结果,在文献[1-8]都有涉及,但给出证明表述的仅在文献[6]中出现。 ∀x,y∈Ω,x≠y,n∈N* 令n→∞,取极限,得 中,令m→∞,取极限,得 |f(x)-fn(x)|≤ε ∀x,y∈Ω,x≠y 证明[1-8]由不等式 ∀x,y∈Ω,x≠y 得 故成立 定理10的结果表述在文献[1-8] 不是明确单独出现的,尽管在文献[1-8]中的定理证明过程中出现了这种估计不等式,但都没有被认识到它的独立表述结果意义。 定理11[2,4]设Ω是Rn中的开集,0<λ<μ≤1,则有 证明[2,4]设 显然 得 A1A2+B1B2≤ 定理11仅出现在文献[2,4]中,虽然文献[2]出现很早,但没有充分认识到定理11的深刻有效性,没有利用定理11去改进相关结果的证明。这也说明了定理10不曾在文献[1,3,5-8]出现的原因。 证明利用定理10或定理11的结果,即可得到。 定理12的结果在文献[1-8]中都是给出相同的原始证明过程,这些过程不能导致定理10和定理11的发现。 定理13结果的证明,在文献[1-8]中有,但都没有意识到从中可以单独提炼出定理10或定理11的结果。在文献[2,4]中出现定理11,但也没有认识到可以用来证明定理12和定理13。这里给出的明确认识改造过程,建立知识捷径道路,推进学术认识发展。 [1] 李立康,郭毓騊.索伯列夫空间引论[M].上海:上海科学技术出版社,1981. [2] Adams R A,著.索伯列夫空间[M].叶其孝,王耀东,应隆安,等.译.北京:人民教育出版社,1983. [3] Gilbarg D,Trudinger N S.Elliptic Partial Differential Equations of Second Order[M].北京:世界图书出版公司北京公司,2001. [4] Adams R.A,Fournier J F.Sobolev Spaces[M].北京:世界图书出版公司北京公司,2009. [5] 郭柏灵.粘性消去法和差分格式的粘性[M].北京:科学出版社,1993. [6] 陈国旺.索伯列夫空间导论[M].北京:科学出版社,2013. [7] 王元明,徐君祥.索伯列夫空间讲义[M].南京:东南大学出版社,2000. [8] 陆文端.微分方程中的变分方法[M].北京:科学出版社,2003. [9] 邢家省,张愿章,崔玉英.一维区域上的Sobolev空间的嵌入定理[J].河南科学,2009,27(4):379-383. [11] 邢家省,杨义川,王拥军.函数列的广义积分的极限定理及其应用[J].吉首大学学报:自然科学版,2016,37(6):1-9. [12] 邢家省,杨义川,王拥军.函数列的黎曼积分的极限定理及其应用[J].四川理工学院学报:自然科学版,2017,30(3):73-78. [13] 郭金海.奥斯古德与函数论在中国的传播[J].中国科技史杂志,2014,35(1):1-15. [14] 邢家省,杨义川.函数列一致收敛的奥斯古德定理[J].四川理工学院学报:自然科学版,2017,30(6):83-88. [15] 李良树,周振荣.度量测度空间上的Holder连续函数的积分特征[J].华中师范大学学报:自然科学版,2012,46(4):385-388. [16] 巴娜,郑列.热传导方程解的部分Schauder估计[J].数学物理学报:A辑,2017,37(2):307-312. [17] 陆海霞.一类奇异弹性梁方程正解的存在性[J].应用数学,2016,29(3):665-671. [18] 吴秀兰,李仲庆,高文杰.一类具正初始能量和变指数源渗流方程解的爆破及爆破时间下界估计[J].应用数学学报,2017,40(3):400-408. [19] 王见勇.具有β-中点性质的非β-凸集(0<β<1)[J].数学的实践与识,2016,46(11):267-271. [20] 贾超华,冯德兴.分布阻尼下非线性梁光滑解的存在性[J].数学物理学报,2011,31(2):273-288. [22] 定光桂.等距线性延拓问题[J].中国科学:数学,2015,45(1):1-8.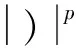
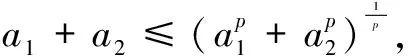
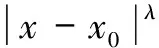
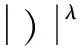

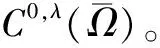
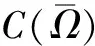
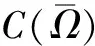
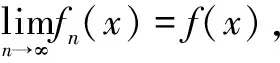
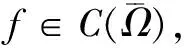
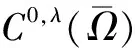
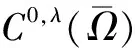
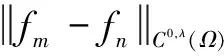
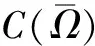
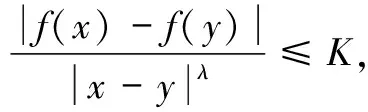
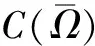
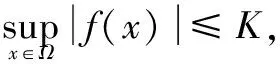
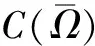
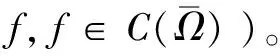
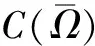
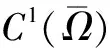
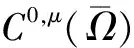
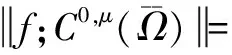
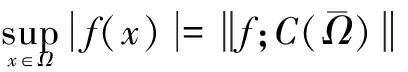
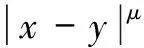
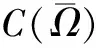
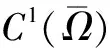
4 Holder连续函数空间的插值空间不等式
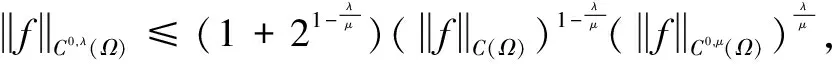
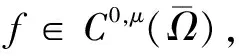
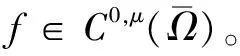
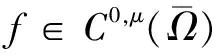
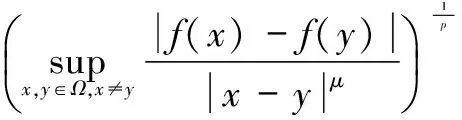
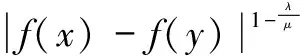
5 Holder连续函数空间的嵌入和紧嵌入的证明