基于主成分回归模型的泸州市物流需求影响分析

毕欢， 付宇， 陈一君， 韩兵， 王俊翔

(四川理工学院管理学院， 四川自贡643000)

引言

物流需求预测能为政府部门制定物流产业发展政策、建设物流基础设施以及为相关行业做出合理经济决策提供可靠的理论依据。伴随我国物流业的迅速发展，有关部门和企业对物流需求统计数据的需求越来越迫切，同时物流需求在社会经济中的重要作用也日益凸显。

在2014年国务院印发的《物流业发展中长期规划(2014-2020年)》文件中，不仅明确指出物流业在国民经济发展中的基础性作用和战略性地位，还凸显出物流需求研究的重要意义。泸州市地处四川省南部，是四川出海的南通道，也是长江上游重要的港口，在四川省物流发展大格局中占据着重要的战略地位。按照泸州市在国家长江经济带、“一带一路”、成渝经济区等战略布局中的功能定位，结合泸州市物流业所处的阶段及特点，进行泸州市物流业需求因素研究分析是十分必要的。本文以泸州市为研究对象，用新的研究思路，通过构建排序指标模型和主成分回归模型，解析各影响因素对物流需求的边际作用，旨为泸州市物流业发展提出合理化建议。

1 国内外研究现状

国内外学者对物流需求的研究主要体现在以下3个方面：

(1)在研究方法上，部分学者利用物流需求历史数据为指标进行物流需求预测[1-2]。何国华通过构建灰色GM(1,1)预测模型研究东北三省物流需求规模，并在预测中将该方法同平均增长率法和回归分析法进行综合比较，得出灰色预测法在区域物流需求的中短期预测中有较高的精确度[3]。ARIMA(自回归积分滑动平均模型)擅长处理具有自回归特性的时间序列数据，基于此，黄振等构建自回归移动平均模型对湖南省物流需求进行预测分析[4]。汤兆平等针对A、B两省铁路货运量占全国比重逐年减少现象，采用ARIMA模型对两省物流需求进行预测，并为两省制定相应货物运输营销策略提供参考依据[5]。选用单因素构建模型预测物流需求，虽然能得出较高精度的结果，但物流需求作为社会经济活动产生的一种派生需求，这种预测模型无法体现社会经济活动对物流业发展的联动作用[6]。

另一方面，部分学者基于物流与经济发展的不可分割特性，利用物流需求影响因素构建模型从而预测物流需求。后锐等构建MLP(多层神经网络)模型，揭示了物流需求与经济之间的内在非线性关系，并通过实证分析验证模型具有较高的精确度，能为物流需求预测方法提供新思路[7]。陈黎在对影响物流需求变动因素分析和最终指标选取的基础上，构建组合预测模型，对湖北省物流需求进行预测拟合[8]。黄虎等基于支持向量回归机方法，建立“影响因素-物流需求”支持向量机预测模型研究预测区域物流需求问题[9]。多因素物流需求分析的结果能解析出各因素对物流需求的影响程度，在实践中更具有指导意义。

(2)在物流量化指标选取上，综合考虑数据的合理性和可获得性，学者们一般选用货运量或货物周转量表征物流需求[10-11]。用定性分析法确定货运量与货物周转量哪个更能反映物流需求外，可参考前人研究关联因素时指标选取的方法，采用灰色关联分析与相关系数分析相结合的思路，建立排序指标模型，确定最终物流需求量化指标[12]。

(3)在物流影响因素的选取上，曾鸣等选取了国内生产总值、财政收入等36个与区域物流需求密切相关的影响因素，并采用互信息技术对其进行降维处理[13]。许沛沛等从区域经济规模、产业结构、经济空间布局及区域行业因素四个方面分析，采用了本地生产总值、固定资产投资总额、第一产业增加值等10个指标作为物流需求预测的影响因子[14]。除考虑影响物流需求的一般因素外，越来越多的学者考虑到所研究对象的地理位置、主导产业等因素，有针对性地完善该指标体系。黄虎等在传统的影响因素选取标准基础上，结合上海市经济特性，将区域外贸总额并入影响因素指标体系[15]。李国祥等结合广东、上海、广西三个地区物流业实际运营情况，对部分指标进行细化，构建区域物流需求的影响因素指标体系[16]。

综合前人研究成果，本文在其研究基础上，综合灰色关联分析法和相关系数分析法，优选出物流需求量化指标。在实证分析中，本文基于泸州市发展特性和物流需求量化指标，构建合理指标体系。再通过建立主成分回归模型，对物流需求进行预测，并解析影响泸州市物流需求的关键因素。

2 排序指标模型

2.1 灰色关联分析

灰色关联分析法是一种定量描述变量间动态变化相似度的方法，它是通过计算灰色关联度分析系统因素间的影响程度及各因素对系统主行为的贡献大小[17-21]。其基本思想是根据序列间曲线几何形状的相似程度判断序列间联系是否紧密，其曲线变化趋势越接近，相应序列间的关联度就越大，反之则越小。

(2)原始数列无量纲化处理。无量纲化处理包括初值化方法、均值化方法、区间化方法等。无量纲化后数列记为{x0(t)}和{xi(t)}。

(3)计算灰色关联系数。在t=k时，参照数列{x0(k)}与比较数列{xi(k)}的灰色关联系数为

(1)

其中，ρ为分辨系数，在(0,1)内取值，ρ越小，关联系数间差异越大，区分能力越强。通常ρ取值0.5。

(4)计算关联度。用比较数列与参考数列各个时期的关联系数的平均值定量反映两个数列的关联程度，计算公式为：

(2)

2.2 相关系数分析

相关系数是反映两个变量之间线性相关程度的数值。记参考序列为x0，比较序列为xi，比较序列与参照序列间的相关程度可表示为：

(3)

其中，r2i称为相关系数，该数取值范围为-1≤r2i≤1，r2i的绝对值越大，两个变量间的线性关系越强。

2.3 模型构建

基于灰色关联分析与相关系数分析，可以得到排序指标模型：

(4)

3 影响物流需求指标体系

本文在借鉴以往文献基础上，依据相关性、可操作性等原则，并结合泸州市实际情况，选取第一产业总产值、第二产业总产值、第三产业总产值、财政收入、固定资产投资总额、社会消费品零售总额、进出口总额等7个变量作为物流需求影响因子。

首先，三大产业产值不仅能反映一个地区的经济总量情况，同时也是产业结构的构成实体。一个区域的经济总量水平越高，其对物料的流通需求也会越高；各产业对物流需求功能、物流需求层次等要求不一，会使得产业结构的差异引起物流需求量的较大差异。其次，财政收入是国家实现公共基础设施建设、提供公共服务等带动经济活动的有力保证。固定资产投资的增加会促进社会经济的发展，从而带动社会物流需求。再次，因商业流通也是物流需求的一个重要组成部分，故将社会消费品零售总额纳入指标体系。最后，因为泸州市地处四川物流大通道的重要节点，拥有长江经济带上的一个内河港口—泸州港，其在对外贸易来往中产生的物流需求所占的比重不可忽视，故将进出口总额考虑进模型。

4 主成分回归分析模型

用多因素预测物流需求中，回归分析是常用的一种方法。由于在传统的多元线性回归模型中，多因素间往往存在着多重共线性。为消除多重共线性问题，常用方法有逐步回归方法、岭回归方法和主成分回归方法。

其中，逐步回归方法虽然能使得最后保留在模型中的变量之间的多重共线性不显著，但通过剔除不显著变量，可能会导致最终模型丢失部分重要信息；岭回归方法以放弃最小二乘法的无偏性、损失部分信息和降低精度为代价，其回归方程中系数的显著性优于普通回归模型，但在其回归参数的选择上，目前仍缺乏强有力的理论依据；而主成分回归方法通过降维，简化了模型结构、保留了原有变量中的大部分信息，它适用于一般的多重共线性，尤其是对变量间存在严重的多重共线性的情况[22]。

不少学者均采用主成分回归的思路进行问题分析，如彭佳红等以湖南省生态公益林需求量为研究对象，对所列15个指标进行主成分分析，最终确定2个主成分为自变量，带入回归模型进行需求量预测[23]。江期武等利用主成分分析消除分布滞后模型中变量间的多重共线性[24]。万红燕等基于主成分方法选择出3个主成分，并结合原来变量在主成分上的载荷系数对所选主成分归类命名，最后将其作为评价指标进行回归分析[25]。牛京考在对铁矿石需求影响的单因素分析基础上，通过主成分分析方法确定出4个主成分，并对其进行回归分析[26]。国外学者Hachicha将主成分分析方法用于选取相关相似矩阵中的特征值及特征向量，在此基础上，通过二维散点表示数据信息，最终还原出四个主要的机器分类情况[27]。Kasban通过实验分析，证明了基于主成分分析的分离算法相对于其他分离算法的优越性[28]。

4.1 主成分分析计算步骤

4.1.1原始数据标准化

(5)

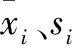
4.1.2计算相关系数矩阵

式中，rij表示变量xi与xj之间相关系数，m为样本量个数，n为影响因素的个数。相关系数计算公式同式(3)。

4.1.3计算特征值与特征向量

(1)计算特征值。解特征方程|λI-R|=0，常用雅可比法(Jacobi)，计算出各影响因素特征值λi(i=1,2,…n)，并按大小顺序对其排列，λ1≥λ2≥…≥λn≥0。

(2)计算特征向量。分别求出对应于特征值λi的特征向量ei(i=1,2,…n)，要求ei=1。

4.1.4计算主成分贡献率及累计贡献率

主成分Zi贡献率：

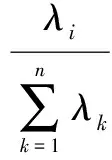
累计贡献率：

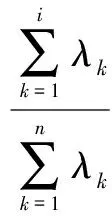
一般取累计贡献率达到85%～95%的特征值λ1，λ2，…,λn所对应的第1、第2、…、第p(p≤n)个主成分。

4.1.5计算主成分载荷矩阵

对前q个主成分的特征值求出其特征向量e1、e2、…、eq，计算各影响因素在各主成分上的载荷矩阵。主成分载荷矩阵计算公式为：

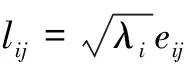
记x1,x2,…,xn为影响因子，zx1,zx2,…,zxn为影响因子标准化后变量，可依照式(5)变换得出。zk为影响因子的第k(k≤n)个主成分，表现形式为：

Zk=lk1zx1+lk2zx2+…+lknzxn

(6)

4.2 主成分回归模型

设物流需求量为y，物流需求影响因素为xi,i=1,2,…n。选取累计贡献率首次超过85%的前p个主成分记为Z1,Z2,…,Zp，建立y标准化后变量zy与所选的p个主成分之间的回归模型为：

zyt=a1Z1 t+a2Z2t+ … +apZpt+εt

(7)

对模型进行拟合优度检验、F值检验和回归系数的显著性检验—t检验等。

还原后得关于y的主成分回归模型为：

yt=b0+b1x1 t+b2x2t+ … +bpxpt+εt

(8)

由于主成分回归时均是对标准化后变量进行回归，常数项标准化后为零，故式(7)中不含常数项，ap为回归系数。在多元线性回归方程中bp为回归系数，代表对应自变量对因变量的边际作用。

5 实证分析

5.1 数据选取

考虑不同时期的政策导向作用导致的指标统计口径改变所带来的影响，选取泸州市2001年至2015年的各指标数据进行研究。

5.2 分析与泸州市经济关联较大的物流指标

(1)设泸州市地区生产总值为X0，货运量、货物周转量分别记为X1、X2。各指标数据见表1。

表1 泸州市部分统计数据

数据来源：《泸州统计年鉴》。

(2)依照灰色关联分析及相关系数分析计算步骤，可得：

参照数列为：

比较数列为：

灰色关联分析对原始数据初始化的几种方法中，初值化方法适用于较稳定的社会经济现象的无量纲化，本文通过观测各数列时间趋势图形特征后，决定对原始数据进行初值化处理。初值化后各数列形成矩阵：

(3)计算2个比较数列的r值及排序模型，结果见表2。

表2结果表明，泸州市货运量与地区生产总值的综合关联度结果r1>r2，可认为货运量在对物流需求量的代表性上优于货物周转量，故选用货运量作为物流需求量化指标。

5.3 主成分分析

泸州市2001年至2015年15年间货运量(y)，第一产业产值(x1)、第二产业产值(x2)、第三产业产值(x3)、财政收入(x4)、固定资产投资总额(x5)、社会消费品零售总额(x6)、进出口总额(x7)数据见表3。为使结论分析具有可比性，将原始变量量纲为万元及万美元的变量统一为以亿元为单位，其中进出口总额数值是通过相应年份人民币汇率换算得出。

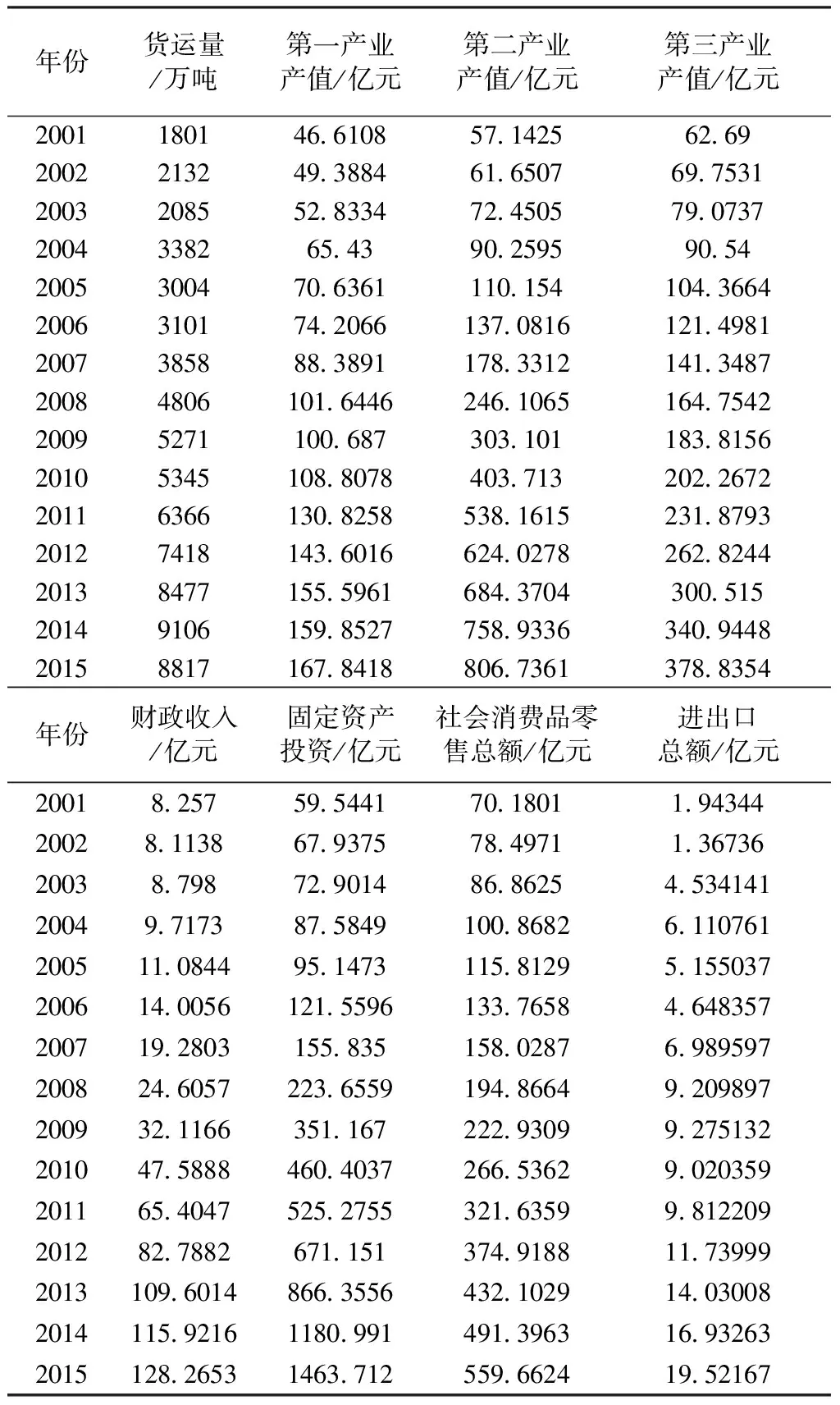
表3 泸州市货运量及7个指标统计数据

数据来源：《泸州统计年鉴》。

依照主成分分析步骤及表3数据，得x1,x2,…,x7间的相关系数矩阵

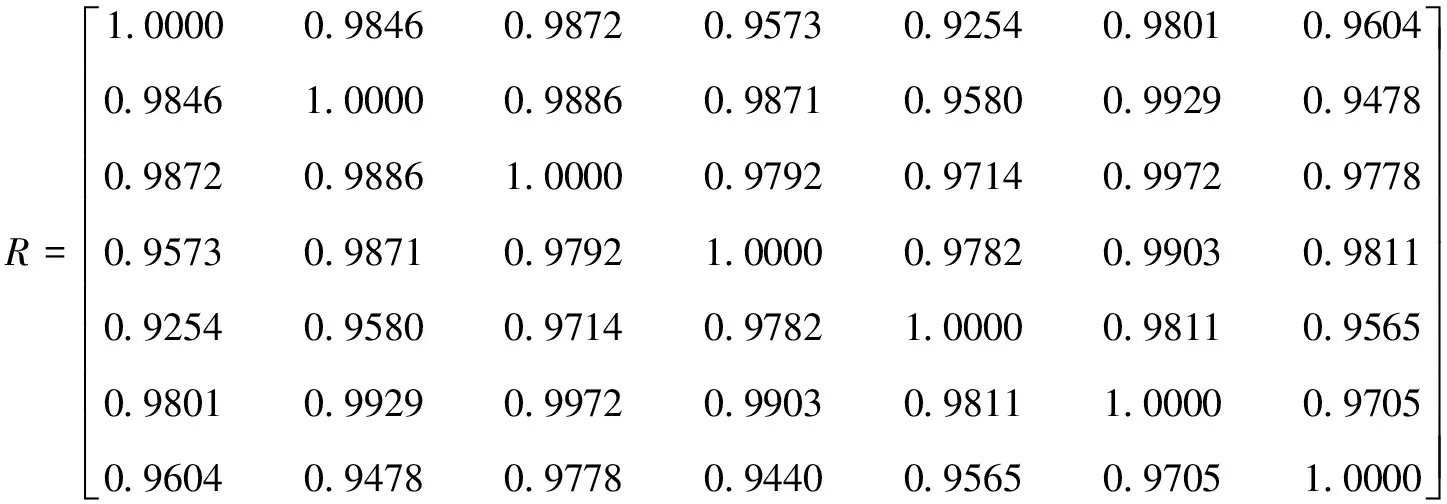
由上述相关矩阵还可知各影响因素间存在严重的多重共线性，考虑采用主成分分析方法。经过KMO(Kaiser-Meyer-Olkin)检验得KMO值为0.7963，依据常用的KMO度量标准可知，变量x1,x2,…,x7适合作主成分分析。7个主成分的特征值、贡献率及累计贡献率见表4。

通过表4主成分贡献率及累计贡献率结果，可知第一个主成分的累计贡献率已超过85%，故只需要求出第一个主成分Z1，计算变量x1,x2,…,x7在主成分Z1上的载荷矩阵。计算结果见表5。

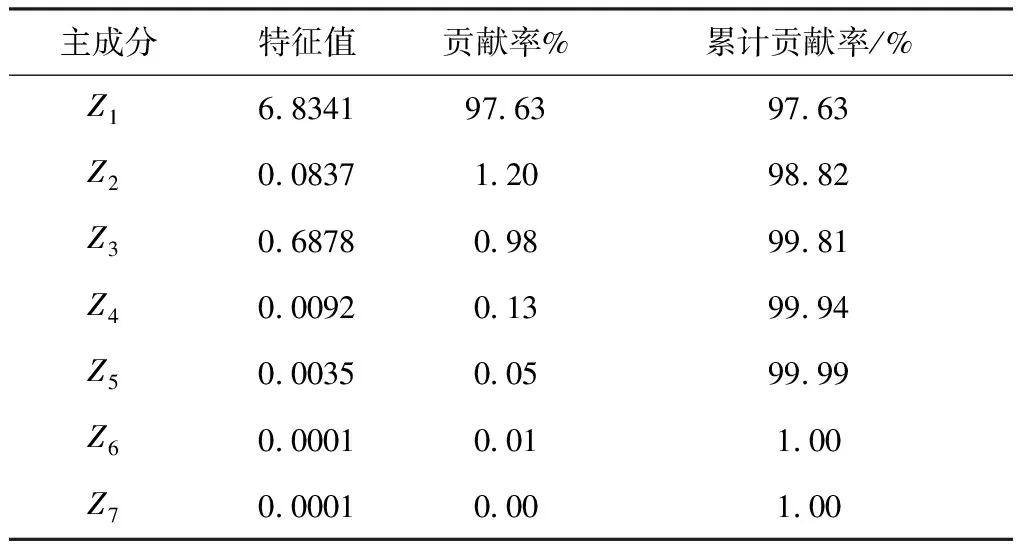
表4 主成分贡献率

表5 主成分载荷

依据(6)式有

Z1=0.376zx1+0.379zx2+0.382zx3+0.378zx4+

0.375zx5+0.382zx6+0.374zx7

(9)

5.4 主成分回归

构建货运量标准化后变量zy与Z1的主成分回归模型：

(10)

(1)对模型进行拟合优度检验、F值检验和回归系数的显著性检验—t检验，结果见表6。

表6 模型检验结果

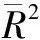
(2)异方差检验。结合怀特检验能够检验任何形式异方差的特点，采用该方法对模型进行异方差检验，结果见表7。

表7 怀特检验结果

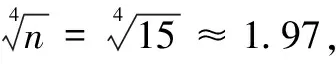
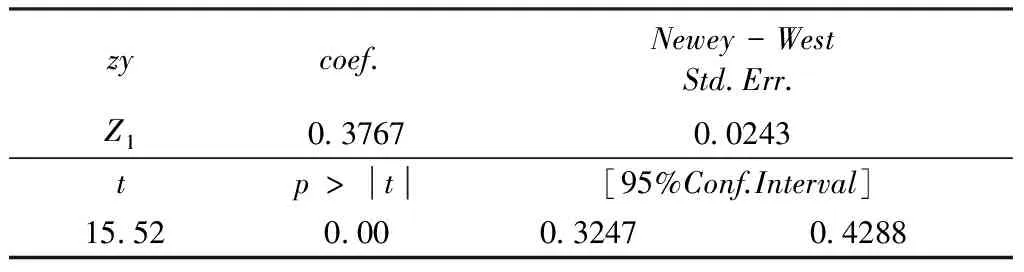
表8 检验结果

由表8可知，Newey-West标准误与OLS标准误相差很小(略大)，比较稳健。

(2)自相关检验。利用Stata分析软件进行BG检验，结果见表9。

表9 检验结果

表9显示，p值为0.5177大于0.05，于是接受原假设，认为不存在自相关。

经上述检验，得出不存在自相关。虽存在异方差，但使用异方差自相关稳健的标准误处理后发现结果较稳健，故可认为所建模型可信度较高。

结合(9)式和(10)式，得到y关于x1,x2,…,x7的方程为：

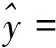
8.29x4+0.81x5+2.27x6+68.51x7

(11)

由式(11)知，回归系数bi>0,i=1,2,…,7均合理，三大产业产值、财政收入、固定资产投资总额、社会消费品零售总额、进出口总额对货运量均是正向影响作用。其中，进出口总额对货运量的边际作用最大，其余依次为第一产业产值>财政收入>第三产业产值>社会消费品零售总额>第二产业产值>固定资产投资总额。

5.5 预测结果

根据所建立的主成分回归模型对泸州市2006年至2015年货运量进行预测，货运量预测值结果见表10。

由表10可知，泸州市近10年货运量真实值与预测值之间的平均绝对误差百分比为5.10%，最低为0.03%。说明所建立的主成分回归模型是较为科学合理。

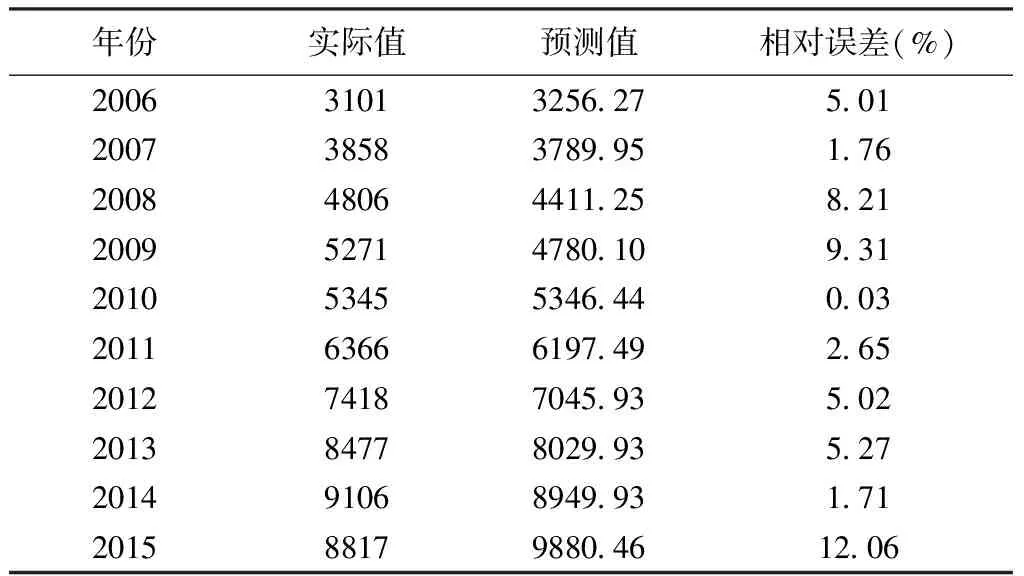
表10 预测值与实际值对比情况表

6 结论与建议

本文以泸州市为研究对象，围绕物流需求影响因素进行分析。首先综合灰色关联分析和相关系数分析方法建立排序指标模型，优选出货运量作为物流需求量化指标。其次，结合以往文献及泸州市自身特点，构建影响物流需求指标体系，对其进行主成分分析，将提取出的主成分与货运量进行线性回归，得到货运量与各影响因素的拟合方程。并对模型进行有效性等检验，检验结果表明模型可信度较高。最后，结合方程解析各影响因子对泸州市物流需求的影响并为泸州市物流业发展提供合理化建议如下：

(1)进出口总额对物流需求的边际影响远高于其他经济指标，但由于进出口总额占GDP比重较小，即对物流需求量的绝对影响程度不大。若泸州市产业发展对进出口产业的发展促进大，此时可相应加大物流业基础配套设施建设，进一步完善进出口岸的建设和规划，发挥其港口物流优势，提升进出口贸易对物流业的影响力。

(2)第一产业对物流的影响次之，说明虽然泸州市近15年第一产业占GDP比重逐年在下降，但其对物流业的需求的影响未减少，说明第一产业的发展仍需要较多的物流。因此，在将地区产业重心转至第二、第三产业同时，应合理优化产业结构，重视传统第一产业在社会经济发展中的基础性地位。

(3)地方财政收入是政府扩大物流基础设施建设的有力保证，政府应在正确处理各方面的物质利益的基础上，充分调动各方面的积极性，扩大地方财政收入以推动地区物流业的发展。

(4)第三产业产值、社会消费品零售总额、第二产业产值及固定资产投资总额对物流需求的影响较小，说明要达到通过发展第三产业来推动物流发展的目标，还需进一步努力。同时，也不能忽视社会消费品等因素对物流需求的增长影响。

[1] BAHRAM A,ARJUN C,KAMBIZ R.The Demand for US Air Transport Service：a Chaos and Nonlinearity Investigation[J].Transportation Research Part,2001,37(5):337-353.

[2] RODRIGO A,HANI S.Forecasting Freight Transportation Demand with the Space-time Multinomial Probity Model[J].Transportation Research Part,2000,34(5):403-418.

[3] 何国华.区域物流需求预测及灰色预测模型的应用[J].北京交通大学学报:社会科学版,2008(1):33-37.

[4] 黄振,张为,夏利平.基于ARIMA模型的湖南省物流需求预测研究[J].物流技术,2012,31(9):316-318.

[5] 汤兆平,孙剑萍,杜相,等.基于ARIMA模型的N铁路局管内物流需求预测研究[J].经济问题探索,2014(7):76-81.

[6] 伍星华.基于GSO-GNNM模型的区域物流需求预测[J].科技管理研究,2015,35(11):212-216.

[7] 后锐,张毕西.基于MLP神经网络的区域物流需求预测方法及其应用[J].系统工程理论与实践,2005,25(12):43-47.

[8] 陈黎.我国区域物流发展预测[J].统计与决策,2006(12):127-129.

[9] 黄虎,蒋葛夫,严余松,等.基于支持向量回归机的区域物流需求预测模型及其应用[J].计算机应用研究,2008,25(9):2738-2740.

[10] 曹萍,陈福集.GA-灰色神经网络的区域物流需求预测[J].北京理工大学学报:社会科学版,2012,14(1):66-70.

[11] 万励,李余琪,吴洁明.区域物流需求预测的应用研究[J].微电子学与计算机,2011,28(9):160-164.

[12] 谢炜,李军成,蒋亚萍,等.基于主成分回归模型的湖南省就业影响因素分析[J].数学的实践与认识,2015(20):35-43.

[13] 曾鸣,程文明,林磊.状态空间时间序列的区域物流需求预测研究[J].计算机工程与应用,2014(15):7-12.

[14] 许沛沛,何跃.基于自组织数据挖掘的区域物流需求预测[J].统计与决策,2011(6):58-59.

[15] 黄虎.区域物流需求预测模型研究[J].统计与决策,2008(17):62-64.

[16] 李国祥,夏国恩,高荣,等.基于属性约简的区域物流需求预测[J].计算机应用与软件,2013,30(11):60-63.

[17] 章文燕.基于灰色关联分析法的物流发展影响因素分析[J].统计与决策,2011(23):105-107.

[18] 毛巍,杜晶,兰恒友,等.大学生体质健康的灰色关联度综合评价与回归分析[J].四川理工学院学报:自然科学版,2014,27(4):96-100.

[19] 梅晓玲.基于灰色关联与投影算法的铁路货运量影响因素分析[J].四川理工学院学报:自然科学版,2015,28(5):85-88.

[20] 张荣艳,孙贵玲.全国区域经济发展水平的灰色关联聚类分析[J].四川理工学院学报:自然科学版,2016,29(2):95-100.

[21] 韩兵,陈一君,毕欢,等.基于因子分析和关联度分析的川南产业科技创新能力评价[J].四川理工学院学报:自然科学版,2017,30(4):87-95.

[22] 孔朝莉,李国徽,石明,等.基于GM(1,1)与主成分回归的海南GDP预测及其影响因素分析[J].数学的实践与认识,2016(17):66-80.

[23] 彭佳红,邹冬生,杨友.基于主成分非线性回归的湖南省生态公益林需求量预测模型[J].湖南农业大学学报:自然科学版,2015,41(6):691-694.

[24] 江期武,张浩敏.基于主成分回归的分布滞后模型及实证[J].统计与决策,2016(2):23-25.

[25] 万红燕,李仕兵.基于主成分回归分析的我国城镇居民收入差异的实证研究[J].预测,2009,28(1):77-80.

[26] 牛京考.基于主成分回归分析法预测中国铁矿石需求[J].北京科技大学学报,2011,33(10):1177-1181.

[27] KUMAR D S D,RAO P V.Analysis and design of principal component analysis and Hidden Markov Model for face recognition[J].Procedia Materials Science,2015,10(7):616625.

[28] KASBAN H,ARAFA H,ELARABY S M.Principle component analysis for radiotracer signal separation[J].Applied Radiation & Isotopes Including Data Instrumentation & Methods for Use in Agriculture Industry & Medicine,2016,112:20-26.