基于自适应变异二进制粒子群算法的WSN区域覆盖问题研究

李雨江, 潘博

(岭南师范学院数学与统计学院， 广东湛江524048)

引言

无线传感器网络节点的部署一般采用定点布置或随机布撒等形式[1]。随机布撒时，为保证监测区域的全覆盖，往往会在监测区域内部署大量传感器节点，当这些节点都工作时，就会产生大量的冗余节点，消耗大量能量[2-4]。研究表明，无线传感器网络中节点通信模块的能量开销占总能耗的90%以上，而通信模块处于发送、接收、空闲和休眠状态的功耗比为2000∶400∶400∶1[5]，因此，在不影响覆盖度和连通性的前提下，应尽可能多地使节点进入休眠状态以降低能耗。本文在区域覆盖理论的基础上，运用二进制粒子群优化算法(Binary Particle Swarm Optimization，BPSO)对无线传感器网络全覆盖问题进行优化，并针对算法所存在的不能收敛于全局最优解、局部搜索能力差[6]等缺点，借鉴遗传算法中的变异思想，在BPSO算法中引入变异操作，保证使用最少节点实现区域最大覆盖和连通。

1 相关研究

无线传感器网络覆盖控制的目的是在保证网络连通覆盖条件下，使处于活动状态的节点数最小[7]，在这方面人们做了大量研究。Tian[8]提出了基于扇区覆盖的DITIAN算法，算法通过扇形来计算邻居节点对1个节点的覆盖问题，由于该算法忽略了二倍探测半径之内的其他节点，导致漏判了部分冗余节点。文献[9]提出了覆盖配置协议(Coverage Configuration Protocol,CCP)算法，该算法依据交叉覆盖原理判断冗余节点，算法准确度较高，但计算复杂度较高。LIU等[10]提出了基于虚拟正方形网格的覆盖算法(Virtual Square Grid-based Coverage Algorithm，VSGCA)，该算法把每个节点的感知区域划分成小方格，然后计算每个邻居节点对这些小方格的覆盖，算法降低了计算复杂度，但休眠冗余节点数有所欠缺。谢佳华等[11]提出了基于改进粒子群的覆盖优化算法，算法融合了粒子的引力和碰撞作用，优化了节点布局，选出了更多的冗余节点。王爱民等[12]在文献[9]的基础上提出了一种节点循环替换的覆盖算法(FMWS)，算法分2个阶段，第一阶段运行CCP算法，第二阶段运行节点替换算法，用循环替代的方法，减少工作节点数量，但算法在部署节点较少的情况下效果不明显。

为进一步对随机分布的固定节点全覆盖问题进行研究，充分利用二进制粒子群算法全局寻优、并行搜索、分布式计算等特点，克服算法存在不足，提出一种基于自适应变异二进制粒子群的WSN区域覆盖优化算法，在保证监测区域全覆盖的条件下，最大限度的休眠冗余节点。

2 区域覆盖模型

2.1 节点覆盖模型

相关研究表明，如果一个节点的通信半径rc是其感知半径rs的二倍以上，则全覆盖即保证了全连通[13]，连通覆盖的问题可以简化为覆盖问题。假设在一个二维监测区间内，随机部署N个传感器节点，传感器节点集合为S={Si|i=1,2,…,N}，每个节点具有相同的性能。节点的感知半径rs为R，通讯半径rc为2R。节点Si的位置坐标为(xi,yi)，任意检测点O的坐标为(x0,y0)，节点Si与点O之间的距离为：

(1)

节点的感知区域是一个以节点坐标为圆心，半径为R的圆形封闭区域。传感器感知模型使用布尔(0-1)感知模型，则被节点检测到的概率模型为：

(2)

2.2 区域覆盖模型

将无线传感器网络监测区域划分成网格形式，其粒度(即相邻网格间的距离)由待求解问题的精度决定。评估网络覆盖性能时，将每个网格简化为像素点，分析各节点对该像素点的感知情况即可得到网络覆盖性能[14]。

设监测区域A内有m×n个像素点，用感知模型p(Si,o,R)衡量每个像素点是否被传感器节点覆盖。若像素点在节点集的覆盖范围内，则将像素点的覆盖状态标为1。节点集S的区域覆盖率Rarea(S)为节点S的覆盖像素点的总和与监测区域A的总像素点的比值，即：

(3)

3 二进制粒子群算法基本原理

粒子群优化算法最早由美国的J.Kennedy和R.C.Eberhart教授提出，广泛应用于函数优化、神经网络训练、模糊系统控制等领域。为使粒子群算法能解决离散组合优化问题，1997年，两人又设计出离散二进制粒子群算法[15]，扩展了粒子群算法的应用。

二进制粒子群算法(BPSO)的位置矢量是二进制空间，粒子在每一维上的取值只能是0或1，速度矢量仍然位于实数空间。BPSO速度矢量的更新公式为：

ViQ(k+1)=ωViQ(k)+c1γ1(phi-XiQ(k))

+c2γ2(pg-XiQ(k))

(4)

其中，c1、c2分别为粒子跟踪自己历史最优值和粒子跟踪群体最优值权重系数，通常设置为2；γ1、γ2是区间[0,1]内均匀分布的随机数；ω表示为惯性权值。位置矢量的更新公式为：

(5)

(6)

其中，g表示位置xir取1的概率

4 基于改进粒子群的WSN区域覆盖算法

4.1 改进粒子群算法

针对二进制粒子群算法不能收敛于全局最优解、局部搜索能力差的特点，基于遗传算法的变异思想，将遗传算法中的变异思想结合到粒子群算法中，使得基本粒子群算法能跳出局部最优，得到理想解[16]。对全局最优位置进行变异操作：

(8)

(9)

其中，stopf为最大迭代次数，mk为自适应变异概率因子，mk∈[0.001,0.05]，r表示为粒子二进制位数，则第i个粒子位置可以依据式(8)进行更新。

4.2 区域覆盖算法

通过节点位置变异改进后，得到改进的变异二进制粒子群算法(BPSO-G)。假设监测区域中有N个节点，则粒子的搜索空间就是N维二进制空间，粒子i的进化的第k代的位置矢量是Xi=(xi1,xi2,…,xio)，粒子每一维矢量的取值只能是0或1。

应用BPSO-G算法优化覆盖的目标是利用最少的节点实现监测区间最大覆盖，因此，定义适应度函数为：

maxf(X)=λ1f1(X)+λ1(1-f2(X))

(10)

(11)

(12)

其中，λ1、λ2为权重参数，满足λ1+λ2=1，|N|表示整个网络所有传感器节点数目，|N*|表示活动节点数目，函数f1表示网络覆盖率指标，即传感器节点覆盖面积与监测区域总面积比值，函数f2表示节点消耗率，即活动节点与网络区域总节点数的比值。

4.3 算法步骤

(1) 生成N个随机节点，节点将监测区域全覆盖，得到节点位置信息。

(2) 初始化整个种群位置X。X的行数为种群个数，每一行为一个粒子，每个粒子是N位的二进制数。

(3) 初始化速度，其最大速度为7，最小速度为-7。

(4) 根据覆盖公式求出粒子适应度值、每个粒子局部最优解和全局最优解。

(5) 初始化迭代次数k=1，程序进入主循环。

(6) 根据式(4)～(5)更新粒子速度、位置，并根据自适应变异函数(8)对位置变量以一定的概率重新初始化。

(7) 更新粒子适应度值、每个粒子局部最优解和全局最优解。

(8) 判断k是否等于最大迭代次数stopf，如果不等于stopf，则k=k+1，返回步骤(6)；如果等于stopf，则输出全局最优函数值及节点位置信息，算法结束。

5 仿真实验

5.1 算法仿真分析

对改进的区域覆盖算法进行仿真分析，设监测区域S= 50 m×50 m，节点在目标区域内随机分布，并保证全覆盖，节点数量N={100,200,300,400,500,600,700, 800,900}，传感器感知半径为10 m，通信半径为20 m，满足通信半径为探测半径二倍的关系。取仿真参数为ω=1，c1=c2=2，种群规模40，迭代次数500，适应度函数权重λ1=0.8，λ2=0.2，仿真计算结果均进行30次后取平均值。

监测区域节点经过BPSO-G算法覆盖控制前后分布情况分别如图1与图2所示。由图1可知，覆盖控制前，监测区域随机分布300个传感器节点，节点分布密集，冗余节点较多；算法控制后，监测区域活动节点较少，其余冗余节点被休眠，节省了网络区域能量，且能够保证网络的全覆盖。

图3表示经过BPSO-G算法覆盖控制后活动节点数随迭代次数变化的关系，由图3可知，算法能够很快收敛，得到满足区域全覆盖的最少节点数，且在较长的一段时间内活动节点数目连续不变。计算所得结果与文献[7]提出的perimeter pruning算法相近，印证了算法的准确性。

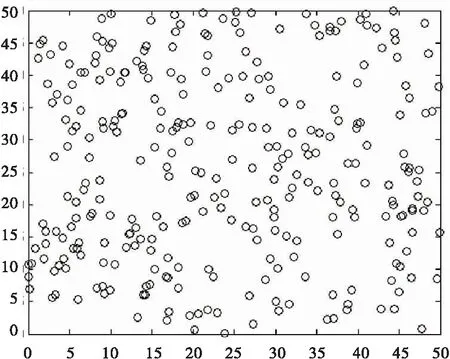
图1 随机分布300个节点情况

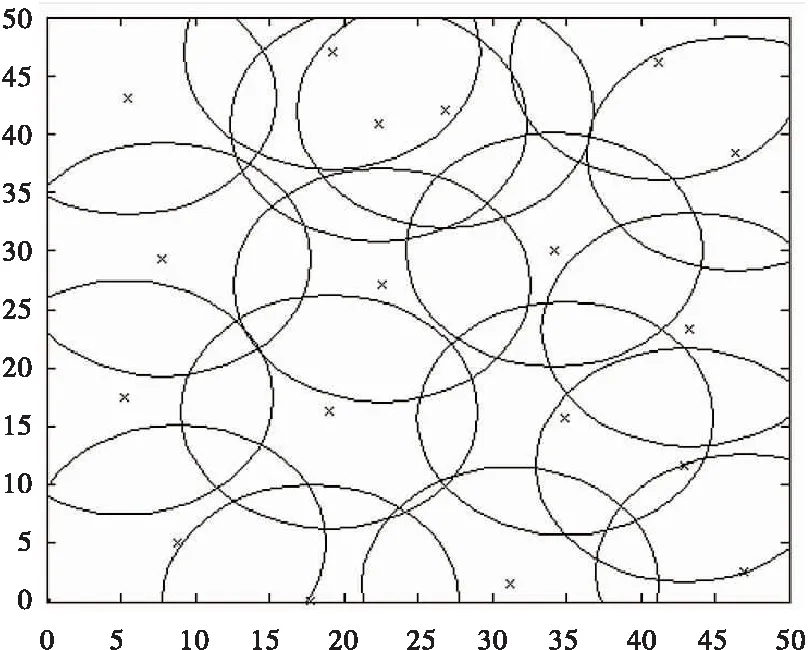
图2 覆盖控制后活动节点分布情况

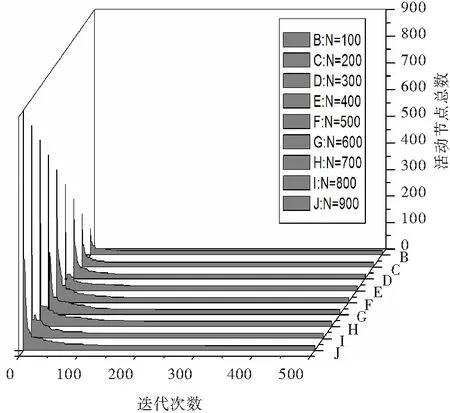
图3 活动节点数随迭代次数变化关系

5.2 与其他算法的比较

将本文BPSO-G算法与DITIAN算法、CCP算法、VSGCA算法以及FMWS算法进行比较。监测区域及传感器节点参数设置与文献[12]中相同。

本文算法与几种算法性能的对比如图4所示。由图4可知，本文BPSO-G算法的工作节点数比其他算法的都要少，DITIAN算法计算出的活动节点数最多，且随部署节点总数N的增加而近似呈现线性增长，其他算法得到的活动节点数保持在一定范围内，BPSO-G算法计算结果始终保持在[130，133]区间内，见表1，与CCP和FMWS算法相比，分别平均减少了约17%、8%。

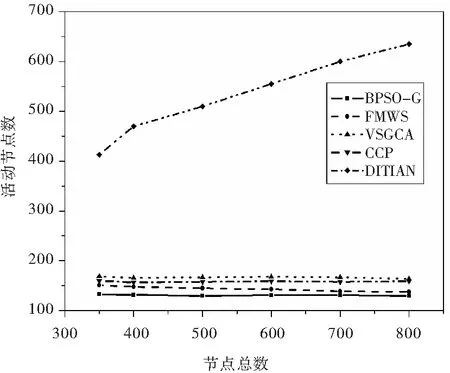
图4 节点总数与活动节点数目关系

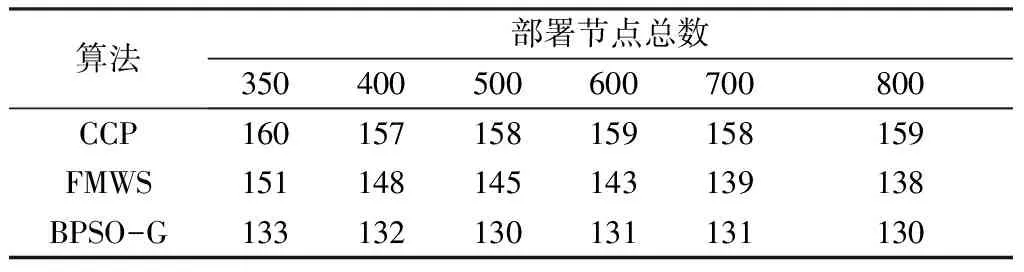
表1 几种算法所得活动节点数比较

6 结束语

本文在区域覆盖理论基础上，通过动态转换节点最优位置，给出了基于自适应变异二进制粒子群的无线传感器网络区域覆盖控制算法，用于求解全覆盖优化控制问题。仿真结果表明，本文提出的BPSO-G算法较DITIAN算法、CCP算法、VSGCA算法以及FMWS算法优越，与CCP和FMWS算法相比，算法所得活动节点数分别平均减少了约17%、8%。当监测区域面积一定，节点感知半径相同时，其活动节点数基本不随总节点数N的增加而增加，始终保持在一定区间内，且算法能够很快收敛于全局最优解，得到满足监测区域全覆盖条件下的最少数目和节点位置。

[1] 郭秀明,周国民,樊景超.无线传感器网络中节点部署算法研究综述[J].传感器与微系统,2015,34(7):14-16,25.

[2] ANJU S,PAL S R.Survey on coverage problems in wireless sensor networks[J].Wireless Personal Communications, 2015,80(4):1474-1500.

[3] KHAN J A,QURESHI H K,IQBAL A.Energymanagement in wireless sensor networks:a survey[J].Computers Electrical Engineering,2015,41:159-176.

[4] 王换招,孟凡治,李增智.高效节能的无线传感器网络覆盖保持协议[J].软件学报,2010,21(12):3124-3137.

[5] HILL J,SZEWCZYK R,WOO A,et al.System architecture directions for networked sensors[J].AcmSigops Operating Systems Review,2000,35(11):93-104.

[6] 刘建华,杨荣华,孙水华.离散二进制粒子群算法分析[J].南京大学学报:自然科学版,2011,47(5):504-514.

[7] 赵大胜.无线传感器网络广播与节点休眠算法中的节能覆盖问题研究[D].武汉:华中科技大学,2005.

[8] TIAN D,GEORGANAS N D.A coverage-preserving node scheduling scheme for large wireless sensor networks[C]//Proceedingof WSNA' 02 Proceedings of the 1st ACM international workshop on Wireless sensor networks and applications,Atlanta,Georgia,USA,September 28-28,2002:32-41.

[9] XING G L,WANG X R,ZHANG Y F,et al.Integratedcoverage and connectivity configuration for energy conservation in sensor networks[J].ACM Transations on Seneor Networks,2005,1(1):36-72.

[10] LIU Y H,SUO L X,SUN D Y,et al.Avirtual square grid-based coverage algorithm of redundant node for wireless sensor networks[J].Journal of Network and Computer Applications,2013,36(2):811-817.

[11] 谢佳华,刘军.无线网络通信覆盖优化仿真研究[J].计算机仿真,2015,32(6):271-275.

[12] 王爱民,刘永强,张婧,等.WSNs中一种寻找最小工作节点集的覆盖算法[J].西安电子科技大学学报,2016,43(4):141-146.

[13] ZHANG H H,HOU J C.Maintaining sensing coverage and connectivity in large sensor networks[J].Ad Hoc & Sensor Wireless Networks,2005,1(2):121-161.

[14] 李海华,范娟,陈莉.网格法在无线传感器网络部署中的应用[J].传感器与微系统,2012,31(3):150-152.

[15] KENNEDY J,EBERHART R.A discrete binary version of the particle swarm algorithm[C]//Proceeding of 1997 IEEE International Conference onSystems,Man,andCybernetics,Orlando,FL,USA,October 12-15,1997:4104-4109.

[16] MUHAMMAD I M,FEI M R,WANG L,et al.Adaptive mutation based probability binary PSO for control of ball mill pulverizing system[J].系统仿真学报,2011,23(8):1568-1574.