基于非局部理论的参数不确定纳米梁的非线性振动分析
2018-03-20刘延彬
刘延彬
(安徽理工大学力物院, 安徽淮南232001)
引言
随着纳米机电技术的发展,纳米尺度梁的力学特性引起了众多学者的关注。纳米梁的主要特点是小尺度效应突现[1],表面积的相对增大导致能量耗散机理显得更为复杂[2],动态响应出现明显的非线性特征[3]。因此,经典局部连续介质力学不再适用于对纳米梁的动态分析[1-4 ]。许多学者基于非局部理论对纳米梁的动态响应进行了广泛的研究[6-11]。非局部理论是 Eringen[12]在20世纪20年代提出,该理论认为求解域内的一点的应力状态不仅与该点的应变有关,而且与周围点的应变有关。自提出以来,非局部理论在物理和实际工程中获得良好的应用。
近年来,纳米梁的非线性动态响应的研究取得大量的成果。Peddieson等应用非局部理论研究了正弦载荷激励的双端简支纳米梁的振动问题[13]。Rahmani采用Timoshenko梁模型分析了功能梯度纳米梁的尺度效应[14]。Atabakhshian 基于非局部理论分析了耦合纳米梁的热-电耦合振动[15]。Eltaherc采用非局部理论分析了小尺度效应对功能梯度纳米梁的自由振动响应的影响[16]。Nazemnezhad 根据非局部理论建立了功能梯度纳米梁的非线性振动方程,分析了非线性振动的影响[17]。此外,许多学者采用非局部理论对纳米尺度梁进行大量的研究,取得了众多有益的结论[18-20]。
在以往的研究中,纳米梁的数学模型均是假定其参数为确定性参数。然而,外激励的不确定性、材料参数的不确定性、几何尺寸的不确定性等大量不确定因素的存在,必然导致纳米梁的参数是不确定的。受不确定参数的影响,如果仍采用确定性的理论和方法分析具有不确定参数的纳米梁的动力学特性,分析结果必然与实际结果有出入较大,故需要研究不确定参数对纳米梁的动力学特性的影响。
本文采用区间分析法及变分法研究具有不确定参数的纳米梁的非线性动力学响应。首先以基于非局部理论的 Euler-Bernoulli 梁为基础,建立区间变量纳米梁的非线性振动方程;其次采用变分法对参数不确定纳米的振动方程求解;然后由区间分析法给出响应的上下限;最后给出参数不确定纳米梁振动方程的数值求解方法,采用数值解验证解析分析的正确性。对于具有不确定参数的非线性系统的研究,本文所提出的分析方法具有重要的理论价值及工程意义。
1 基于区间变量的纳米梁力学模型
考虑图1 所示的两端为简支的纳米梁,其密度为ρ,弹性模量为E,横截面积为S,长度为l,结构阻尼系数为C,外激励的幅值为F,且外激励频率为ω。由于材料、加工误差及几何尺寸的不确定性,纳米梁的弹性模量E,长度l,结构阻尼系数C及外激励的幅值F为不确定参数,且它们处在一定的确定区间内。
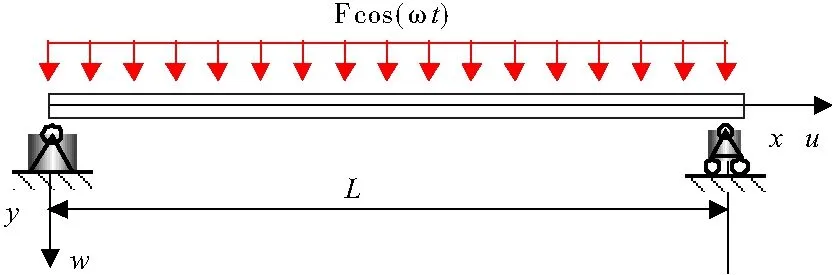
图1 纳米梁示意图
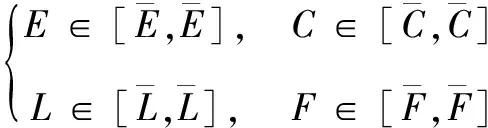
(1)
不确定参数的中位数为:
(2)
不确定参数偏离中位数的偏差为:
(3)
则不确定参数表示为区间变量为:
(4)
其中:
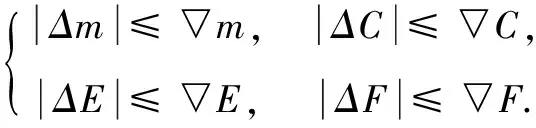
(5)
根据非局部理论[13],应力与应变的关系可以表示为:
(6)
其中,e0a为纳米梁小尺度效应的参数。对于纳米梁的大幅振动,轴向von Kármán非线性应变与位移的关系为[13]:
(7)
其中,u为轴向位移。对于Euler-Bernoulli 梁,轴向力为[13]:
(8)
弯矩为:
(9)
则纳米梁的动能T为:
(10)
纳米梁的势能为:
(11)
外载荷的功为:

(12)
由Hamilton原理可得区间变量的纳米梁振动方程:
(13)
边界条件为:
(14)
2 区间变量的纳米梁振动解析求解
根据 Galerkin 方法将两端简支的梁的横向振动的解函数写为
(15)
将方程(15)带入(13)可得:
(16)
其中:
(17)
方程(16)的一阶渐进解为:
q(t)=Acos(ωt+θ)
(18)
令:
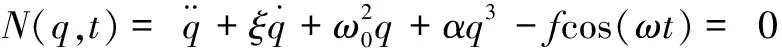
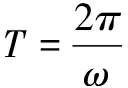
(19)
由变分法可得
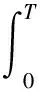
(20)
其中,δ为变分符号,由于
δq=cos(ωt+θ)δA-ωAsin(ωt+θ)δθ
(21)
则由方程(20)和(21)可得:
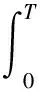
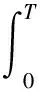
(22)
由于δA与δθ为独立变分,由方程(22)可得:
(23)
由方程组(23)可得:
(24)
由方程组(24)消去θ可得:
(25)
3 不确定动力响应的区间确定
由于A是参数E,c,l,F的函数,将其写为
A=A(E,c,l,F)
(26)
设
A0=A(E0,C0,L0,F0)
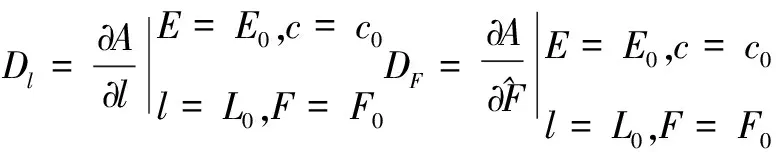
(27)
将A展开成Taylor 级数形式,保留一阶项:
A=A0+DEΔE+DcΔC+DlΔL+DFΔF
(28)
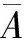
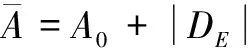
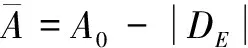
(29)
在式(29)中,各个区间变量的一阶偏导数未确定,故需确定区间变量的一阶偏导数。设:
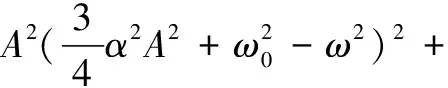
(ξω0ωA)2-f2
(30)
则方程(25)可以写为:
J(E,c,l,F,A)=0
(31)
对方程(31)的各个区间变量求偏导数可得:
(32)
从方程组(32)可以求得:
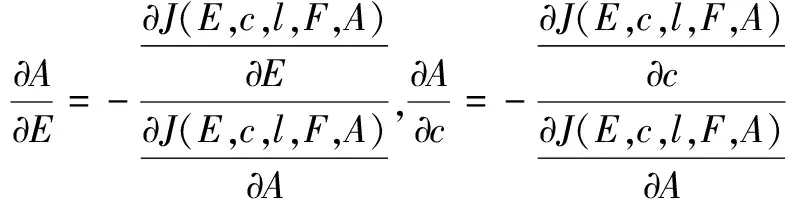
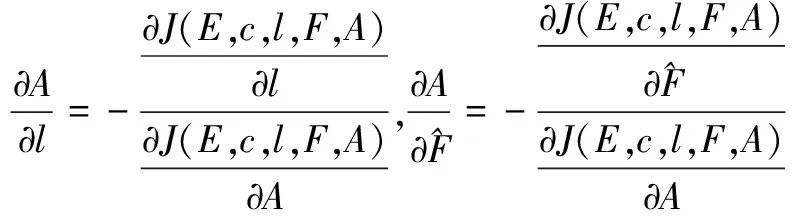
(33)
设:
(34)
将式(34)带入方程组 (33) ,则可以得到:
(35)
4 区间变量纳米梁的振动响应区间的数值求解格式
不确定响应q(t) 可以写为:
q=q(E,c,l,F,t)
(36)
设
q0=q(E0,c0,L0,F0,t)
(37)
将q展开成Taylor级数形式:
q=q0+GEΔE+GcΔc+GlΔL+GFΔF
(38)

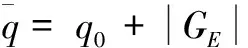
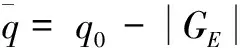
(39)
将方程 (16) 写为
f(F,l)cos(ωt)
(40)
则方程 (40)的一阶偏导数为:
(41)
将E0、C0、L0和F0带入方程(40)和方程(41)可得方程(42)。
f(F0,L0)cos(ωt)
(42)
5 振动响应区间的计算及分析
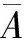
E=[E0-βE0,E0+βE0],c=[C0-βC0,C0+βC0]
l=[L0-βL0,k0-βL0],F=[F0-βF0,β+βF0]
(43)
计算参数见表1,参数不确定纳米梁的幅值与频率关系曲线如图2所示。

表1 参数表
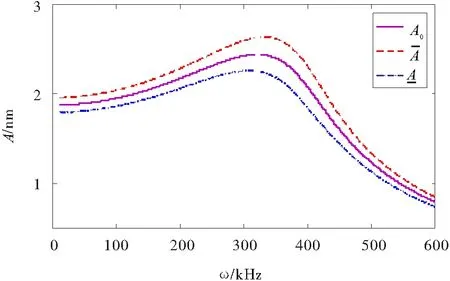
图2 主共振的幅频曲线
在方程(41)中,参数均为确定性的参数,其为常规的二阶非线性常微分方程,故可以进行求解。本文采用Runge-Kutta 法从方程(42)求解q0,GF,Gc,Gl及,GF,并与Monte Carlo 数值模拟[21]进行对比。当E=170 GPa;l=150 nm;F=0.5 N/nm; C=0.1 Pa/ nm,β=0.01时,基于区间分析的纳米梁的非线性振动的响应的时间历程图如图3所示,基于Monte Carlo 数值模拟的纳米梁的非线性振动的响应的时间历程图如图4所示,Monte Carlo 数值模拟的次数为500次。
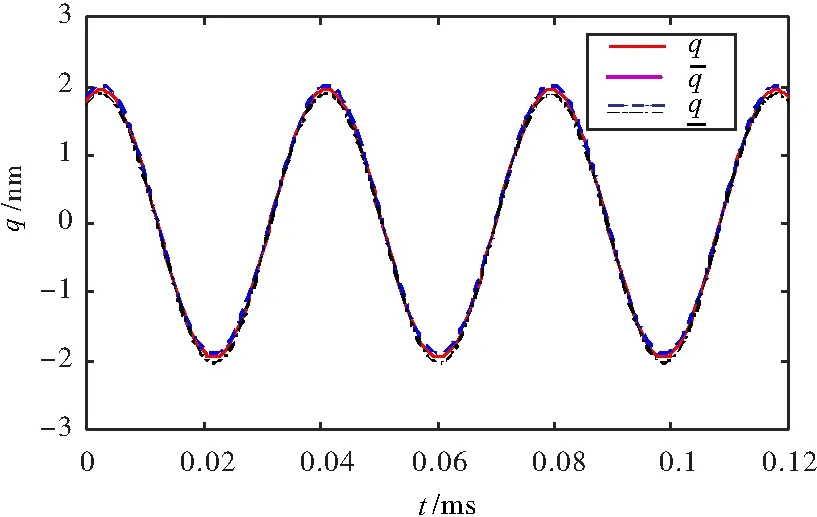
图3 纳米梁振动响应的时间历程图

图4 纳米梁振动响应的蒙特卡洛模拟图
在图4中,q0为均值,q1=q-3δ,q2=q+3δ,δ为标准差。由图3和图4可知,基于区间分析的纳米梁非线性振动响应与基于Monte Carlo 模拟计算的响应基本一致,说明区间分析方法可以很好的替代Monte Carlo数值模拟。区间分析与Monte Carlo 方法模拟的区间对比如图5所示。其中a=6δ,b=4δ,c为区间分析所计算的区间。由图5可知,区间分析的计算结果处于4δ与6δ之间,且接近于6δ,具有较好的置信度。图5说明区间分析结果与统计分析结果是一致的,具有良好的可信度,在具有不确定参数纳米梁的非线性振动响应分析中,区间分析方法可以作为统计分析的一种替代方法。
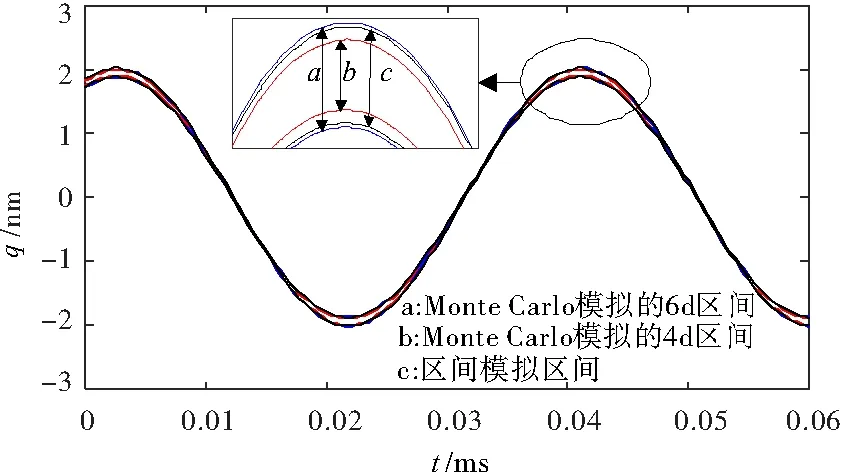
图5 区间对比图
基于区间分析的纳米梁的非线性振动的幅频曲线如图6所示。由图6可知,在共振带附近参数的不确定性对于系统响应的影响较大,不确定带宽的相对值为6.7%,随着外激励频率的增加,系统响应的不确定性逐渐减小。这与图2中的定性分析结果是一致的。
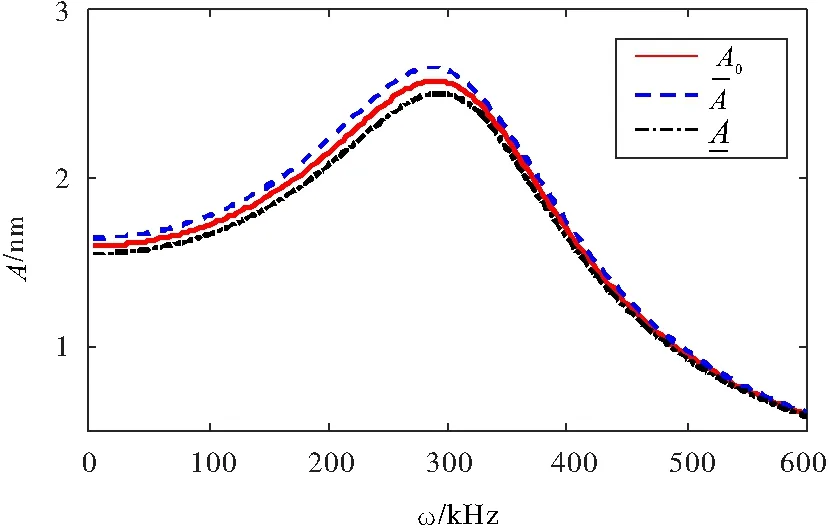
图6 纳米梁振动的幅频曲线
6 结论
本文采用区间分析法及变分法分析了参数不确定纳米梁的主共振响应,并且给出了数值求解参数不确定纳米梁的振动方程的方法,采用Monte Carlo 方法对本文推导的方法进行了验证。研究结果表明,不确定参数对参数纳米梁的主共振响应具有较大的影响,在实际问题分析中,不能忽略参数的不确定性。
[1] SOLTANREZAEE M,FARROKHABADI A,GHAZAVI M R.The influence of dispersion forces on the size-dependent pull-in instability of general cantilever nano-beams containing geometrical non-linearity[J].International Journal of Mechanical Sciences,2016,119:114-124.
[2] HOSSEINI-HASHEMI S,NAHASI,FAKHER M,et al.Surface effects on nonlinear free vibration of functionally graded nanobeams using nonlocal elasticity[J].Applied Mathematical Modelling,2013,38(14):35.
[3] NEJAD M Z,HADI A,RASTGOO A.Buckling analysis of arbitrary two-directional functionally graded Euler-Bernoulli nano-beams based on nonlocal elasticity theory[J].International Journal of Engineering Science,2016,103:1-10.
[4] LEE J W,LEE J Y.Free vibration analysis of functionally graded Bernoulli-Euler beams using an exact transfer matrix expression[J].International Journal of Mechanical Sciences,2017,122:1-17.
[5] YANG Y,LAM C C,KOU K P.Forced vibration analysis of functionally graded beams by the meshfree boundary-domain integral equation method[J].Engineering Analysis with Boundary Elements,2016,72:100-110.
[6] LI X,LI L,HU Y,et al.Bending,buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory[J].Composite Structures,2017,165:250-265.
[7] ROQUE C M C,MARTINS P A L S,FETTEORA A J M,et al.Differential evolution for free vibration optimization of functionally graded nano beams[J].Composite Structures,2016,156:29-34.
[8] NEJAD M Z,HADO A. Eringen’s non-local elasticity theory for bending analysis of bi-directional functionally graded Euler-Bernoulli nano-beams[J].International Journal of Engineering Science,2016,106:1-9.
[9] SHAAT M,ABDELKEFI A.Material structure and size effects on the nonlinear dynamics of electrostatically-actuated nano-beams[J].2016,89:11-17.
[10] SHAAT M,KHORSHIDI M A,ABDELKEFI A,et al.Modeling and Vibration Characteristics of Cracked Nano-Beams Made of Nanocrystalline Materials[J].International Journal of Mechanical Sciences,2016,s 115-116:574-585.
[11] NEJAD M Z,HADI A.Non-local analysis of free vibration of bi-directional functionally graded Euler-Bernoulli nano-beams[J].International Journal of Engineering Science,2016,105:1-11.
[12] ERINGEN A C,ERINGEN A C.Nonlocal polar elastic continua[J].International Journal of Engineering Science,1972,10(1):1-16.
[13] PEDDIESON J,BUCHANAN G R,MCNITT R P.Application of nonlocal continuum models to nanotechnology[J].International Journal of Engineering Science,2003,41(3-5):305-312.
[14] RAHMANI O,PEDRAM O.Analysis and modeling the size effect on vibration of functionally graded nanobeams based on nonlocal Timoshenko beam theory[J].International Journal of Engineering Science,2014,77(7):55-70.
[15] ATABAKHSHIAN V,SJPPSJTARO A,KARIMI M.Electro-thermal vibration of a smart coupled nanobeam system with an internal flow based on nonlocal elasticity theory[J].Physica B Condensed Matter,2015,456(3):375-382.
[16] ELTAHER M A,EMAM S A,MAHMOUD F F.Free vibration analysis of functionally graded size-dependent nanobeams[J].Applied Mathematics & Computation,2012,218(218):7406-7420.
[17] HOSSEINI-HASHEMI S,ZARE M,NAZEMNEZHAD R.An exact analytical approach for free vibration of Mindlin rectangular nano-plates via nonlocal elasticity[J].Composite Structures,2013,100(5):290-299.
[18] HOSSEINI-HASHEMI S,KERMAJANI M,Nazemnezhad R.An analytical study on the buckling and free vibration of rectangular nanoplates using nonlocal third-order shear deformation plate theory[J].European Journal of Mechanics-A/Solids,2015,51:29-43.
[19] ANSARI R,GHOLAMI R,ROUHI H.Size-dependent nonlinear forced vibration analysis of magneto-electro-thermo-elastic Timoshenko nanobeams based upon the nonlocal elasticity theory[J].Composite Structures,2015,126:216-226.
[20] MALEKZADEH P,SHOJAEE M.Surface and nonlocal effects on the nonlinear free vibration of non-uniform nanobeams[J].Composites Part B Engineering,2013,52(5):84-92.
[21] 张孝泽.蒙特卡罗模拟主方程的一般技巧[J].计算物理,1984,1(2):133-143.
